Стороны параллелограмма

1.

2.

Решить задачи
1) Стороны параллелограмма 10 см и
15 см, а одна из высот 6 см. Найти
длину второй высоты. Сколько
решений может иметь задача?
2) Стороны параллелограмма равны
10 см и 6 см, а угол между этими
сторонами 150°. Найти его площадь.

3.

4.

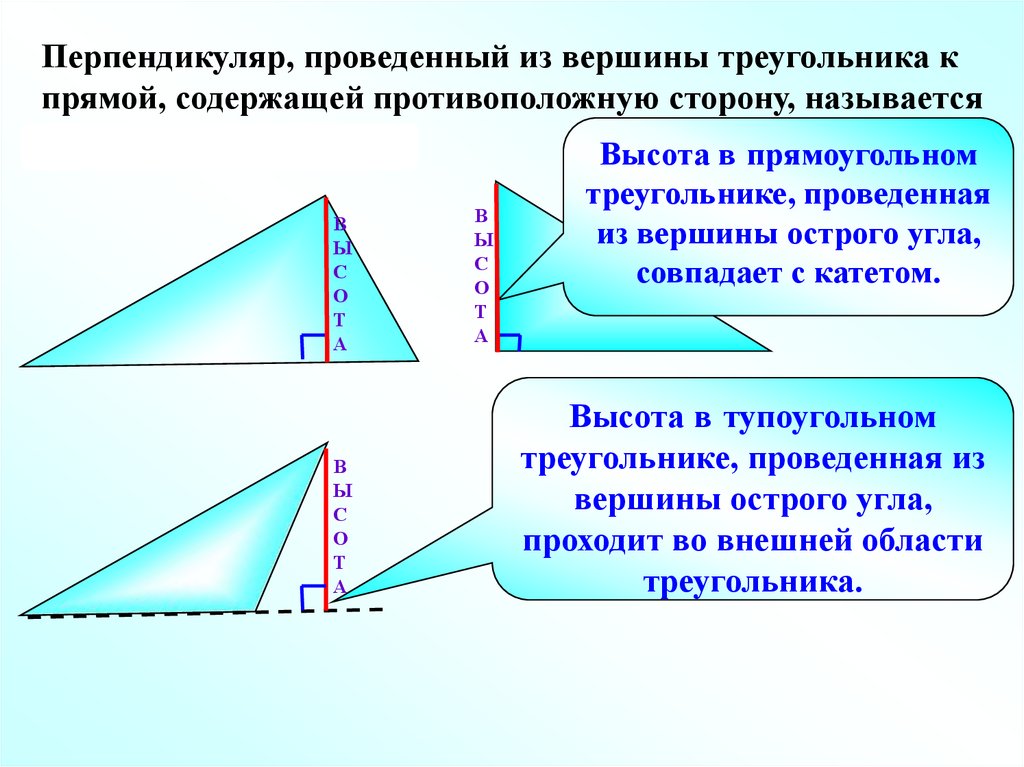
Перпендикуляр, проведенный из вершины треугольника к
прямой, содержащей противоположную сторону, называется
высотой треугольника.
Высота в прямоугольном
В
Ы
С
О
Т
А
В
Ы
С
О
Т
А
В
Ы
С
О
Т
А
треугольнике, проведенная
из вершины острого угла,
совпадает с катетом.
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.

5.

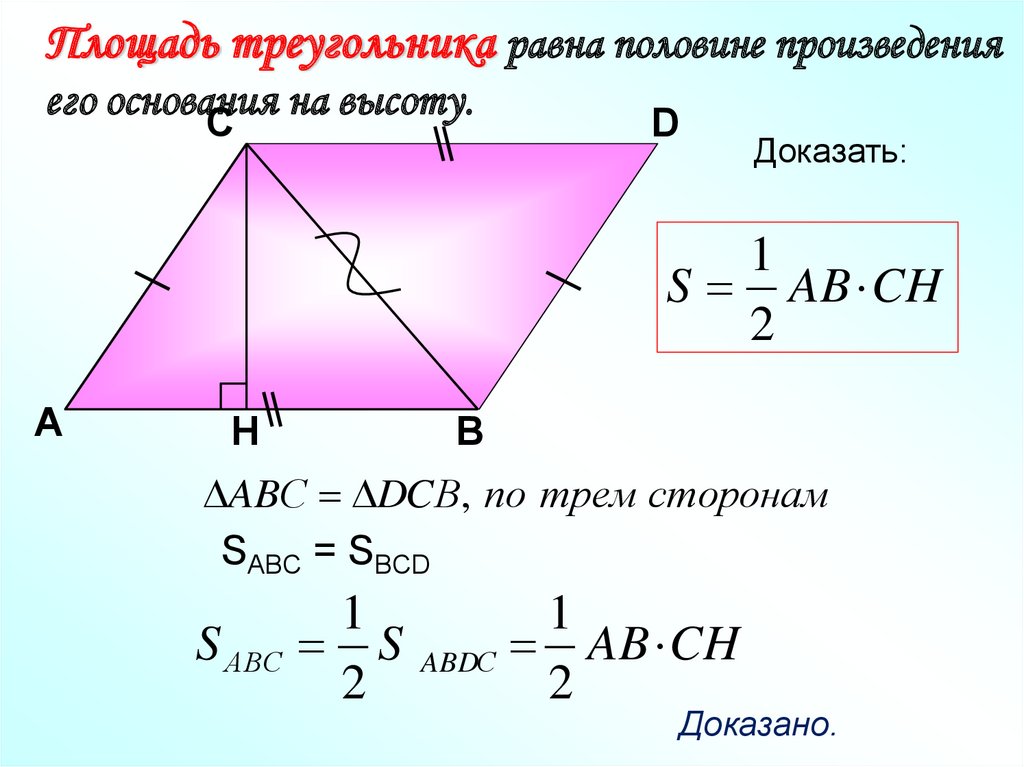
Площадь треугольника равна половине произведения
его основания
на
высоту.
С
D
Доказать:
1
S AB CH
2
А
В
H
ABС DCВ, по трем сторонам
SABC = SBCD
S АВС
1
S
2
1
AB CH
ABDС
2
Доказано.

6.

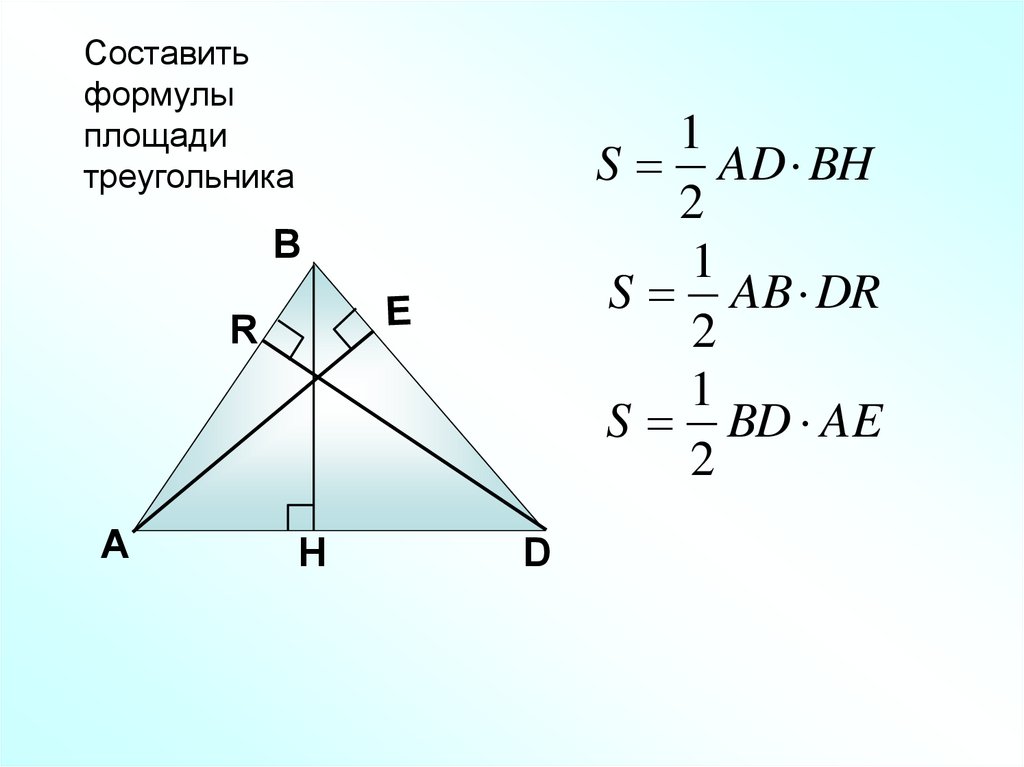
Составить
формулы
площади
треугольника
1
S AD BH
2
1
S AB DR
2
1
S BD AE
2
В
R
А
H
D

7.

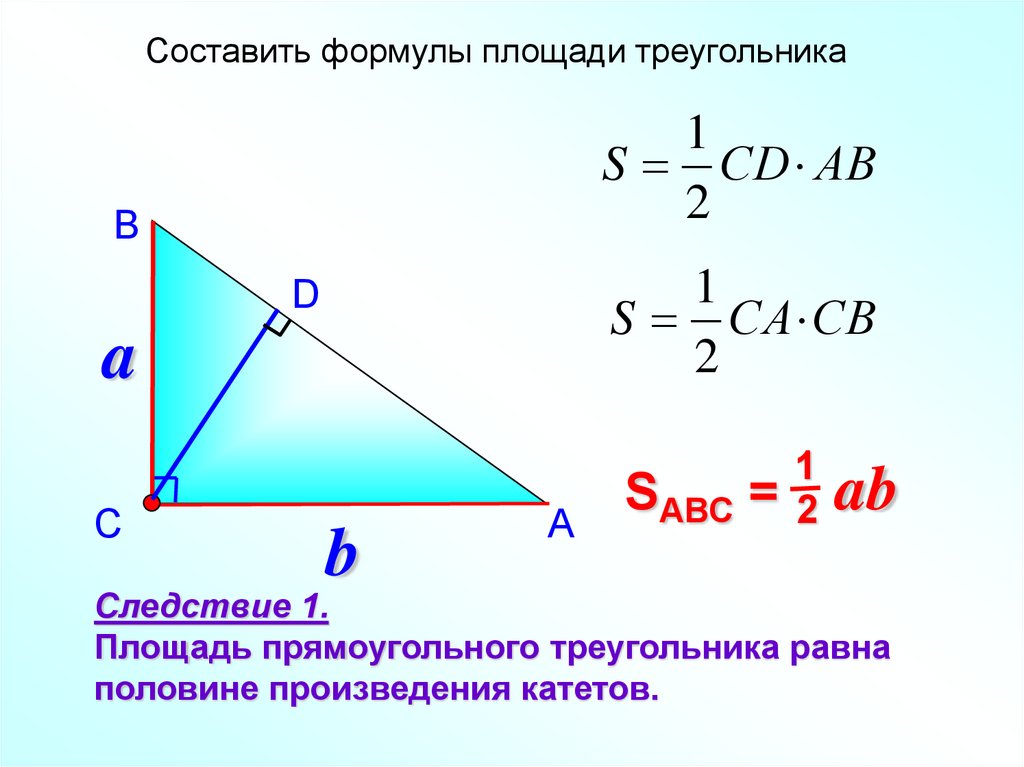
Составить формулы площади треугольника
1
S СD АB
2
В
1
S СА СB
2
D
a
С
b
А
SABC =
1
2
ab
Следствие 1.
Площадь прямоугольного треугольника равна
половине произведения катетов.

8.

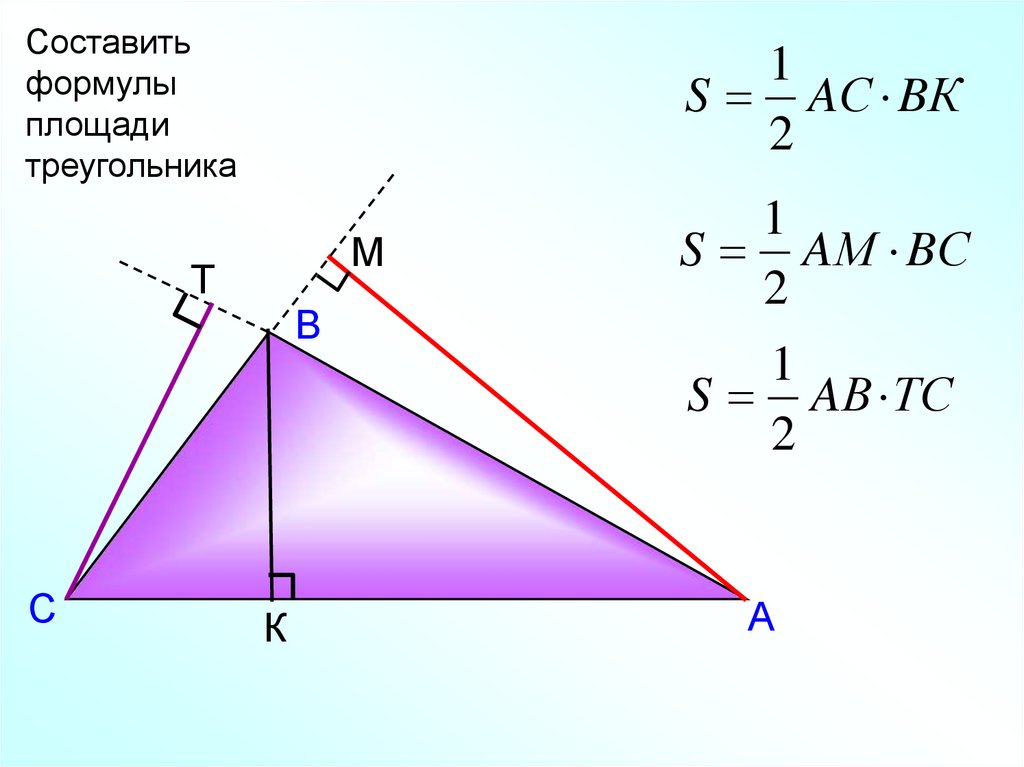
Составить
формулы
площади
треугольника
1
S AС BК
2
М
Т
В
С
К
1
S AМ BС
2
1
S AВ ТС
2
А

9.

АBC - треугольник
Найти площадь треугольника.
В
2
А
H
5
С

10.

АBC - треугольник
Найти площадь треугольника.
В
4
А
5
С

11.

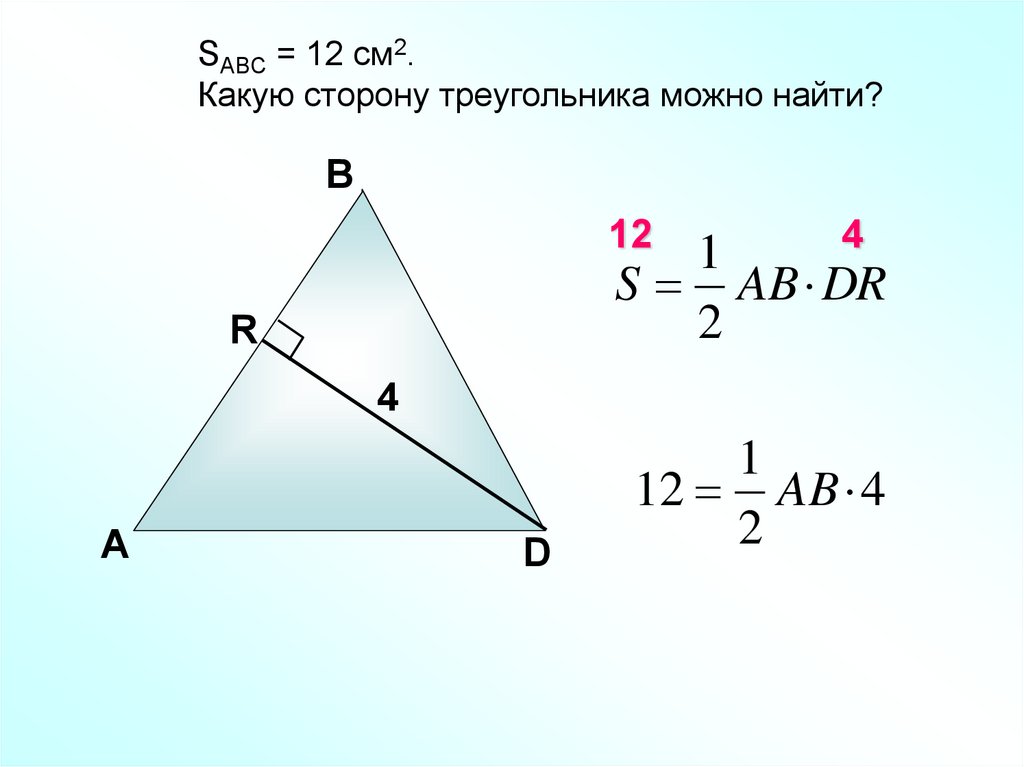
SABC = 12 см2.
Какую сторону треугольника можно найти?
В
12
4
1
S AB DR
2
R
4
А
D
1
12 AB 4
2

12.

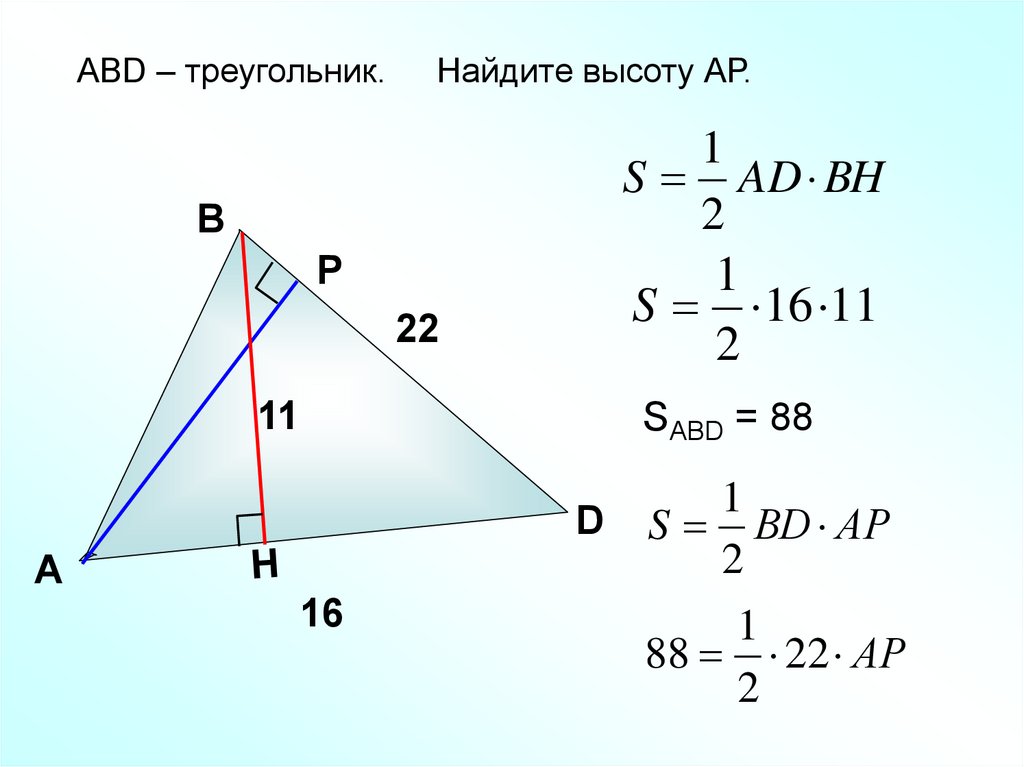
АBD – треугольник.
Найдите высоту АР.
1
S AD BH
2
В
Р
22
11
1
S 16 11
2
SABD = 88
1
D S ВD АР
2
А
16
1
88 22 АР
2

13.

Следствие 2. Если высоты двух треугольников равны,
то их площади относятся как основания.
В
С
М
H
1
S АВС ВH АC
2
=1
S MBN BH MN
2
N
А
SABC
SMBN
=
AC
MN

14.

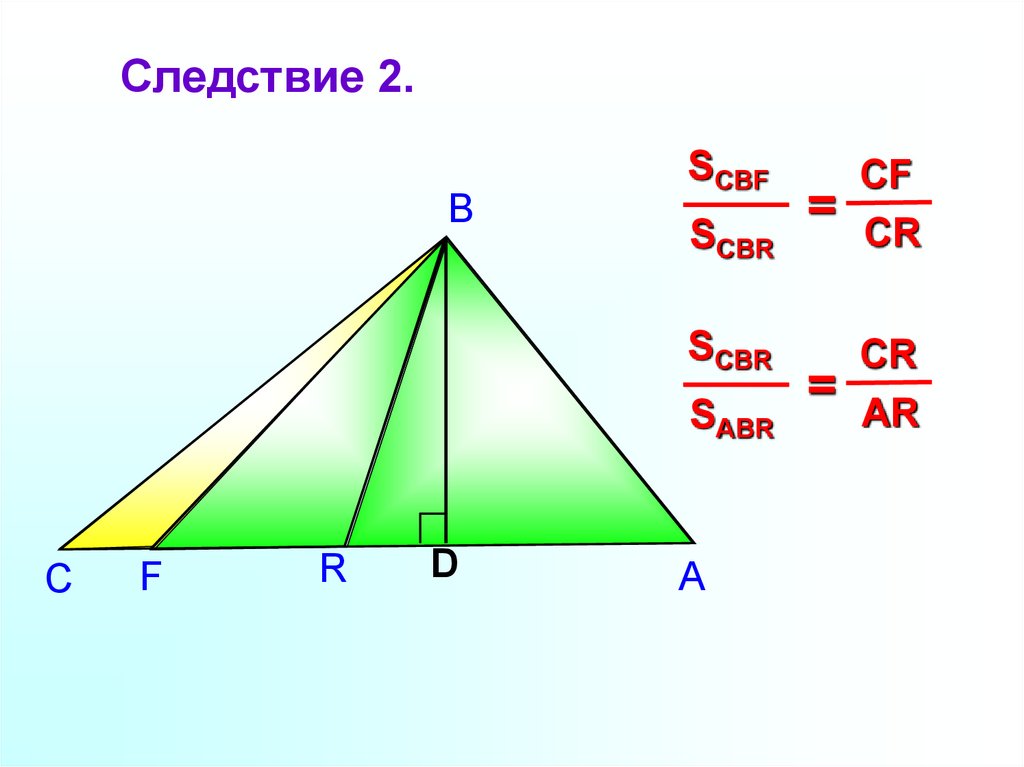
Следствие 2.
В
SCBF
SCBR
SCBR
SABR
С
F
R
D
А
=
CF
CR
=
CR
AR

15.

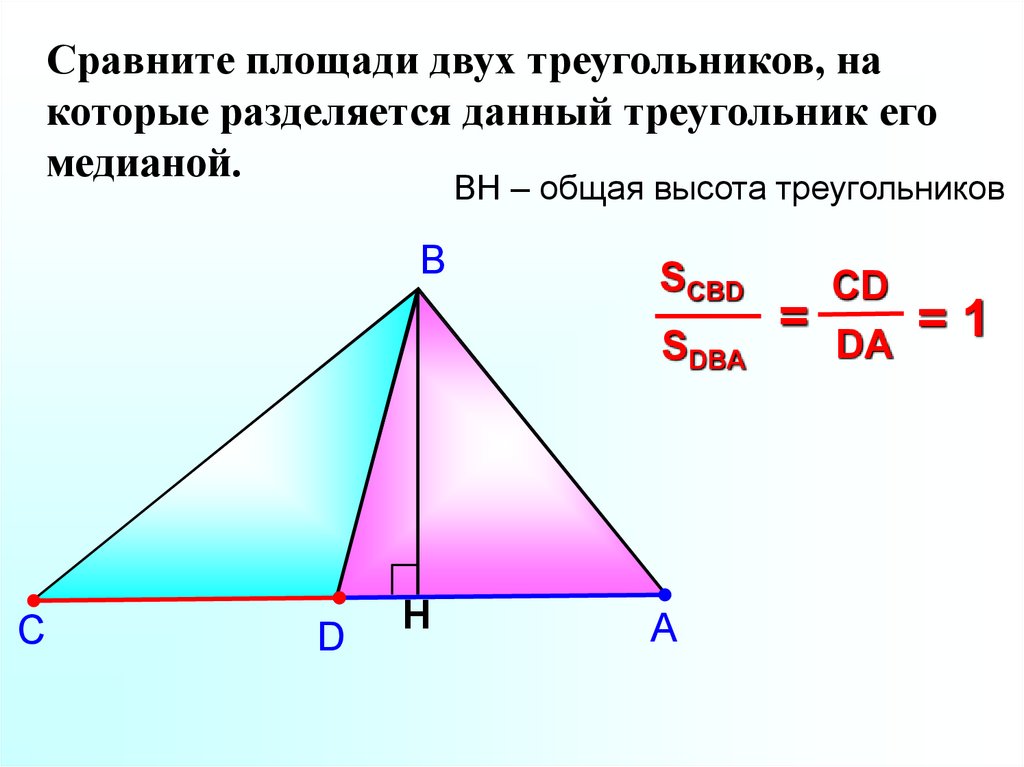
Сравните площади двух треугольников, на
которые разделяется данный треугольник его
медианой.
BH – общая высота треугольников
В
SCBD
SDBA
С
D
H
А
=
CD
DA
=1

16.

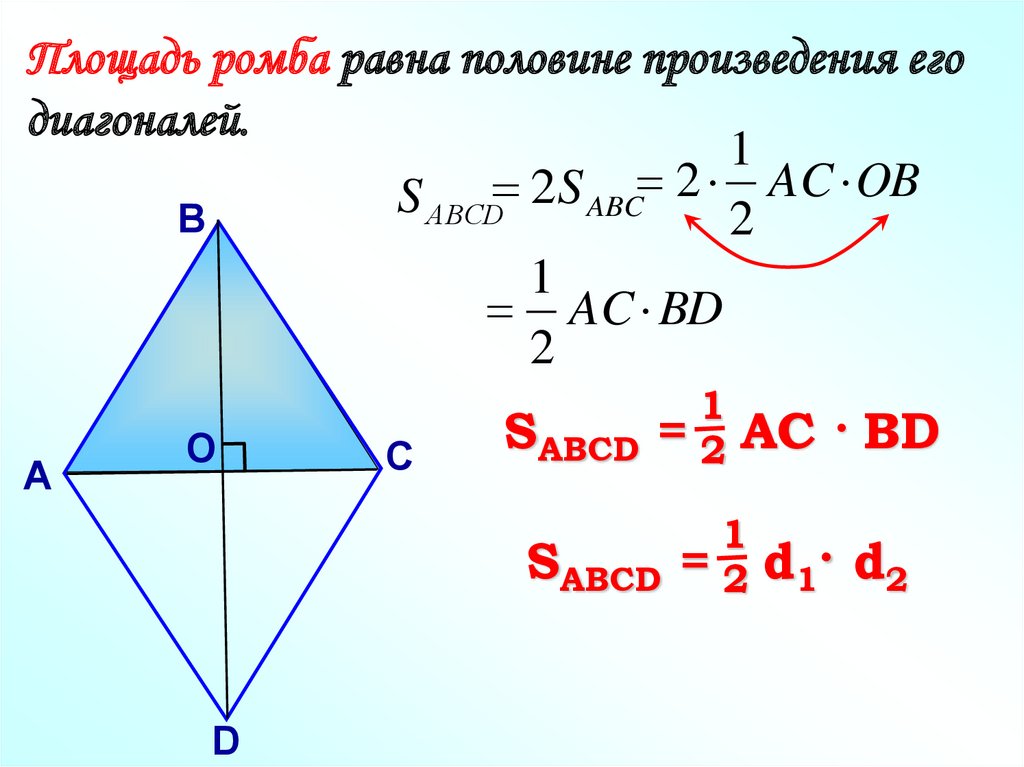
Площадь ромба равна половине произведения его
диагоналей.
1
2
AC
OB
2
S
S
ABC
АВСD
В
2
1
AC BD
2
А
О
С
1
SABCD = 2
AC · BD
1
SABCD = 2
D
d1· d2

17.

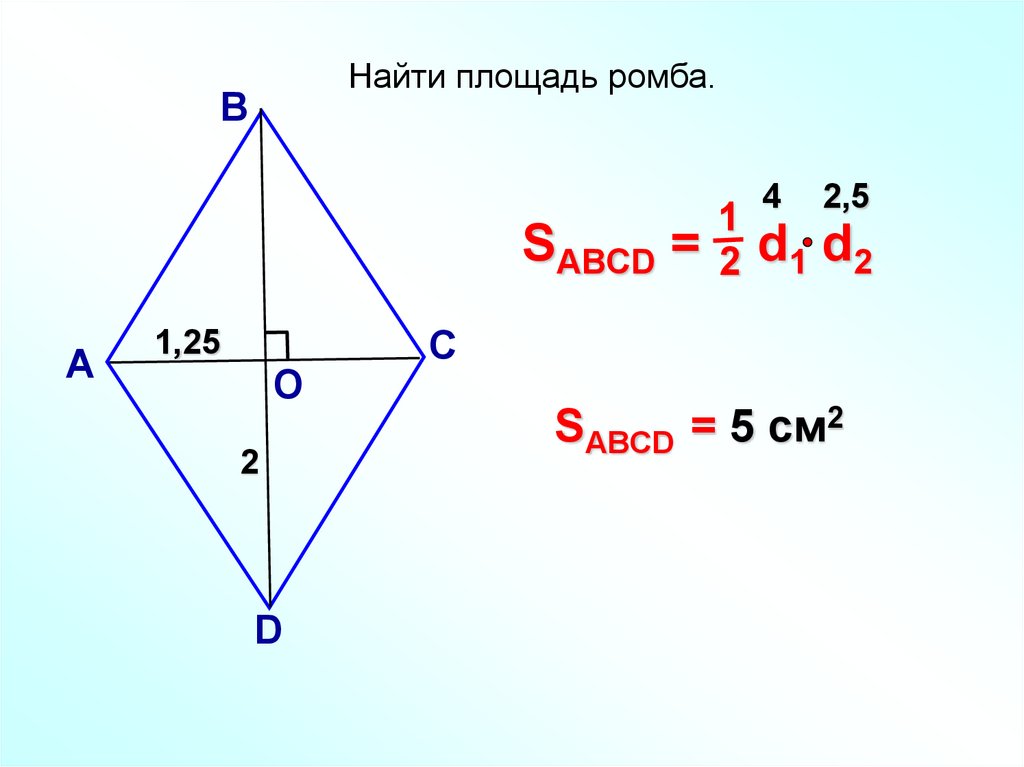
Найти площадь ромба.
В
SABCD =
А
1,25
О
2
D
1
2
4
2,5
d1 d2
С
SABCD = 5 см2

18.

Точка М лежит на основании АВ равнобедренного
∆ АВС. Найдите площадь этого треугольника, если
длины его боковых сторон АС и АВ равны 12 см, а
расстояния от точки М до этих сторон равны
соответственно 2 см и 5 см.
С
12
12
К
Р
2
А
5
М
В

19.

ТЕОРИЯ: стр. 123 – 124 выучить;
ЗАДАЧИ: № 464, 468, 470, 476

20.

21.

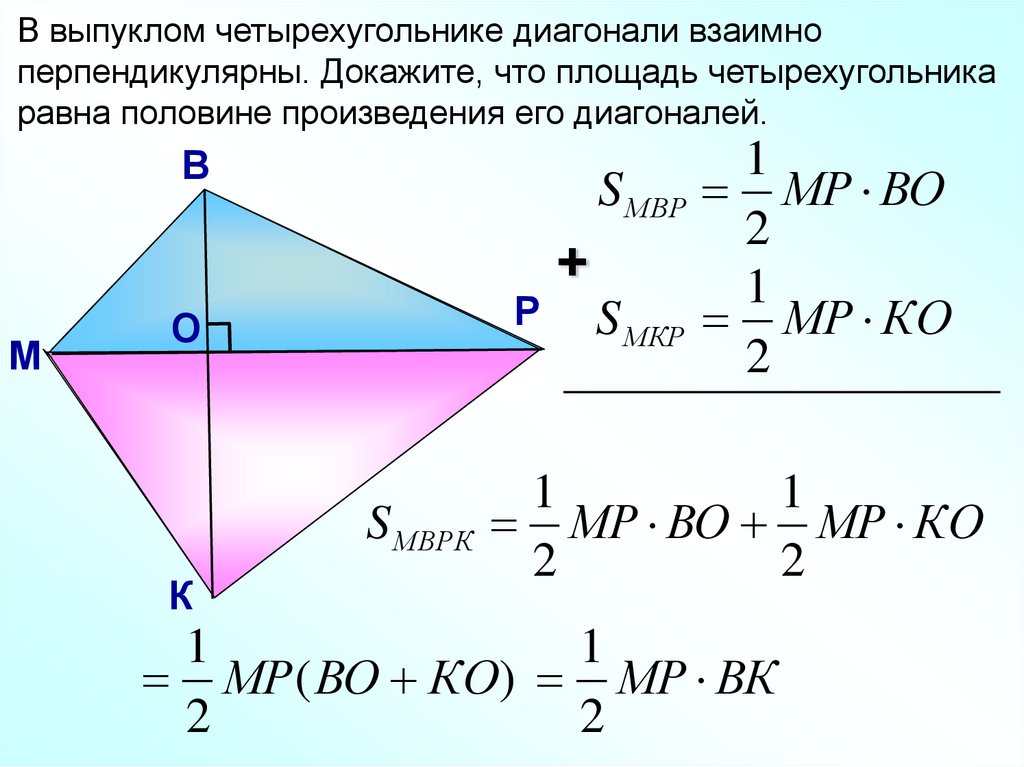
В выпуклом четырехугольнике диагонали взаимно
перпендикулярны. Докажите, что площадь четырехугольника
равна половине произведения его диагоналей.
В
М
S МВР
Р
О
S МВРК
К
+
S МКР
1
МР ВО
2
1
МР КО
2
1
1
МР ВО МР КО
2
2
1
1
МР ( ВО КО) МР ВК
2
2

22.

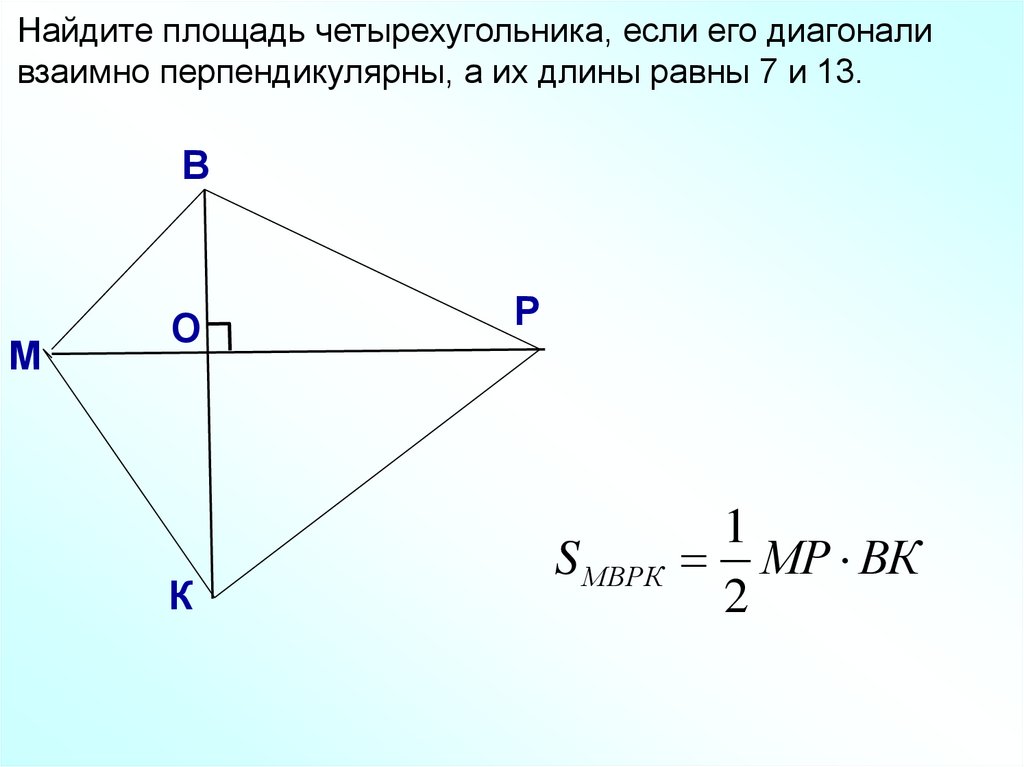
Найдите площадь четырехугольника, если его диагонали
взаимно перпендикулярны, а их длины равны 7 и 13.
В
М
О
К
Р
S МВРК
1
МР ВК
2

23.

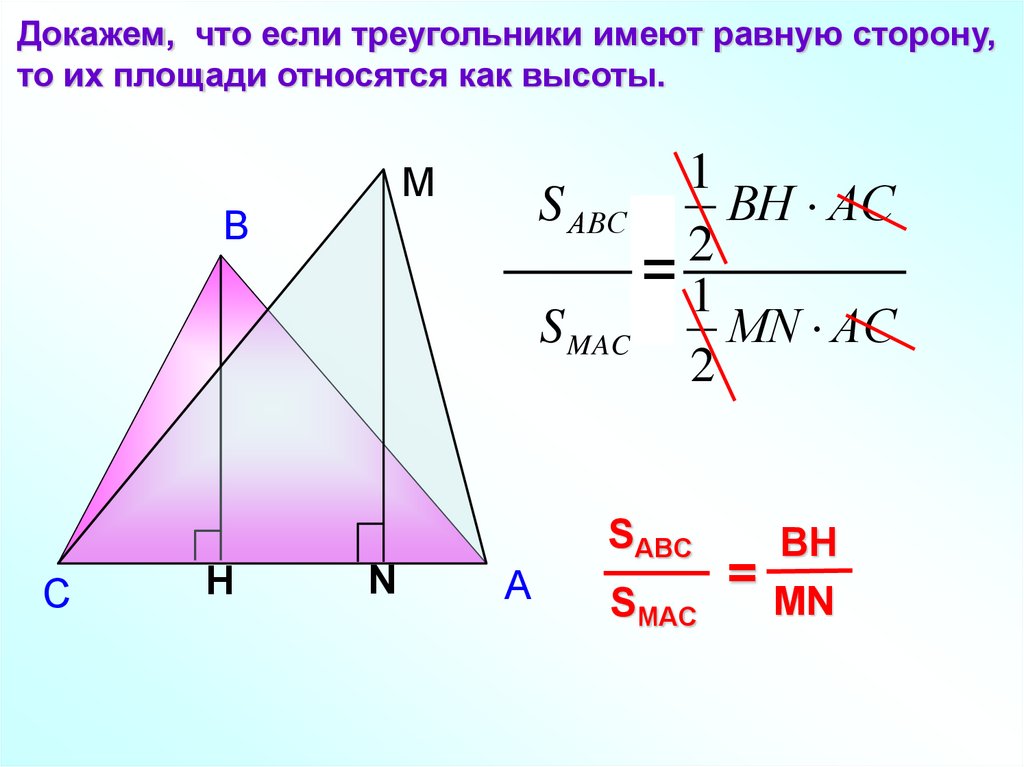
Докажем, что если треугольники имеют равную сторону,
то их площади относятся как высоты.
1
S АВС ВH АC
2
=1
S MAC МN АС
2
М
В
SABC
С
H
N
A
SMAC
=
BH
MN

24.

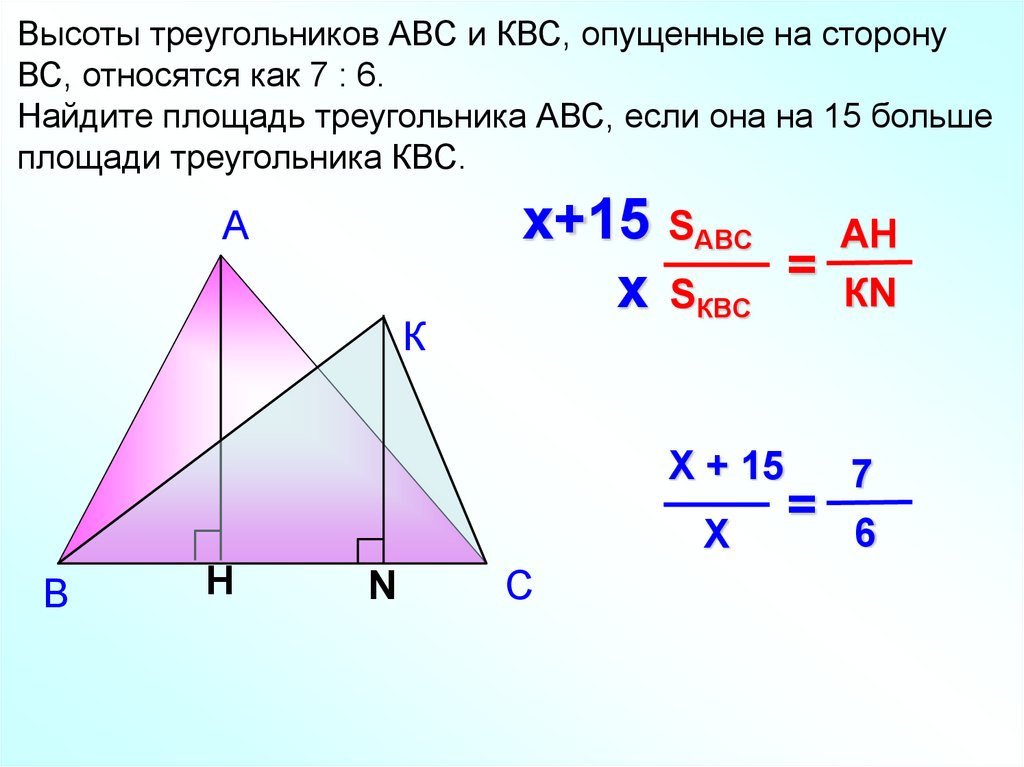
Высоты треугольников АВС и КВС, опущенные на сторону
ВС, относятся как 7 : 6.
Найдите площадь треугольника АВС, если она на 15 больше
площади треугольника КВС.
А
К
х+15
х
SABC
SКВC
Х + 15
Х
В
H
N
С
=
АH
КN
=
7
6