Similar presentations:
Пересечение поверхностей, метод вспомогательных концентрических сфер
1. Лекция 14 «Пересечение поверхностей, метод вспомогательных концентрических сфер»
12.
Для применения метода концентрических сфер необходимовыполнение трех условий:
1) Обе пересекающиеся поверхности должны быть поверхностями
вращения;
2) Оси поверхностей должны пересекаться;
3) Поверхности должны иметь общую плоскость симметрии, т.е.оси
поверхностей должны лежать в одной плоскости.
2
3.
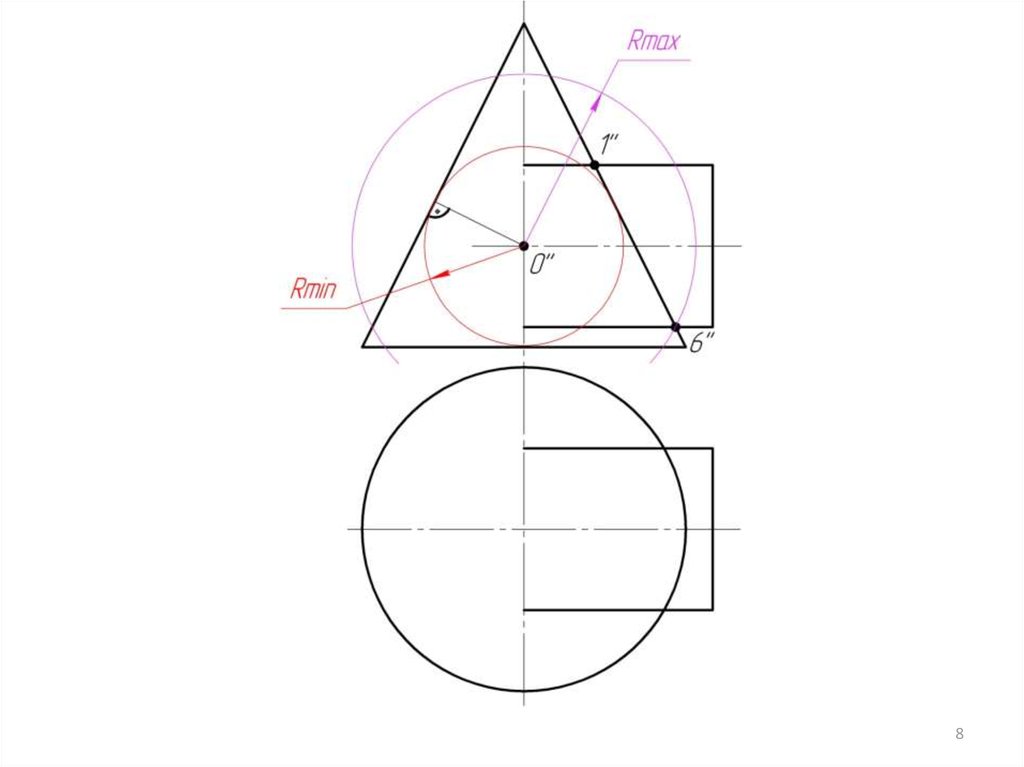
Алгоритм решения 2 ГПЗ.1. Находим центр секущих сфер – точку пересечения осей вращения
заданных поверхностей.
2. Находим минимальный радиус сферы (Rmin). Сфера минимального
радиуса должна одну поверхность пресекать, а другой касаться, т.е.
быть вписанной.
3. Находим радиус
максимальной секущей сферы, она должна
проходить через самую дальнюю точку пересечения очерков
поверхностей.
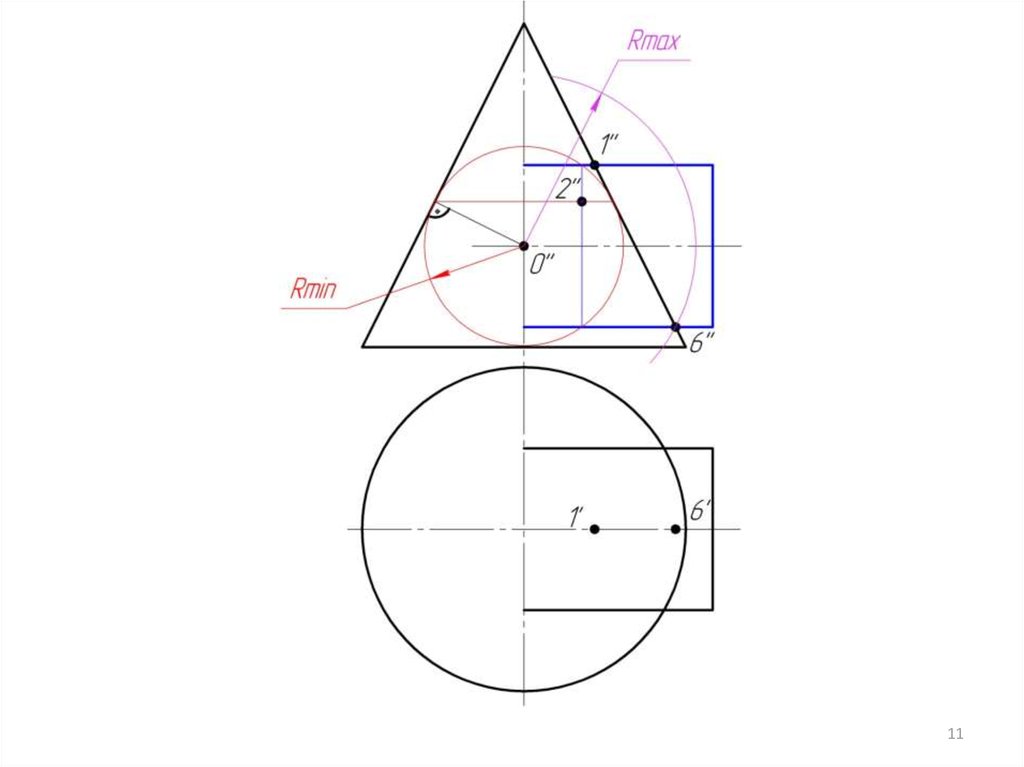
4. Строим линии пересечения сферы Rmin с заданными поверхностями.
5. Определяем точки пресечения построенных линий.
6. Произвольно выбираем последовательно ряд промежуточных секущих
сфер и повторяем построения по пунктам 4 и 5.
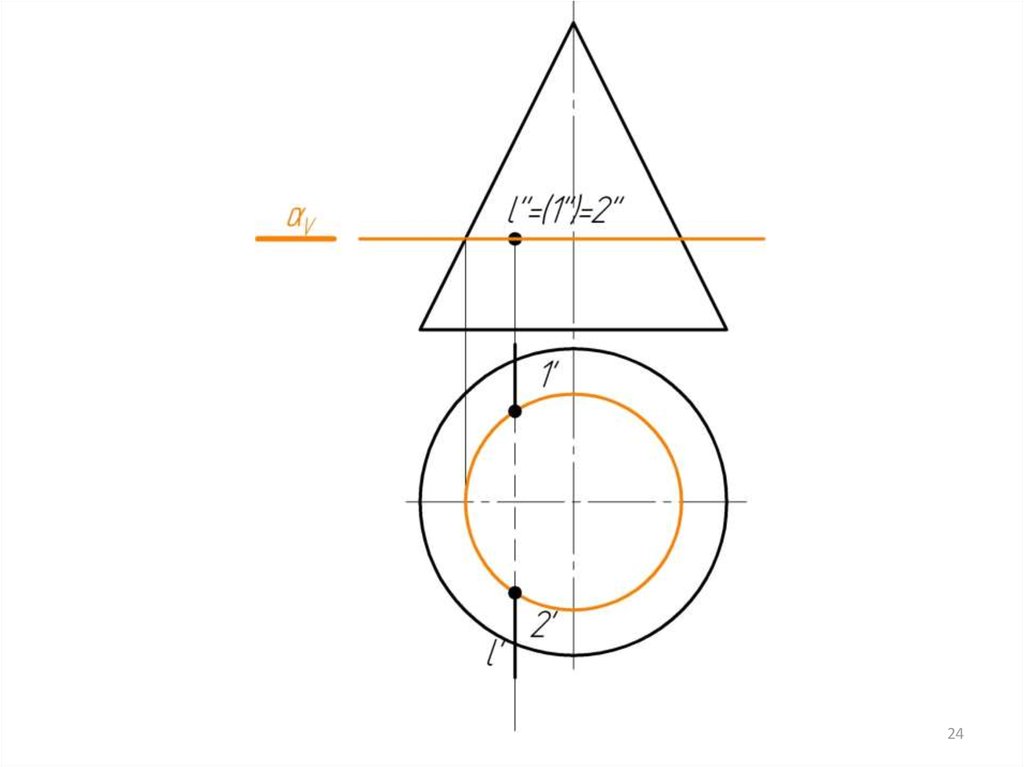
7. Соединяем точки плавной кривой линией с учетом видимости.
3
4.
45.
56.
67.
78.
89.
910.
1011.
1112.
1213.
1314.
1415.
1516.
1617.
1718.
1819.
1920. Лекция 15 «Пересечение прямой с поверхностью (1 ГПЗ)»
2021.
Алгоритм решения такой же как при пересечении прямой сплоскостью.
21
22.
2223.
2324.
2425.
2526.
2627.
2728.
2829.
2930.
Условие задачи: Определить точки пересеченияпрямой, заданной отрезком АВ, с поверхностью.
Решить вопрос видимости прямой.
30
31.
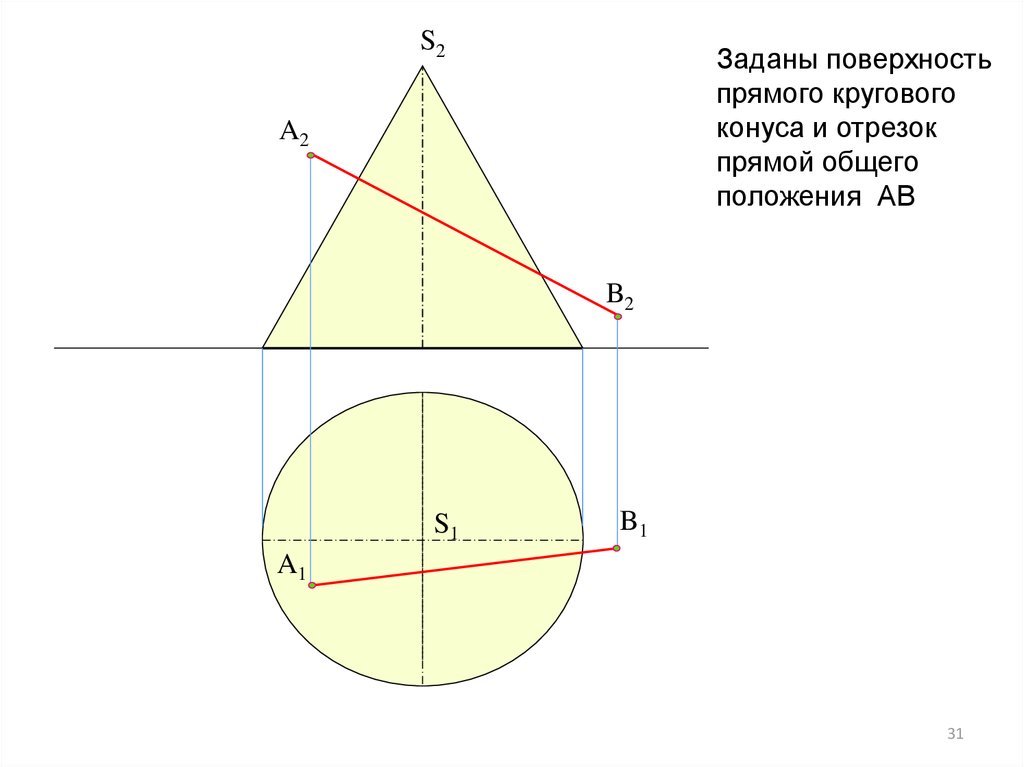
S2Заданы поверхность
прямого кругового
конуса и отрезок
прямой общего
положения АВ
A2
B2
S1
B1
A1
31
32.
S2A2
B2
S1
Для того, чтобы секущая
плоскость пересекла обе
фигуры по простым для
построения линиям, ее
надо задать «через»
прямую, так как
пересечением прямой и
плоскости, если прямая
принадлежит этой
плоскости, является сама
прямая.
B1
A1
32
33.
S2α2 A
2
B2
S1
A1
B1
Однако, если зададим
фронтально проецирующую
плоскость α (α2 ), то линией
пересечения этой плоскости с
поверхностью конуса будет
эллипс, что не является простой
для построения линией.
33
34.
S2A2
B2
S1
B1
Если зададим горизонтально
проецирующую плоскость α (α1),
то линией пересечения этой
плоскости с поверхностью конуса
будет гипербола, что так же не
является простой для построения
линией.
α1
A1
34
35.
S2A2
B2
S1
A1
Если в качестве посредника
воспользоваться плоскостью
общего положения и задать ее
через вершину конуса, то линией
B1 пересечения этой плоскости с
поверхностью будут две
пересекающиеся прямые.
35
36.
SРассмотрим решение задачи на
примере пространственной
модели. Следует иметь ввиду, что
линия среза (основание
конуса) должна принадлежать
плоскости проекций, или надо
дополнительно вводить плоскость
уровня П0 , чтобы основание
принадлежало этой плоскости. .
A
B
П0
36
37.
SЗададим плоскость общего
положения двумя
пересекающимися прямыми, одна
из которых - заданная АВ, а
другую зададим через вершину S
и точку на прямой АВ, например,
через точку А
( можно задать
любую другую точку на этой
прямой).
A
B
П0
37
38.
SПостроим следы плоскости
общего положения SАВ на
плоскости проекций (П0 ), для чего
найдем следы прямой S А (точка
М).
A
B
П0
M
38
39.
SПостроим следы плоскости
общего положения SАВ на
плоскости проекций (П0 ), для чего
найдем следы прямой S А (точка
М).
И следы прямой АВ (точка Т).
A
П0
B
Т
M
39
40.
SСледом плоскости общего
положения SАВ на плоскости
проекций (П0 ) является прямая
(отрезок) МТ. В этой же плоскости
П0 лежит основание конуса.
A
П0
B
Т
M
40
41.
Следом плоскости общегоположения SАВ на плоскости
проекций (П0 ) является прямая
(отрезок) МТ. В этой же плоскости
П0 лежит основание конуса.
S
Отмечаем точки 1 и 2 взаимного
пересечения основания конуса и
следа плоскости МТ.
A
П0
B
Т
M
2
1
41
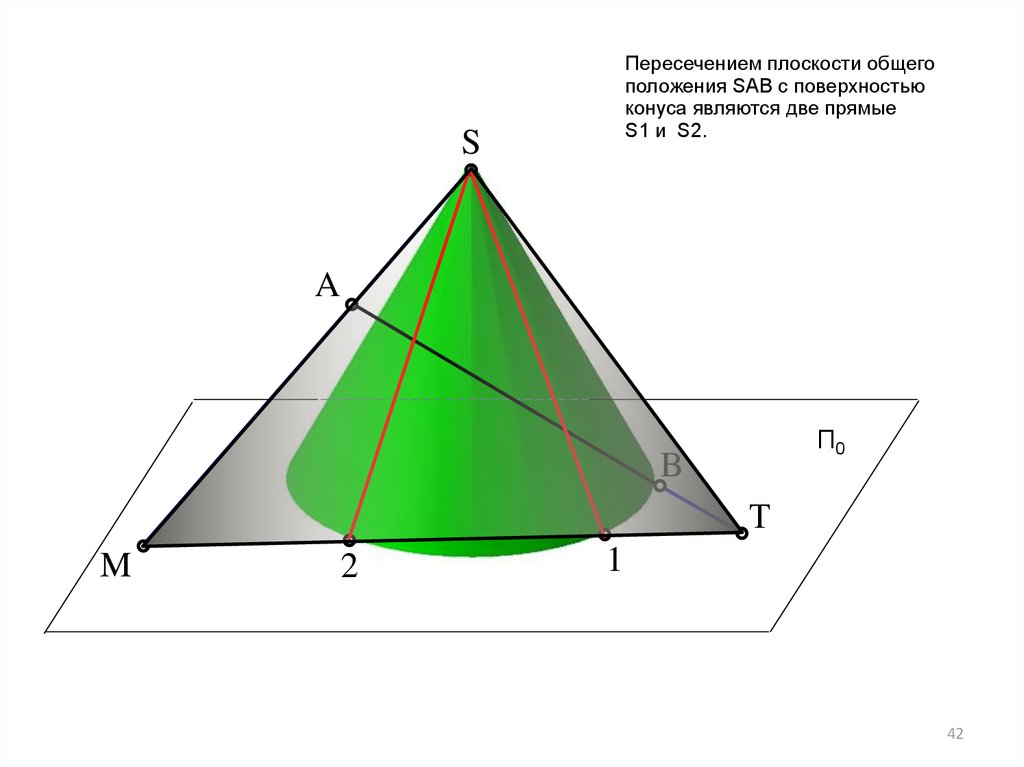
42.
Пересечением плоскости общегоположения SАВ с поверхностью
конуса являются две прямые
S1 и S2.
S
A
П0
B
Т
M
2
1
42
43.
Отрезки АВ, S1 и S2 принадлежатплоскости SМТ.
Следовательно, точки D и Е
(пересечение АВ с отрезками S1 и
S2) являются точками пересечения
АВ с поверхностью конуса.
S
A
C
D
П0
B
Т
M
2
1
43
44.
Отрезки АВ, S1 и S2 принадлежатплоскости SМТ.
Следовательно, точки D и Е
(пересечение АВ с отрезками S1 и
S2) являются точками пересечения
АВ с поверхностью конуса.
S
A
C
D
B
Т
M
2
1
44
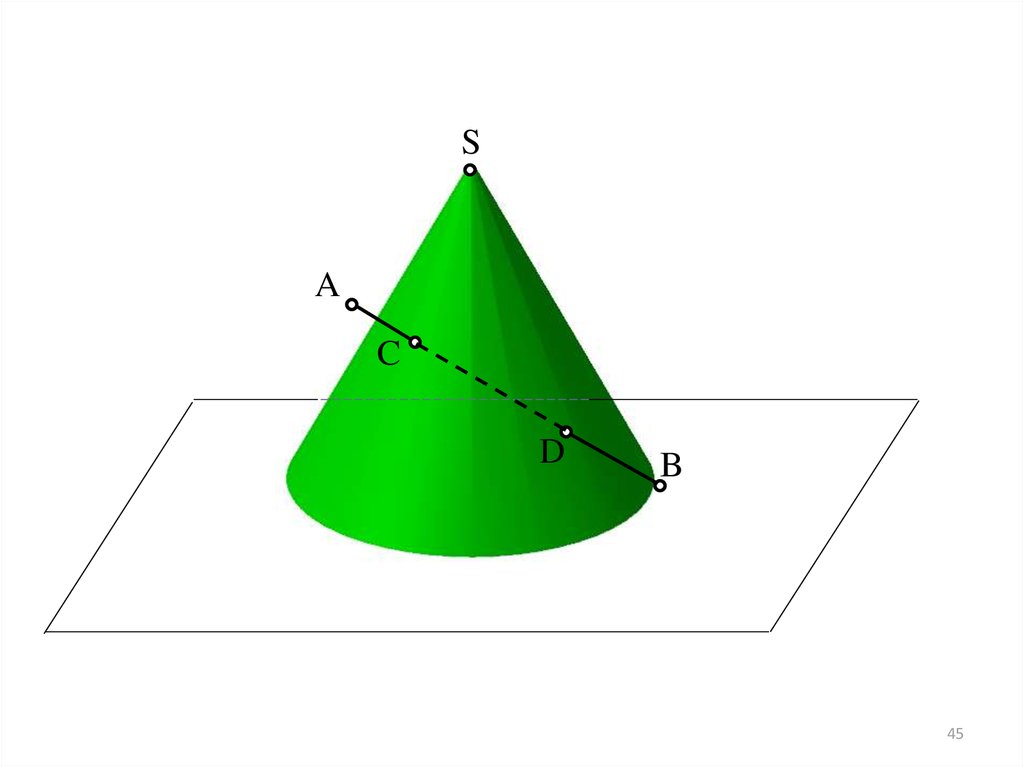
45.
SA
C
D
B
45
46.
SA
C
D
B
46
















































 mathematics
mathematics








