Similar presentations:
Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей
1. Взаимное пересечение поверхностей
Метод вспомогательных секущихплоскостей
2.
При пересечении поверхностей получаетсялиния, все точки которой принадлежат обеим
пересекающимся поверхностям – линия
пересечения.
Характер
линии
зависит
от
вида
поверхностей:
пересечение
многогранников
дает
ломаную линию;
пересечение многогранника и кривой
поверхности дает сочетание плоских
кривых линий (параболу, гиперболу, эллипс и
т.д.);
пересечение двух кривых поверхностей
дает пространственную кривую линию.
3.
Алгоритм решения задач1. Анализ поверхностей. Определить наличие
проецирующей поверхности. В этом случае на
одной из плоскостей проекций уже имеется
одна проекция линии пересечения.
2. Нахождение характерных точек.
3. Проведение вспомогательной секущей
плоскости, которая выбирается из условия
получения в сечении простых геометрических
фигур
–
окружностей,
треугольников,
прямоугольников.
4.
4. Построение двух линий пересеченияобеих поверхностей вспомогательной
секущей плоскостью.
5. Определение точек пересечения двух
построенных линий.
6. Повторение пунктов 3, 4, 5 – n раз.
7. Соединение полученных точек
пересечения линией.
8. Определение видимости линий
пересечения и линий заданных
поверхностей.
4
5.
56.
67.
78.
89.
910.
1011.
1112.
1213.
1314.
1415.
1516.
1617.
1718.
1819.
1920.
2021.
2122.
2223.
2324.
2425.
2526.
2627.
2728.
2829.
2930.
3031.
3132.
3233.
3334.
3435.
3536.
3637.
3738.
3839.
3940.
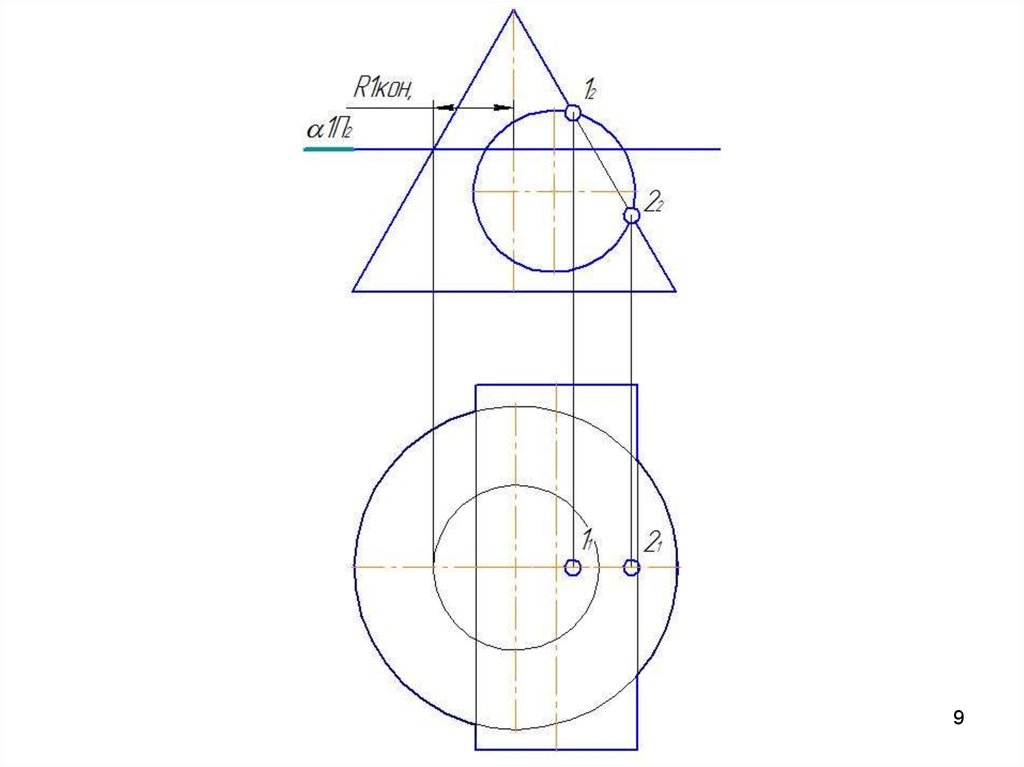
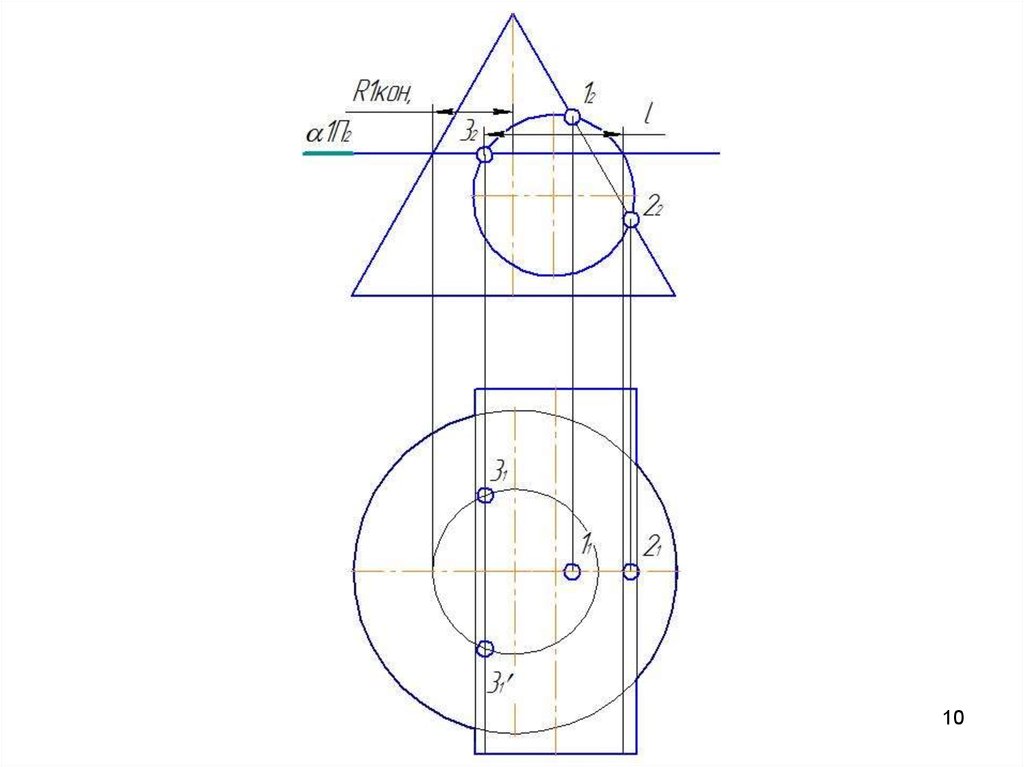
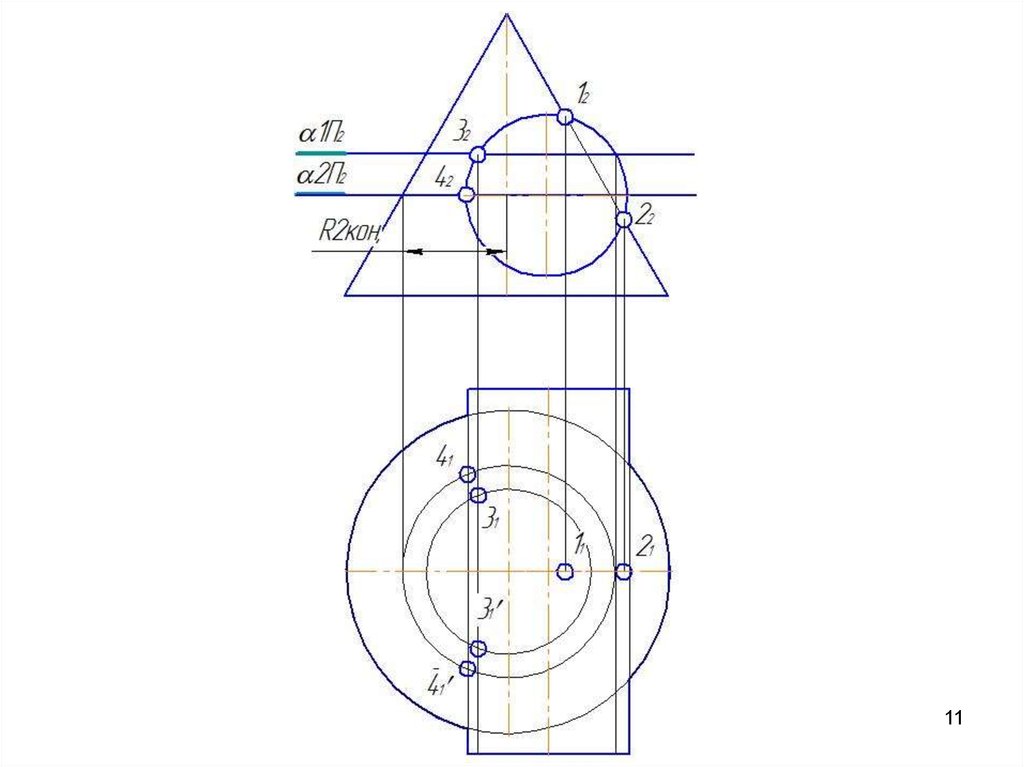
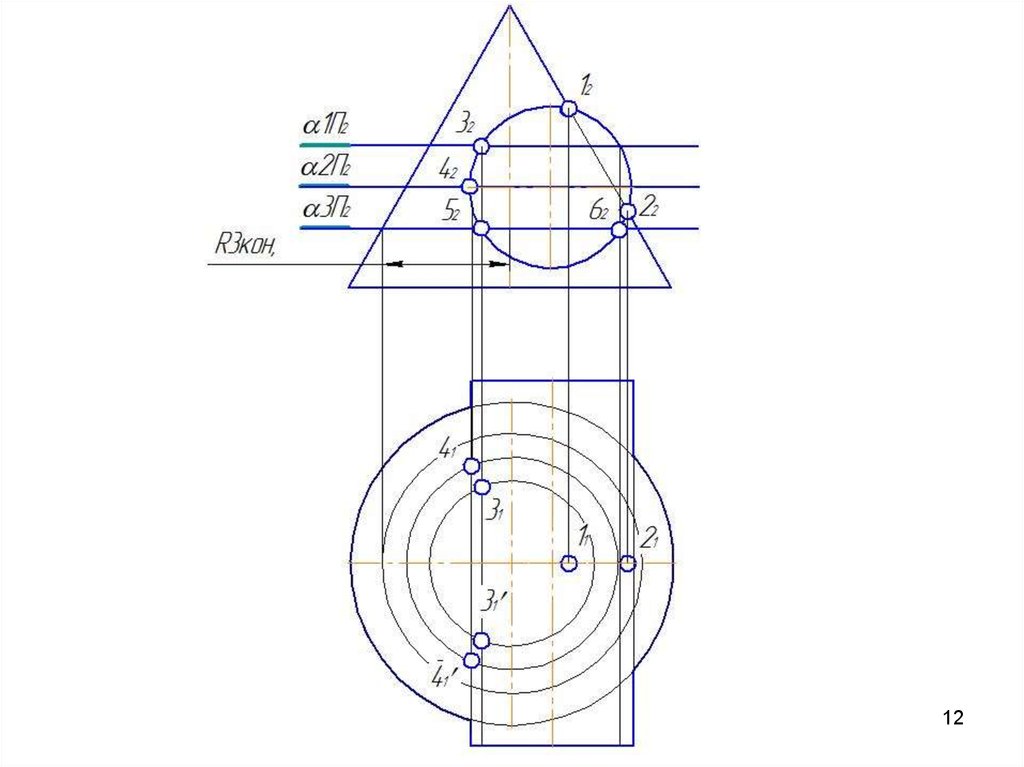
4041. Метод вспомогательных секущих плоскостей
Дано: цилиндр иконус.
11
1122
4
422
511
5
(52)
62 (72)
2
222 32
311
71
1111
411
4
611
211
2
Конус:
Øк=80 мм;
Нк=80 мм.
Цилиндр: Øц=80 мм;
Нц=90 мм.
Расстояние между
осями 20 мм.
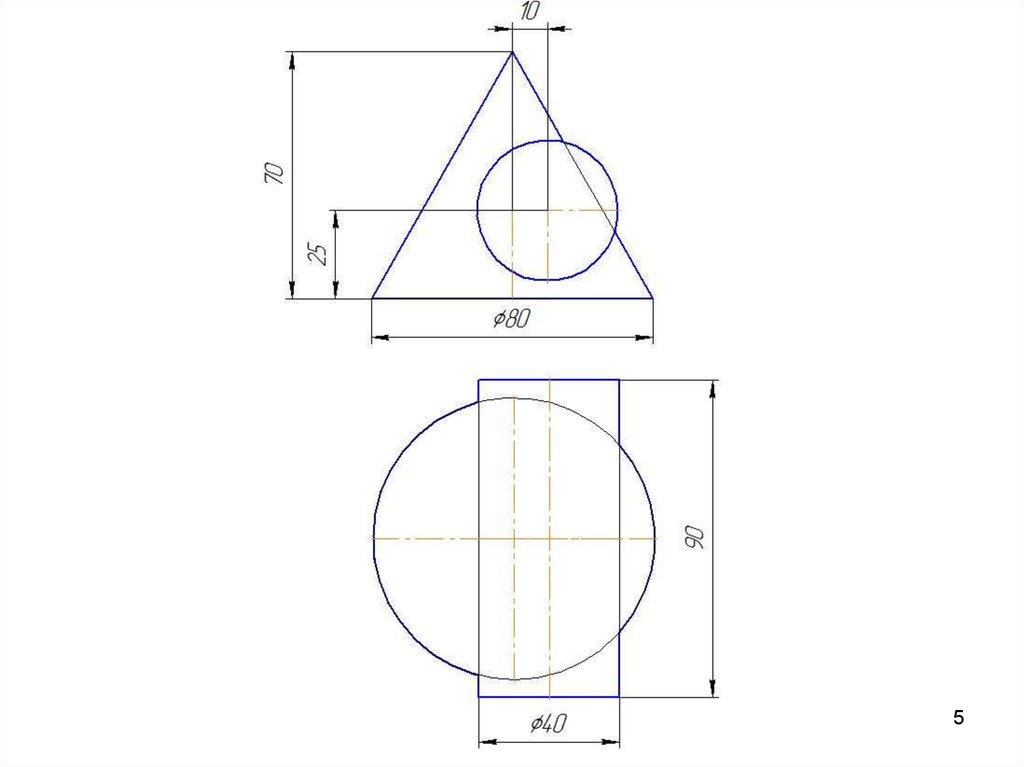
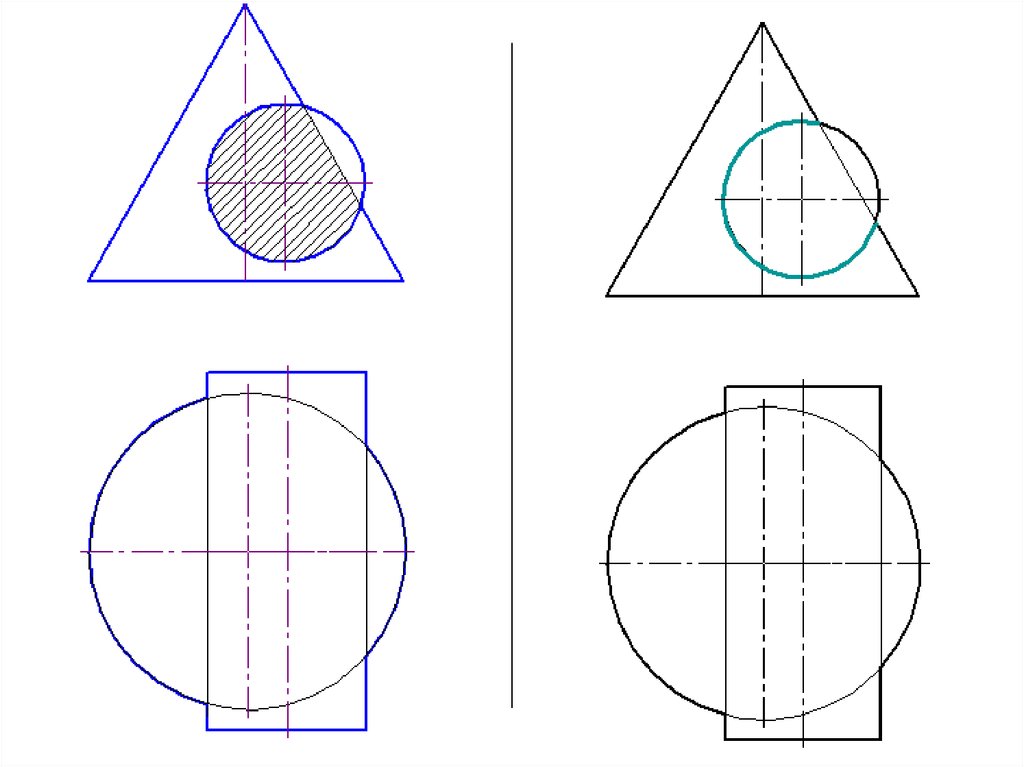
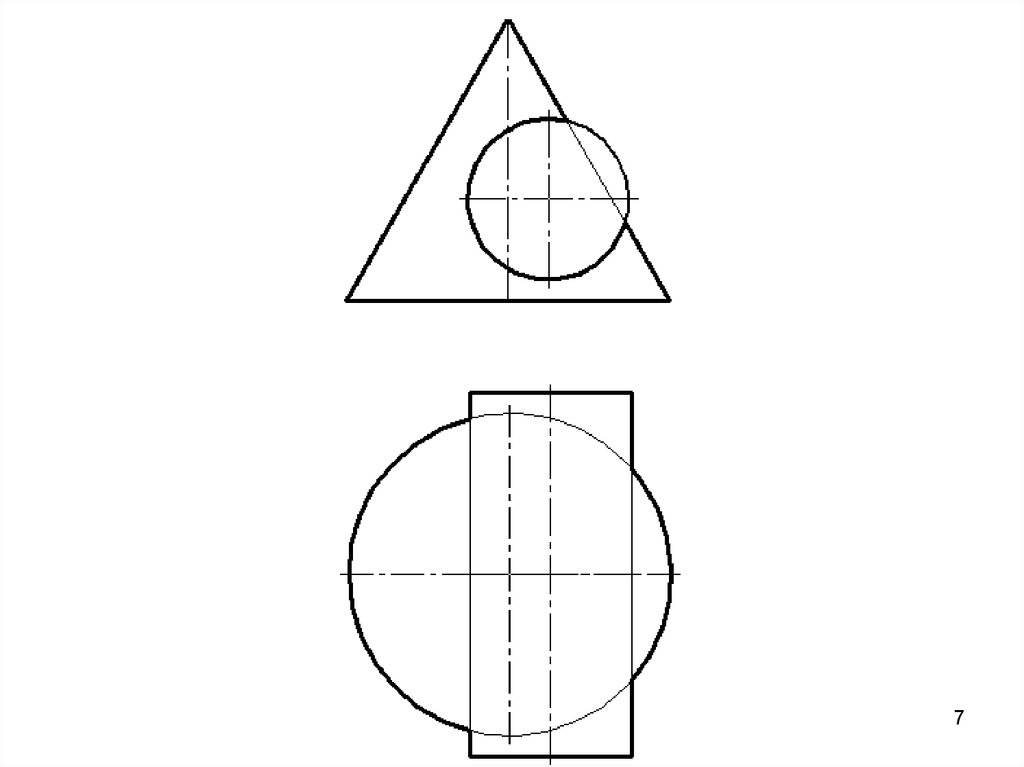
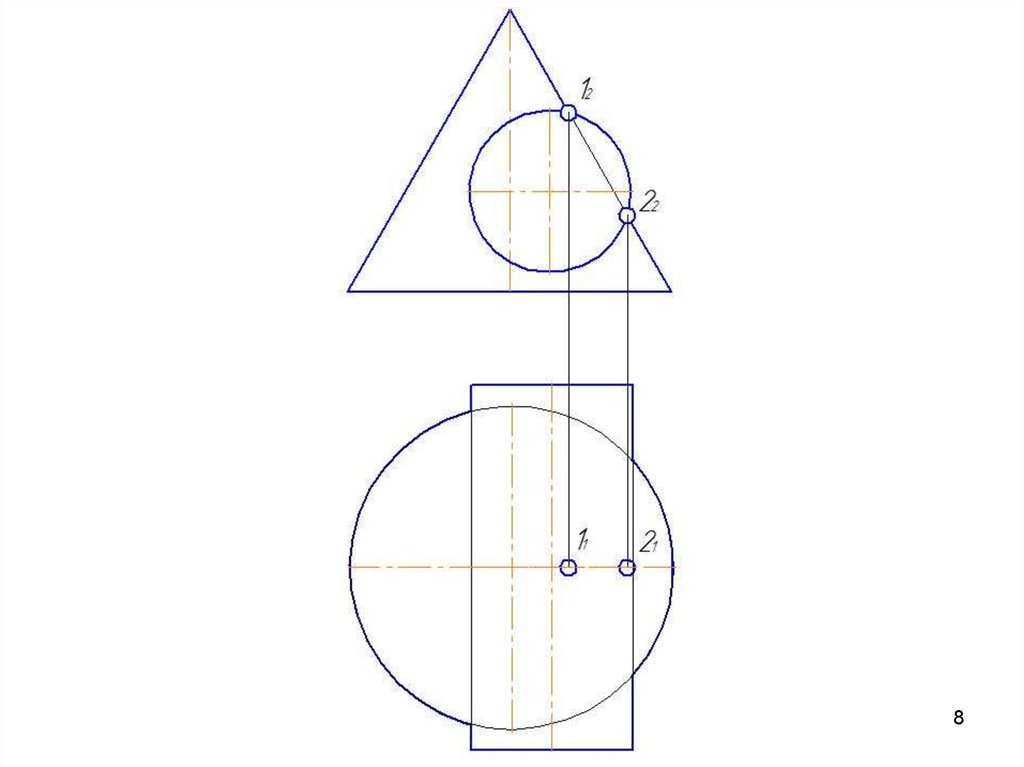
42. Метод вспомогательных секущих плоскостей
Дано: конус и сфера.11
22
2
2
2
2
Сфера: R=45 мм.
1 22 522 (622)
Расстояние между
722 (822) 422 322 осями 20 мм.
311
61161 811
1 11
511 71
1
51
Конус: Øк=80 мм;
Нк=70 мм.
Построить линию
пересечения поверхностей.
Определить участки
видимости линий.
43.
Взаимное пересечениеповерхностей
Метод секущих сфер
43
44. Частные случаи пересечения поверхностей вращения
Соосные поверхности - поверхностивращения, имеющие общую ось вращения.
Все линии пересечения - окружности.
На плоскость проекций, параллельную
осям вращения, они проецируются в виде
отрезка прямой линии, соединяющего
точки пересечения очерковых образующих.
44
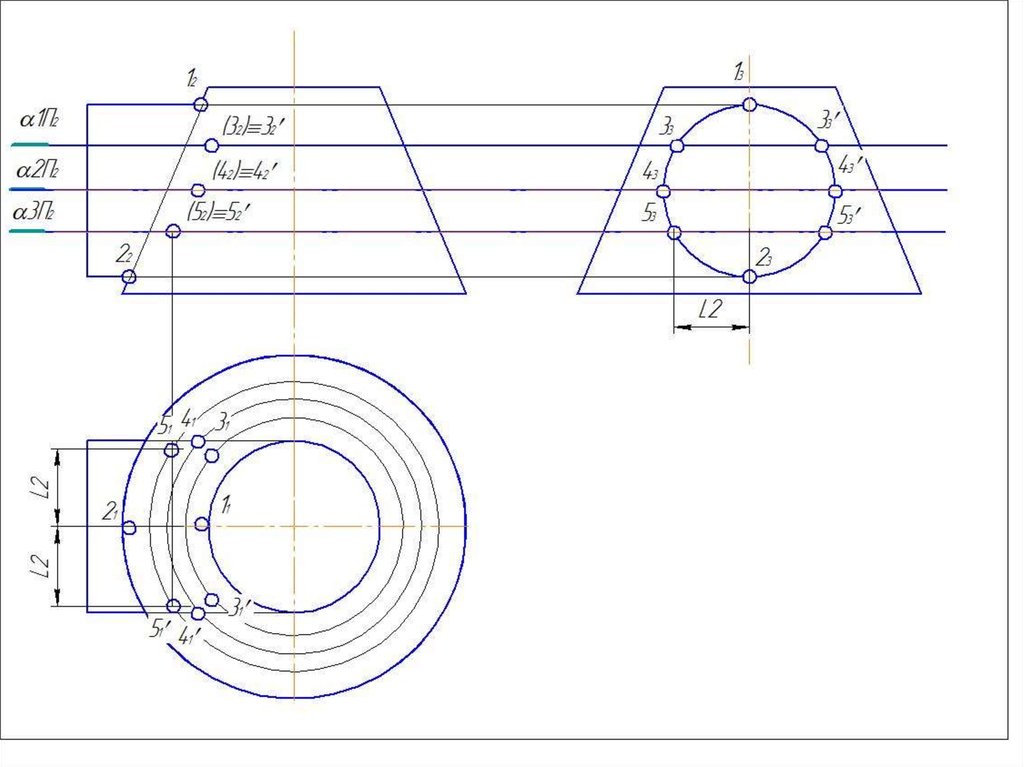
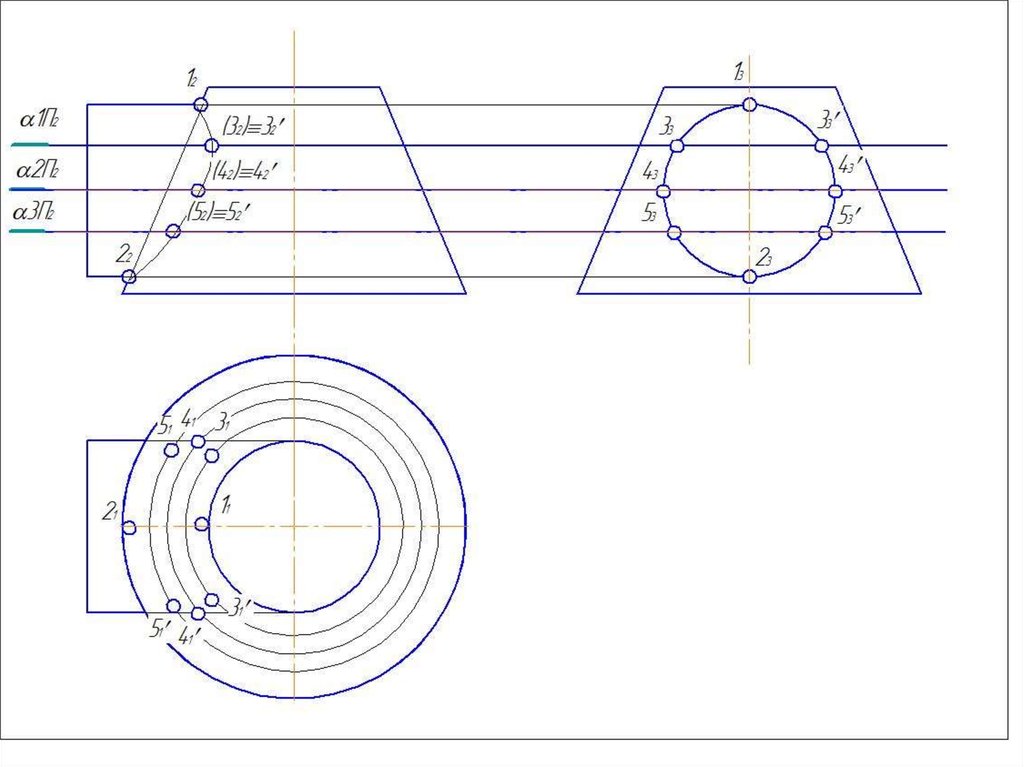
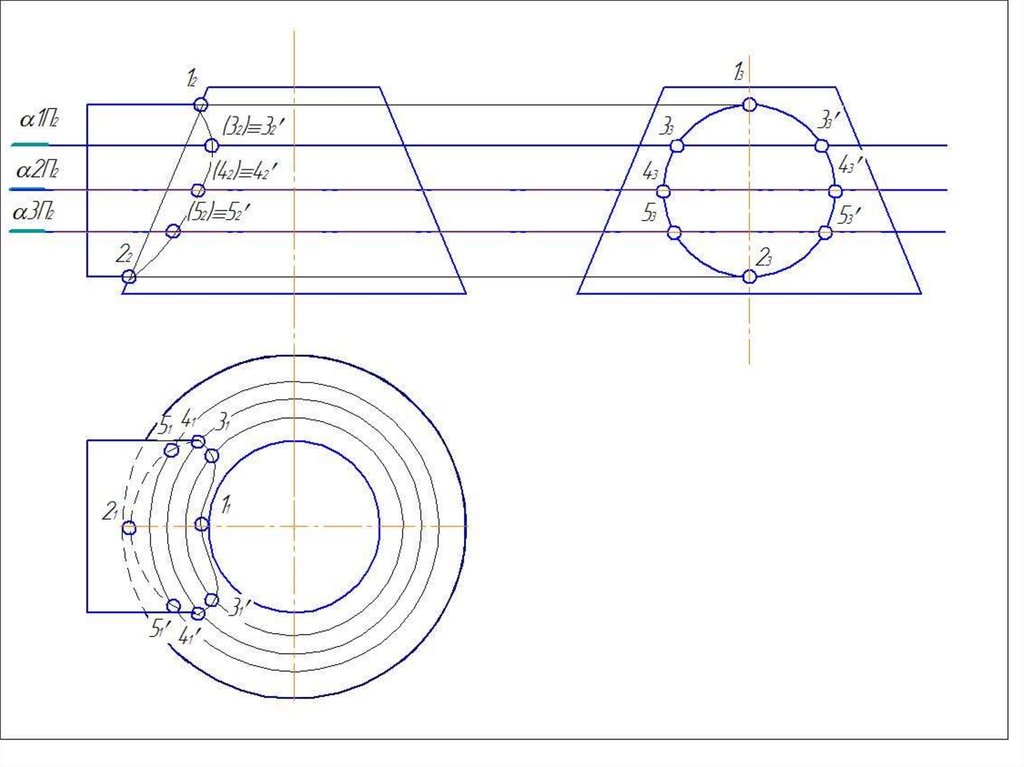
45. Частные случаи пересечения поверхностей вращения
Линии пересечения – окружности проецируются45в прямые, называемые параллели
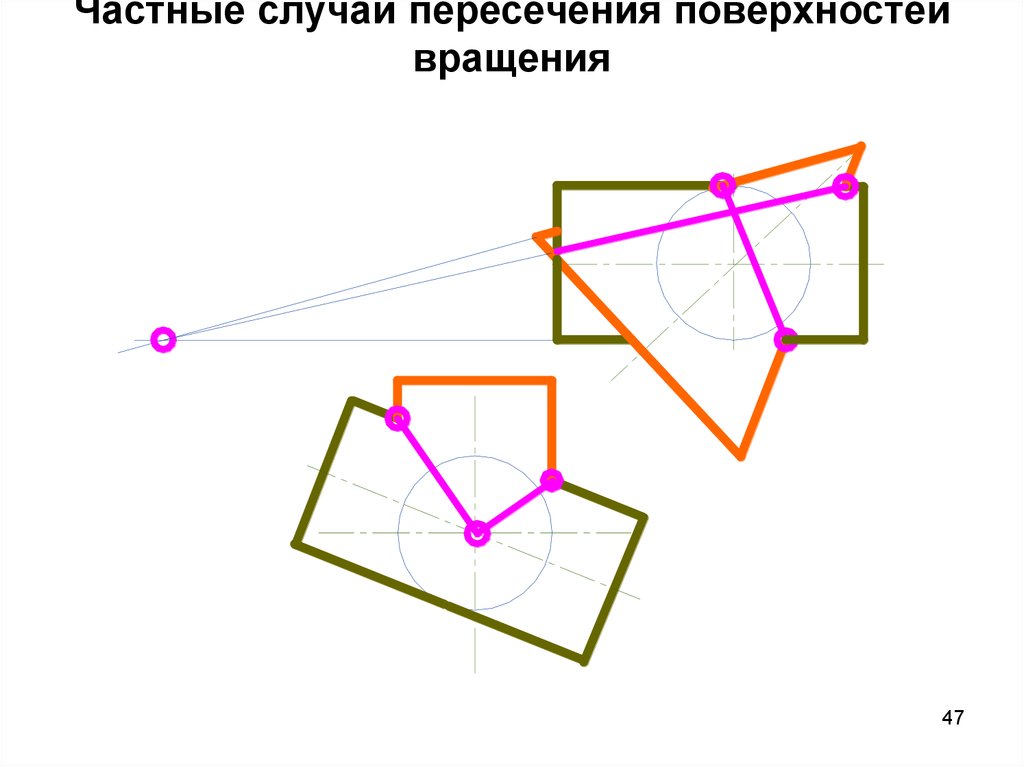
46. Частные случаи пересечения поверхностей вращения
Теорема Монжа: две поверхностивращения, описанные вокруг третьей,
пересекаются между собой по двум
кривым
второго
порядка,
которые
проецируются
на
плоскость,
параллельную осям вращения в виде
прямолинейных отрезков, соединяющих
точки
пересечения
очерковых
образующих.
46
47. Частные случаи пересечения поверхностей вращения
4748.
Применение методаконцентрических сфер возможно при
выполнении следующих условий:
1.Обе поверхности вращения.
2.Оси поверхностей пересекаются.
3.Поверхности
симметрии.
имеют
плоскость
48
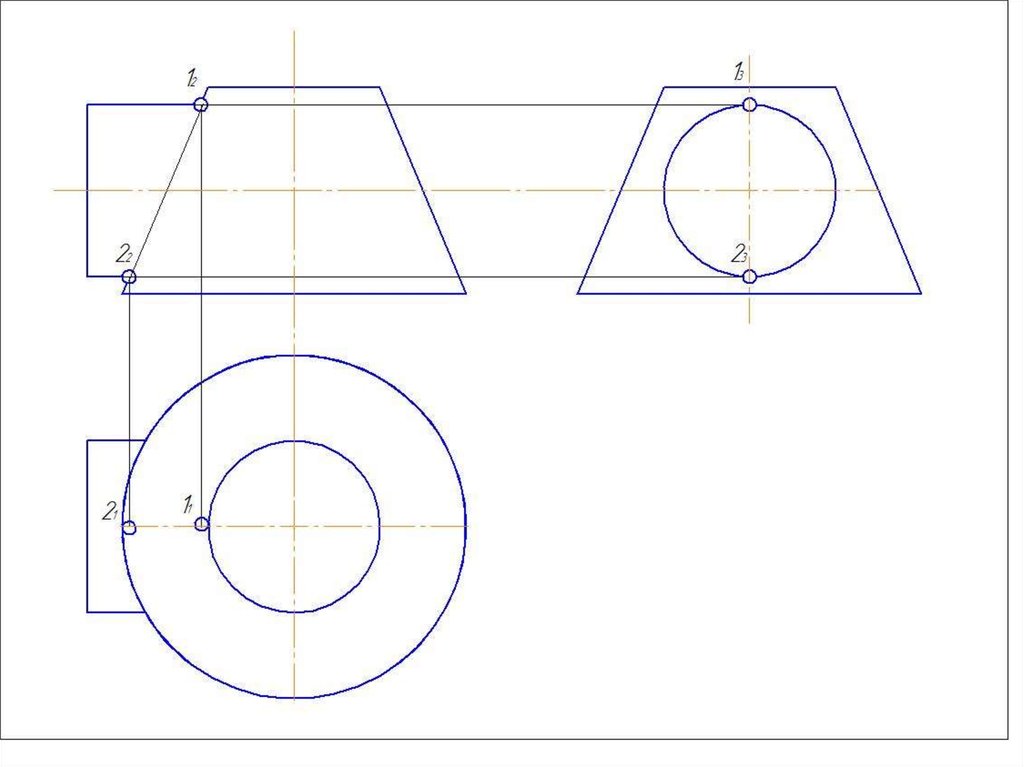
49. Алгоритм решения задач по построению линии пересечения поверхностей методом вспомогательных концентрических сфер
1.Провести анализ поверхностей:• обе поверхности вращения;
• оси поверхностей пересекаются
• поверхности имеют плоскость симметрии.
2. Определить центр вспомогательных
концентрических сфер - это точка пересечения
осей вращения.
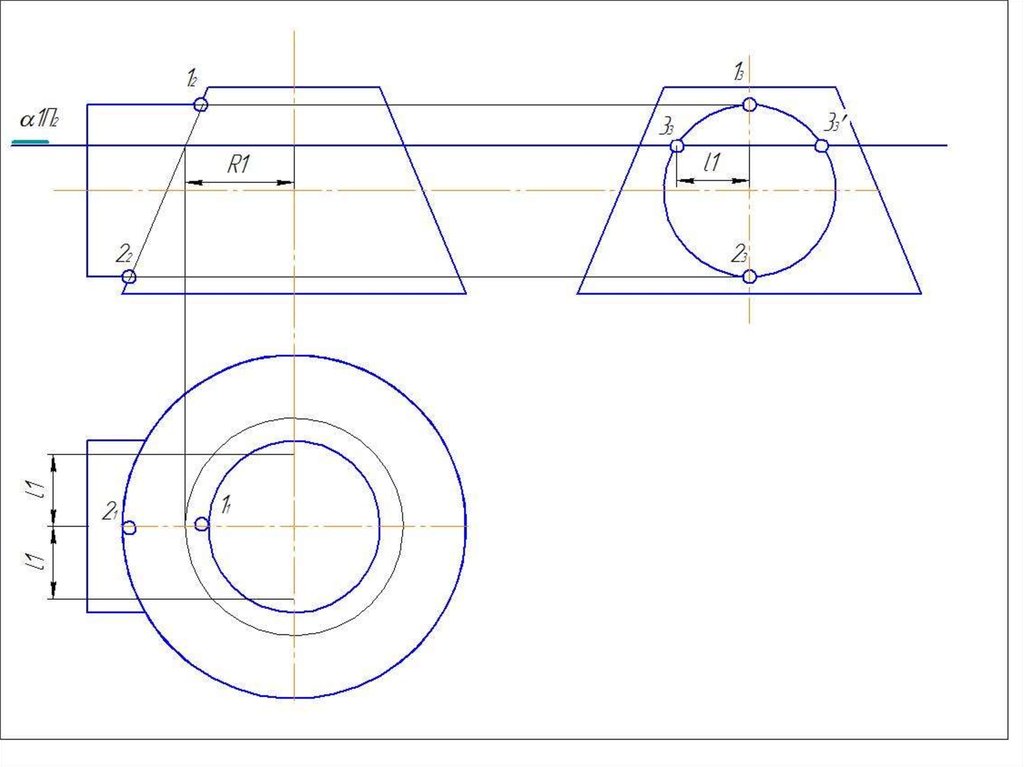
3. Определить радиус минимальной вписанной
сферы – Rmin. (Сфера данного радиуса должна
касаться большего из тел и пересекать меньшее из
49
тел).
50.
4. Построить параллель для сферы(Rmin.) касающейся с большей поверхностью и
параллель (или параллели) для сферы (Rmin.)
пересекающей меньшую поверхность.
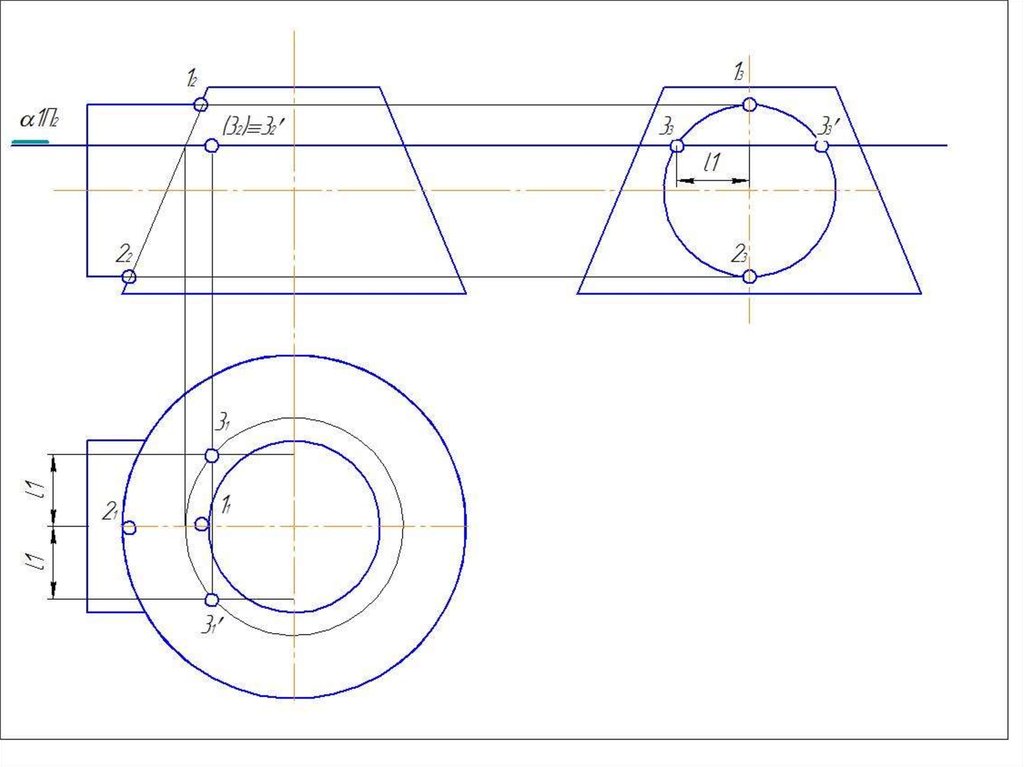
5. Найти точки пересечения построенных
параллелей, которые принадлежат линии
пересечения заданных поверхностей.
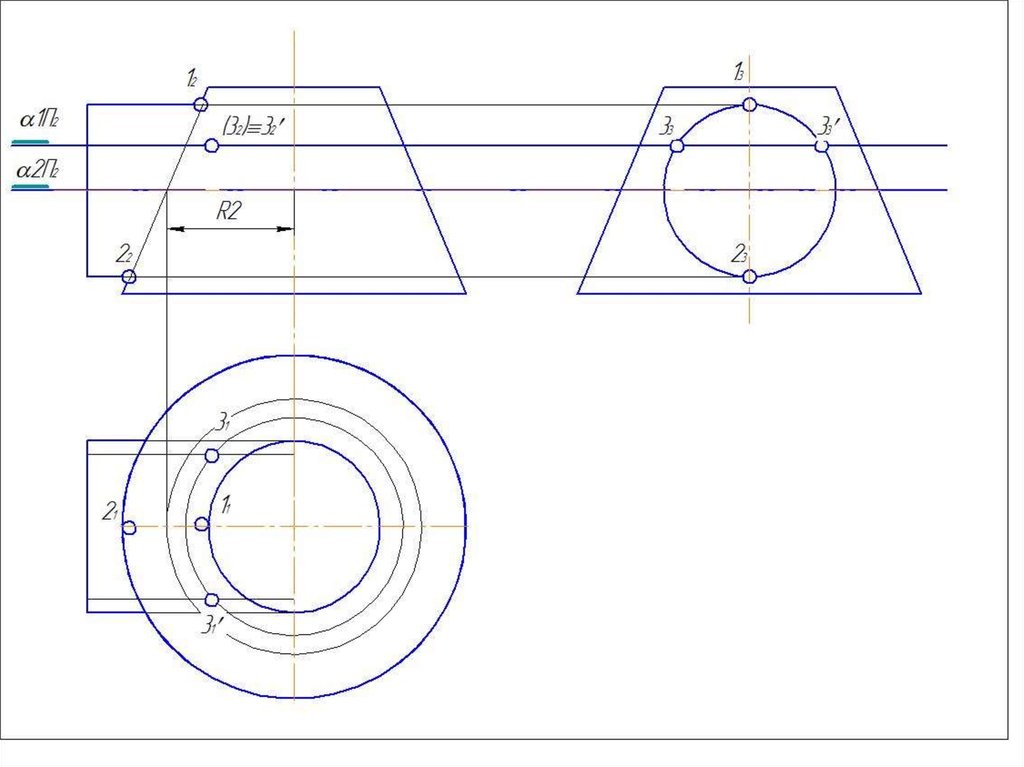
6. Построить несколько сфер большего
радиуса Rmin< R>Rmax.
7.Определить параллели и точки их
пересечения.
8. Соединить точки плавной линией.
9.Определить
видимость
линий
выполненного изображения.
50
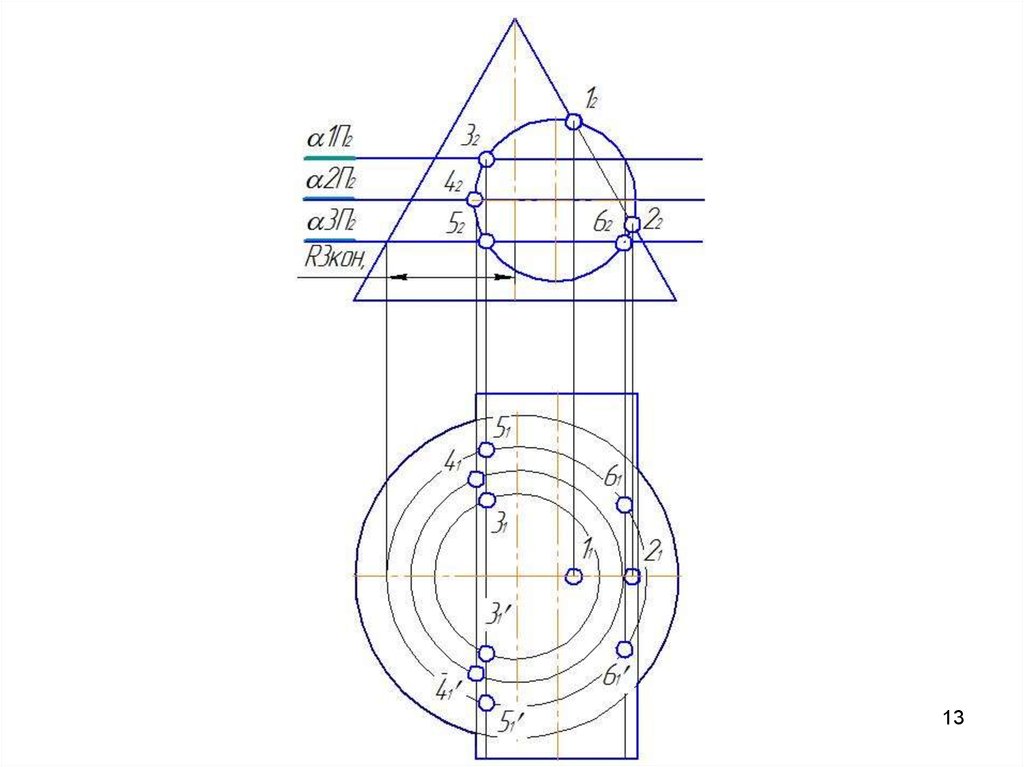
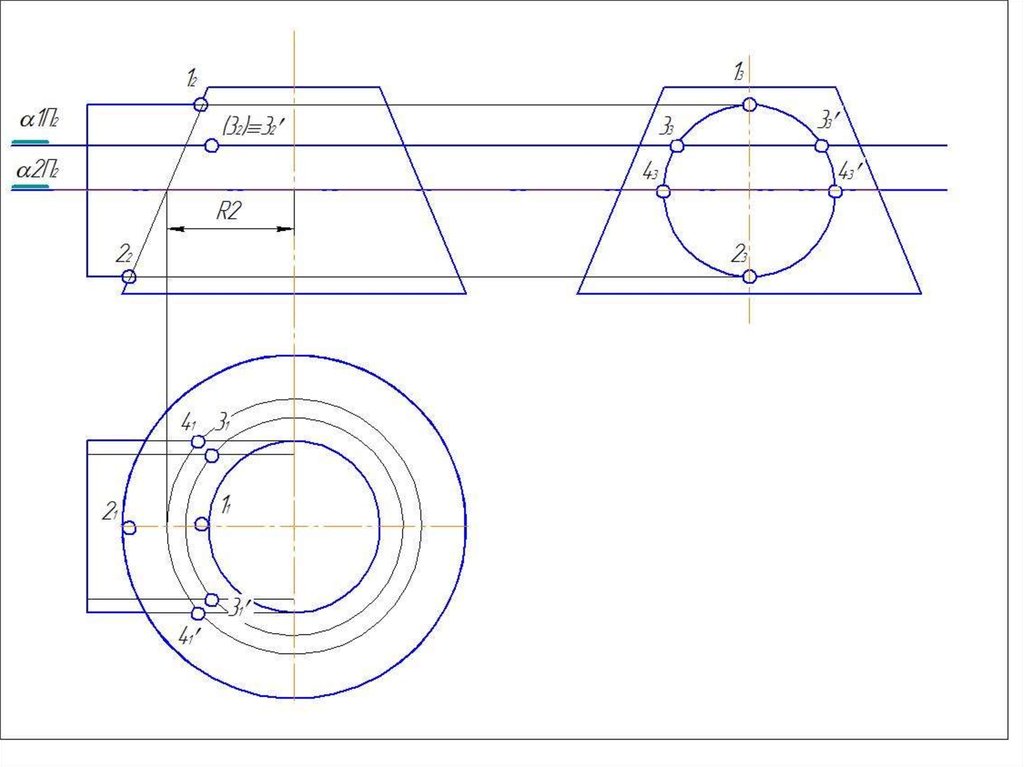
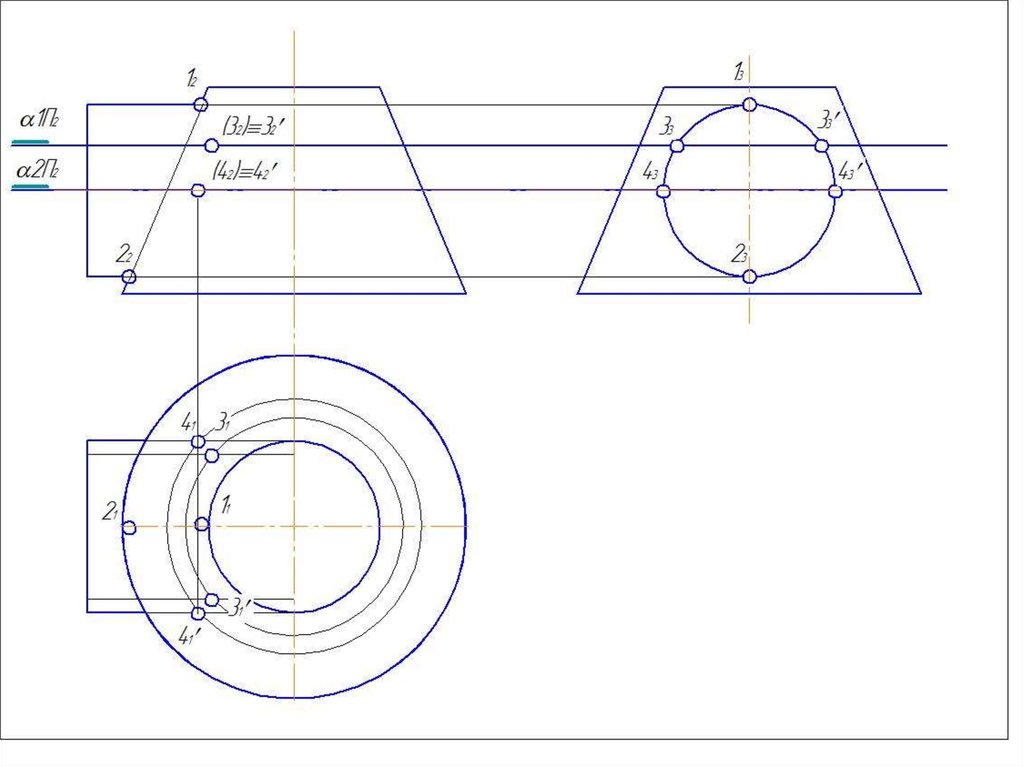
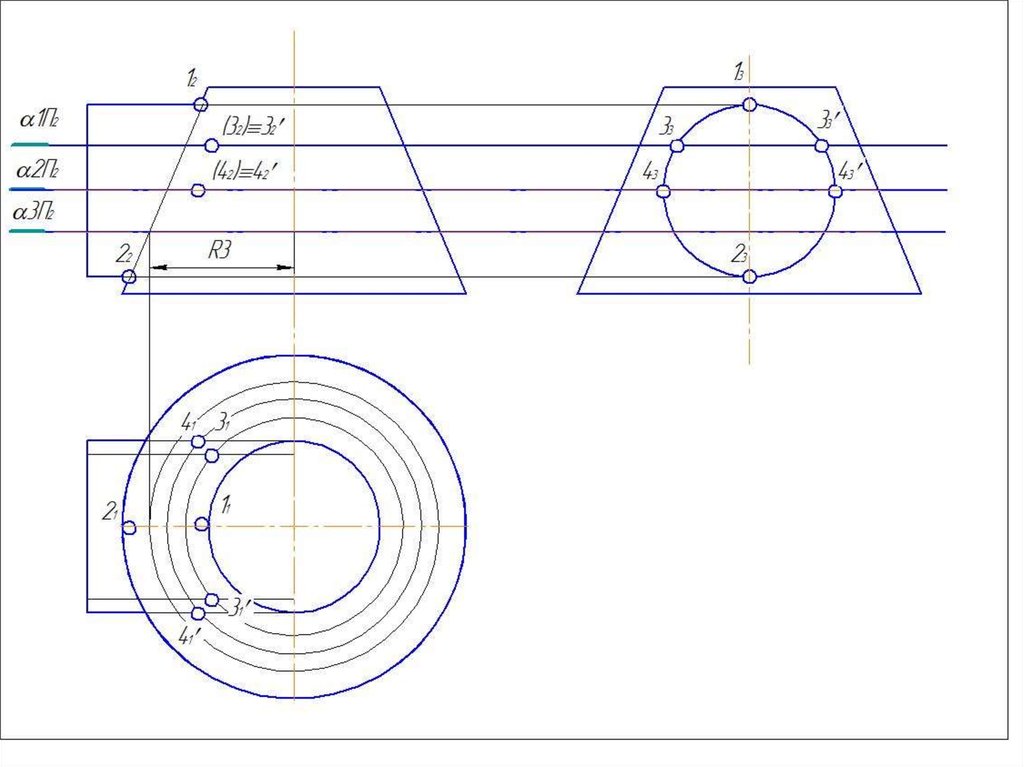
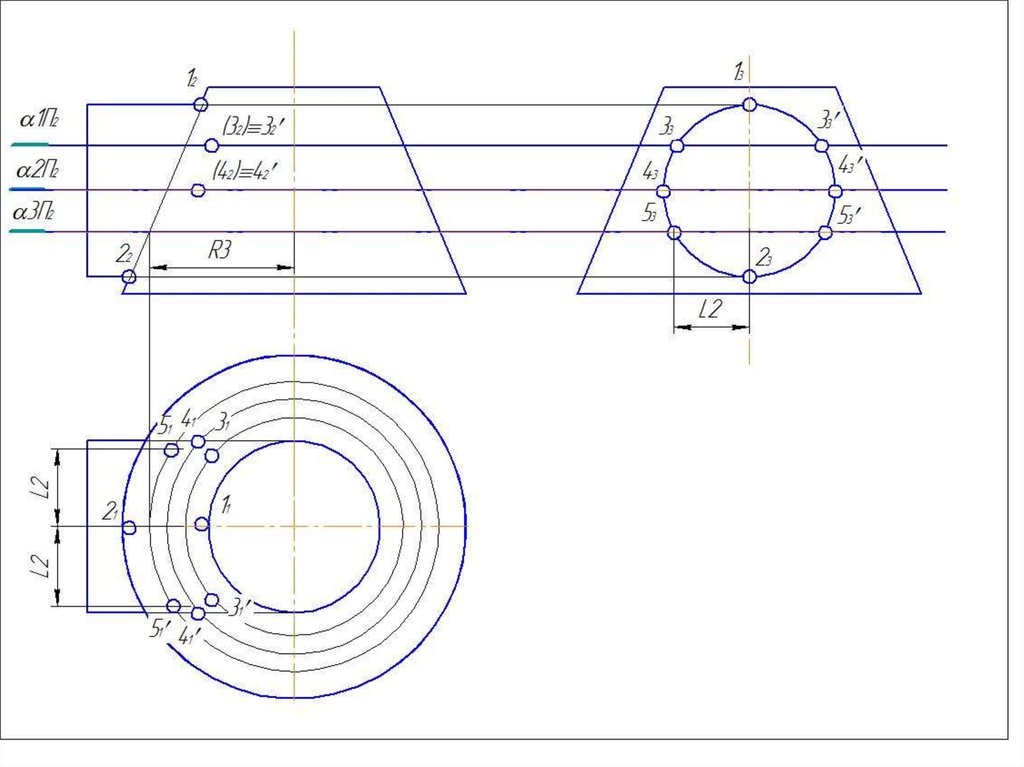
51. Метод вспомогательных концентрических сфер
22262
O22
Rmin
min
422
122
522
72
322
51
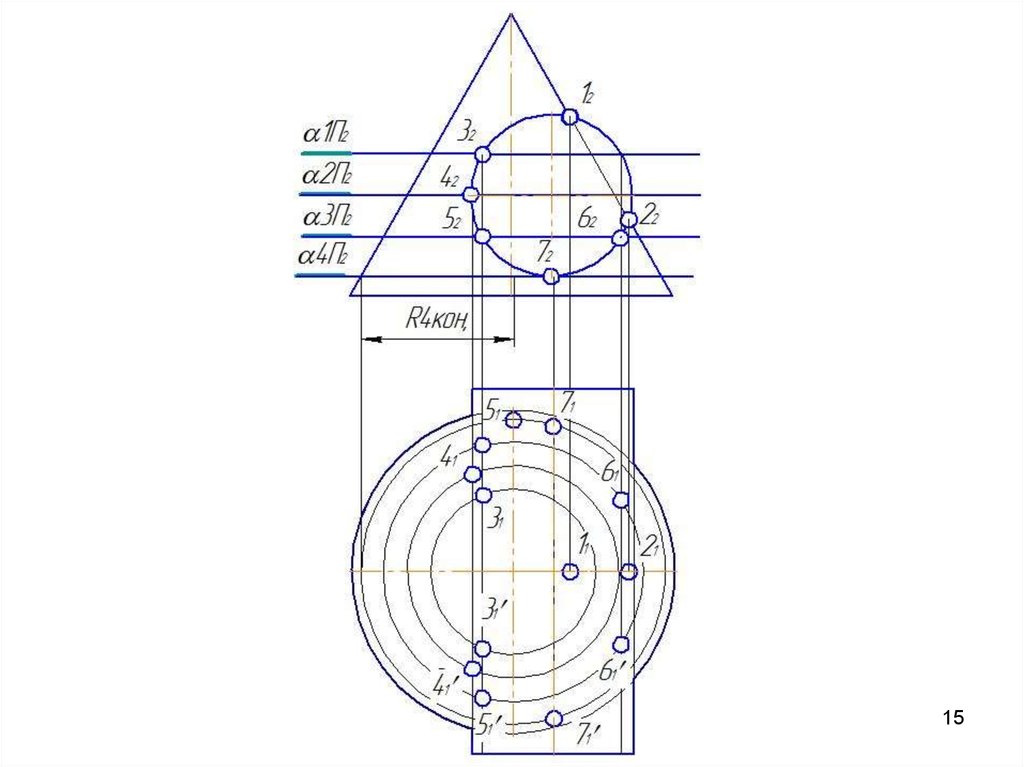
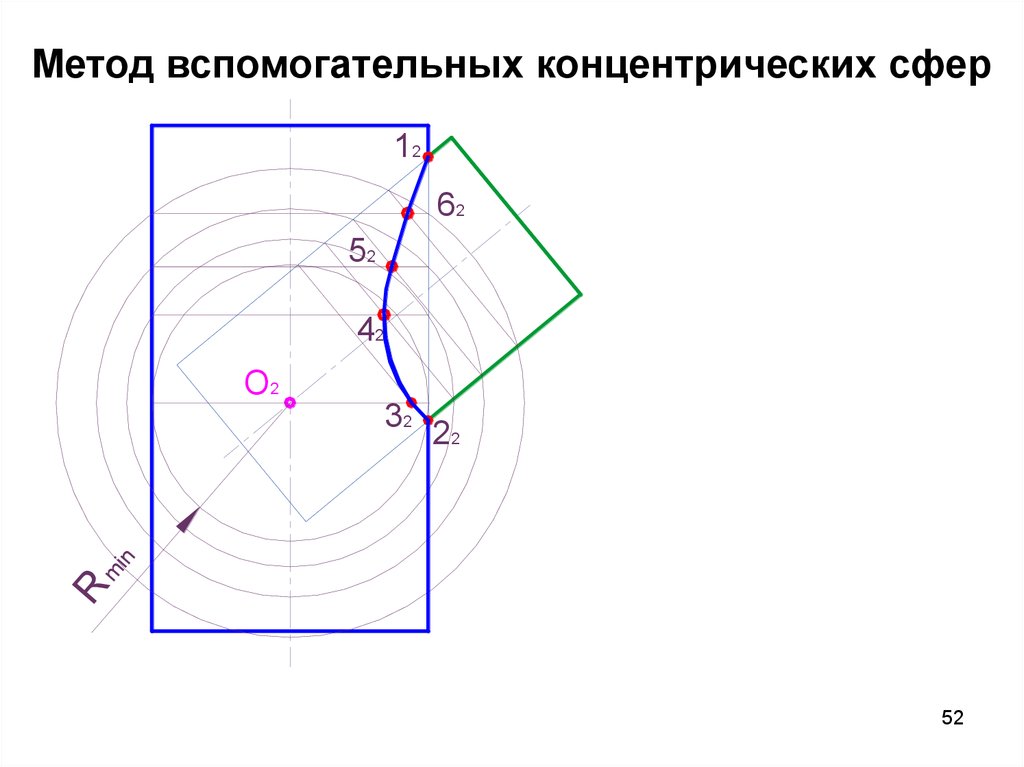
52. Метод вспомогательных концентрических сфер
1262
52
42
32
22
R
m
in
O
O22
52
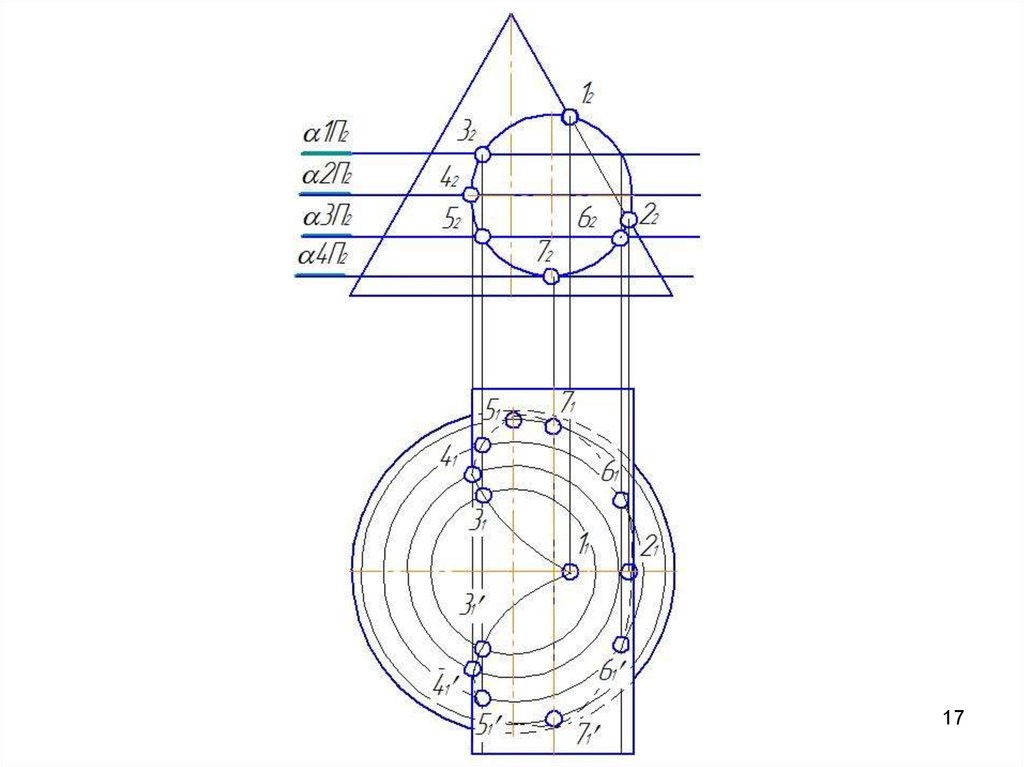
53. ВЫВОДЫ
• Метод концентрических сфер позволяетв одной проекции построить линию
пересечения двух поверхностей.
• Область использования этого метода
ограничена следующими требованиями:
- обе поверхности должны быть
поверхностями вращения;
- их оси должны пересекаться;
- их оси должны лежать в плоскости
параллельной плоскости проекций.
53
54. Контрольные вопросы
1. Какие Вы знаете частные случаипересечения поверхностей вращения?
2. Как строится линия пересечения в
этих случаях?
3. Для чего служит метод
концентрических сфер?
54
55. Контрольные вопросы
4. Достоинства метода концентрическихсфер.
5. Область использования метода.
6. Какой радиус сферы называется
минимальным?
7. Какие точки линии пересечения
являются характерными?
55



























 mathematics
mathematics








