Пересечения поверхностей. Способ вспомогательных сфер. (Лекция 9)

1. Лекция 9. Пересечения поверхностей. Способ вспомогательных сфер

Определить точки пересечения пирамиды прямой а
S
S
a
1
a
2
3
4
1
2
3
4
1
a
4
1
a
S
S
3
2
4
3
2

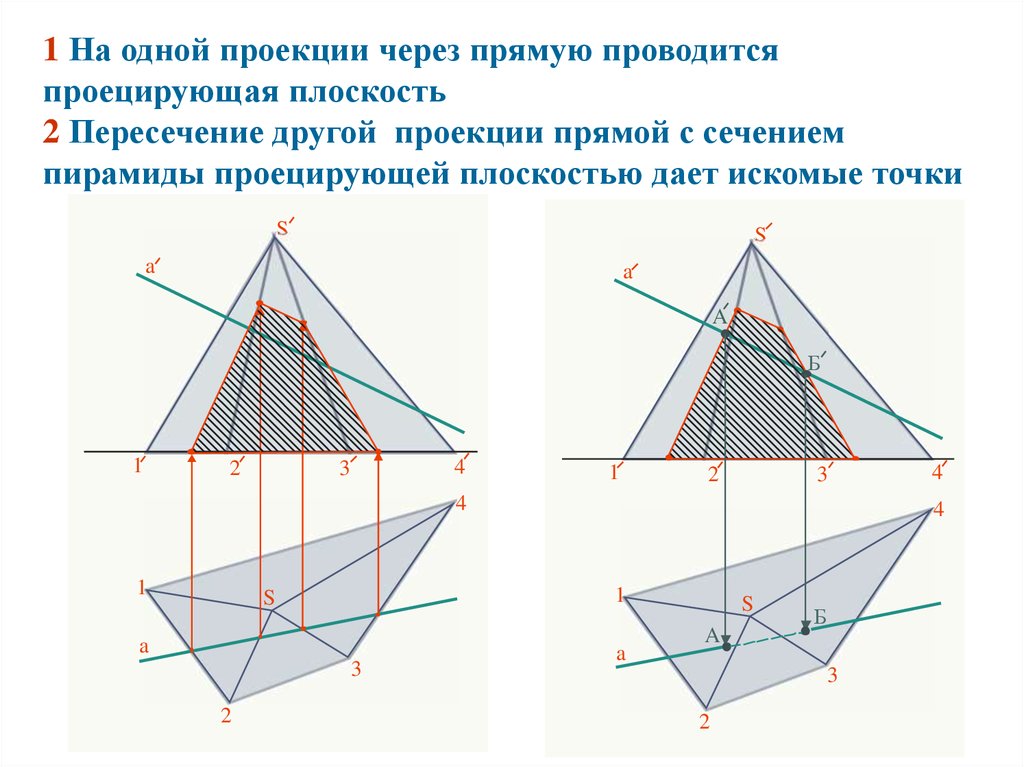
2. 1 На одной проекции через прямую проводится проецирующая плоскость 2 Пересечение другой проекции прямой с сечением пирамиды

проецирующей плоскостью дает искомые точки
S
S
a
a
A
Б
1
2
4
3
1
2
3
4
1
a
3
2
4
1
S
4
a
S
A
Б
3
2

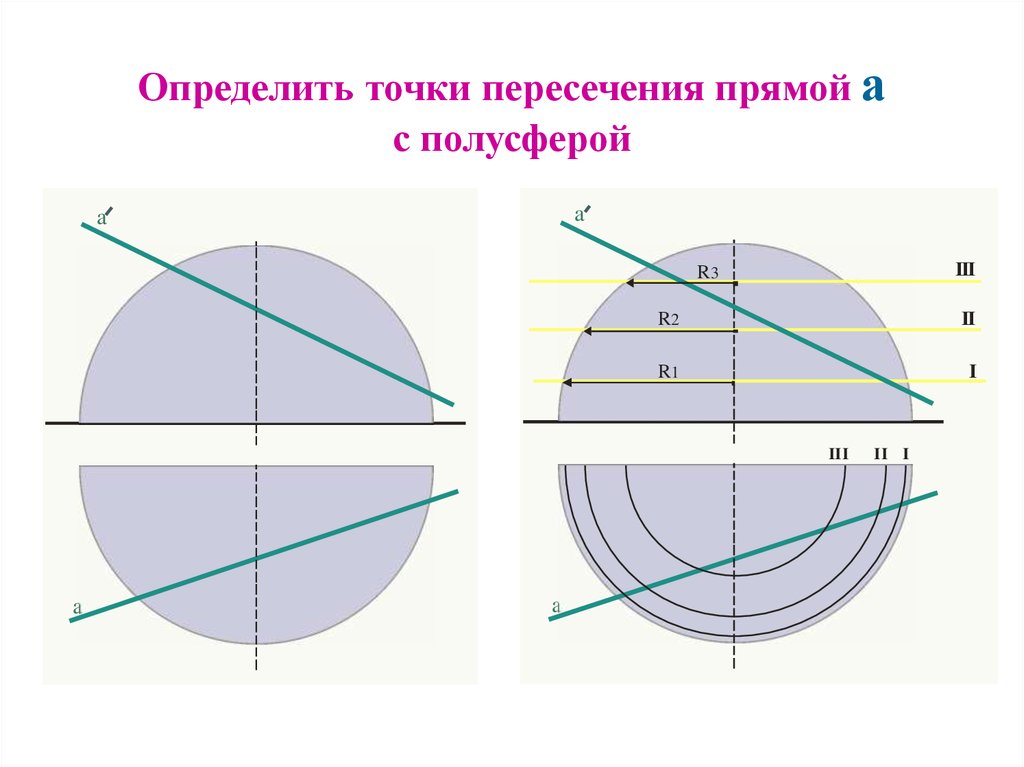
3. Определить точки пересечения прямой а с полусферой

a
a
III
R3
R2
II
R1
I
III
a
a
II I

4. 1 На одной проекции через прямую a проводится проецирующая плоскость 2 Пересечение другой проекции прямой a с сечением

полусферы проецирующей плоскостью дает искомые
точки А и Б
a
a
III
III
A
II
II
I
I II
Б
II I
III
II I
Б
A
a
a
I

5. Пересечение двух тел вращения

Определить линию
пересечения
цилиндра сферой
2
1 Проводим посредник
параллельный фронтальной
плоскости через ось цилиндра
1
1 Точки на контуре
цилиндра
о
2 Экстремальные
точки
3 Промежуточные
точки
I
о
2 Экстремальные точки при
определении линии
пересечения тел вращения с
параллельными осями
вращения лежат в плоскости,
осей вращения

6. Определение экстремальных точек

2
1
о
I
II
2
С помощью посредника II
соединяем на горизонтальной
проекции оси вращения тел через эту прямую проводим
горизонтально-проецирующую
плоскость, в которой будут
лежать экстремальные точки
2
VI
V
IV
1
III
о
II
2
Для определения линии
пересечения сферы
посредником II необходимо
воспользоваться
дополнительными
плоскостями
уровня / III,IV,V, VI/

7. Определение экстремальных точек

2
VI
V
4
2
IV
1
III
о
VI
С помощью
посредниковгоризонтальных
плоскостей уровня
определяем линию
пересечения сферы
посредником II
1
3
о
V
II
IV
III
VI
V
II
IV
III
Точки пересечения
двух сечений
цилиндра и
сферы одной
плоскостьюпосредником
II являются
экстремальными
точками на линии
пересечения
двух тел вращения

8. Промежуточные точки

4
5
VII
6
1
3
о
2
3
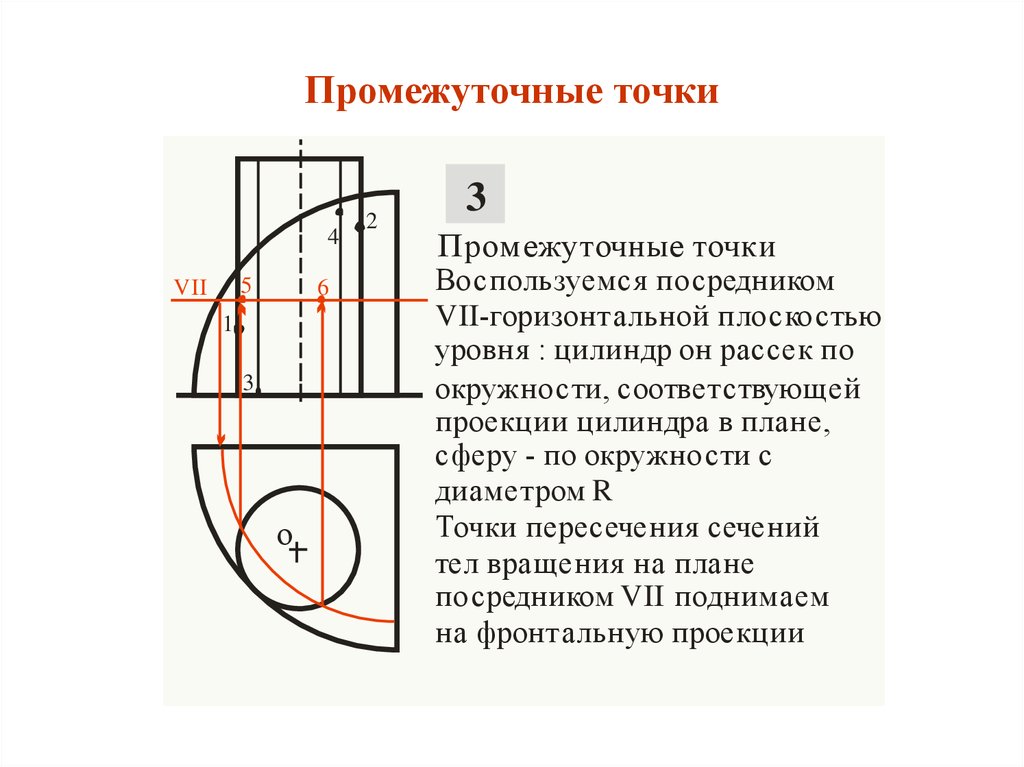
Промежуточные точки
Воспользуемся посредником
VII-горизонтальной плоскостью
уровня : цилиндр он рассек по
окружности, соответствующей
проекции цилиндра в плане,
сферу - по окружности с
диаметром R
Точки пересечения сечений
тел вращения на плане
посредником VII поднимаем
на фронтальную проекции

9. Линия пересечения цилиндра и сферы

4
5
2
4
6
1
5
6
1
3
3
о
о
2

10. Пересечение сферической поверхности с гранной

a
с
б
Определить линию
пересечения сферы трехгранной
призмой
1 Необходимо определить точки
пересечения ребер призмы со сферой
2 Взяв на основании призмы авс
промежуточные точки, провести
через них прямые, параллельные
ребрам и определить точки их
пересечения со сферой
3 Точки пересечения ребер призмы
со сферой соединить через
промежуточные точки плавной линией
с
б
a

11. Использование алгоритма пересечения прямой с поверхностью

a
2
1
3
б
с
1,2,3 - промежуточные
точки на сторонах основания
призмы, через которые на
гранях призмы проводятся
прямые, параллельные
ребрам и находятся
промежуточные точки
пересечения этих прямых
со сферой
2
1
a
б
3
с

12.

a
2
1
3
б
с
Точки пересечения
промежуточных
прямых со сферой
помогают определить
изгиб линии
пересечения
2
1
a
б
3
с

13.

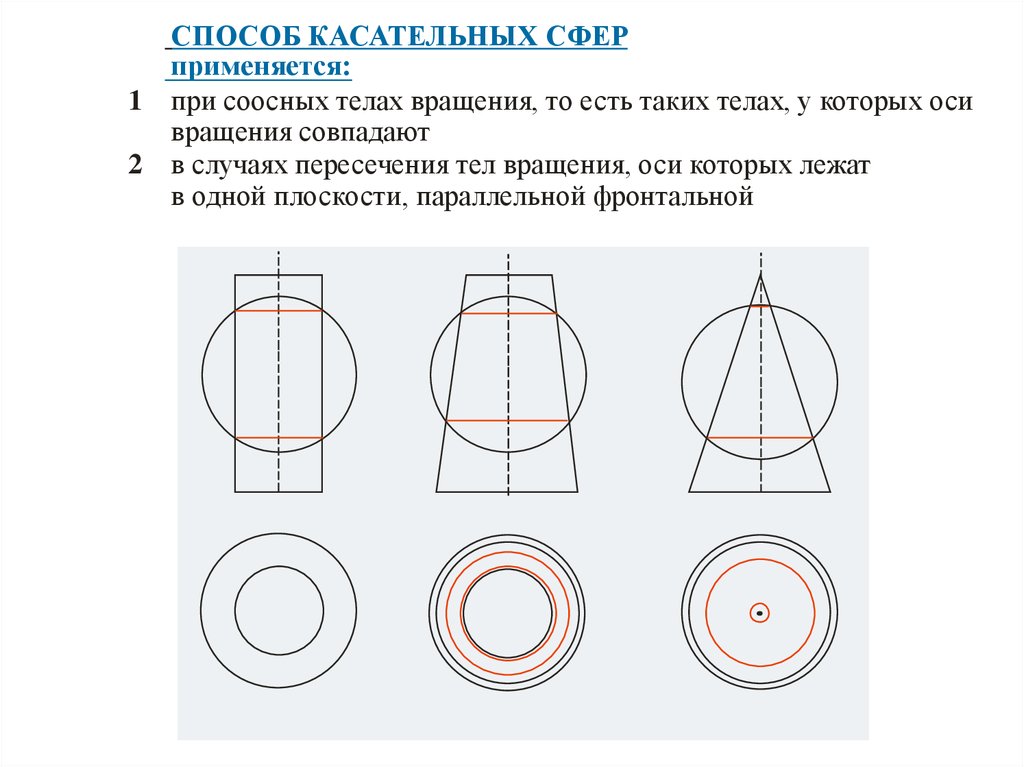
СПОСОБ КАСАТЕЛЬНЫХ СФЕР
применяется:
1 при соосных телах вращения, то есть таких телах, у которых оси
вращения совпадают
2 в случаях пересечения тел вращения, оси которых лежат
в одной плоскости, параллельной фронтальной

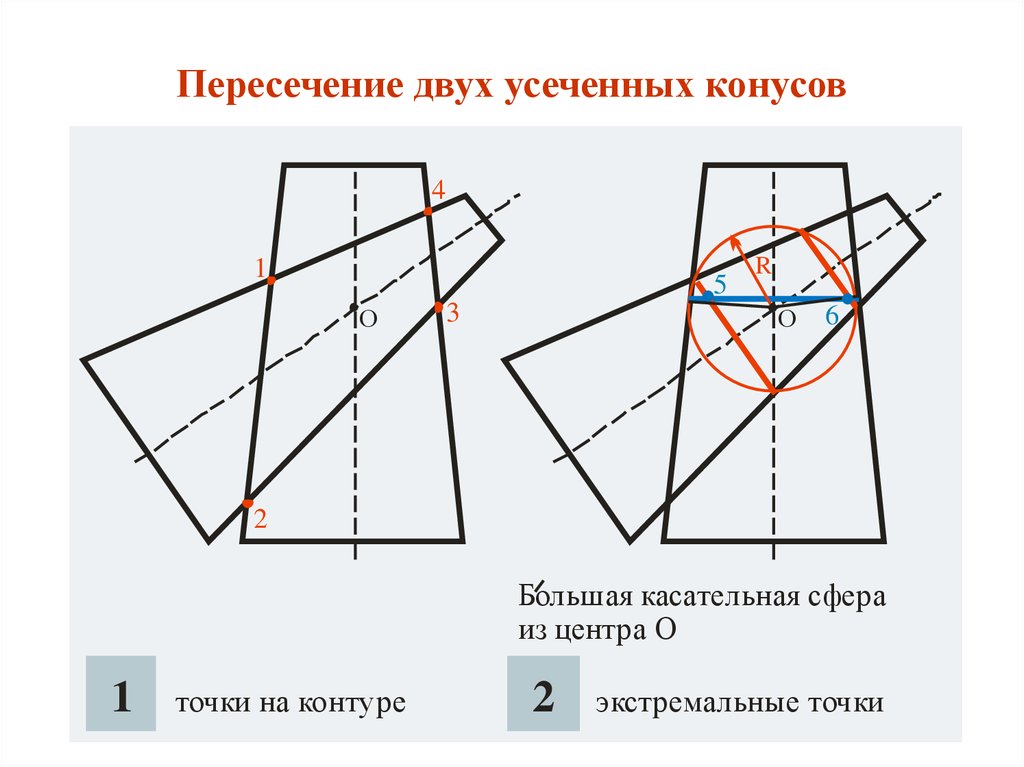
14. Пересечение двух усеченных конусов

4
1
5
О
3
R
О
6
2
Большая касательная сфера
из центра О
1
точки на контуре
2
экстремальные точки

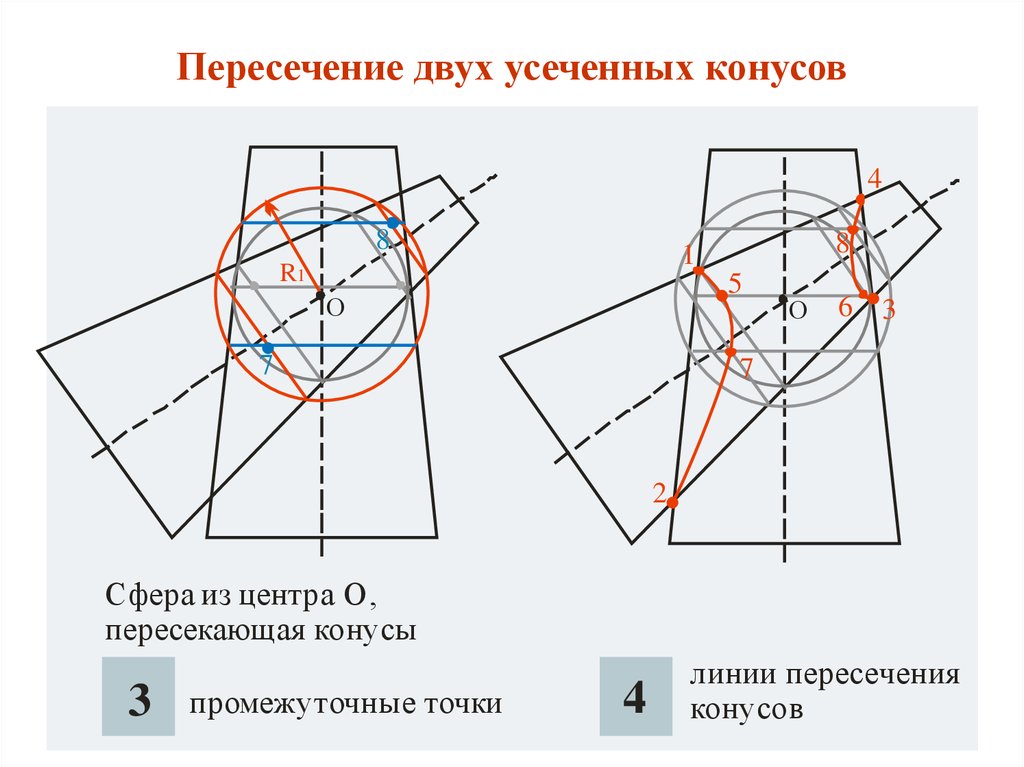
15. Пересечение двух усеченных конусов

4
8
8
1
R1
5
О
7
О
6 3
7
2
Сфера из центра О ,
пересекающая конусы
3
промежуточные точки
4
линии пересечения
конусов

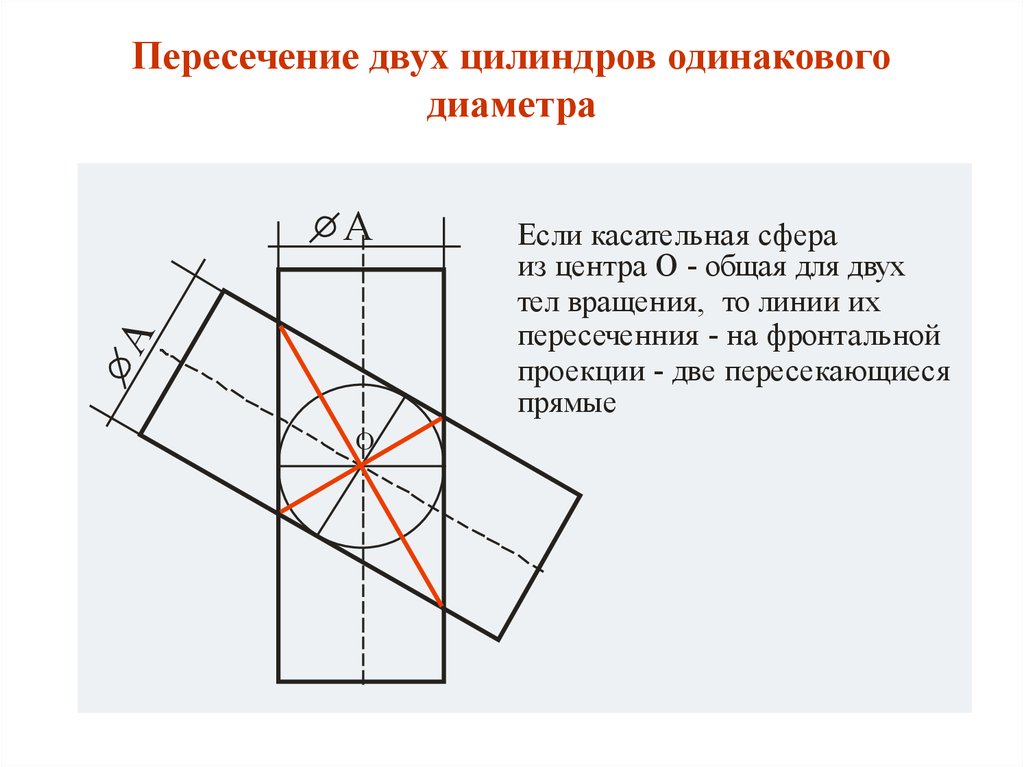
16. Пересечение двух цилиндров одинакового диаметра

А
А
О
Если касательная сфера
из центра О - общая для двух
тел вращения, то линии их
пересеченния - на фронтальной
проекции - две пересекающиеся
прямые

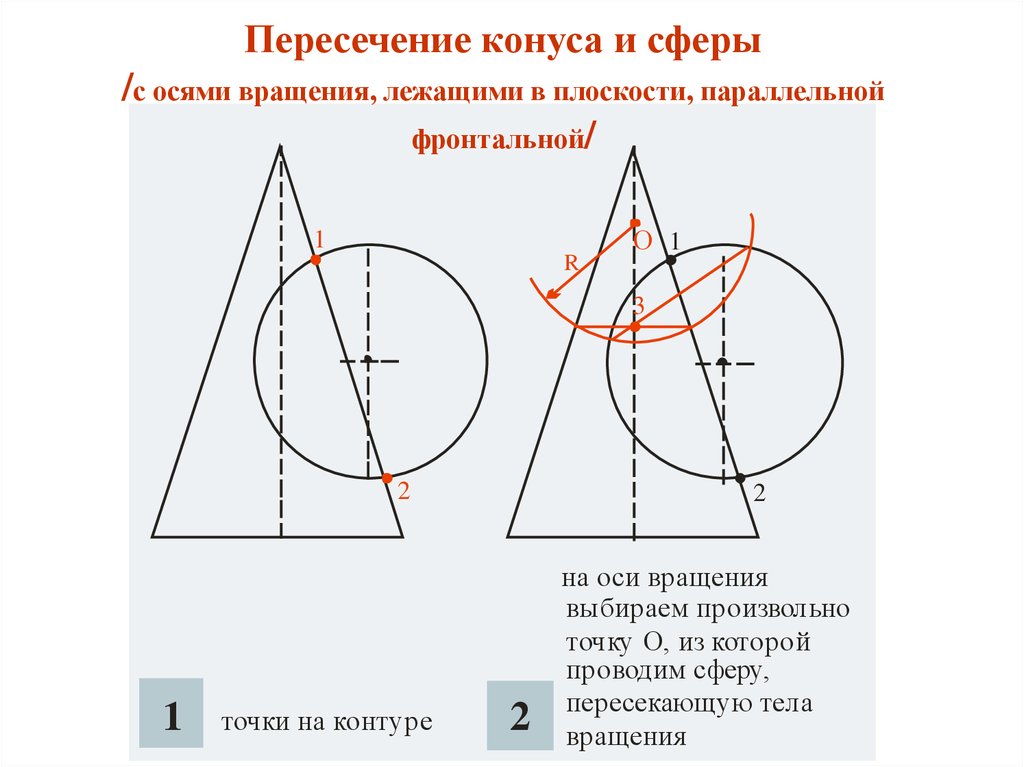
17. Пересечение конуса и сферы /с осями вращения, лежащими в плоскости, параллельной фронтальной/

1
R
О 1
3
2
1
точки на контуре
2
2
на оси вращения
выбираем произвольно
точку О, из которой
проводим сферу,
пересекающую тела
вращения

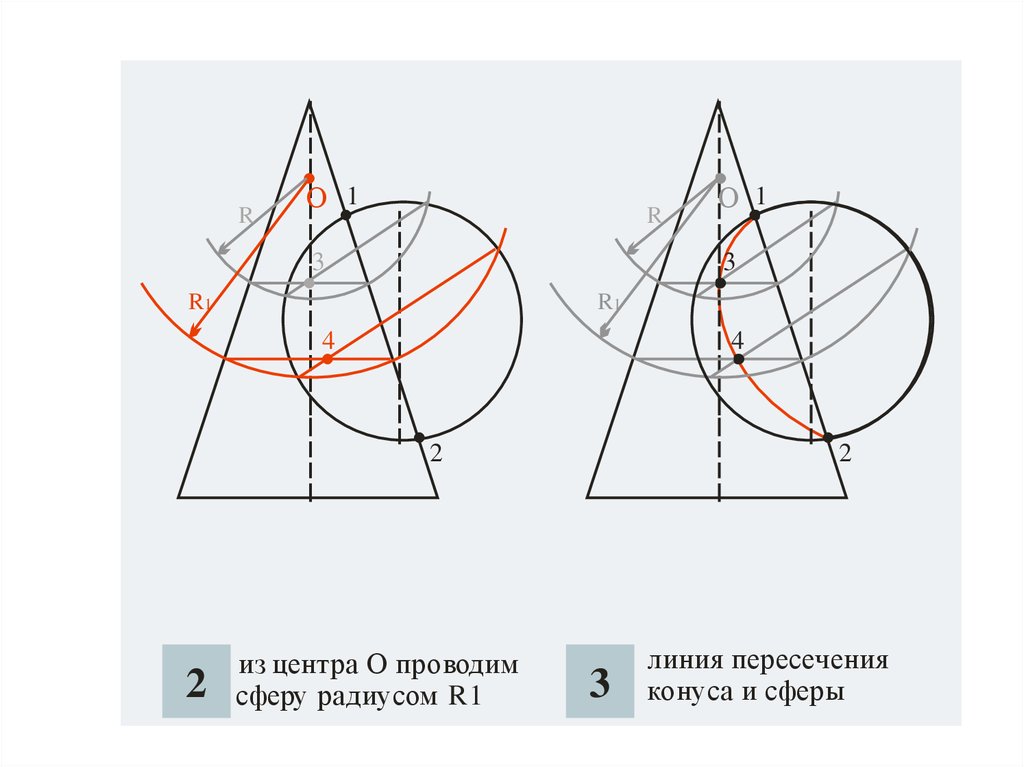
18.

R
О 1
R
3
3
R1
R1
4
4
2
2
О 1
из центра О проводим
сферу радиусом R1
2
3
линия пересечения
конуса и сферы