Similar presentations:
Регрессионный анализ. Эмпирические модели. Понятия регрессии. Уравнение линейной регрессии. (Лекция 9)
1. Лекция 9
Регрессионный анализ2. План лекции:
Эмпирические модели. Понятия регрессии.Уравнение линейной регрессии. Интерпретация
коэффициентов уравнения линейной регрессии.
Эмпирическая линия регрессии: графический,
скользящего среднего. Метод наименьших
квадратов.
Нелинейная
регрессия.
Выбор
формы
функциональной зависимости.
3.
Корреляционную зависимость междупризнаками можно описывать разными
способами. В частности, любая форма связи
может быть выражена уравнением общего вида
y=f(x),
где признак у — зависимая переменная, или
функция от независимой временной X,
называемой аргументом.
4.
Регрессией- называется изменение функции в
зависимости от изменений
одного и нескольких
аргументов
5.
Термин «регрессия»(от лат. regressio—движение назад)
ввел Гальтон.
Изучая статистическим методом наследование количественных
признаков, он обнаружил, что потомство высокорослых и
низкорослых родителей отклоняется регрессирует) от них на 1/3 в
сторону среднего уровня этого признака в данной популяции.
6. Средства, используемые для описания корреляционных связей, составляющие содержание регрессионного анализа:
-Таблицы;
-
Формула;
-
Графики.
7.
Для выражения регрессии служат эмпирические итеоретические ряды, их графики — линии
регрессии, а также корреляционные
уравнения (уравнения регрессии) и коэффициент
линейной регрессии.
8.
Показатели регрессии выражают корреляционнуюсвязь двусторонне, учитывая изменение средней
величины ух признака Y при
изменении значений xi признака X, и, наоборот,
показывают изменение средней величины ху признака X
по измененным значениям yi
признака Y.
9.
10. Уравнение линейной регрессии:
y a bx1 cx2 dx3 .......,где: a, b, с и d — параметры уравнения,
определяющие соотношение между
аргументами и функцией.
11. Уравнение линейной регрессии:
y a bxГде:
а — свободный член;
b – коэффициент регрессии.
12. Схема линий регрессии Y по Х, и Х по Y в системе прямоугольных координат
13.
Параметр а (свободный член регрессии) —графически
представляет
отрезок
ординаты (у) в системе прямоугольных
координат.
Параметр b (коэффициент регрессии) —
угловой
коэффициент,
определяющий
наклон линии регрессии по отношению к
осям координат.
14. Интерпретация параметров регрессии
Параметры bi являются частными коэффициентамикорреляции; (bi)2 интерпретируется как доля
дисперсии Y, объясненная Xi, при закреплении
влияния остальных предикторов, т.е. измеряет
индивидуальный вклад в объяснение Y.
В случае коррелирующих предикторов возникает проблема неопределенности в
оценках, которые становятся зависимыми от порядка включения
предикторов в модель. В таких случаях необходимо применение методов
анализа корреляционного и пошагового регрессионного анализа.
15. Применение регрессионного анализа
Определениеналичия
и
характера
(математического уравнения, описывающего
зависимость) связи между переменными
Определение степени детерминированности
вариации
критеральной
переменной
предикторами
Предсказать значение зависимой переменной с
помощью независимой
Определить вклад независимых переменных в
вариацию зависимой
16. Расчет коэффициентов регрессии, через коэффициент корреляции
byõ r(y
(x
i
i
y)
x)
2
2
bxy r
(x
(y
i
i
x)
2
y)
2
17. Расчет коэффициентов регрессии
byx( y y)( x x)
( x x)
i
i
2
i
byx r
S y iy
S x ix
bxy
( y y)( x x)
( y y)
i
i
2
i
S xix
bxy r
S yiy
18. Для группирируемых выборок
byxp
xy
xy
( px x)( p y y )
n
2
(
p
x
)
x
2
p
x
x
n
bxy
p
xy
xy
( px x)( p y y )
2
p
y
y
n
( p y y ) 2
n
19. Параметры уравнения линейной регрессии:
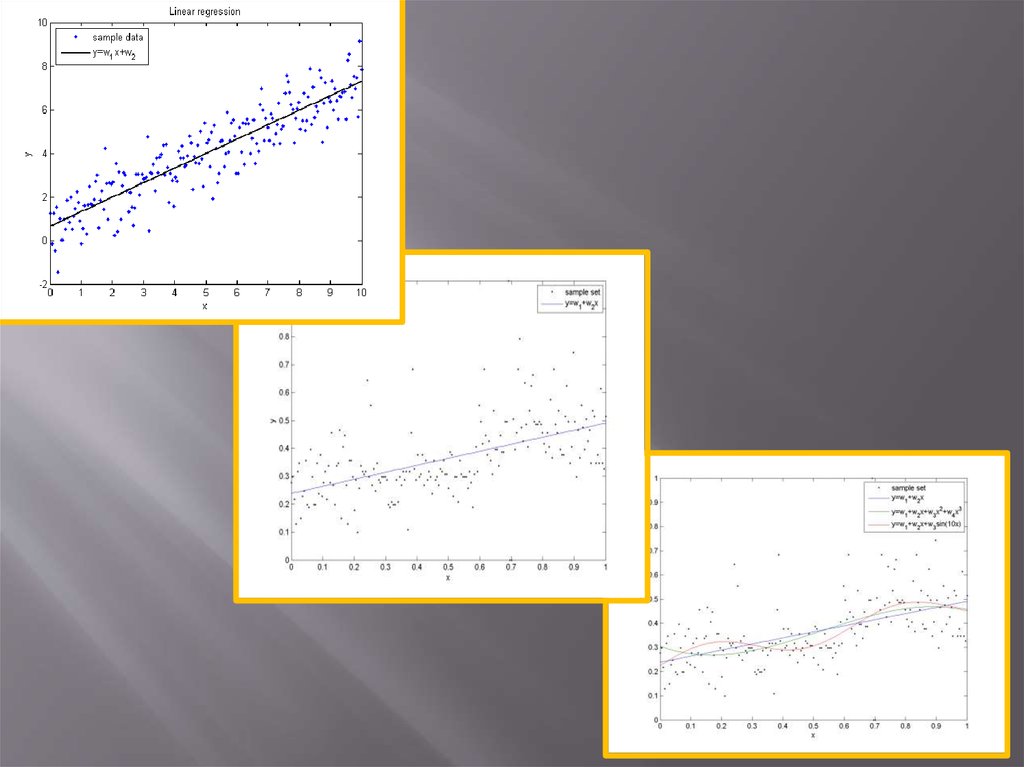
Определение параметров линейной регрессии —одна из задач регрессионного анализа. Она
решается способом наименьших квадратов,
основанным на требовании, чтобы сумма
квадратов отклонений вариант от линии
регрессии была наименьшей. Этому требованию
удовлетворяет следующая система
нормальных уравнений:
20. Параметры уравнения линейной регрессии:
21.
Ряды регрессии — это ряды усредненных значений(ух и ху) варьирующих признаков Y и X,
соответствующих значениям аргументов yi и xi
22.
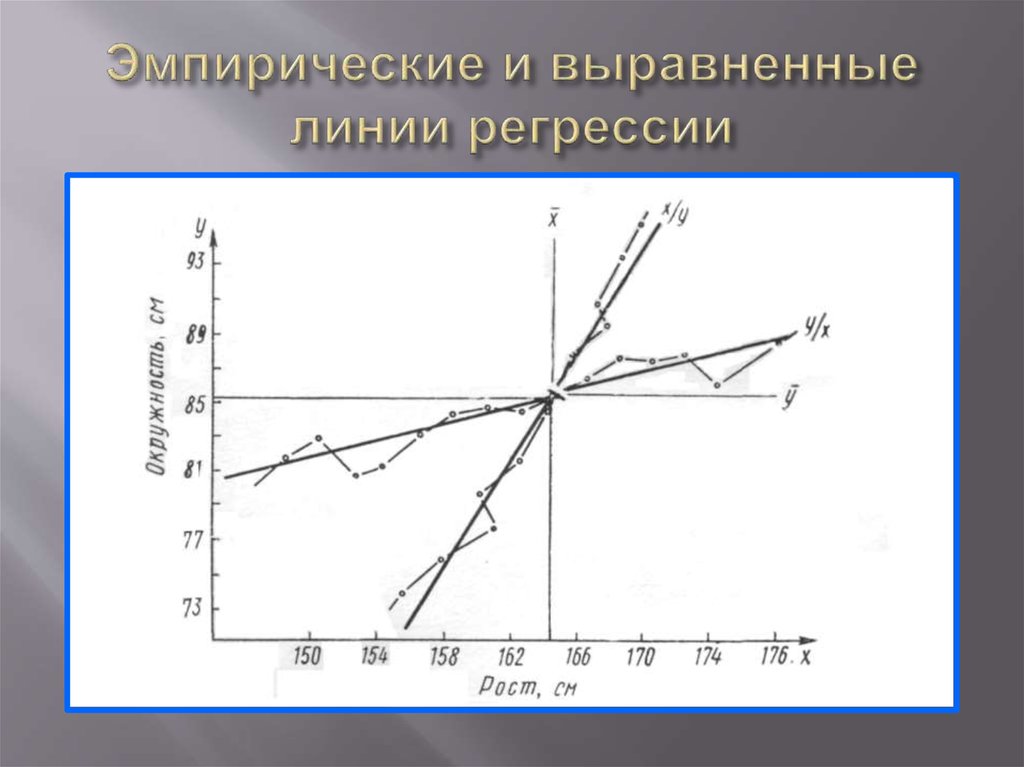
Выравниванием эмпирических линии регрессии называется замена ломаных линий регрессиина плавно идущие в системе
прямоугольных координат.
23. Эмпирические и выравненные линии регрессии
24. Способы выравнивания эмпирических рядов регрессии:
ГрафическийСпособ скользящей средней
Способ наименьших квадратов
25. Графический способ выравнивания
Наиболее простой способ, не требующийвычислительной работы.
Эмпирический ряд регрессии изображается в виде
линейного графика в системе прямоугольных
координат. Затем на глаз определяются
серединные точки регрессии, но которым с
помощью линейки или лекала проводится
сплошная линия.
Недостаток способа: он не исключает влияние на результаты выравнивания
регрессии индивидуальных свойств исследователя. Поэтому в тех
случаях, когда необходима более высокая точность при замене
ломаных линий регрессии на плавно идущие, пользуются другими
способами выравнивания эмпирических рядов.
26. Способ скользящей средней
Сводится к последовательному вычислению рядасредних
арифметических
из двух, трех
соседних членов эмпирического ряда регрессии.
Он удобен особенно в тех случаях, когда эмпирический ряд представлен
достаточно большим числом членов, так что потеря двух из них
(крайних), что неизбежно при этом способе выравнивания, заметно не
отразится на его структуре.
27. способ наименьших квадратов
Предложен в 1806 году К. Гауссом и независимо от негоА. Лежандром.
Наиболее точный из всех способов выравнивания
эмпирических рядов.
В основу положена теорема, согласно которой сумма
квадратов отклонений вариант (xi) от средней
арифметической (х) есть величина наименьшая, т.е.
∑(хi-x)=min.
Метод нашел широкое применение не только в
биологии, но и в технике.
28. Метод наименьших квадратов сводится к решению следующих задач:
ПО ГЕОМЕТРИЧЕСКОМУ МЕСТУ ТОЧЕК ДВУХ ПЕРЕМЕННЫХ В СИСТЕМЕ ПРЯМОУГОЛЬНЫХКООРДИНАТ ПОДБИРАЮТ МАТЕМАТИЧЕСКИЕ УРАВНЕНИЕ, НАИЛУЧШИМ ОБРАЗОМ ОТОБРАЖАЮЩЕЕ
ФОРМУ СВЯЗИ МЕЖДУ ЭТИМИ ВЕЛИЧИНАМИ.
ПОДСТАВЛЯЯ В ИСКОМОЕ УРАВНЕНИЕ СООТВЕТСТВУЮЩИЕ ЭМПИРИЧЕСКИЕ ДАННЫЕ, ОБРАЗУЮТ
СИСТЕМУ НОРМАЛЬНЫХ УРАВНЕНИЙ, РЕШАЯ КОТОРУЮ НАХОДЯТ ПАРАМЕТРЫ ЭТОГО УРАВНЕНИЯ.
ПОДСТАВЛЯЯ ПАРАМЕТРЫ В ОБЩЕЕ УРАВНЕНИЕ, ПОЛУЧАЮТ ЭМПИРИЧЕСКОЕ УРАВНЕНИЕ РЕГРЕССИИ,
ВЫРАЖАЮЩЕЕ ЗАВИСИМОСТЬ МЕЖДУ ПЕРЕМЕННЫМИ ВЕЛИЧИНАМИ Y И X.
ПОДСТАВЛЯЯ В ЭМПИРИЧЕСКОЕ УРАВНЕНИЕ ЗНАЧЕНИЕ ОДНОЙ ПЕРЕМЕННОЙ (X), НАХОДЯТ
СООТВЕТСТВУЮЩИЕ СРЕДНИЕ ЗНАЧЕНИЯ ДРУГОЙ ПЕРЕМЕННОЙ (УХ). ПОЛУЧАЕТСЯ РЯД ТЕОРЕТИЧЕСКИ
ОЖИДАЕМЫХ (ВЫРАВНЕННЫХ) ЗНАЧЕНИЙ ФУНКЦИИ ПО ИЗВЕСТНЫМ ЗНАЧЕНИЯМ АРГУМЕНТА.
РАССЧИТАННЫЕ ПО ЭТИМ УРАВНЕНИЯМ ЗНАЧЕНИЯ УХ И ХУ ИЗОБРАЖАЮТ В ВИДЕ ВЫРАВНЕННЫХ ЛИНИЙ
РЕГРЕССИИ Y ПО X И X ПО Y.
29. Оценка достоверности показателей регрессии осуществляется по формулам:
sbyx( yi y )( xi x)
2
(
y
y
)
i
2
(
x
x
)
i
2
(n 2) ( xi x) 2
sbxy
( yi y )( xi x)
2
(
y
y
)
i
2
(
y
y
)
i
(n 2) ( yi y ) 2
2
30.
Временные ряды, или ряды динамики,показывающие изменение признаков во времени.
Регрессия таких рядов является односторонней.
31. Тест по теме:
«Регрессионныйанализ»
32. Уравнение линейной регрессии имеет вид:
ya
bx
y a bx
y ab x
y
a b
x
33. Изменение функции в зависимости от изменения одного или нескольких аргументов называется …
дисперсиейсессией
регрессией
дипрессией
34. Укажите неправильный вариант ответа. Замена ломаных линий регрессии на плавно идущие в системе прямоугольных координат может
способомпрямоугольника
латинского
графическим способом
способом
наименьших
квадратов
способом скользящей средней
35. Что показывают коэффициенты регрессии в уравнении множественной регрессии?
зависимость между переменными случайной величинызависимость переменной y от одного из признаков x1, x2
размерность независимых переменных
нет правильного варианта
36. Ряды регрессии – это …
ряды усредненных значений (yx и xy)варьирующих признаков y и x
соответствующих значениям аргументов yi и xi
система уравнений для определения значений
у и х при составлении уравнения регрессии
ряды динамики переменных х и y
другой вариант ответа
37.
38. Формула описывающая коэффициент корреляции в генеральных совокупностях X и Y
а)r
б)
в)
x
i
x ( yi y )
( n 1) S x S y
cov x, y
x
y
r
г) другой вариант ответа
39. Формула для расчета оценки непараметрического коэффициента корреляции Спирмена
6 d i 2а)
rs 1
б)
в)
r
N ( N 2 1)
Cxy
C2 x C2 y
другой вариант ответа
г)
tô
r
N 2
1 r2
40. Как оценивается статистическая значимость коэффициента корреляции?
а)б)
в)
г)
H0 : 0
H0 : 0
H0 : 0
H0 : 0








































 mathematics
mathematics








