Уравнение переноса излучения

1. Уравнение переноса излучения

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
[email protected]

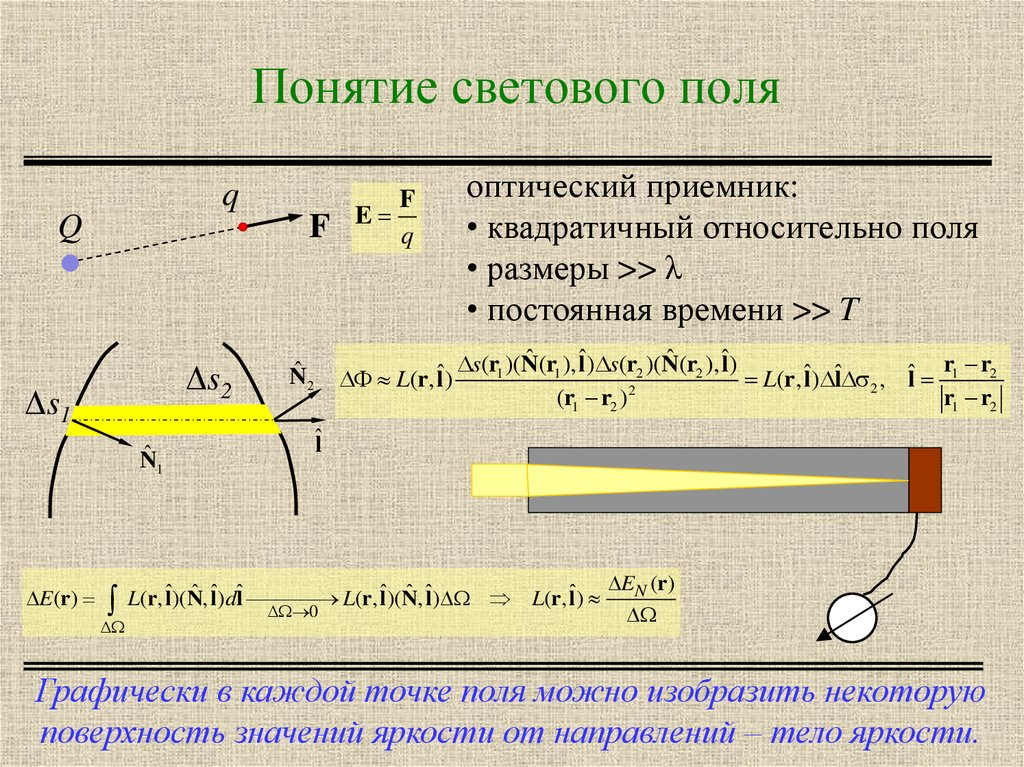
2. Понятие светового поля

q
Q
F
Δs2
Δs1
ˆ
N
1
E (r)
F
E
q
оптический приемник:
• квадратичный относительно поля
• размеры >> λ
• постоянная времени >> T
ˆ (r ), ˆl ) s(r )(N
ˆ (r ), ˆl )
s(r1 )(N
1
2
2
ˆ
ˆl ) ˆl , ˆl r1 r2
L(r, l )
L
(
r
,
2
(r1 r2 )2
r1 r2
ˆ
N
2
ˆl
ˆ , ˆl )dˆl
ˆ , ˆl ) L(r, ˆl ) EN (r)
L(r, ˆl )(N
L(r, ˆl )(N
0
Графически в каждой точке поля можно изобразить некоторую
поверхность значений яркости от направлений – тело яркости.

3. Интегральные характеристики поля

ˆ , ˆl )dˆl E (r)
L(r, ˆl )(N
ˆ ,ˆl ) 0
(N
ˆ , ˆl )dˆl
L(r, ˆl )(N
ˆ , ˆl ) 0
(N
Поток мощности излучения через произвольную единичную площадку:
H (r )
ˆ , ˆl )dˆl
L(r, ˆl )(N
ˆ , ˆl ) 0
(N
ˆ , ˆl )dˆl
L(r, ˆl )(N
ˆ ,ˆl ) 0
(N
L(r, ˆl)(Nˆ , ˆl)dˆl Nˆ , L(r, ˆl)ˆldˆl E(r) L(r, ˆl)ˆldˆl
Однако реакция произвольного объемного приемника будет определяться
другой величиной – плотностью энергии светового поля:
N
(S)
ˆ , ˆl )dSdˆl l ,
dW L(r, ˆl )(N
c
(r)
ˆ , ˆl )dS
dV l (N
dW 1
L(r, ˆl )dˆl E0 (r)
dV c
l
(V)
L(r, ˆl)dˆl
l
поле состоит из лучей, мощность, текущая по каждому из
которых, и есть яркость

4. Световое поле в мутной среде

ˆl
εdl – вероятность столкновения на участке
траектории длины dl;
σdl – вероятность рассеяния на участке
траектории длины dl;
κdl – вероятность поглощения на участке
траектории длины dl;
1 ˆˆ
x(l, l ) – вероятность рассеяния под
4
определенным углом.
ˆl
d
ˆl, ˆl ) L(r, ˆl )dˆl dl Q(r, ˆl )dl
ˆ
dL Ldl
x
(
(l, ),
4
dl
ˆ
ˆ
ˆl, ˆl ) L(r, ˆl )dˆl Q(r, ˆl )
(l, ) L(r, l ) L
x
(
4
Феноменологический вывод уравнения переноса излучения (УПИ)

5. Закон Bouguer

Допустим, что среда чисто поглощающая: =0 и без источников
собственного излучения. Тогда УПИ примет вид
(ˆl, ) L(r, ˆl ) (r) L(r, ˆl )
r r0 ˆl
dL(r0 ˆl, ˆl )
(r0 ˆl ) L(r0 ˆl , ˆl )
d
ˆ
ˆ
ˆ
ˆ
L(r0 l , l ) L(r0 , l )exp (r0 l ) d
0
ˆl, ˆl )
L
(
r
0
( ) (r0 ˆl )d T ( , ˆl )
exp ( )
ˆ
L(r , l )
0
0
показатели ослабления, рассеяния, поглощения – входят в
выражения под экспонентой с размерностью 1/м

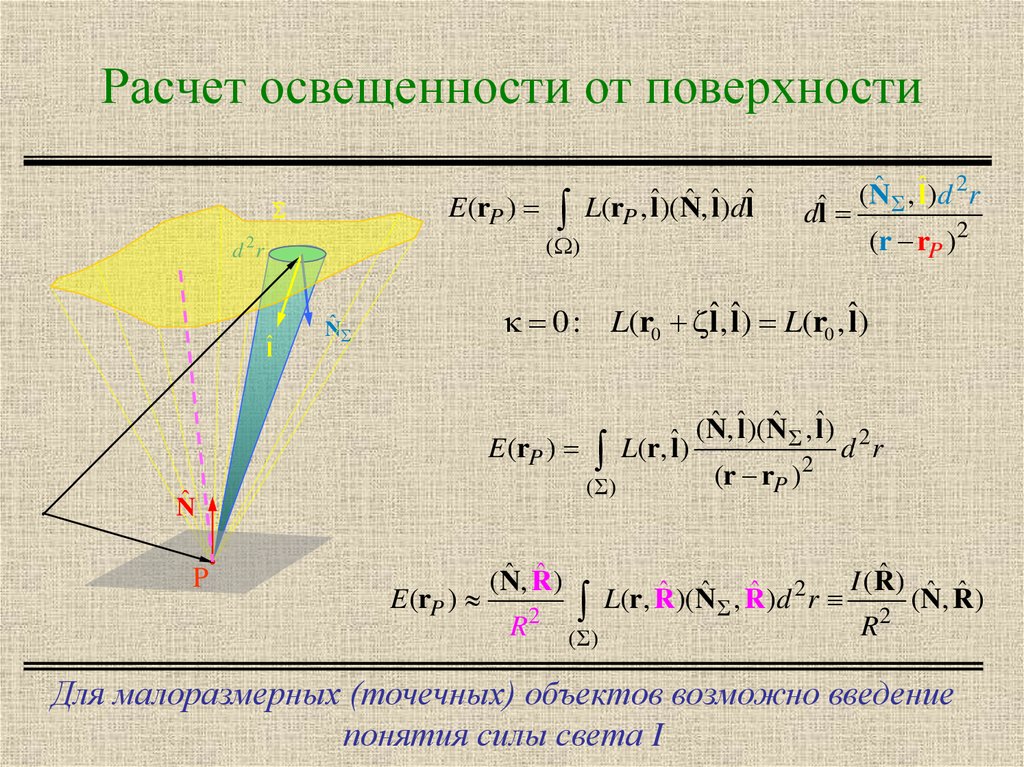
6. Расчет освещенности от поверхности

E (rP )
dˆl
ˆ , ˆl )d 2 r
(N
( )
2
d r
ˆl
(r rP )2
0 : L(r0 ˆl, ˆl ) L(r0 , ˆl )
ˆ
N
ˆ , ˆl )(N
ˆ , ˆl ) 2
(
N
E (rP ) L(r, ˆl )
d r
2
(r rP )
( )
ˆ
N
P
ˆ , ˆl )dˆl
L(rP , ˆl )(N
E (rP )
ˆ ,R
ˆ)
(N
R2
ˆ)
I (R
2
ˆ
ˆ
ˆ
L(r, R)(N , R)d r R2 (Nˆ , Rˆ )
( )
Для малоразмерных (точечных) объектов возможно введение
понятия силы света I

7. Уравнение Гершуна-Гуревича-Kubelka-Munk

Проинтегрируем почленно УПИ по полному телесному углу:
1.
2.
L(r, ˆl)dˆl E0 (r),
ˆl )dˆl E изл (r)
Q
(
r
,
0
1
x(ˆl, ˆl ) L(r, ˆl )dˆl dˆl
4
ˆl ) 1 x(ˆl, ˆl )dˆl dˆl L(r, ˆl )dˆl E (r)
L
(
r
,
0
4
1
3.
(ˆl, )L(r, ˆl)dˆl , L(r, ˆl)ˆldˆl , E(r) div E(r)
div E(r) (r) E0 (r) Eoизл (r)
В уравнении заключена вся теория красок

8. Закон Bouguer-Allard

Рассмотрим точечный источник в чисто поглощающей среде. Из
симметрии задачи нетрудно отметить:
1 d 2
r
2
r dr
0
I0
изл
E0 (r) 0 (r)
(r ) 2 (r )
2
4 r
r
I0
1 d 2
2
r
E
(
r
)
(
r
)
E
(
r
)
(
r
),
(
r
)
E
(
r
)
r
r 2 dr
r2
d
(r ) (r ) (r ) I 0 (r )
dr
r
r
I0
r
1
E (r ) 2 I 0 exp ( )d d C0 exp ( )d 2 exp ( )d
r
0
0
r
0
0
E(r ) E0 (r ) E (r ), div
Облученность в поглощающей среде убывает экспоненциально
и пропорционально обратному квадрату расстояния