Уравнение глобального освещения

1. Уравнение глобального освещения

Будак Владимир Павлович,
НИУ «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
[email protected]

2. Фотореалистическое изображение

Компьютерная графика – визуализация распределения яркости объектов
в трехмерном пространстве

3. Яркость объекта при глобальном освещении

1
ˆ , ˆl ) dˆl
L(r, ˆl ) L0 (r, ˆl ) L(r, ˆl ) (r; ˆl , ˆl ) (N
(4 )
(r; ˆl , ˆl )
(ˆl )
– коэффициент яркости при направленном освещении
BRDF (Bidirectional Reflectance Distribution Function)
в литературе по теплотехнике и компьютерной графике
Описание отражения в фотометрии

4. Коэффициент отражения и коэффициент яркости

Коэффициент отражения ρ определяется (МСС, 20-040) как отношение
отраженного потока Fr к упавшему Fi:
Fr
Fi
Коэффициент яркости b определяется (МСС, 20-200) как отношение яркости
Lr (ˆl )
ˆ
отраженного излучения в данном направлении объекта к яркости идеальной b( l )
Ld
диффузной пластины, находящейся в тех же условиях освещения:
Lr (ˆl )
Lr (ˆl )
* ˆ
ˆ
ˆ
ˆ
b ( l )
r (l ), b( l 0 , l )
Ld
Ld
1
ˆ
ˆ , ˆl ) dˆl
Lr (r, l )
b(r; ˆl , ˆl ) Li (r, ˆl )(N
( Nˆ , ˆl ) 0
1
ˆ , ˆl ) dl 1, (ˆl , ˆl ) ( ˆl, ˆl )
b(r; ˆl , ˆl ) (r; ˆl , ˆl ) r * (r, ˆl ) p(r; ˆl , ˆl ),
p(r; ˆl, ˆl )( N
Аналогично вводится и коэффициент яркости при направленнодиффузном отражении (ˆl , ˆl )

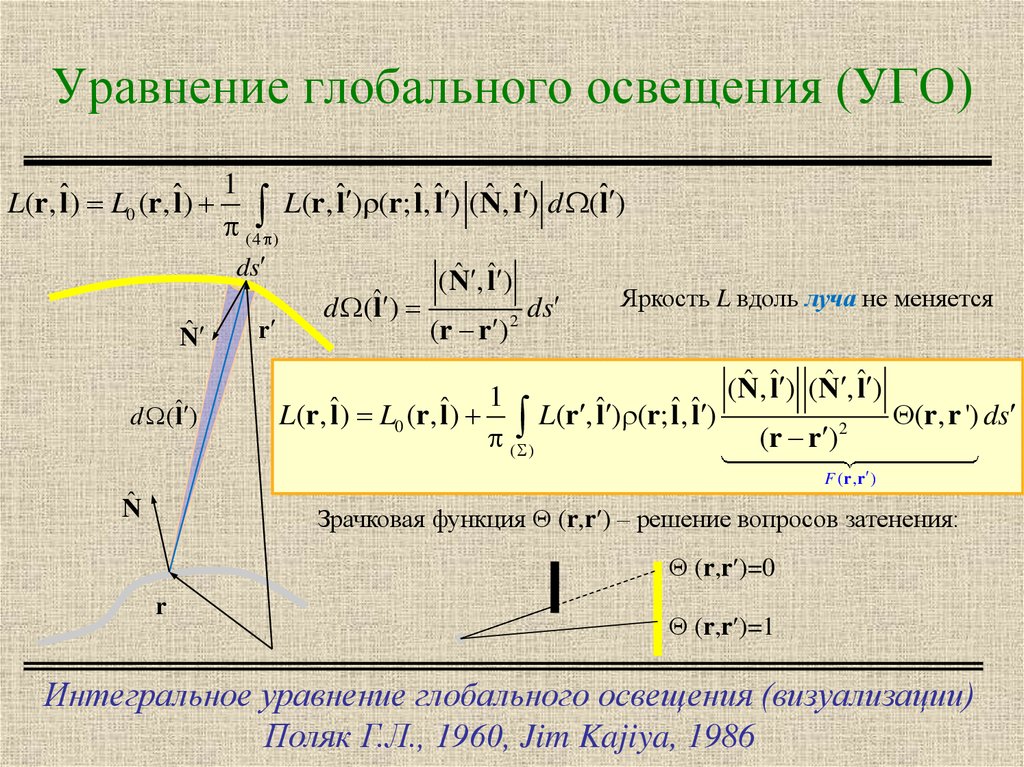
5. Уравнение глобального освещения (УГО)

1
ˆ , ˆl ) d (ˆl )
L(r, ˆl ) L0 (r, ˆl ) L(r, ˆl ) (r; ˆl, ˆl ) (N
(4 )
ds
ˆ
N
d (ˆl )
r
d (ˆl )
ˆ , ˆl )
(N
(r r ) 2
ds
Яркость L вдоль луча не меняется
ˆ , ˆl ) (N
ˆ , ˆl )
(N
1
L(r, ˆl ) L0 (r, ˆl ) L(r , ˆl ) (r; ˆl, ˆl )
(r, r ') ds
2
( )
(r r )
F ( r ,r )
ˆ
N
Зрачковая функция (r,r ) – решение вопросов затенения:
(r,r )=0
r
(r,r )=1
Интегральное уравнение глобального освещения (визуализации)
Поляк Г.Л., 1960, Jim Kajiya, 1986

6. УГО как краевая задача УПИ

d2r'
(r; ˆl, ˆl )
L0 (r, ˆl )
(r; ˆl, ˆl )
r'
( ˆl , ) L(r, ˆl ) 0 :
l'
N'
L(r, l ) r пропускание
x0
N
l
1
L(r, l ) (r; l, l ) ( N, l ) dl
L(r, l ) r излучение L0 (r, l )
dl'
r
1
ˆ , ˆl ) dˆl
L(r, ˆl ) r отражение L(r, ˆl ) (r; ˆl , ˆl ) ( N
(r; ˆl , ˆl ) при
(r; ˆl , ˆl )
(r; ˆl , ˆl ) при
O
1
ˆ , ˆl dˆl
L(r, ˆl ) r пассивной L(r, ˆl ) (r; ˆl, ˆl ) N
r r0 xˆl , L(r, ˆl ) L(r xˆl , ˆl )
L(r, ˆl )
r
1
L0 (r, ˆl )
ˆl, ˆl 0,
ˆl, ˆl 0,
L(r, ˆl ) (r; ˆl, ˆl ) Nˆ , ˆl dˆl
ˆ , ˆl N
ˆ , ˆl
N
1
L(r, ˆl ) L0 (r, ˆl ) L(r , ˆl ) (r; ˆl, ˆl )
d 2 r
2
r r
Bidirectional Scattering Distribution Function – коэффициент
яркости по отражению и пропусканию

7. Интегральные уравнения

ˆ , ˆl ) ( N
ˆ , ˆl )
(N
1
L(r, ˆl ) L0 (r, ˆl ) L(r , ˆl ) (r; ˆl, ˆl ) F (r, r )ds , F (r, r )
(r, r ')
2
( )
(r r )
Искомая функция под знаком интеграла – интегральное уравнение
ˆ , ˆl ) ( N
ˆ , ˆl )
(N
1
K (r , ˆl r, ˆl ) (r; ˆl , ˆl )
(r, r ') – ядро интегрального уравнения
(r r ) 2
Тип
I рода
x
Volterra
Fredholm
f ( x ) K ( x , x ) y ( x )dx
II рода
x
y ( x ) f ( x ) K ( x , x ) y ( x )dx
a
a
b
b
f ( x ) K ( x , x ) y ( x )dx
a
y ( x) f ( x) K ( x , x) y( x )dx
a
Уравнение глобального освещения является интегральным
уравнением Фредгольма II рода – всегда имеет решение!

8. Методы решения интегральных уравнений

b
y ( x ) f ( x ) K ( x , x ) y ( x )dx
a
1. Метод итераций
K ( x , x ) 1:
b
y ( x ) K f ( x ), K f ( x ) K ( x , x )K n 1 f ( x )dx , K 0 f ( x ) f ( x )
n
n
n 1
a
2. Факторизация ядра
b
N
n 1
n 1
a
k 1
K ( x , x ) n ( x ) n ( x ), y ( x ) f ( x ) n ( x ) y ( x ) n ( x )dx , y ( x ) y k k ( x )
N
b
k 1
a
( n , m ) nm : yn f n kn yk , f n f ( x ) n ( x )dx ( f , n ), kn ( k , n )
3. Замена
интеграла квадратурой
b
M
K ( x , x ) y ( x )dx K ( x, x
a
m 1
m
M
) y ( xm ) wm : yn f n K ( xn , xm ) y ( xm ) wm
m 1
Основной путь решения численный методом дискретизации на
основе замены интеграла квадратурой

9. Трассировка лучей (Ray Tracing)

Численное решение интегральных уравнений – замена интеграла суммой → СЛАУ:
M
1
L(ri , ˆl k ) L0 (ri , ˆl k ) L(rj , ˆlij ) (ri ; ˆl, ˆlij ) F (ri , rj )
j 1
Точность решения → мелкая сетка → метод последовательных приближений:
M
1
L (ri , ˆl k ) L( n ) (rj , ˆlij ) (ri ; ˆl, ˆlij ) F (ri , r j ), L(0) (ri , ˆl k ) L0 (ri , ˆl k )
j 1
физически это эквивалентно разложению по кратностям
рассеяния и построению лучей в пространстве:
• обратный ход лучей
• все лучи дают вклад в изображение
• трудно попасть в источник
• только один ракурс
• прямой ход лучей
• формирование 3М изображения
• трудно попасть в камеру
• часть лучей формирует изображение
( n 1)
Главный недостаток трассировки лучей – огромный объем
вычислительной работы

10. Метод излучательности (Radiosity)

Наилучший метод ускорения сходимости переход к конечным пучкам – усреднение по
углу и пространству → медленная угловая зависимость яркости
Наиболее эффективен такой подход при
диффузных поверхностях
M
(r )
L(r)
: M (r) M 0 (r)
M (r ) F (r , r)ds
( )
i K
M i M 0i M j Fij
j 1
• трехмерное изображение
• приемлемое качество за доступное время
• высокая точность расчета освещенности
• отсутствие зеркальных отражений
Впервые метод предложен в работе Z.Yamauti в 1926,
полная теория построена P.Moon в 1940