Фотометрическое приближение (луч света)

1. Фотометрическое приближение (Луч света)

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
: +7 (095) 763-5239
[email protected]

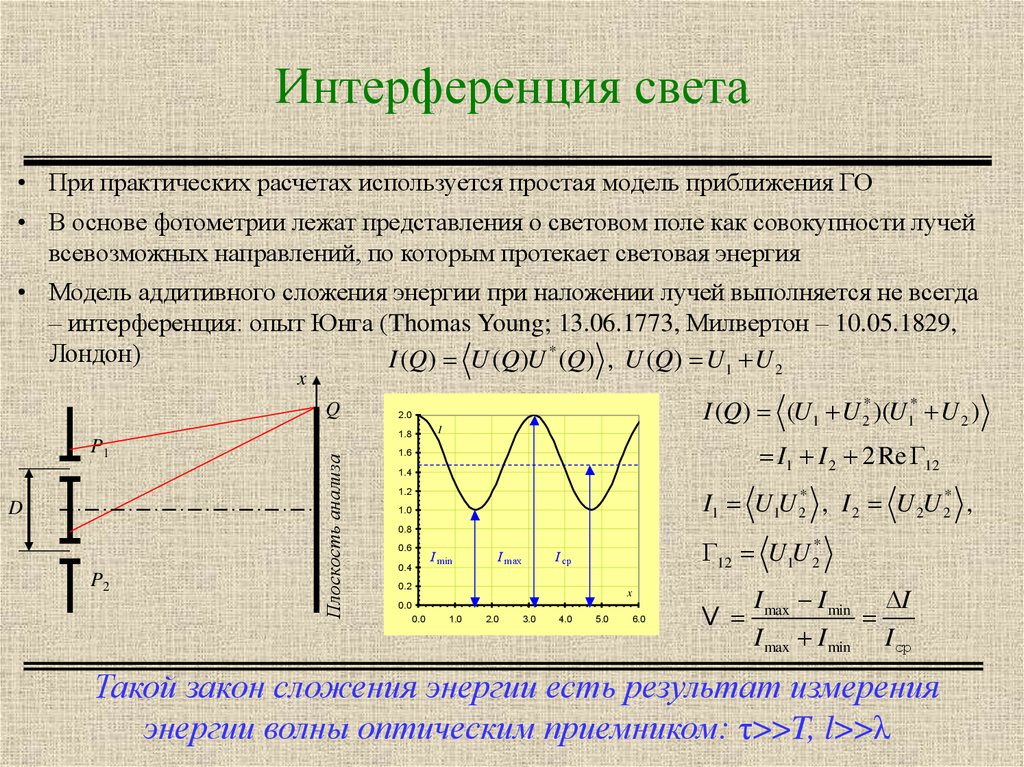
2. Интерференция света

• При практических расчетах используется простая модель приближения ГО
• В основе фотометрии лежат представления о световом поле как совокупности лучей
всевозможных направлений, по которым протекает световая энергия
• Модель аддитивного сложения энергии при наложении лучей выполняется не всегда
– интерференция: опыт Юнга (Thomas Young; 13.06.1773, Милвертон – 10.05.1829,
Лондон)
I (Q) U (Q)U * (Q) , U (Q) U1 U 2
x
Q
D
P2
I
1.8
Плоскость анализа
P1
I (Q) (U1 U 2* )(U1* U 2 )
2.0
I1 I 2 2 Re 12
1.6
1.4
I1 U1U 2* , I 2 U 2U 2* ,
1.2
1.0
0.8
0.6
I min
0.4
I max
12 U1U 2*
I ср
0.2
x
0.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
V
I max I min I
I max I min Iср
Такой закон сложения энергии есть результат измерения
энергии волны оптическим приемником: τ>>T, l>>λ

3. Когерентность света

Корреляционную функцию поля (функция когерентности) можно представить в виде:
12
12
I1I 2
V
12 exp i 12 - степень когерентности
( I1 I 2 2 12
I1I 2 ) ( I1 I 2 2 12
I1I 2 )
( I1 I 2 2 12
I1I 2 ) ( I1 I 2 2 12
I1I 2 )
I (Q) I1 I 2 2 I1I 2 12 cos 12
2 I1I 2
12
I1 I 2
I (Q) 12 I1 I 2 2 I1I 2 cos 12 1 12
I1 I 2 V 12
I
1 I2 :
2.0
Iког
12
I полн
I
1.6
/2
1.2
0.8
0.4
D ( )
0.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
Любое излучение является частично-когерентным: можно
ввести по уровню время τ и пространство когерентности l

4. Распределение энергии в изображении

Корреляционная функция поля в изображении
i ( i , i ) U o ( o )P( o i ) d 2 o U o* ( o )P* ( o i ) d 2 o
o ( o , o )P( o i )P*( o i ) d 2 o d 2 o
или для интенсивности поля
I i ( i ) i ( i , i ) o ( o , o )P( o i )P*( o i ) d 2 o d 2 o
Введем характерные размеры изменения подынтегральный функций: l0 – длина
когерентности излучения и δ – разрешение ОС
1) l0 » δ – когерентность излучения существенно превышает разрешение системы
I i ( i ) o ( o , o )P( o i )P*( o i ) d 2 o d 2 o
U o ( o )U o* ( o ) P( o i )P*( o i )d 2 o d 2 o
U
( o )P( o i )d o U ( o )P ( o i )d o
2
o
*
o
*
2
U
*
o
( o )P ( o i )d o
*
При когерентном освещении ОС линейна
относительно комплексной амплитуды
2
2

5. Некогерентное освещение

2) δ » l0 – разрешение системы существенно превышает когерентность излучения
o ( o , o ) I o ( o ) ( o o )
что приводит к выражению
I i ( i ) o ( o , o )P( o i )P*( o i ) d 2 o d 2 o
I o ( o ) ( o o )P( o i )P*( o i ) d 2 o d 2 o
2
I o ( o )P( o i )P*( o i )d 2 o I o ( o ) P( o i ) d 2 o
ФРТ некогерентного и когерентного освещений связаны
h( o i ) P( o i )
2
При некогерентном освещении ОС линейна
относительно интенсивности излучения

6. ФРТ ОС при когерентном освещении

При круглом входном зрачке радиуса a:
A
A
P ( ) ( w ) exp i 2 w d 2 w
a 2
exp i 2 w cos d wdw
0
0
2 J 0 (2 w )
A
2
a
J 0 (2 w ) wdw 2
0
A 1
a
2 A 2 J1 ( k a )
J
(
2
w
)
2
w
a
1
0
(2 ) 2
2 k a
1.0
i tg
si
0.8
0.6
0.4
0.2
0.0
-10
-8
-6
-4
-2
0
2
4
6
8
-0.2
ФРТ ОС при когерентном освещении
есть кружок рассеяния Airy
10

7. ОПФ ОС при когерентном освещении

H ( ) P( ) ei 2 d 2
1
2 2
i 2
e
(
)
exp
i
2
d d
2
s
i
1
2 2
(
)
exp
i
2
d
d
(
)
si
2
si
a
si
2
d ( si )
a
si
ОПФ ОС при когерентном освещении аналогична
идеальному радиоприемнику

8. ФРТ ОС при некогерентном освещении

2 J1 (ka )
,
ka
2
a 3.83 пр 0.61
a
2
h( ) P( )
2
- предельное разрешение ОС – дифракционное ограничение
1.0
0.8
0.6
0.4
0.2
0.0
-10
-8
-6
-4
-2
0
2
4
6
8
10
-0.2
Сущность построения изображения ОС – дифракция на
выходном зрачке, а ОС - наблюдать на конечном расстоянии

9. ОПФ ОС при когерентном освещении

h( ) P( )
2
H ( ) H ( ) H ( ) si ( w ) si w d 2 w
Свертка геометрически есть объем пересечения двух цилиндров 1 высоты:
a
γ
a
a
Λsiν/2
H ( ) 4( Sсек -S ), Sсек
s a
a 2
1
s
2
a
, S a 0.5 si sin i
1 i
2
2
2
4
2a
2
Расчет объема при 1 высоте можно заменить вычислением
площади пересечения

10. ОПФ ОС

2
a2
si si a
si
H ( ) 4 arccos
1
2
2a
4
2a
1.0
,
0.9
0.8
0.7
0.6
ОПФ
w w
w
H ( w) 2a arccos 1
2 2
2
s
w i , H (0) a 2 ,
2a
2
2
w w
w
T ( w)
arccos 1
2 2
2
2
2
2
si si
si
2
2a arccos
1
2a
2a
2a
0.5
0.4
0.3
0.2
0.1
0.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
w - Относительная пространственная частота
Такую ОПФ можно реализовать в системах ничего не имеющих
общего с оптикой: камера-обскура или непрозрачный шар

11. Распространение функции когерентности

Интенсивность в
произвольной точке :
I (r ) U (r )U * (r) (r, r ) (r1 , r1 ) (r2 , r2 ) 2Re (r1 , r2 )
Функция когерентности двухточечная характеристика:
1 12 k 12 0,
2
2 12 k 12 0,
2
1 2 12 0,
1
2
1 2 12 k 12 0,
2
1
1
1 R , 1 R R ,
2
4
1
1
2 R , 2 R R ;
2
4
1U1 k 2U1 0, U 2*
*
2
2U 2 k U 2 0, U1
1
R (r1 r2 ), r1 r2 ;
2
1
1
r1 R , r2 R ,
2
2
R 12 (R, ) 0,
1
2
k
12 (R, ) 0;
4 R
Распространение функции когерентности описывает не одно
уравнение, а система уравнений

12. Спектр Wigner ( Юджин Вигнер, Wigner Jenő Pál; 17.11.1902, Будапешт – 01.01.1995, Принстон, США)

R 12 (R, ) 0,
1
2
k
12 (R, ) 0;
4 R
Введем Фурье-трансформанту: 12 (R, ) F (R, ei d 3
ς
R0
ˆl
R
R R0 ˆl, ˆl
R F (R, ) 0,
1
2
2
k
R
F (R, ) 0;
4
d
F (R 0 ˆl, ) 0
d
F (R0 , ) F (R0 ˆl, )
функция когерентности вдоль луча не меняется
Луч распространения функции когерентности и луч
приближения ГО в общем случае не совпадают

13. Квазиоднородные волны

1
1
2
k
(
R
,
)
0
R F (k 2 2 ) F 0
R
12
4
4
Определим характерный масштаб LR изменения F по R:
1
L2R
1
k: 2
LR
k k
k 2 2
1
k 2 L2R
или
1
L2R
R F
F
L2R
(k )(k )
k
2
2
, k k : k
2
k
LR
k
k
Допустим, что характерный размер неоднородности волны много больше длины волны:
LR
(k 2 2 ) F
1
R F
4
R 12 (R, ) 12 (R, )
Условие квазиоднородности близко условию применимости приближения ГО
Можно выделить область пространства, где квазиоднородная
волна подобна плоской волне

14. Обобщенная яркость

1
R F (k 2 2 ) F 0 (k 2 2 ) F 0
4
L(R, ˆl )
решение которого имеет вид: F (R, )
( k )
k2
L(R, ˆl )
i 3
i 2
ˆl
ˆl )eik ˆl dˆl
12 (R, ) F (R, )e d
(
k
)
e
k
d
d
(
R
,
)
L
(
R
,
12
k2
0
Для квазиоднородной волны уравнение:
R F (R, ) 0 (ˆl, ) L(R, ˆl) 0 L(R ˆl, ˆl) L(R, ˆl)
По корреляционной функции можно определить дисперсию – плотность мощности и
поток мощности:
I (r ) 12 (R r, 0)
L(r, ˆl )dˆl E0 (r)
S(r )
1
12 (r, 0)
ik
L(r, ˆl )ˆldˆl E(r)
Спектр Wigner не всегда является положительной величиной
как неполное Fourier преобразование – обобщенная яркость

15. Световое поле

12 (R, )
L(R, ˆl)e
ik ˆl
dˆl
2
k
L(R , ˆl ) l 12 (R , )exp( ikˆl )d 2
2
1. Электромагнитное поле представляется совокупностью лучей –
приближение геометрической оптики
2. Лучи приходящие с различных направлений некогерентны между собой
3. Постоянная времени и характерный размер квадратичного оптического
приемника существенно превышают период и длину волны – применимость для исследований выводов статистической теории
4. Поле эргодично: усреднение по реализации соответствует усреднениям по
ансамблю реализаций – соответствие теории с практическими измерениями
(ˆl , ) L(R, ˆl ) 0 L(R ˆl, ˆl ) L(R, ˆl )
Отрицательные значения обобщенной яркости несут
информацию о фазе волны и корреляции точек

16. Дифракция на диафрагмах в ОС

• Формирование изображения в ОС описывается приближением дифракции
Фраунгофера
• Волновое поле в этом приближении является квазиоднородным
• Описывается в лучевом приближении
Выходной
зрачок
U
U
Принцип Abbe (Abbe Ernst, 1840–1905): структуру оптического изображения можно исследовать в приближении ГО с
привлечением дифракции на выходном зрачке
U (r ) (r )U (r )
(r1, r2 ) o (r1, r2 ) (r1 ) (r2 )
*
(r1 , r2 ) U (r1 )U (r2 )
r r
R 1 2 , r1 r2 (R, ) o (R, ) R R
2
2
2
o ( R , )
L(R, ˆl )e
2
ikˆl
k
dˆl , L(R, l ) lz (R, )eikl d 2
2
В системах формирования изображения дифракция на
выходном зрачке описывается в лучевом приближении

17. Дифракция на диафрагмах в ОС

Выходной
зрачок
ˆ
k
L(R, l ) lz Lo (R, ˆl )e ikl dˆl R R eikl d 2
2
2
2
2
k
L(R, l ) lz Lo (R, ˆl ) R R exp ik (l l ) d 2 dˆl
2
2
2
2
h ( l l )
L(R, l ) Lo (R, l )h(l l )d 2l
k lz
h(l l ) (R ) (R )exp ik (l l ) d 2
2 lz
2
- ФРТ диафрагмы в угловых переменных
Дифракция в лучевом приближении эквивалентна рассеянию
излучения на молочном стекле

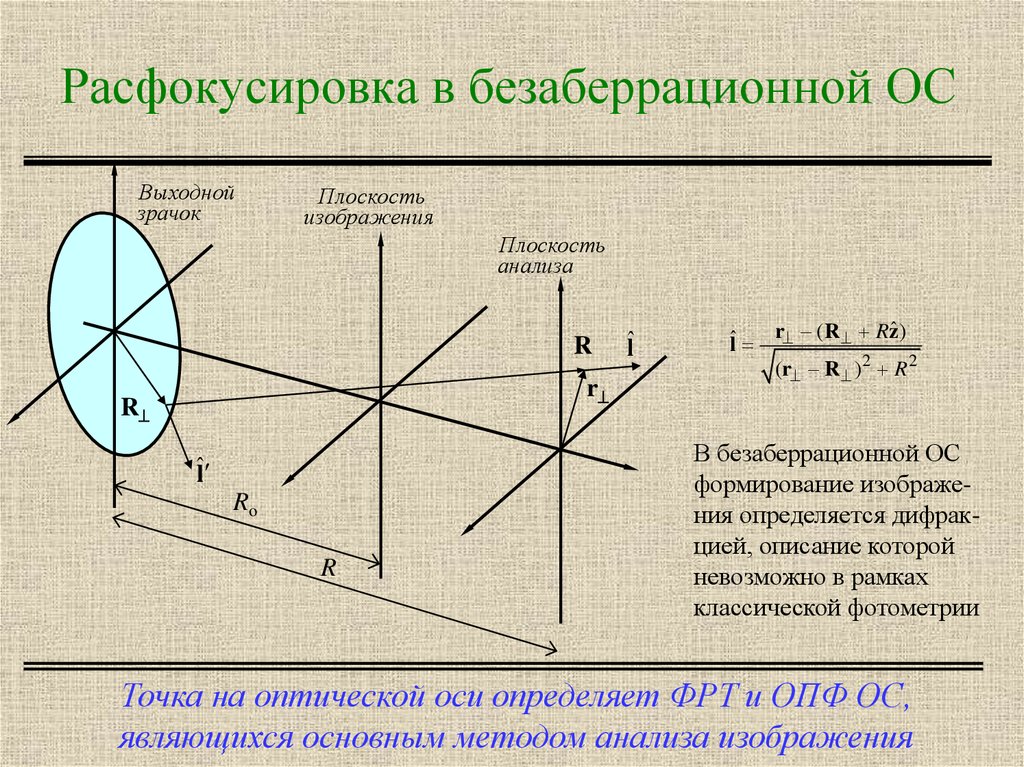
18. Расфокусировка в безаберрационной ОС

Выходной
зрачок
Плоскость
изображения
Плоскость
анализа
R
r
R
ˆl
Ro
R
ˆl
ˆl r (R Rzˆ )
(r R )2 R 2
В безаберрационной ОС
формирование изображения определяется дифракцией, описание которой
невозможно в рамках
классической фотометрии
Точка на оптической оси определяет ФРТ и ОПФ ОС,
являющихся основным методом анализа изображения

19. Облученность в изображении

Выходной
зрачок
ˆl
R
Lo (R , l ) I o l
Ro
R
Ro
k
L (R , l ) I o
2
2
l
R
z R R exp ik l d 2
l z
2
2
Ro
1
E (r )
( )
ˆl r (R Rzˆ )
(r R )2 R 2
I k
E (r ) o2
R 2
l
2
r R
,
R
La (r , l )l z dˆl
La (r , l )l z d 2l
( )
R Ro
R r
R
d 2R
2
l
,
, d l 2
Ro
R
R
Ro
R
r
R 2 2
R
R
exp
ik
d d R
2 2 R
R
ОПФ ОС является Фурье преобразованием от распределения
облученности в плоскости анализа

20. ОПФ ОС

H ( ) E (r ) e
i r
I k
d r o2
R 2
2
I k
H ( ) o2
R 2
2
2
r
R
2
2
2
i r d r d d R
R
R
k
d 2 r d 2 d 2 R
exp ir
R
R
R
R k
2 2
R
R
e
xp
ik
d
d
R
,
2 2 R R
k
2 R Io k
H ( )
k R2 2
2
2
R
R
2 2 exp i R d R
2
H ( ) I o R
R
exp i R d R
2
2
T ( )
R 2 R 2 exp ik R
R 2 R 2 exp ik
I k
H ( ) 2 o2
R 2
2
2
H (0) Io (R )d 2 R a2 Io
H ( )
1
2
2 R
R
exp i R d R
H (0) a
2
2
При β→0 выражение переходит в ОПФ для ОС, ограниченной
дифракцией

21. Преобразования интегрального выражения

2
Y
2
2
x
y a :
2
x1
a 2 y 2 , x2
a2 y2 ,
2
2
a
X
a
T ( )
T ( )
2
a 2
a2
2
0
a2
2
2
a
2
2
4
sin a 2 y 2
dy T ( w)
2
w
2
a2 y2
2
2 2
y12 a
4
2
ei x dx dy
a2 y2
2
0
w2
1
4
0
w
sin w 1 t 2 dt
2
R R
y
a 2 ka 2
a
2 a
w
, t ,
, ka
a
ak
a
R
R
Полученный интеграл при произвольной расфокусировке через
элементарные функции не выражается

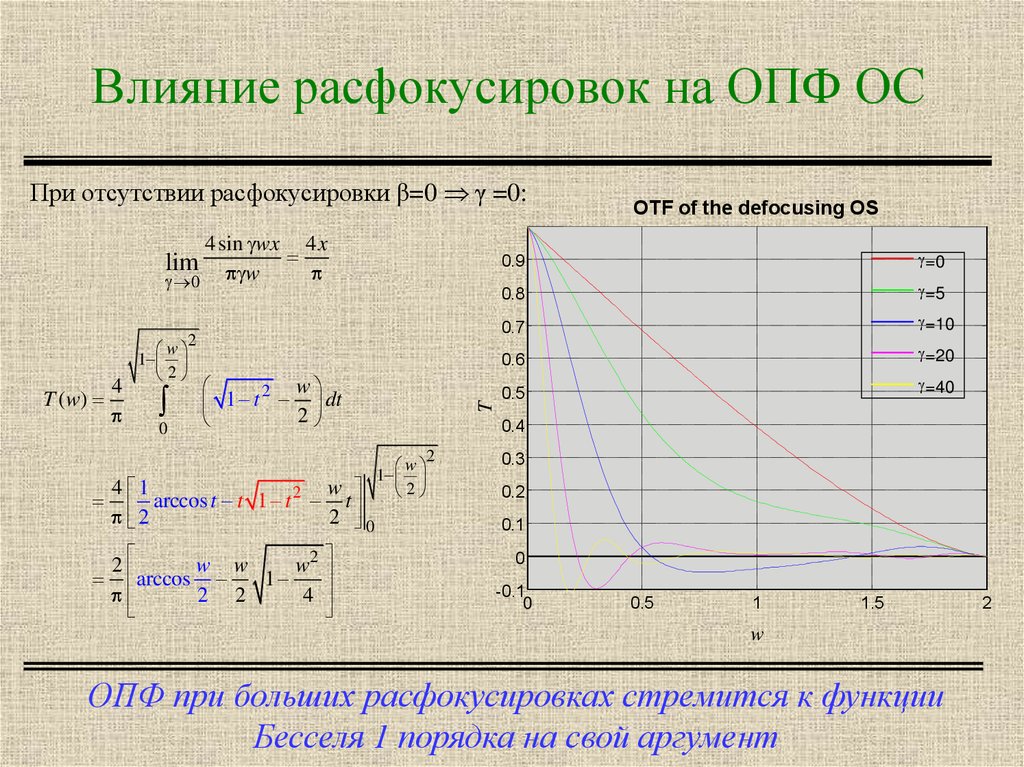
22. Влияние расфокусировок на ОПФ ОС

При отсутствии расфокусировки β=0 γ =0:
4 sin wx 4 x
w
0
lim
4
0
w
2
1 t dt
2
4 1
w
2
arccos
t
t
1
t
t
2
2 0
2
w w
w2
arccos
1
2 2
4
T
T ( w)
2
w
1
2
OTF of the defocusing OS
0.9
=0
0.8
=5
0.7
=10
0.6
=20
0.5
=40
0.4
w
1
2
2
0.3
0.2
0.1
0
-0.1
0
0.5
1
1.5
w
ОПФ при больших расфокусировках стремится к функции
Бесселя 1 порядка на свой аргумент
2