Фотометрическое приближение

1. Фотометрическое приближение

Будак Владимир Павлович,
Московский энергетический институт (ТУ)
кафедра светотехники
: +7 (495) 763-5239
[email protected]

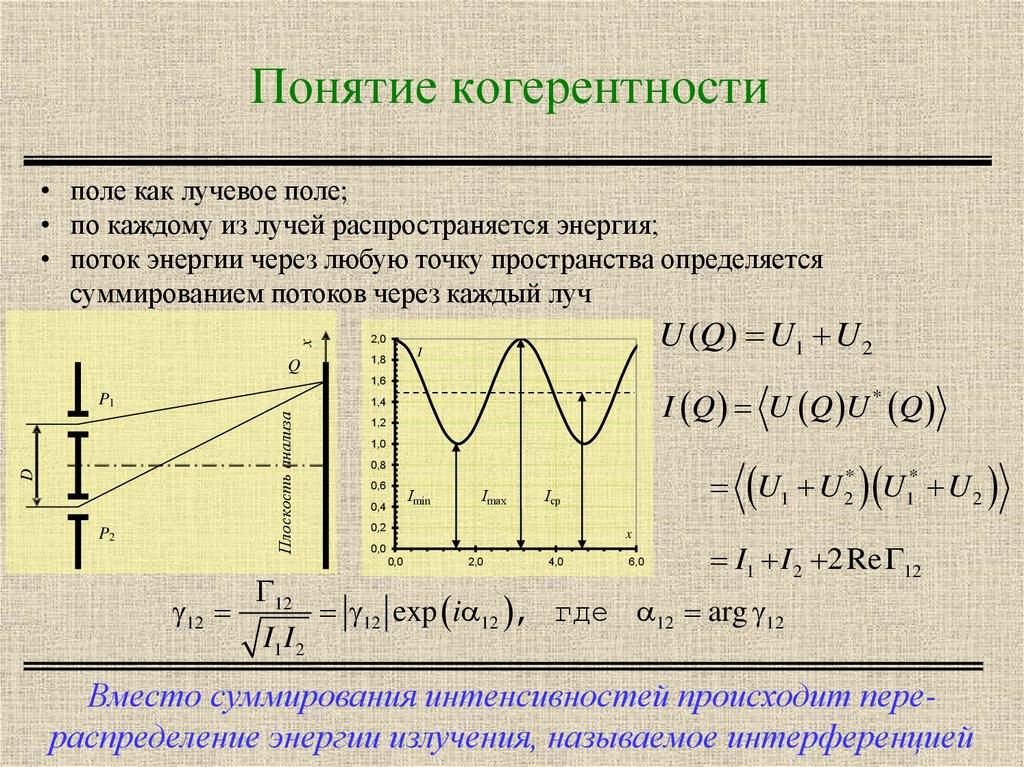
2. Понятие когерентности

x
• поле как лучевое поле;
• по каждому из лучей распространяется энергия;
• поток энергии через любую точку пространства определяется
суммированием потоков через каждый луч
Q
P2
I
1,8
1,6
I Q U Q U * Q
1,4
Плоскость анализа
D
P1
U (Q) U1 U 2
2,0
1,2
1,0
U1 U 2* U1* U 2
0,8
0,6
Imin
0,4
Imax
Iср
0,2
x
0,0
0,0
2,0
4,0
6,0
I1 I 2 2 Re 12
12
12
12 exp i 12 , где 12 arg 12
I1 I 2
Вместо суммирования интенсивностей происходит перераспределение энергии излучения, называемое интерференцией

3. Видность интерференционных полос

I (Q) I1 I 2 2 I1 I 2 12 cos 12
I max I min I
V
I max I min I ср
V
( I1 I 2 2 12
I1 I 2 ) ( I1 I 2 2 12
I1 I 2 )
( I1 I 2 2 12
I1 I 2 ) ( I1 I 2 2 12
I1 I 2 )
2 I1 I 2
I1 I 2
12
Последнее выражение особенно наглядно, если в опыте сделать
совершенно одинаковые отверстия:
I1 I 2 V 12
Степень когерентности определяет видимость интерференционной картины: 12=0, то интенсивности складываются

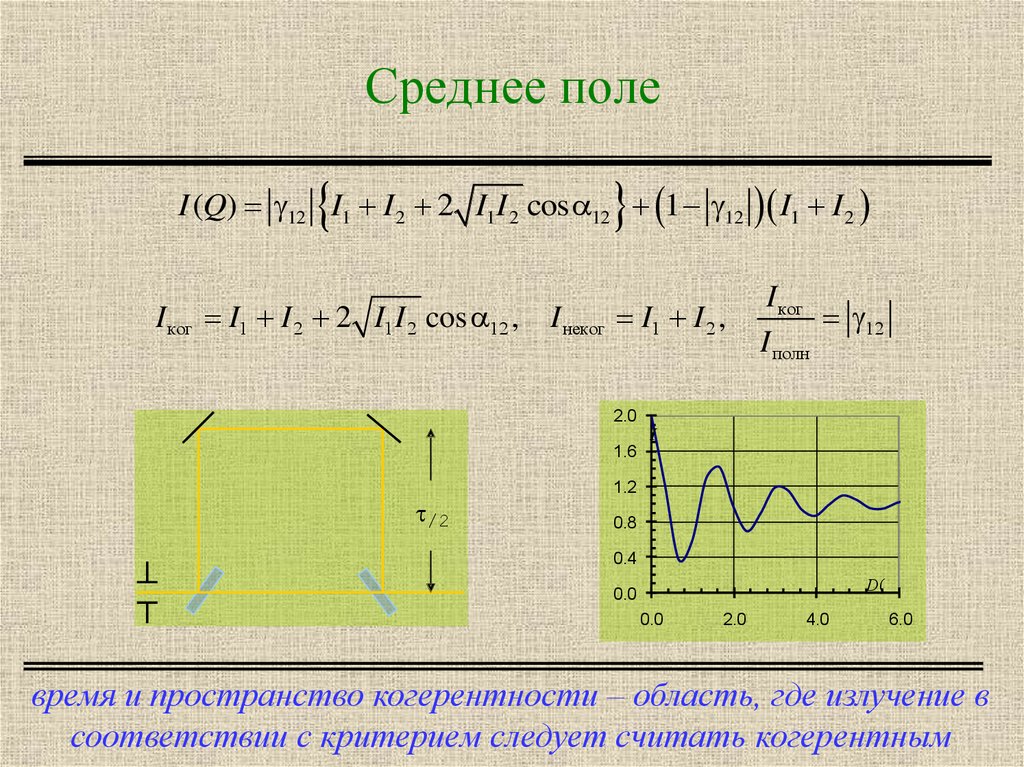
4. Среднее поле

I (Q) 12 I1 I 2 2 I1I 2 cos 12 1 12
I ког I1 I 2 2 I1 I 2 cos 12 , I неког I1 I 2 ,
2.0
1.6
/2
I
1
I2
I ког
12
I полн
I
1.2
0.8
0.4
D(
0.0
0.0
2.0
4.0
6.0
время и пространство когерентности – область, где излучение в
соответствии с критерием следует считать когерентным

5. Распространение функции когерентности

I (r ) I (r1 ) I (r2 ) 2 Re (r1 , r2 )
I (r) U (r)U * (r) (r, r) I (r) (r1 , r1 ) (r2 , r2 ) 2Re (r1 , r2 )
1U1 k 2U1 0,
2
2U 2 k U 2 0,
1 12 k 2 12 0,
2
2 12 k 12 0,
1
R (r1 r2 ), r1 r2
2
1
1
r1 R , r2 R
2
2
1 2 12 0,
1
2
k
12 0
1
2
12
2
r1
R
ρ
r2
координата центра тяжести и разностной координатой

6. Уравнение распространения когерентности

1
1
1 R , 1 R R ,
2
4
1
1
2 R , 2 R R
2
4
R 12 (R , ) 0,
1
2
k
12 (R , ) 0
4 R
R F ( R , ) 0,
12 ( R , ) F ( R , ei d 3 1
2
2
k
F ( R , ) 0.
4 R
R R 0 ˆl
d
F (R 0 ˆl , ) 0
d
F (R 0 , ) F (R 0 ˆl , )
Луч распространения функции когерентности и луч приближения геометрической оптики в общем случае не совпадают

7. Квазиоднородные волны

1
R F (k 2 2 ) F 0, R F
4
1
L2R
k
2
2
1
L2R
или
2
L2R
(k )(k )
k
k
1
L2R
F
L2R
k k
1
k 2 L2R
k
k
1
(k 2 2 ) F R F
4
R 12 (R, ) 12 (R, )
Можно выделить область пространства, где квазиоднородная
волна ведет себя приблизительно подобно плоской волне

8. Световое поле

L(R, ˆl )
F (R, )
( k )
2
k
(k ) F 0
2
2
L(R, ˆl )
i 2
ˆl
12 (R, ) F (R, )e d
(
k
)
e
k
d
d
2
k
0
i
12 (R, )
3
ˆl )eik ˆl dˆl (ˆl , ) L(R, ˆl ) 0 : L(R ˆl , ˆl ) L(R, ˆl )
L
(
R
,
I (r) 12 (R r, 0)
L(r, ˆl)dˆl,
S(r)
1
12 (r, 0)
ik
L(r, ˆl)ˆldˆl
2
k
L(R , ˆl ) l 12 (R , )exp( ikˆl )d 2
2
Отрицательные значения обобщенной яркости несут
информацию о фазе волны и корреляции точек

9. Аксиомы светового поля

1. Электромагнитное поле представляется совокупностью
лучей – приближение геометрической оптики.
2. Лучи приходящие с различных направлений некогерентны
между собой.
3. Постоянная времени и характерный размер квадратичного
оптического приемника существенно превышают период и
длину волны – применимость для исследований выводов
статистической теории.
4. Поле эргодично: усреднение по времени соответствует
усреднениям по ансамблю реализаций – соответствие теории
с практическими измерениями.