Архитектура краевых задач теории переноса изображения через слой мутной среды

1. Архитектура краевых задач теории переноса изображения через слой мутной среды

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
Tomoyuki Nishita (Fukuyama University), Eihachiro
Nakamae (Hiroshima Prefectural University)
: +7 (095) 763-5239
[email protected]

2. Краевая задача теории переноса изображения

d
( nˆ , nˆ S )
(nˆ , nˆ R )
0
1
2
(
r
)
d
r , (r ) ( r )
S (S )
z
(nˆ , nˆ
S
)(nˆ , nˆ S )dnˆ d 2 r 1,
(S)
(r )
(nˆ , nˆ
R
)(nˆ , nˆ R )dnˆ d 2 r 1
( R)
P (nˆ S , nˆ R )
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
(
n
,
n
)
L
(0,
r
,
n
)
(
n
,
n
)
d
n
d
r
R
R
R
( R)
( z )
Краевая задача: (ˆl , ) L( z, r, ˆl ) ( z ) L( z, r, ˆl )
4
L1 L(0, r, ˆl ) ˆ
l
L2 L( z0 , r, ˆl ) ˆ
x( z, ˆl, ˆl ) L( z, r, ˆl )dˆl
0 (r, ˆl ),
l
( z )
L( z0 , r, ˆl )(ˆl, zˆ )dˆl RL
( )
Имеем по сути систему интегральных уравнений

3. Яркость атмосферной дымки

Вследствие линейности уравнения переноса представим решение в виде суммы:
L( z, r, ˆl ) D( z, r, ˆl ) LS ( z, r, ˆl )
каждое слагаемое которой удовлетворяет краевым зачам
D(0, r, ˆl ) 0 (r, ˆl );
ˆ
D( z0 , r, l ) 0;
Допустим известна функция Green УПИ:
LS (0, r, ˆl ) 0;
ˆ
LS ( z0 , r, l ) R( LS D);
l ( z; r , ˆl r, ˆl )
D( z , r, ˆl ) 0 l ( z; r , ˆl r, ˆl ) (r , ˆl ) dˆl d 2 r 0l (r , ˆl )
Поскольку (r , ˆl ) (r r ) (ˆl ˆl ) (r , ˆl )dˆl d 2 r (r , ˆl ) , то
l 1 (r r ) (ˆl ˆl );
l 2 0;
Яркость дымки – компонента яркости в среде, обусловленная
только обратным рассеянием

4. Отражение от подстилающей поверхности

Вторую краевую задачу проанализируем на основе теории возмущений, считая
отражение от объекта малым параметров:
(r)d
2
r S : , LS
n L(n)
n 0
Подставим ряд во второе граничное условие, что приведет к выражению
n 0
n L(2n )
n (n)
( )R L D
n 0
Откуда, приравнивая члены при одинаковых степенях ξ - если равны ряды, то равны
коэффициенты ряда:
(0)
(0)
n 0:
L2 RL
RD;
n 1:
(1)
(0)
L(1)
D );
2 RL R ( L
n 2:
L(2n ) RL( n ) RL( n 1) ;
Независимо от номера n все уравнения имеют одинаковую структуру:
L 2 RL G
Система уравнений представляет последовательность
уравнений для яркости n-той кратности отражения

5. Оптический передаточный оператор

Возьмем Фурье-преобразование от обоих частей уравнения
1
( z , , ˆl )
L ( z, r, ˆl ) e i r d 2 r F L , G ( F G 2 R G ( )
2
1 0; - преобразование Fourier от яркости ТД:
ˆ
ˆ
(
z
,
,
l
)
R
G
(
)
(
z
,
,
l
)
Пусть
e( z; r r ) F 1
2 1.
Соответственно
( z , , ˆl ) R G ( ) ( z , , ˆl ) R R G ( ) R , R C (
- среднее полусферическое альбедо слоя мутной среды
R
G ( ) C ( )
G ( ) C ( )
G ( )
( z, , ˆl )
G ( ) ( z, , ˆl )
( z, , ˆl )
1 C ( )
1 C ( )
1 C ( )
L ( z, , ˆl )
1
G ( )
( z, , ˆl )ei r d 2
2 1 C ( )
С
ρ
ρ
Решение имеет структуру аналогичную фотометрическому
шару

6. Компоненты сигнала

1. Яркость дымки D( z, r, ˆl) 0 l (r , ˆl ) - связана только со свечением среды под влиянием
многократного рассеяния в среде – помеха обратного рассеяния.
2. Яркость (сигнал) подложки
L ( z, r, ˆl ) L(0) ( z, r, ˆl )
G ( ) F RD F R 0l 0 F Rl (r , ˆl )
0
ˆl 0 F e F dˆl
G
(
)
F
d
1
1
e
*
Rl l ( z; r , ˆl r, ˆl )(zˆ , ˆl ) dˆl e( z; r r )
( )
0
E ( )
ˆl ) ei r d 2 , E ( ) 1 F e F dˆl
L ( z , r, ˆl )
(
z
,
,
2 C (
3. Яркость сигнала – линейная часть от составляющей : L( z, r, ˆl ) L(1) ( z, r, ˆl )
G ( ) F R ( L D) ( ) F RL F RD d 2 1
E ( )
E ( )
E ( )
F RD 0 E ( ), F RL 0
R ( z, ˆl ) 0
C ( ) F RD F RL 0
1 C ( )
1 C ( )
1 C ( )
E ( 1 )
L( z , r, ˆl ) 0 ( 1 )
d 2 1 ( z, , ˆl ) ei r d 2
2
C ( 1
Все компоненты сигнала выражаются через яркость
ТМ и ТД источника

7. Нелинейная часть сигнала

4. Яркость света, многократно отраженного от объекта L ( z, r, ˆl )
G ( ) F RL
( n 1)
( n 1)
L
( 1 ) E
E ( n 1) 1 )
ˆ
( z , l ) ( 1 )
( z, , ˆl ) d 2 1
C ( 1 )
причем
(n)
( 1 )d 1
E ( ) F RL
E (1) ( ) F RL(1) 0 ( 1 )
Следовательно
E ( n ) ( ) C ( )
C 1 )
C 2 )
C ( 1 ) C ( 2 )
C 1 )
C 2 )
L( n ) ( z , r, ˆl ) 0
2 C ( 1 ) C ( 2 )
( n 1)
E ( n 1) 1 )
C ( )d 2 1
( 1 )
C ( 1 )
E 1 )
C ( )d 2 1
C ( 1 )
E n )
( 1 )
C ( n )
E n )
( 1 )
C ( n )
L(n) ( z, r, ˆl )
n 2
2
(n)
( n 1 n ) d 2 1
d 2 n
( n 1 n ) ( z, , ˆl )ei r d 2 1
d 2 n d 2
Многократные отражения от объекта делают слой мутной
среды нелинейной системой

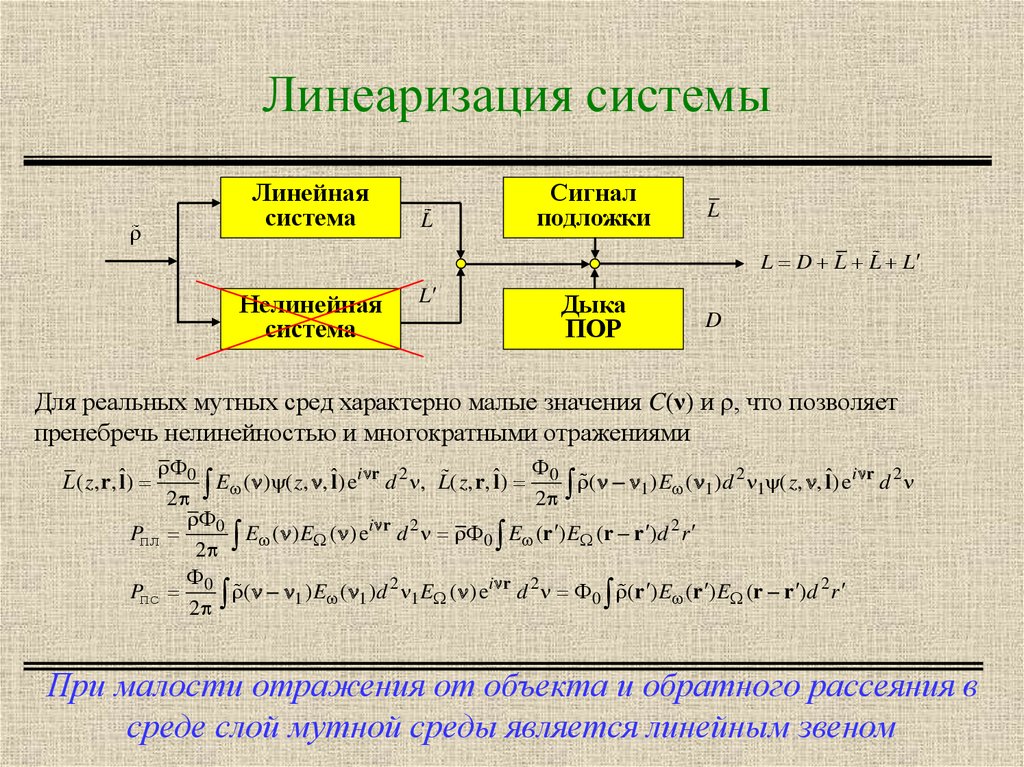
8. Линеаризация системы

Линейная
система
L
Сигнал
подложки
L
L D L L L
Нелинейная
система
L
Дыка
ПОР
D
Для реальных мутных сред характерно малые значения C(ν) и ρ, что позволяет
пренебречь нелинейностью и многократными отражениями
0
ˆl ) ei r d 2 , L( z, r, ˆl ) 0 ( ) E ( )d 2 ( z, , ˆl) ei r d 2
L ( z, r, ˆl )
E
(
)
(
z
,
,
1 1
1
2
2
0
Pпл
E ( ) E ( ) ei r d 2 0 E (r ) E (r r )d 2 r
2
Pпс 0 ( 1 ) E ( 1 )d 2 1 E ( ) ei r d 2 0 (r ) E (r ) E (r r )d 2 r
2
При малости отражения от объекта и обратного рассеяния в
среде слой мутной среды является линейным звеном