Ряды. Числовые ряды. Общие определения и свойства. Сходимость рядов. Признаки сходимости. Функциональные ряды. (Лекция 13)

1. Лекция 13

Ряды. Числовые ряды. Общие
определения и свойства. Сходимость
рядов. Признаки сходимости.
Функциональные ряды.

2.

Пусть дана бесконечная последовательность чисел u1 , u2 ,..., un
Определение
Выражение u1 u2 ,..., un ... называется рядом, а числа u1 , u2 ,..., un
- элементы (члены) ряда.
Короткая форма записи u n , u n - общий элемент ряда.
n 1
Ряд считается заданным, если известно правило, по которому для
любого номера n можно записать соответствующий элемент ряда: u n f (n)
Если формула u n f (n) дана, то можно сразу записать любой
элемент ряда.
Примеры:
1
1 1
1
u n n ... n ...
2
2 4
2
1
1 1
1
u n 1 ... ...
n!
2! 3!
n!
Иногда ряд задается при помощи рекурентного соотношения,
которое связывает последующий член с предыдущими.
Например:

3.

Например: u1 1, u 2 1 , u n 1 u n 1 1 u n 2
2
2
3
Последовательно находим : u 1 1 1 1 7
3
2 2 3
12
и так далее.
Получаем ряд : 1 1 7 11 ...
2
12
u4
1 7 1 1 11
2 12 3 2 24
24
Пусть дан ряд: u u ,..., u .. ; S u u ,..., u частичная
1
2
n
n
1
2
n
сумма ряда.
Образуем последовательность частичных сумм ряда:
S1 u1 ; S 2 u1 u2 ;...S n u1 u2 ... un ;....
С неограниченным увеличением числа n в сумме S n учитывается все
большее и большее число элементов ряда.
Определение
Если при n существует предел последовательности частичных сумм
данного ряда lim n Sn S , ряд называется сходящимся, число S – его
суммой.
Запись: S u1 u2 ,..., un ...

4.

Если последовательность частичных сумм не стремится к пределу, то ряд
называется расходящимся.
Замечание
Ряд может расходиться в двух случаях:
• Если последовательность S n
• Если последовательность S n вообще не имеет предела (ни конечного, ни
бесконечного)
Пример
Рассмотрим сумму элементов бесконечной геометрической
прогрессии
n
a aq aq 2 ... aq n ...(a 0) S n a
1 q
1 q
1 qn
a
lim
q
0
lim
S
a
lim
Если |q|<1, то
.
n
n
n
n
1 q 1 q
Следовательно, при |q|<1 бесконечная геометрическая прогрессия образует
сходящийся ряд, сумма которого равна S a
n
1 q
n
1
q
n
, то есть ряд
Если же |q|>1, то lim n q lim n Sn a lim n
1 q
расходится.

5.

Пусть q=1. Ряд a a ... a ...(a 0) имеет S n na . Ряд расходится.
a , то есть S не
Пусть q=-1. Ряд a a ... a ...(a 0) имеет S
n
n
стремится ни к какому пределу.
0
Согласно определению это ряд расходится.
Таким образом, бесконечная геометрическая прогрессия представляет ряд,
который сходится при |q|<1 и расходится, при
.
| q | 1
В рассмотренном примере сходимость и расходимость устанавливалась
непосредственным определением сходимости и известной формулой для
частичной суммы.
Однако в большинстве случаев это способ не применим, так как очень
трудно найти компактную форму для S n , а значит и предел S n .
Выяснять сходимость ряда можно с помощью признаков сходимости.
Рассмотрим сходящийся ряд: S u1 u2 ,..., un ..
Определение
Разность между суммой ряда и его n-ой частичной суммой называется n-ым
остатком ряда. Остаток ряда в свою очередь есть сумма бесконечного ряда.
Обозначение rn S S n u n 1 u n 2 ...

6.

Исходный ряд по определению сходится, то есть lim n S n S следовательно,
| rn | | S S n | будет как угодно мало, если n взять достаточно большим.
Таким образом можно приближенно подсчитать сумму сходящегося ряда,
взяв достаточно большое число первых его элементов. Однако большую
трудность представляет выяснение величины возникающей ошибки.
Свойства сходящихся рядов.
1. Если ряд u1 u 2 ... u n ... сходится и имеет сумму S, то ряд
образованный из произведений всех элементов данного ряда на одно и то же
число k: ku1 ku2 ... kun ... также сходится и имеет сумму kS.
Доказательство
S n - частичная сумма первого ряда;
n - частичная сумма второго ряда.
n ku1 ku2 ... kun kSn lim n n k lim n S n kS
2. Если сходятся ряды
S ' u1 u 2 ... u n ...
S" v1 v2 ... vn ...

7.

То ряд образованный сложением соответствующих элементов данных рядов
то же сходится и его сумма равна S’+S”
Доказательство
S n' - частичная сумма первого ряда;
S n" - частичная сумма второго ряда;
n - частичная сумма полученного ряда;
Тогда
n (u1 v1 ) (u 2 v2 ) ... (u n vn ) S n' S n'' lim n n lim n (S n' S n'' ) S ' S ' '
Замечание
(u1 v1 ) (u 2 v2 ) ... (u n vn )... S ' S '
3. Если ряд сходится, то сходится и ряд, полученный из данного путем
приписывания или отбрасывания любого конечного числа элементов.
Доказательство
Пусть ряд u1 u 2 ... u n ... сходящийся.
Выбросим из него конечное число элементов, например u 2 , u5 , u10 , u15 ,(не
меняя нумерации считаем, что на их места поставлены 0).

8.

Тогда при n>15 частичные суммы будут отличаться друг от друга на
постоянное слагаемое . Если существует предел одной частичной суммы, то
существует и предел второй, причем они отличаются друг от друга на
постоянное слагаемое.
Совершенно аналогичные рассуждения в случае приписывания к ряду новых
элементов.
Следствие Если сходится ряд, то сходится и любой его остаток, и наоборот.
Необходимый признак сходимости ряда. Гармонический ряд.
Если ряд сходится, то общий элемент стремится к нулю при
возрастании его номера.
Доказательство
Имеем S n u1 u2 ... un S n 1 un .
Если ряд сходится, то lim n S n 1 S и lim n S n S . Поскольку
lim n un lim n (S n S n 1 ) lim n S n lim n S n 1 0
Из доказанного вытекает достаточный признак расходимости ряда.
Если u n не стремится к нулю, то ряд не может быть сходящимся.

9.

Пример
1
2
n
...
... ряд расходится, так как
101 201
100n 1
lim n
n
1
0
100n 1 100
Следует помнить, что стремление n-го элемента к нулю не является
достаточным для сходимости ряда.
Рассмотрим ряд 1 1 1 ... 1 ... - гармонический ряд.
2 3
n
lim n u n 0 , но ряд расходится. Покажем, что lim n S n .
Для доказательства заменим некоторые элементы ряда меньшими числами и
убедимся, что даже сумма меньших слагаемых будет стремиться к
бесконечности.
Сделаем разбиение ряда на группы:
1 1 1
1 1 1 1
1
1
1
1 ( ) ( ) ( ... ) ... ...
2 3 4
5 6 7 8
9
16
n
Следующая замена
1 1 1 1 1 1 1
1
1
1
1 ( ) ( ) ( ... ) ... ...
2 4 4 8 8 8 8 16 16
n
1
сумма каждой скобки равна .
2

10.

Поскольку таких скобок можно брать сколько угодно, то сумма стремится
к бесконечности.
Таким образом, частичные суммы ряда неограниченно возрастают,
следовательно, ряд расходится.
Пример
1
1
1
1
...
... ряд расходится, так как даже при выполнении
2
3
n
необходимого признака u n 0 при
n Sn 1
1
2
1
3
...
1
n
1
n
1
n
1
1
n
...
n
n
n
n
Ряды с положительными элементами. Достаточные признаки
сходимости.
1. Признаки сравнения
Рассмотрим ряд u1 u 2 ... u n ...(u n 0)
Лемма Если частичные суммы ряда с положительными элементами
ограничены сверху, то ряд сходится. ( S n M )
Доказательство

11.

Доказательство
Так как un 0 , то частичные суммы ряда по мере возрастания числа
элементов тоже возрастают S1 S 2 ... S n ...
Но если последовательность монотонно возрастает и ограничена сверху, то
по признаку Вейерштрасса она имеет предел, также не превосходящий числа
М. Следовательно, имеем lim n S n S M . Верно обратное. Если ряд с
положительными элементами сходится, то его частичные суммы меньше
суммы ряда: S n S .
Замечание
Если ряд с положительными элементами расходится, то его частичные
суммы
стремятся к бесконечности, то есть lim n S n или другая запись
u n
.
n 1
Признак сравнения
Пусть
даны два ряда с положительными элементами: u k ; (u k 0) (1) и
k 1
v
;
(
v
0
)
(2) и пусть каждый элемент ряда (1) не больше
k
k
k 1
соответствующего элемента ряда (2) u k v k (*).

12.

Тогда
1) Если сходится ряд (2), то сходится и ряд (1)
2) Если расходится ряд (1), то расходится и ряд (2)
Доказательство
n
n
Докажем первую часть теоремы. Полагаем S n u k ; (u k 0) , n vk ; (vk 0)
k 1
k 1
По условию ряд (2) сходится, поэтому n , где - сумма ряда (2). А из
условия (*) следует, что S n n . Получаем, что частичные суммы ряда (1)
ограничены сверху. В силу доказанной выше леммы ряд (1) сходится.
Для доказательства второй части достаточно заметить, что, поскольку ряд
(1) расходится, то его суммы неограниченно возрастают:S n .
Так как S n , то и n . Следовательно ряд (2) расходится.
Признаки сравнения применимы и в том случае, когда условию (*)
удовлетворяют элементы ряда не при всех n, а лишь начиная с некоторого
n=N. Это следует из третьего свойства сходящихся рядов.
Примеры:

13.

Примеры:
1
1
1
1 1
1
1. Ряд 1 ... ... расходится, так как гармонический ряд 1 ... ...
2
3
1
n
2 3
n
1
n
расходится, а n
при n>1
2. Ряд 1 1 2 1 3 ... 1 n ... сходится, так как сходится ряд 1 12 13 ... 1n ...
2 2 2 3 2
2 2
n 2
2
2
1
1
(убывающая геометрическая прогрессия) и n 2 n 2 n
Замечание
На практике признаки сравнения наиболее удобно применять в следующем
виде:
un
Если lim n A 0 , то ряды (1) и (2) или оба сходятся, или оба расходятся.
vn
Доказательство
Из определения предела следует, что для всякого 0 можно указать такое
число N, что при всех n>N будет справедливо неравенство u n A A u n A
vn
vn
где 0 настолько мало, что A 0 .

14.

Предположим сначала, что ряд (2) сходится. Тогда по свойству (1) сходится и
ряд с общим элементом ( A )v n и по признаку сравнения сходится ряд (1)
так как u n vn ( A ) .
Наоборот, если ряд (2) расходится, то из неравенства u n vn ( A ) будет
следовать, что расходится ряд (1).
Пример:
2n
1
Ряд 2 расходится, так как, выбирая v n - гармонический ряд и
un 2
n
n 1 3n 1
lim
0
вычисляем
n
vn 3
В качестве эталонов для сравнения рядов выбирают: гармонический ряд –
расходящийся; бесконечно убывающая геометрическая прогрессия или ряд
обратных квадратов – сходящиеся.
2. Признак Даламбера
Рассмотрим ряд u1 u 2 ... u n ...(u n 0) (*)
Если при n существует предел отношения последующего элемента к
u n 1
, то при 1- ряд сходится; 1 - ряд
предыдущему, то есть lim n
un
расходится; 1 - признак Даламбера не действует.

15.

Доказательство
Пусть 1 . В силу определения предела всегда можно выбрать такое
число N. Что при всех n N будет справедливо неравенство u n 1 1
un
, где 0 берется настолько малым, что 1 1
Тогда u N 1 1 , u N 2 1 , u N 3 1 ,...
uN
u N 1
u N 2
получаем неравенства:
u N 1 1u N ,
u N 2 1u N 1 12 u N ,
u N 2 1u N 2 13u N
...
Отсюда вытекает, что элементы ряда u N 1 u N 2 u N 3 ... представляющего
N-ый остаток данного ряда, меньше соответствующих элементов бесконечно
убывающей геометрической прогрессии 1u N 12u N 13u N ....( 1 1)
Следовательно N-ый остаток ряда сходится, тогда сходится и сам ряд.
Пусть 1.В силу определения предела всегда можно выбрать такое число N.
u
Что при всех n N будет справедливо неравенство n 1 1 u n 1 u n
un

16.

Но тогда каждый последующий элемент ряда будет больше предшествующего
и, поскольку все они положительны, не может выполняться необходимый
признак сходимости ряда, согласно которому общий элемент должен
стремиться к нулю, то есть ряд расходится.
Примеры
u n 1
(n 1) 2 n 1
n 1 1
n
1. Ряд n сходится, так как lim n u lim n 2 n n 2 lim n n 2 1
n
1
n 1 2
p
2. Рассмотрим ряд
n 1 n
p
u n 1
np
n
1 при n независимо от величины показателя p.
un
(n 1) p n 1
При p=1 – гармонический ряд (расходится);
При p=2 – ряд обратных квадратов (сходится).
Следовательно, при 1 - признак Даламбера не действует.
3. Радикальный признак Коши.
Рассмотрим без доказательства еще один достаточный признак сходимости
знакоположительного ряда.
Рассмотрим ряд u1 u 2 ... u n ...(u n 0) (*)

17.

Если при n существует lim n n u n , то при 1- ряд сходится;
1 - ряд расходится; 1 - радикальный признак Коши не действует.
1
1
1
1
2 ... n
... сходится, так как lim n n n 1
lim n
Пример. Ряд
ln 2 ln 3
ln (n 1)
ln (n 1)
ln( n 1)
4. Интегральный признак Коши
Не трудно заметить полную аналогию определений сходимости ряда и
сходимости несобственного интеграла с бесконечным верхним пределом.
Много общего и в признаках сходимости рядов с положительными
элементами и интегралов с положительной подынтегральной функцией.
Рассмотрим признак, позволяющий в некоторых случаях сводить вопрос о с
ходимости ряда, к вопросу о сходимости интеграла.
Рассмотрим ряд u1 u2 ... un ...(un 0) (*), элементы которого являются
значениями непрерывной положительной функции f(x) при целых значениях
аргумента х: u1 f (1), u 2 f (2),..., u n f (n),.... и пусть f(x) монотонно убывает в
[1, ). Тогда ряд сходится, если сходится несобственный интеграл
интервале
f ( x ) dxи расходится, если этот интеграл расходится.
1
0

18.

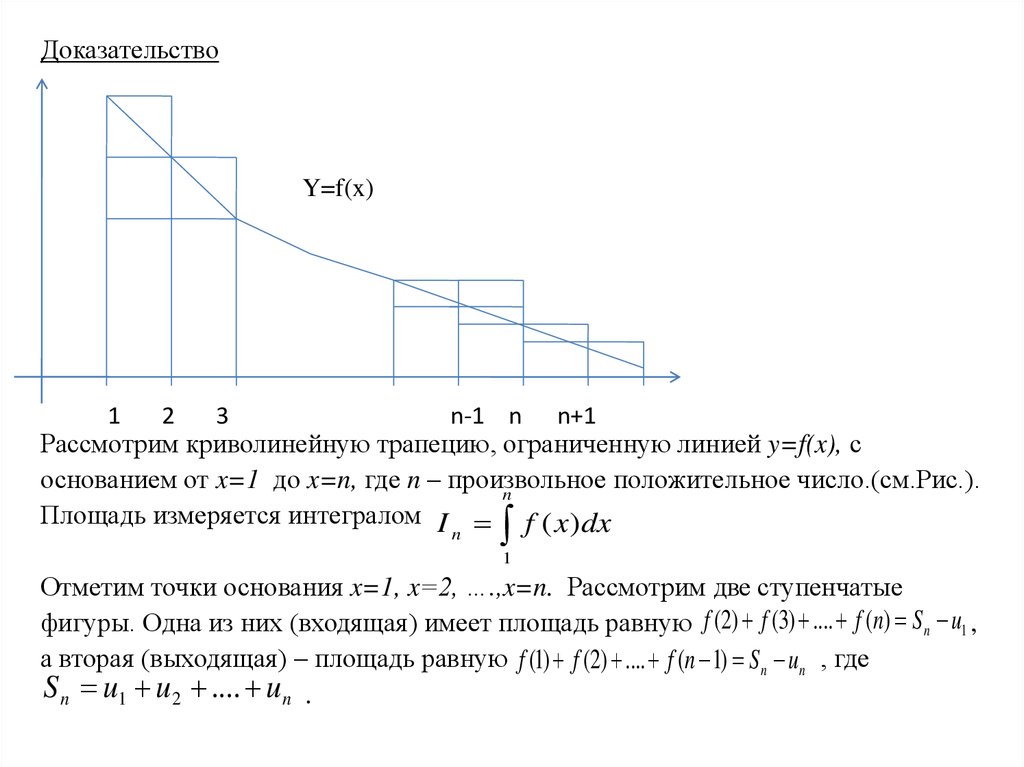
Доказательство
Y=f(x)
1
2
3
n-1 n
n+1
Рассмотрим криволинейную трапецию, ограниченную линией y=f(x), с
основанием от x=1 до x=n, где n – произвольное
положительное число.(см.Рис.).
n
Площадь измеряется интегралом I f ( x ) dx
n
1
Отметим точки основания x=1, x=2, ….,x=n. Рассмотрим две ступенчатые
фигуры. Одна из них (входящая) имеет площадь равную f (2) f (3) .... f (n) S n u1 ,
а вторая (выходящая) – площадь равную f (1) f (2) .... f (n 1) S n un , где
S n u1 u 2 .... u n .

19.

Для представленных площадей справедливо S n u1 I n S n u n
Отсюда получаем два неравенства:
S n I n u1 (1) S n I n u n (2)
Так как f(x)>0, то I n возрастает вместе с n. Возможны два случая:
1) Несобственный интеграл сходится, то есть I lim n I n существует, тогда
I n I и из неравенства (1) при всяком n находим S n I u1 , то есть S n ограничена, тогда на основании леммы ряд сходится.
2) Интеграл расходится: тогда I n при n и на основании
неравенства (2) следует, что S n , то есть ряд расходится.
Пример
1
1
1
1
...
...
p
p
p
Рассмотрим ряд
Для этого ряда признак Даламбера не
n
2
n
n 1
u n 1
применим, так как u 1
n
1
Применим интегральный признак. Подынтегральная функция f ( x) p .
x
1
x p 1
Соответственно интеграл x p dx p 1
1
1
1
lim x ( x p 1 1)
1 p

20.

Если p>1, то lim x x
p 1
0
1
dx
1
p 1
xp
- интеграл сходится.
Если p<1, то интеграл расходится, так как lim x x p 1
При p=1 интеграл также расходится: 1 dx ln x |
1
1 x
В итоге получаем:
При p>1 – ряд сходится
При p<1 – ряд расходится
Геометрическую идею, лежащую в основе доказательства интегрального
признака Коши, можно применить для оценки ошибки, возникающей при
приближенном вычислении суммы ряда, сходимость которого была
установлена с помощью этого признака. Для этого нужно уметь оценивать
величину разности S S n ,то есть остаток ряда rn u n 1 u n 2 ... .
S S n 0 при любом n.
Приведенный рисунок показывает, что остаток ряда есть сумма “уходящих
вправо” прямоугольников и она меньше, чем площадь заключающей их
фигуры, поэтому:
rn
f ( x)dx
n

21.

Применим эту формулу для оценки остатка только, что рассмотренного ряда
1
1
1
p 1 p ... p ... при p>1.
n 1
n
2
rn
n
n
x p 1
f ( x)dx
p 1
n
1
( p 1)n p 1
Если необходимо, чтобы величина остатка ряда не превышала заранее
выбранного числа , то за номер n можно взять наименьшее целое число ,
удовлетворяющее неравенству:
1
p 1
( p 1)n
Пусть p 2; 0,001 1 0,001 n 1000 - это медленно сходящийся ряд.
n
Пусть p 3; 0,001
1
0,001 n 24 - это ряд обратных кубов.
2n 2
Пусть p 4; 0,001
1
0,001 n 7 - быстро сходящийся ряд.
3
3n

22.

Ряды с произвольными элементами. Абсолютная сходимость
Знакочередующиеся ряды
Знакочередующийся ряд можно записать в таком виде: (u1 u 2 u3 ...) (*),
где u1 , u 2 , u3 ,... - положительные числа.
Достаточный признак сходимости – признак Лейбница
Если в знакочередующемся ряду абсолютные величины элементов ряда
убывают, то есть в ряде (*) u1 u 2 u3 ... и общий элемент u n 0 , то
ряд сходится, причем его сумма по абсолютной величине меньше u1 ;
остаток ряда rn по абсолютной величине меньше абсолютной величины
первого из отбрасываемых элементов rn u n 1 .
Доказательство
Возьмем для определенности перед всем рядом (*) знак плюс
u1 u 2 ... u 2 m u 2m 1 ...
Рассмотрим сначала последовательность частичных сумм с четными
индексами и запишем их в виде S 2m (u1 u 2 ) (u3 u 4 ) ... (u 2m 1 u 2m )

23.

Так как по условию выражение в каждой скобке положительно и число таких
скобок растет вместе с m, то последовательность S 2 m будет возрастающей.
Наоборот, последовательность частичных сумм с нечетными индексами
будет убывающей, так как S 2m 1 u1 [(u 2 u3 ) (u 4 u5 ) ... (u 2m u 2m 1 ) и сумма в
квадратной скобке, на основании только, что высказанных соображений,
будет возрастать вместе с m.
Таким образом S 2 S 4 S 6 ... и S1 S 3 S 5 ...
Легко заметить, что любая сумма с четным индексом меньше любой суммы с
нечетным индексом: S 2 m S 2 k 1
Действительно, если m<k, то S 2m S 2k S 2k 1 u 2k 1 S 2k 1
Если же m k , то S 2m S 2 m 1 u 2 m 1 S 2 m 1 S 2 k 1
На следующем рисунке показано геометрическое изображение
последовательности частичных сумм
S2 ; S4 ; S6
S
S 5 ; S 3 ; S1 u1

24.

Последовательность сумм с четными индексами возрастает и ограничена
сверху: значит, она имеет предел lim n S 2 m S
Так как S 2m 1 S 2m u 2m 1 ; lim m u 2m 1 0 lim m S 2m 1 lim m S 2m S , то есть
суммы с нечетными индексами, убывая, стремятся к тому же пределу S.
На рисунке ясно видно, что частичные суммы, приближаясь к своему пределу,
будут по очереди то больше его, то меньше: ясно также, что сумма ряда S
меньше любой суммы с нечетным индексом и в частности меньше u1 .
Если бы перед всем рядом (*) стоял знак минус, то рисунок надо было бы
симметрично отобразить относительно начала координат: в этом случае было
бы | S | u1 .
Остаток ряда rn (u n 1 u n 2 ...) представляет собой ряд, удовлетворяющий
всем условиям признака Лейбница. Поэтому сумма rn по абсолютной
величине меньше первого элемента в скобке, то есть rn u n 1 . Теорема
доказана.
Пример
1 1 1
( 1) n
Ряд 1 ...
... сходится, так как он удовлетворяет всем условиям
2 3 4
n
признака Лейбница.

25.

Абсолютная сходимость
Для рядов с произвольным распределением знаков рассмотрим следующий
достаточный признак сходимости.
Если ряд, составленный из абсолютных величин данного ряда,
сходится, то сходится и данный ряд.
Доказательство
S n сумма первых n элементов ряда;
S n сумма всех положительных среди первых n элементов ряда;
S n сумма абсолютных величин всех отрицательных среди первых n
элементов ряда;
n сумма абсолютных величин всех первых n элементов ряда;
Тогда имеет место S n S n S n и n S n S n
Так как по условию n имеет предел (обозначим ),а S n и S n -положительные
и возрастающие функции от n, причем,S n n и S n n , то они имеют
пределы.
Поэтому S n S n S n при n стремится к пределу. Теорема доказана.

26.

Это достаточный признак не является необходимым, то есть ряд
сходиться, а ряд | u n | - расходится.
n 1
Пример
1 1 1
( 1) n
1 ...
... - сходится
2 3 4
1
u
n 1
n
может
n
1 1
1
... ... - расходится (ряд из абсолютных величин –гармонический
2 3
n
ряд)
Определение
Ряд, абсолютные величины элементов которого образуют сходящийся ряд,
называется абсолютно сходящимся.
Если ряд сходится, а ряд образованный из абсолютных величин его
элементов, расходится, то данный ряд называется условно сходящимся ( не
абсолютно).
1 1 1
( 1) n
Например 1 ...
... - условно сходящийся.
2 3 4
n

27.

Указанное разграничение абсолютной и условной сходимостей рядов
является весьма существенным.
Оказывается, что некоторые свойства конечных сумм переносятся только
на абсолютно сходящиеся ряды; условно сходящиеся этими свойствами не
обладают.
Так абсолютно сходящиеся ряды обладают переместительным свойством
(при любой перемене мест элементов абсолютно сходящихся рядов он
остается абсолютно сходящимся и с той же суммой). Это свойство отсутствует
у условно сходящихся рядов. Оказывается, переставляя элементы такого ряда,
можно добиться того, что сумма ряда изменится.
Пример
1 1 1
( 1) n
Рассмотрим ряд 1 ...
... и переставим элементы ряда таким
2 3 4
n
1 1 1 1 1
образом 1 ... Сложим каждый положительный элемент с
2 4 3 6 8
1 1 1 1
идущим после него отрицательным: ... В результате получим
2 4 6 8
ряд, элементы которого образованы произведениями элементов исходного
1
ряда на величину .
2

28.

1
Но такой ряд по свойству 1 также сходится и его сумма равна суммы
2
исходного ряда.
Абсолютно сходящиеся ряды можно перемножать
Определение
Под произведением двух сходящихся рядов
S ' u1 u2 ... un ... (1)
S ' ' v1 v2 ... vn ... (2)
Понимается следующий ряд
(u1 v1 ) (u1 v2 u 2 v1 ) (u1 v3 u 2 v2 u3 v1 ) ... (u1 vn u 2 vn 1 ... u n 1 v2 u n v1 ) (3)
В каждой группе элементов этого ряда, объединенных скобками, сумма
индексов сомножителей постоянна: в первой – 2; во второй – 3; … ; в n – ой –
(n+1)
Теорема ( без доказательства)
Если ряды (1) и (2) абсолютно сходятся, то их произведение есть также
абсолютно сходящийся ряд, сумма которого равна произведению сумм рядов
сомножителей

29.

Функциональные ряды
Ряд, элементами которого являются функции, называется
функциональным рядом. Обозначение:
u1 ( x) u 2 ( x) ... u n ( x) ... (*), где u n (x) - определены и непрерывны в одном и
том же интервале.
Ряд (*) для одних значений х может сходиться, а для других расходиться.
Значение x x0 , при котором числовой ряд u1 ( x0 ) u2 ( x0 ) ... un ( x0 ) ...
сходится, называется точкой сходимости ряда (*).
Совокупность всех точек сходимости ряда называется областью сходимости
ряда, или говорят, что ряд сходится в данной области. Областью сходимости
обычно бывает какой-либо интервал оси ОХ.
Пример
Ряд 1 x x 2 ... x n .. сходится в интервале (-1;1), так как при |x|<1 –
числовой ряд бесконечно убывающая геометрическая прогрессия.
При | x | 1 - ряд расходится.
Сумма ряда является некоторой функцией от х, определенной в области
сходимости ряда.
Обозначение S ( x) u1 ( x) u 2 ( x) ... u n ( x) ...

30.

1
Для приведенного примера S ( x)
, для интервала (-1;1), то есть области
1 x
сходимости ряда.
S n ( x) u1 ( x) u 2 ( x) ... u n ( x) - n –ая частичная сумма;
rn (x) остаток ряда.
Если ряд сходится, то lim n S n ( x) S ( x); lim n rn ( x) 0
Известно, что сумма кончного числа непрерывных функций – функция
непрерывная, и интеграл от такой суммы непрерывных функций равен
сумме интегралов от этих функций. Точно также производная от суммы
конечного числа дифференцируемых функций равна сумме
производных.
Можно ли эти свойства перенести на функциональные ряды?
Покажем, что для произвольных функциональных рядов эти свойства могут
оказаться несправедливыми.
x2
x2
x2
Рассмотрим ряд
...
...
2
2 2
2 n
1 x (1 x )
(1 x )

31.

При х=0 элементы ряда нули и S(0)=0.
1
q
1
При x 0 - ряд сходящаяся
геометрическая прогрессия, так как
2
2
1 x
1
x
1
и сумма ряда S 1 q 1 x 2 : 1 1 x 2 1
Таким образом, S(x) – разрывная функция. Она имеет разрыв в точке х=0, то
есть S(x)=1, если и S(0)=0.
Чтобы установить, в каких же случаях на функциональные ряды можно
перенести свойства конечных сумм, введем новое определение.
Определение
Функциональный ряд u1 ( x) u2 ( x) ... u n ( x) ... (*) называется правильно
сходящимся в области D, принадлежащей области сходимости ряда, если в
области D все его элементы по абсолютной величине не превосходят
соответствующих элементов некоторого числового ряда с положительными
элементами.
Это значит, что во всех точках области D должно выполняться неравенство
u n M n , где M n - элемент сходящегося ряда M 1 M 2 ... M n ... Этот ряд
называется мажорирующим (усиливающим) по отношению к ряду (*).

32.

Пример
sin 2 x sin 3x
sin nx
Ряд sin x 2 2 ... 2 ... правильно сходится в любом интервале оси
2
3
n
sin nx
1
ОХ, так как n 2
n 2 , а ряд обратных квадратов сходящийся.
Свойства правильно сходящихся рядов
Сформулируем основные теоремы о правильно сходящихся рядах, которые
дают ответ на вопрос о переносе на ряды свойств сумм конечного числа
функций. Во всех теоремах предполагается, что область правильной с
ходимости ряда есть некоторый интервал оси ОХ.
Теорема 1
Если ряд из непрерывных функций правильно сходится в области D, то его
сумма есть функция непрерывная в этой области.
Так ряд sin x sin 22 x sin 23x ... sin 2nx ... сходится правильно в любом
2
3
n
интервале. Следовательно, его сумма S(x) – непрерывная функция.
Теорема 2

33.

Теорема 2
Если ряд из непрерывных функций правильно сходится, то интеграл от
суммы
ряда
равен сумме
ряда, составленного
из интегралов от этих функций:
b
b
b
b
a S ( x)dx a u1 ( x)dx a u2 ( x)dx ... a un ( x)dx ... (*)
Короткая формулировка
Правильно сходящийся ряд можно поэлементно интегрировать
Доказательство
Из определения правильной сходимости данного ряда следует, что un ( x) M n ,
где M n - элемент сходящегося числового ряда. По теореме об оценке
b
b
интегралов, имеем: u ( x)dx u ( x) dx M (b a)
a
n
n
n
a
Но ряд с общим элементом M n (b a) сходится, тогда сходится и ряд из
интегралов и даже абсолютно.
Замечание
Теорема 2 справедлива и в том случае, когда берутся интегралы с переменным
верхним
пределом:
x
x
x
x
S ( x)dx u1 ( x)dx u 2 ( x)dx ... u n ( x)dx ... где a x b
a
a
a
a

34.

x
x
Пользуясь оценкой интегралов, имеем u n ( x)dx u n ( x) dx M n ( x a) M n (b a)
a
a
Тогда и данный ряд сходится правильно.
Теорема 3
Если ряд u1 ( x) u 2 ( x) ... u n ( x) ... составленный из функций,
имеющих непрерывные производные, сходится в области D и его сумма равна
'
S(x), а ряд из производных u n ( x ) сходится в этой области правильно, то
производная суммы ряда S’(x) равна сумме ряда из производных:
S ' ( x) u1 ' ( x) u 2 ' ( x) ... u n ' ( x) ...
Короткая формулировка
Если ряд, составленный из производных сходящегося ряда, сходится
правильно, то его можно поэлементно дифференцировать.
Замечание
Правильная сходимость данного ряда, а также дифференцируемость его
суммы не предполагается, а является следствиеми условий теоремы. Однако
проверка правильной сходимости ряда из производных совершенно
обязательна; при невыполнении этого условия теорема может потерять
смысл.

35.

Пример
sin 2 3 x
sin n 3 x
Ряд sin x 2 ... 2 ... правильно сходится (он мажорируется рядом
2
n
обратных квадратов) и его сумма непрерывная функция.
Ряд из производных cos x 2 cos 2 3 x ... n cos n 3 x ... расходится, так как его
общий элемент ни при каком х не стремится к нулю. Следовательно теорем не
применима.