Similar presentations:
Системы эконометрических уравнений
1. Системы эконометрических уравнений
Подготовил: Тягливый А.С.Студент 1 курса Магистерской
подготовки экономика.
2.
• 1. система независимых уравнений (когдакаждая зависимая переменная y
рассматривается как функция одного и того
же набора факторов x)
y1 a11 x1 a12 x2 a1m xm ε1 ,
y a x a x a x ε ,
2
21 1
22 2
2m m
2
yn an1 x1 an 2 x2 anm xm εn .
3.
• Набор факторов в каждом уравненииможет варьироваться. Так, модель вида
y1 f x1 , x2 , x3 , x4 , x5
y2 f x1 , x3 , x4 , x5
y 3 f x 2 , x 3 , x5
y4 f x 3 , x 4 , x 5
• также является системой независимых
уравнений.
4.
• Каждое уравнение системынезависимых уравнений может
рассматриваться самостоятельно. Для
нахождения его параметров
используется метод наименьших
квадратов.
5.
2. системы рекурсивных уравнений:y1 a11 x1 a12 x2 a1m xm 1 ,
y b y a x a x a x ,
2m m
2
2 21 1 21 1 22 2
y3 b31 y1 b32 y2 a31 x1 a32 x2 a3 m xm 3 ,
yn bn1 y1 bn 2 y2 bnn 1 yn 1 an1 x1 an 2 x2 anm xm n .
зависимая переменная включает в каждое
последующее уравнение в качестве факторов все
зависимые переменные предшествующих
уравнений наряду с набором собственно
факторов x.
6.
• Примером такой системы может служить модельпроизводительности труда и фондоотдачи
вида:
y1 a11 x1 a12 x2 a13 x3 1 ,
y 2 b21 y1 a21 x1 a 22 x2 a 23 x3 2
где y1- производительность труда;
y 2 - фондоотдача;
x1 - фондовооруженность труда;
x 2 -энерговооруженность труда;
x3 - квалификация рабочих.
7.
• 3. система взаимозависимых уравнений(системы совместных, одновременных
уравнений ).
y1 b 12 y1 b 13 y3 b 1n yn a 11 x1 a 12 x2 a 1m xm 1 ,
y2 b 21 y1 b 2 3 y3 b 2 n yn a 21 x1 a 22 x2 a 2 m xm 2 ,
y b y b y b y a x a x a x .
n n 1 n 1
n1 1
n2 2
nm m
n
n n1 1 n 2 2
8.
• Пример: модель динамики цены и заработнойплаты вида
y1 b12 y 2 a11 x1 1 ,
y 2 b21 y1 a22 x2 a23 x3 2 ,
• y1
• y2
• x1
• x2
• x3
- темп изменения месячной заработной платы;
- темп изменения цен;
- процент безработных;
- темп изменения постоянного капитала;
- темп изменения цен на импорт сырья.
9.
• В отличие от предыдущих систем каждоеуравнение системы одновременных
уравнений не может рассматриваться
самостоятельно, и для нахождения его
параметров традиционный МНК
неприменим.
10.
• Система совместных, одновременныхуравнений обычно содержит эндогенные
и экзогенные переменные.
• Эндогенные переменные (y). Это
зависимые переменные, число которых
равно числу уравнений в системе.
• Экзогенные переменные (x). Это
предопределенные переменные,
влияющие на эндогенные переменные,
но не зависящие от них.
11.
• структурные коэффициенты модели:bi
- коэффициент при эндогенной
переменной,
a j - коэффициент при экзогенной
переменной
12.
• для определения структурных коэффициентовмодели структурная форма модели
преобразуется в приведенную форму модели.
• Приведенная форма модели представляет
собой систему линейных функций эндогенных
переменных от экзогенных:
yˆ 1 11 x1 12 x 2 1m x m ,
yˆ x x x ,
2
21
1
22
2
2m
m
yˆ n n1 x1 n 2 x 2 nm x m ,
• i -коэффициенты приведенной формы модели.
13.
• Пример:• Для структурной модели вида
y1 b12 y2 a11 x1 ,
y2 b21 y1 a22 x2 .
• приведенная форма модели имеет вид
y1 11 x1 12 x2 ,
y2 21 x1 22 x2 .
14.
• из первого уравнения получаем:y1 a11 x1
y2
.
b12
• Тогда система одновременных
уравнений будет представлена как
y1 a11 x1
,
y2
b12
y b y a x .
21
1
22
2
2
15.
• Отсюда имеем:y1 a11 x1 b12b21 y1 b12a22 x2
y1 b12b21 y1 a11 x1 b12a22 x2
a11
b12a22
y1
x1
x2
1 b12b21
1 b12b21
16.
• Таким образом, мы представили первоеуравнение структурной формы модели в
виде уравнения приведенной формы
модели:
y1 11 x1 12 x2 .
• Отсюда
a11
11
1 b12b21
b12a 22
12
x2 .
1 b12b21
17.
• Аналогично получаем:a11b21
21
1 b12b21
a 22
22
.
1 b12b21
18.
• Проблема идентификации.• Идентификация - единственность
соответствия между приведенной и
структурной формами модели.
19.
• С позиции идентифицируемостиструктурные модели можно
подразделить на три вида:
идентифицируемые;
неидентифицируемые;
сверхидентифицируемые.
20.
• Модель идентифицируема, если всеструктурные ее коэффициенты определяются
однозначно, единственным образом по
коэффициентам приведенной формы модели,
т. е. если число параметров структурной
модели равно числу параметров
приведенной формы модели.
21.
• Модель неидентифицируема, если числоприведенных коэффициентов меньше числа
структурных коэффициентов, и в результате
структурные коэффициенты не могут быть
оценены через коэффициенты приведенной
формы модели.
22.
• Модель сверхидентифицируема, есличисло приведенных коэффициентов
больше числа структурных
коэффициентов. В этом случае на основе
коэффициентов приведенной формы
можно получить два или более значений
одного структурного коэффициента.
23.
• обозначим• H -число эндогенных переменных в j – м
уравнении системы,
• D - число экзогенных переменных, которые
содержатся в системе, но не входят в данное
уравнение,
• то условие идентифицируемости модели
может быть записано в виде:
—уравнение идентифицируемо;
— уравнение неидентифицируемо;
— уравнение сверхидентифицируемо.
24.
• Модель считается идентифицируемой, есликаждое уравнение системы
идентифицируемо.
• Если хотя бы одно из уравнений системы
неидентифицируемо, то и вся модель
считается неидентифицируемой.
• Сверхидентифицируемая модель содержит
хотя бы одно сверхидентифицируемое
уравнение.














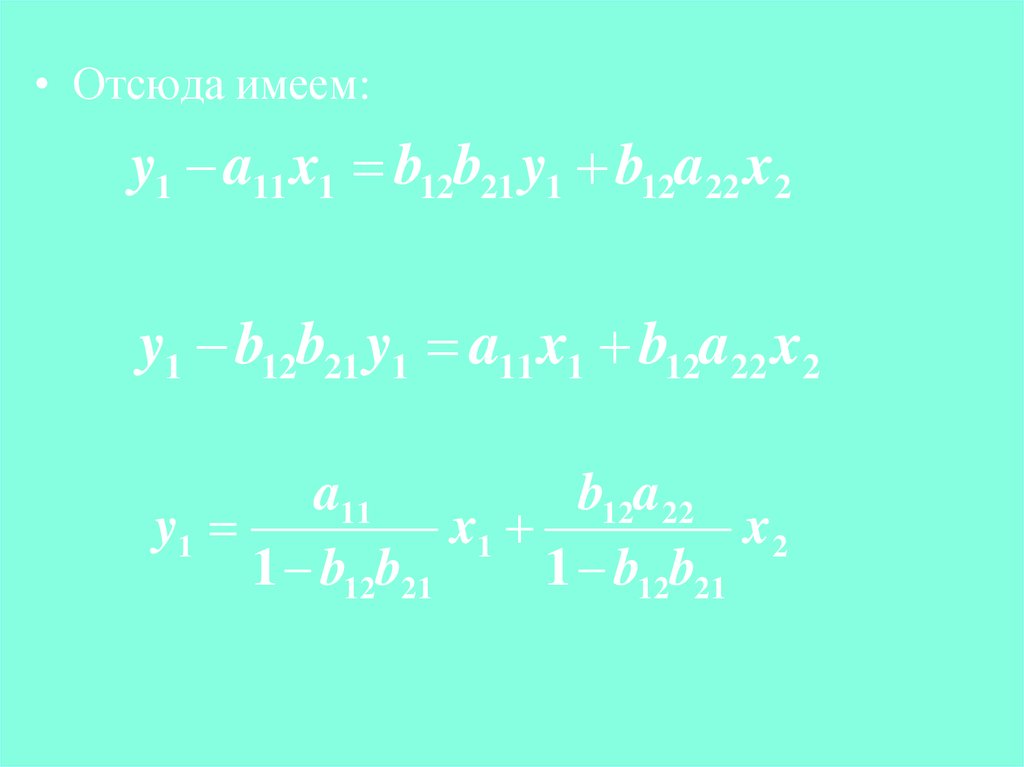










 mathematics
mathematics








