Similar presentations:
Задачи в координатах II
1.
9 класс2.
Содержание1. Радиус-вектор
2. Связь между координатами вектора и
координатами его начала и конца
3. Координаты середины отрезка
4. Вычисление длины вектора по его координатам
5. Расстояние между двумя точками
3.
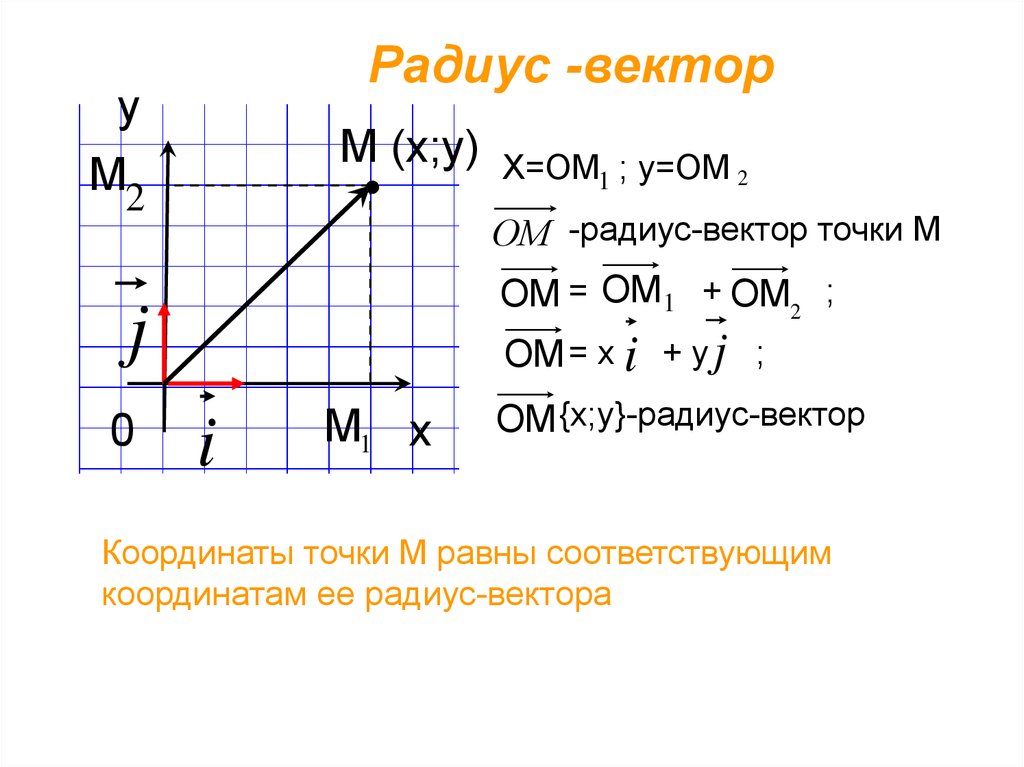
Радиус -вектору
М (х;у)
М2
ОМ -радиус-вектор точки М
ОМ = ОМ1 + ОМ2 ;
j
0
Х=ОМ1 ; у=ОМ 2
ОМ = х i + у j ;
i
М1 х
ОМ {х;у}-радиус-вектор
Координаты точки М равны соответствующим
координатам ее радиус-вектора
4.
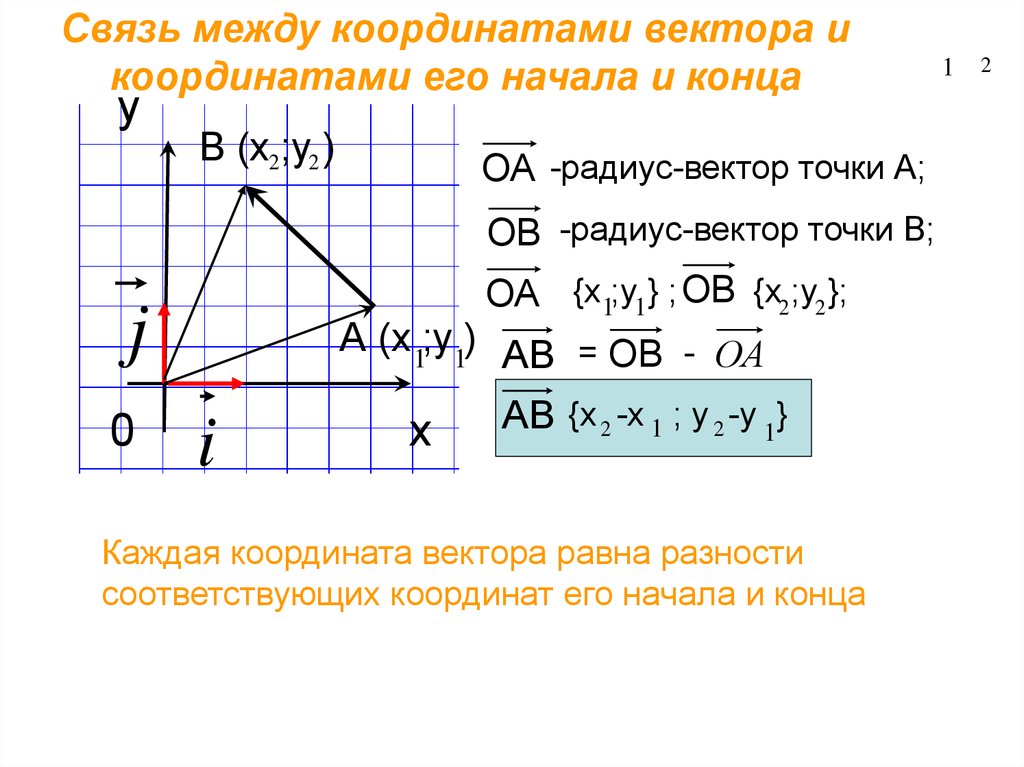
Связь между координатами вектора икоординатами его начала и конца
у
В (х2 ;у2 )
ОВ -радиус-вектор точки В;
ОА {х1;у1} ; ОВ {х2 ;у2 };
j
0
ОА -радиус-вектор точки А;
А (х 1;у1) АВ = ОВ - ОА
i
х
АВ {х 2 -х 1 ; у 2 -у 1}
Каждая координата вектора равна разности
соответствующих координат его начала и конца
1 2
5.
Координаты середины отрезкау
А (х 1;у1)
С-середина отрезка АВ;
С (х;у)
В (х2 ;у 2)
1
1
(ОВ ОА ) ( х1; у1 х 2 ; у 2 );
2
2
х1 х 2 у1 у 2
х1 х 2 у1 у 2
; С
.
ОС
;
;
2
2
2
2
ОС
2
0
х
х
х1 х 2
у у2
;у 1
.
2
2
Каждая координата середины отрезка равна
полусумме соответствующих координат его концов
6.
Длина векторау
С (х;у)
С2
ОС ОС С1С ;
2
1
ОС1 х; С1С ОС 2 у;
ОС х у
2
0
2
С
1
х
2
7.
Расстояние между двумя точкамиу
А (х 1;у1)
АВ х 2 х 1; у2 у1 ;
АВ
В (х2 ;у2)
0
х
х 2 х 1 2 у2 у1 2 ;
АВ АВ
х 2 х 1 2 у2 у1 2 .
8.
9.
10. Проверь свои знания
• Что такое радиус-вектор точки?• Как вычислить координаты вектора по
координатам его начала и конца?
• Как вычислить координаты середины
отрезка по координатам его начала и
конца?
• Как найти длину отрезка по его
координатам?
• Как вычислить расстояние между двумя
точками по их координатам?








 mathematics
mathematics








