Similar presentations:
Электронные процессы в твердом теле. Оптические явления в твердом теле
1.
Физическаяэлектроника
2. Электронные процессы в твердом теле Оптические явления в твердом теле
3.
ПетроваОльга Борисовна
petrova@proriv.ru
8-903-201-65-98
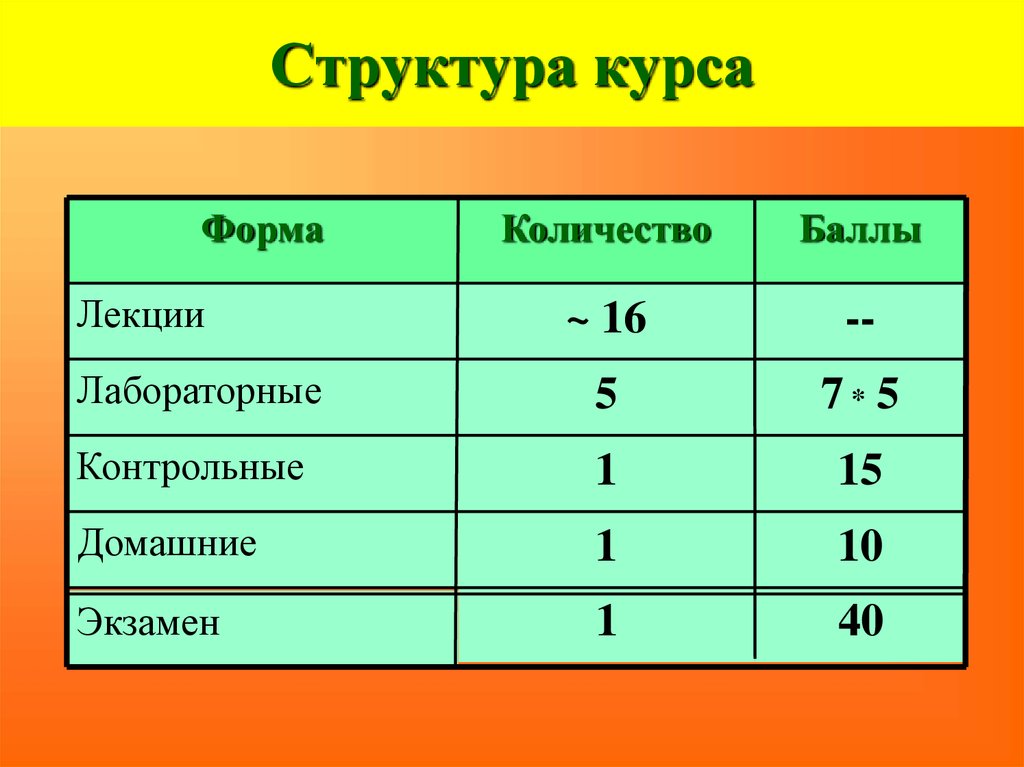
4. Структура курса
ФормаКоличество
Баллы
~ 16
--
Лабораторные
5
7* 5
Контрольные
1
15
Домашние
1
10
Экзамен
1
40
Лекции
5. Основные направления курса
• Элементы зонной теории твердыхтел
• Полупроводники, генерация и
движение носителей тока
• Сверхпроводники
• Диэлектрические материалы
• Магнитные материалы
• Электронные и ионные явления в
газах, газовые разряды
6. Основные направления курса
Начальные сведения о технике СВЧ
Фотоэлектрические приборы
Люминесценция
Лазеры
Волоконная оптика
Новые и перспективные
направления в электронике
7.
Элементы зонной теории твердыхтел
Зонная теория базируется на
принципах квантовой механики:
принцип квантования
принцип неопределённости
Гейзенберга
принцип несовместимости Паули
8. Специфические допущения:
1)разделение частиц кристалла на
лёгкие и тяжёлые - на валентные
электроны и ионы.
9. Специфические допущения:
В равновесии,We Wi
me V
M i Vi
2
2
2
e
2
2
e
2
i
V
Mi
V
me
M i 1800me
Ve
Mi
1800 40
Vi
me
10. Специфические допущения:
1) разделение частиц кристалла на лёгкие итяжёлые - на валентные электроны и
ионы.
= > не рассматриваем: обмен энергиями
движения ионов и электронов
=>
система электронов изолированная
«адиабатическое приближение»
11. Специфические допущения:
2 ) пренебрежение всеми процессами вкристаллах, сопровождающимися
конечным смещением ионов
= > не рассматриваем:
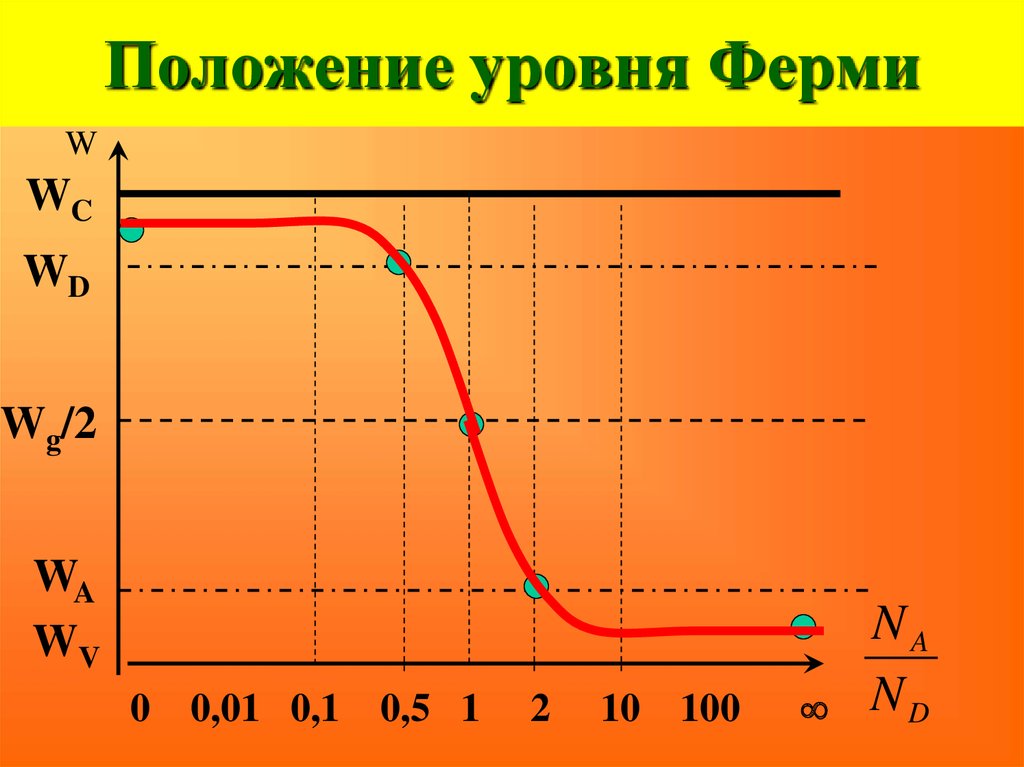
фазовые превращения,
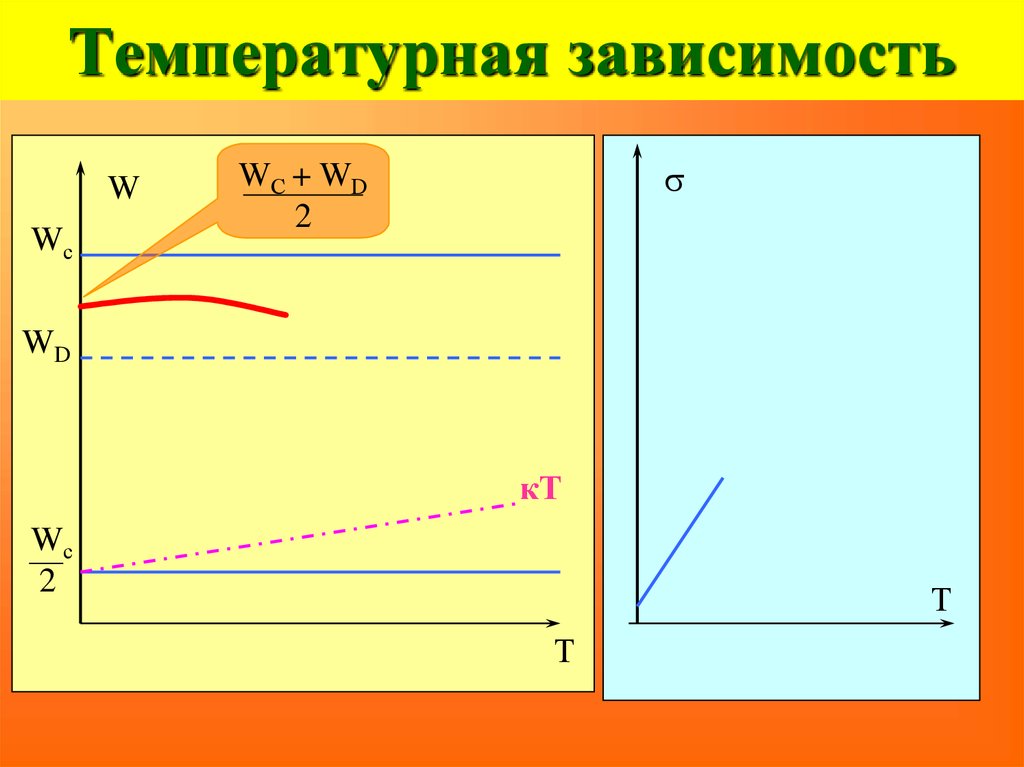
процессы с изменением ионной
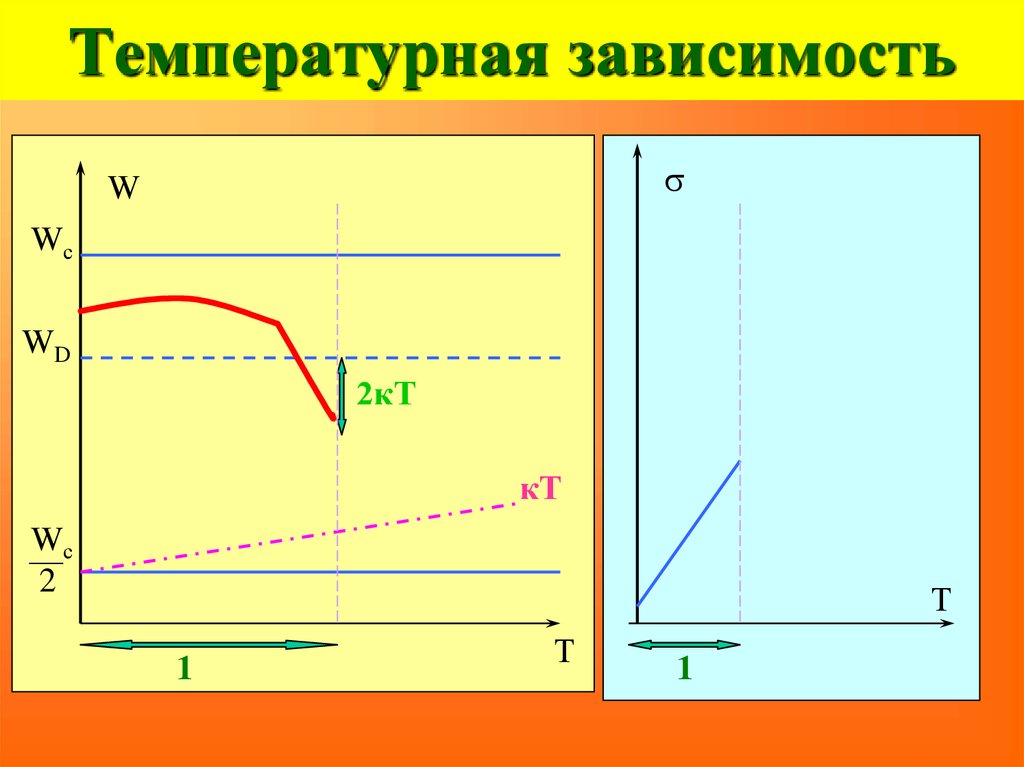
конфигурации
12. Специфические допущения:
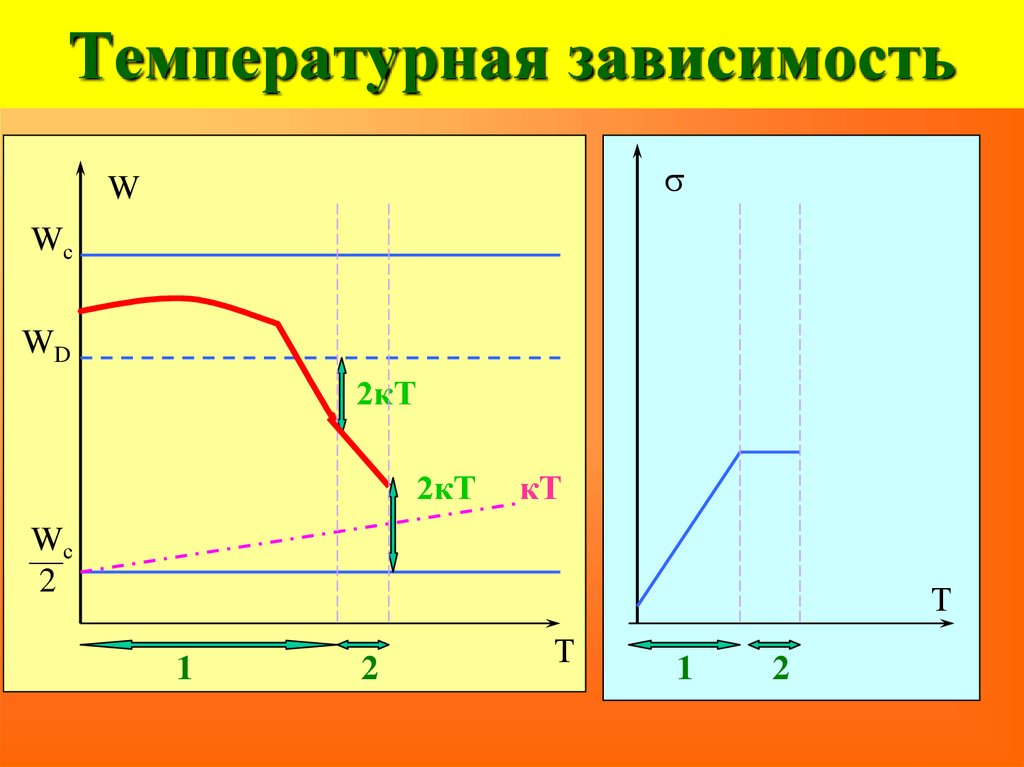
3 ) сведение задачи многих тел кодноэлектронной задаче.
Взаимодействие каждого электрона со всеми
остальными заменяется действием
стационарного поля, создаваемого ансамблем
электронов, на единичный, выбранный для
рассмотрения, электрон.
13. Специфические допущения:
3 ) сведение задачи многих тел кодноэлектронной задаче.
Решение для газов было выполнено Хартри.
При этом использовалось распределение Максвелла.
Уточнения в уравнения Хартри, налагаемые
статистикой Ферми, были внесены Фоком.
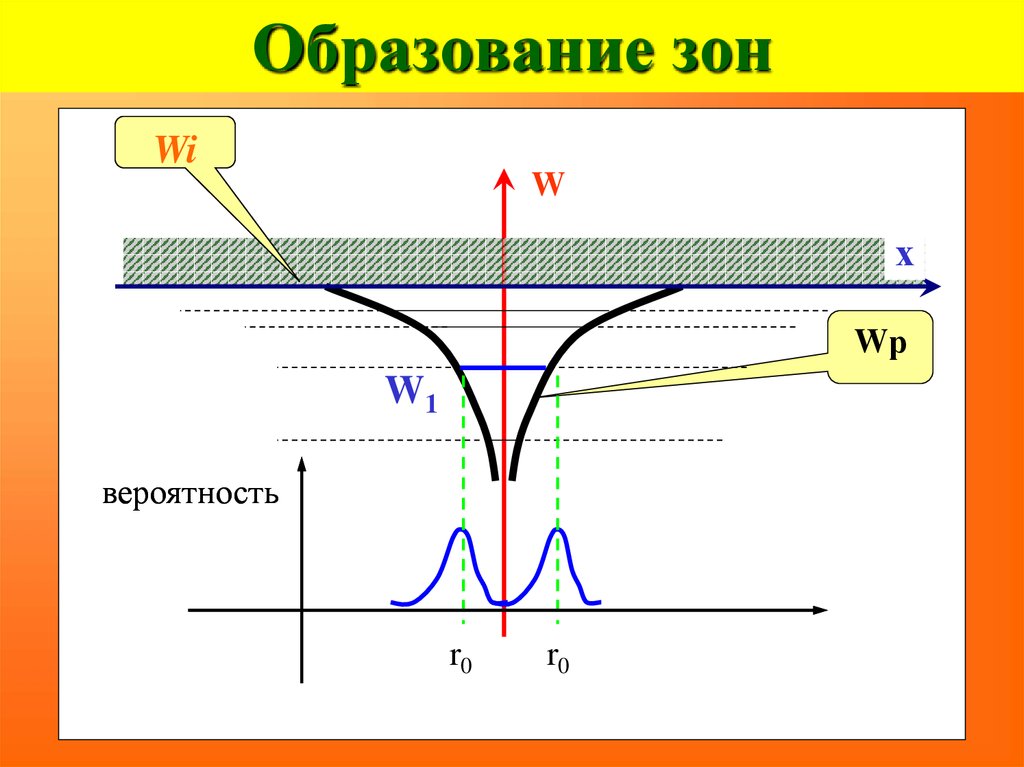
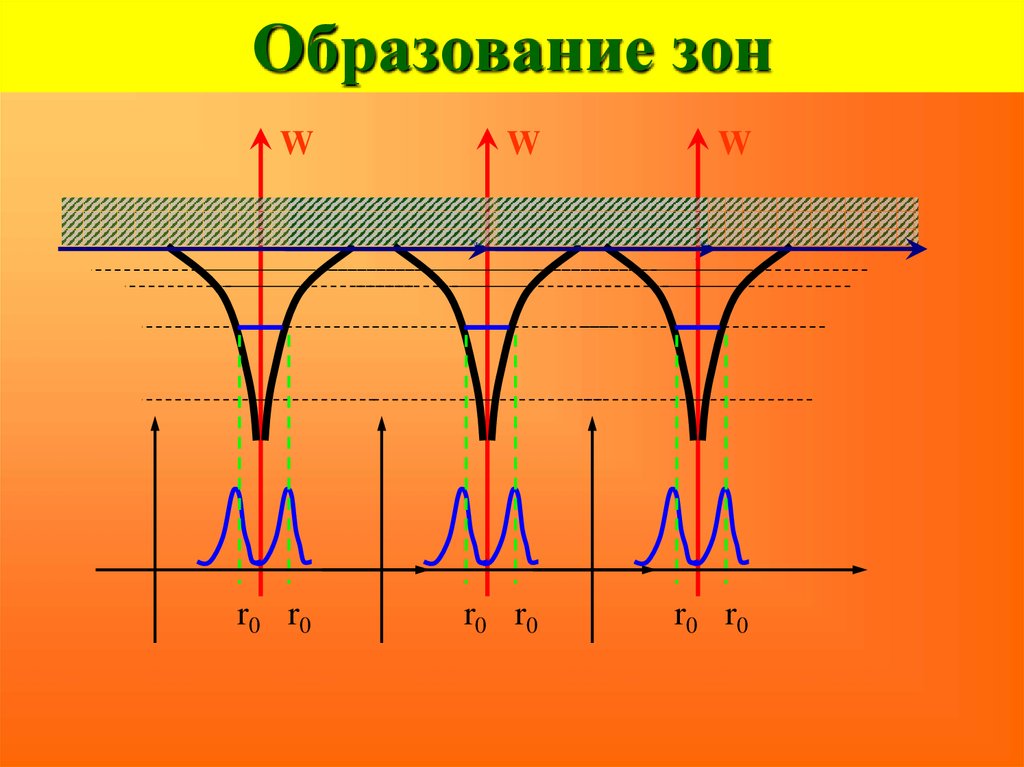
14. Образование зон
WiW
х
Wр
W1
вероятность
r0
r0
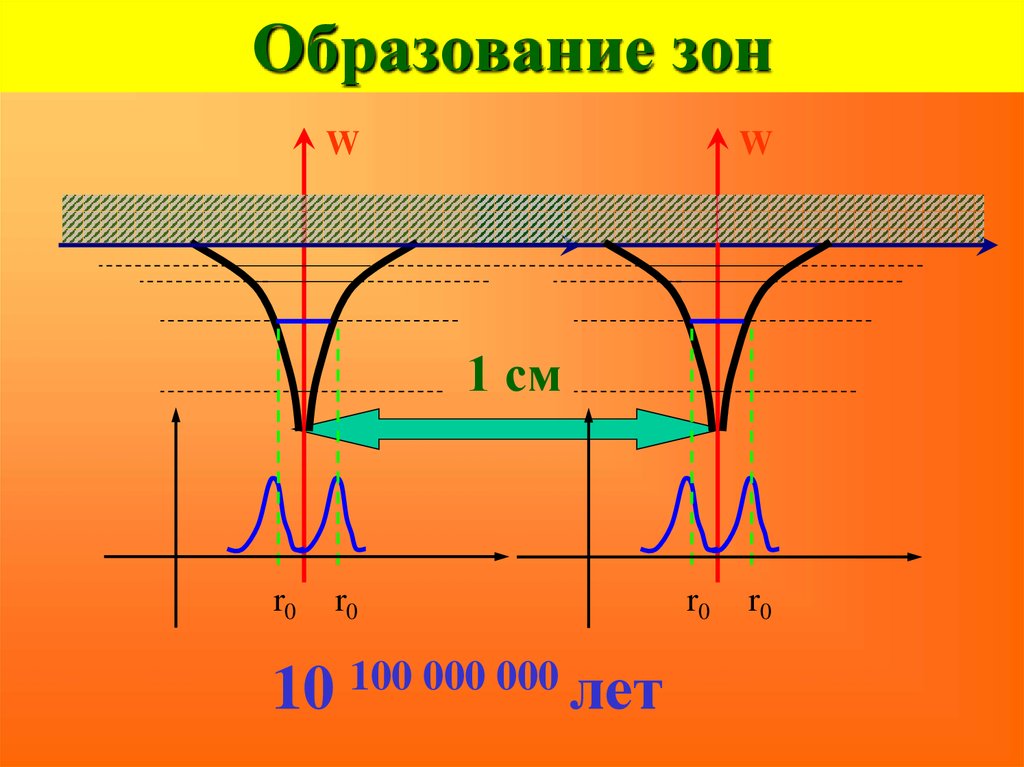
15. Образование зон
WW
1 см
r0
r0
10 100 000 000 лет
r0
r0
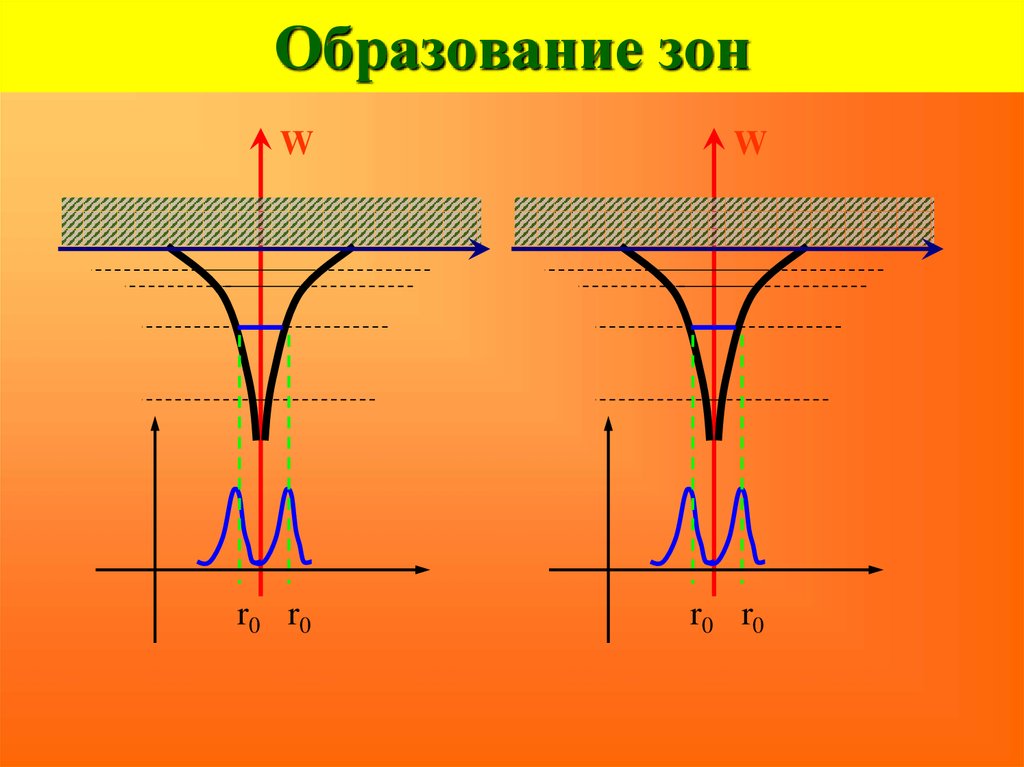
16. Образование зон
WW
r0 r0
r0 r0
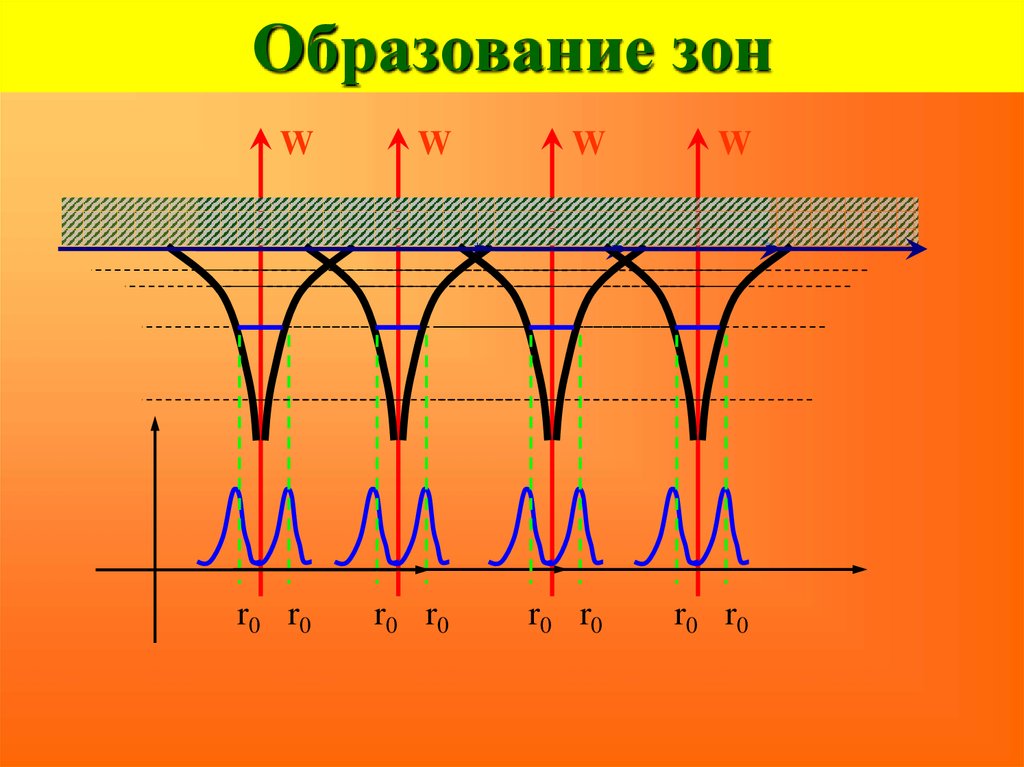
17. Образование зон
WW
W
r0 r0
r 0 r0
r0 r0
18. Образование зон
WW
W
W
r0 r0
r0 r0
r0 r0
r0 r0
19. Образование зон
Wвероятность
W
10-8 см
10 –15 с
W
W
20. Образование зон
Расщепление уровней обусловлено принципомнеопределённости Гейзенберга:
ΔW· τ ≥ ħ
время возбужденного состояния
электрона в отдельном атоме
время нахождения валентного
10-8 с
электрона около каждого иона в кристалле
10–15 с
ΔW = ħ/τ
(ħ = 6,583 10-16 эВ с)
ΔW ~ 10-8 эВ с
Уровни в кристалле ΔW ~ 1 эВ с
Уровни в атоме
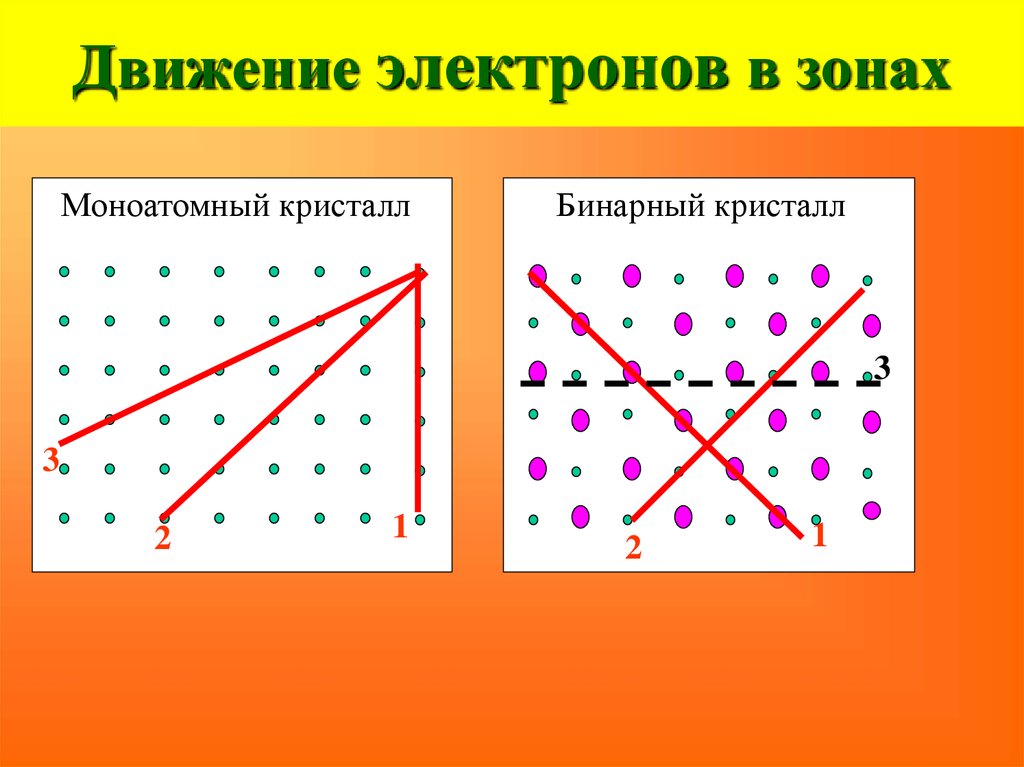
21. Движение электронов в зонах
Моноатомный кристаллБинарный кристалл
3
3
2
1
2
1
22. Движение электронов в зонах
масса свободного электронаэффективная масса
- m
- m*
Причины изменения m*
1. периодическое электрическое поле решётки
2. вектор силы внешнего поля не обязательно
совпадает с направлением разрешённого
движения электрона.
3. ширина зоны: более узких зонах обычно и
большая величина m*.
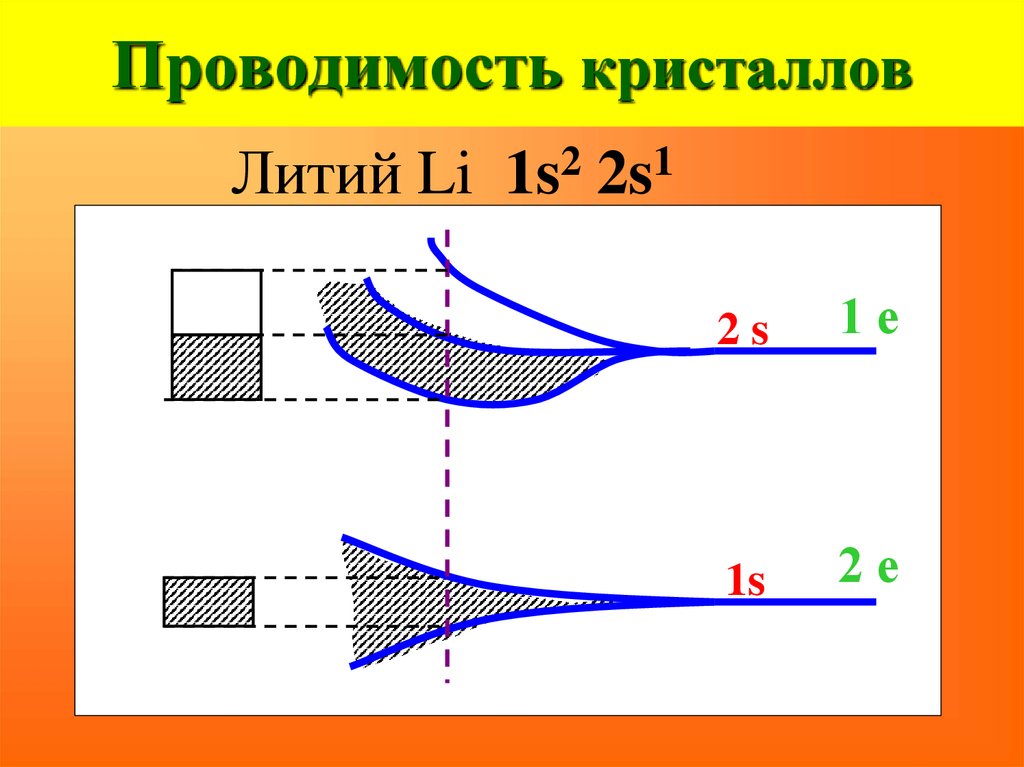
23. Проводимость кристаллов
Литий Li1s2 2s1
2s
1е
1s
2е
24. Проводимость кристаллов
Литий Li2
1s
1
2s
2s
1е
1s
2е
25. Проводимость кристаллов
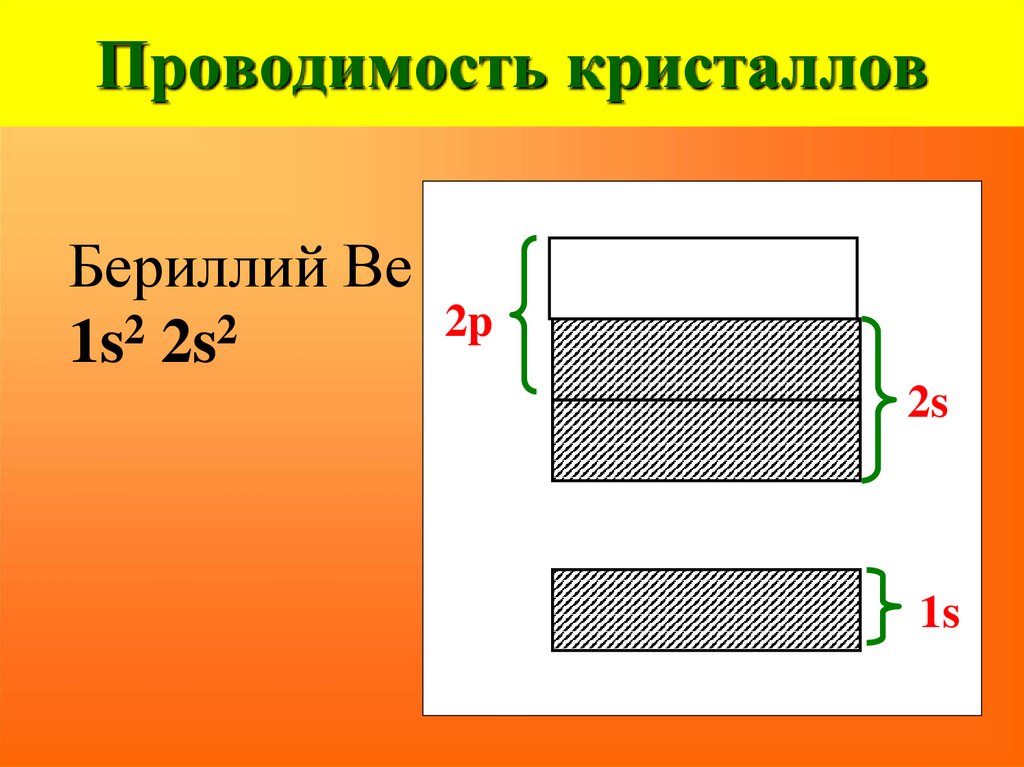
Бериллий Ве1s2 2s2
2p
2s
1s
26. Проводимость кристаллов
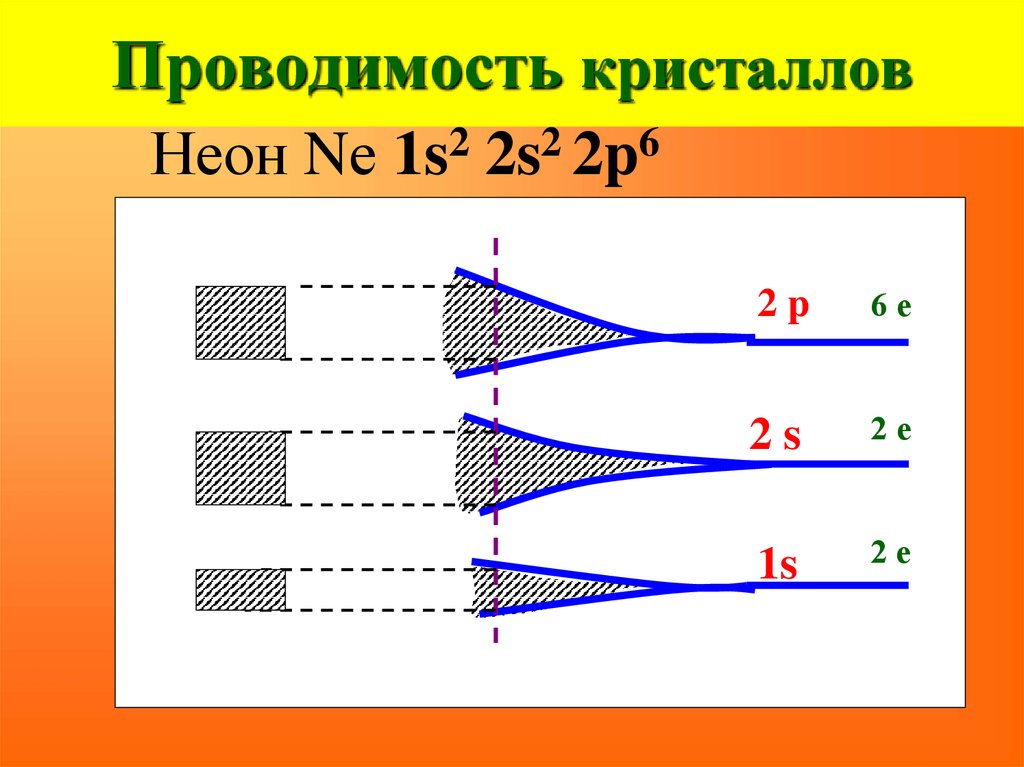
Неон Nе 1s2 2s2 2p62p
6е
2s
2е
1s
2е
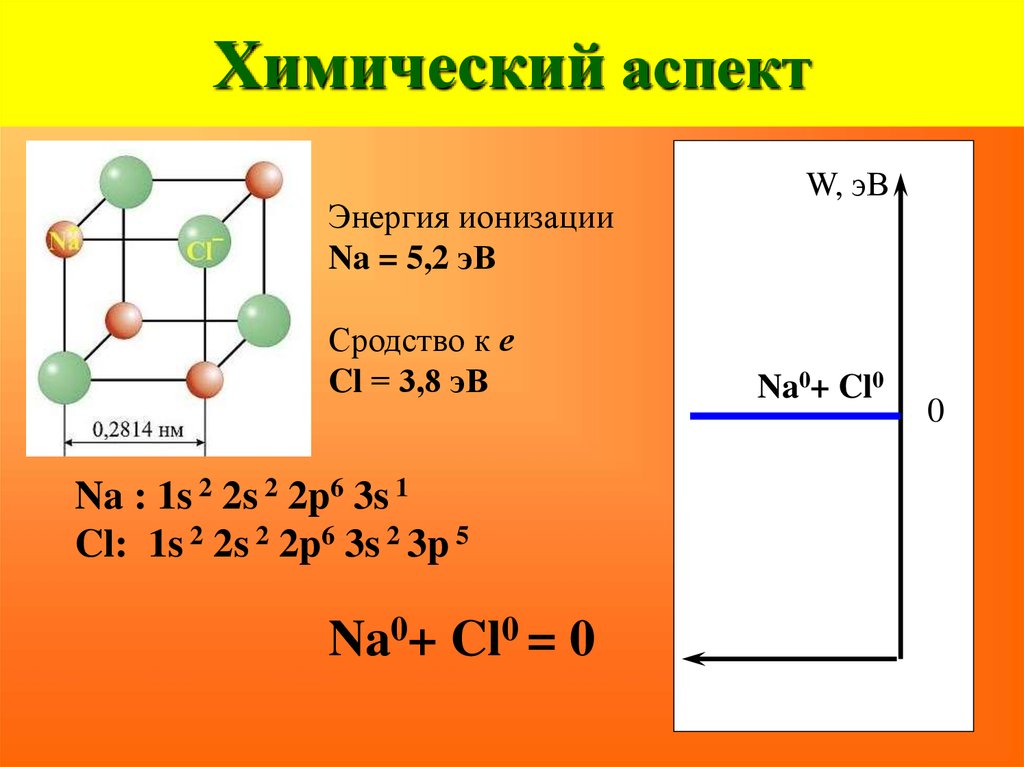
27. Химический аспект
Энергия ионизацииNa = 5,2 эВ
Сродство к е
Cl = 3,8 эВ
Na : 1s 2 2s 2 2p6 3s 1
Cl: 1s 2 2s 2 2p6 3s 2 3p 5
Na0+ Cl0 = 0
W, эВ
Na0+ Cl0
0
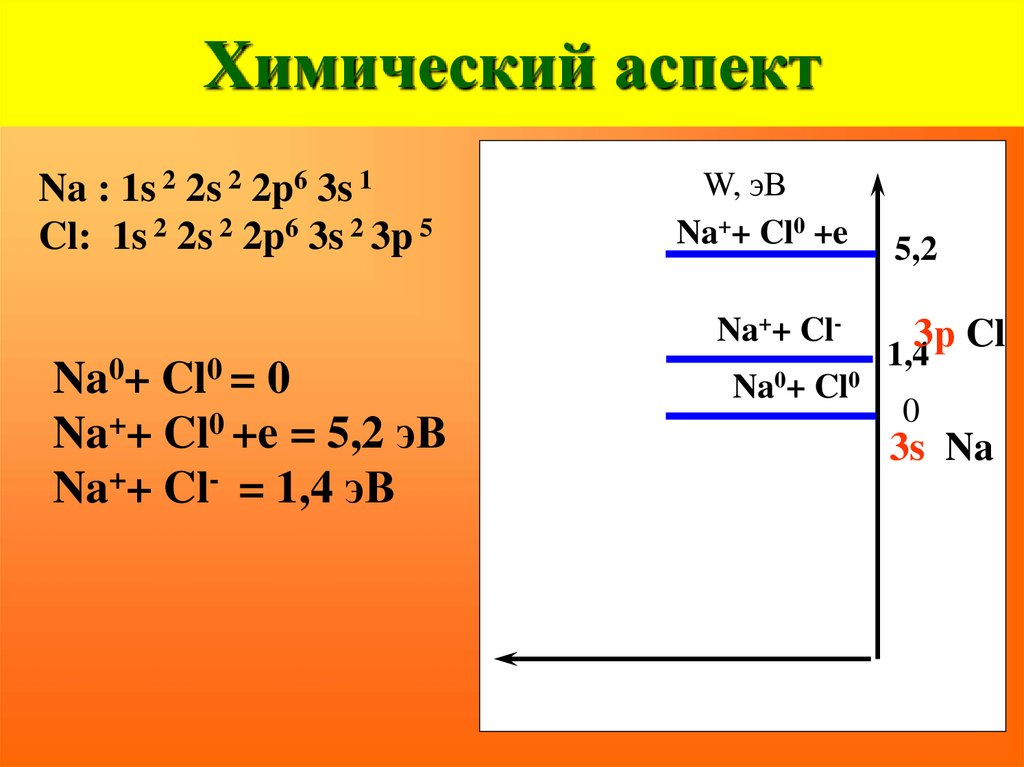
28. Химический аспект
Na : 1s 2 2s 2 2p6 3s 1Cl: 1s 2 2s 2 2p6 3s 2 3p 5
Энергия ионизации Na = 5,2 эВ
Сродство к е Cl = 3,8 эВ
Na0+ Cl0 = 0
Na++ Cl0 +e = 5,2 эВ
W, эВ
Na++ Cl0 +e 5,2
Na0+ Cl0
0
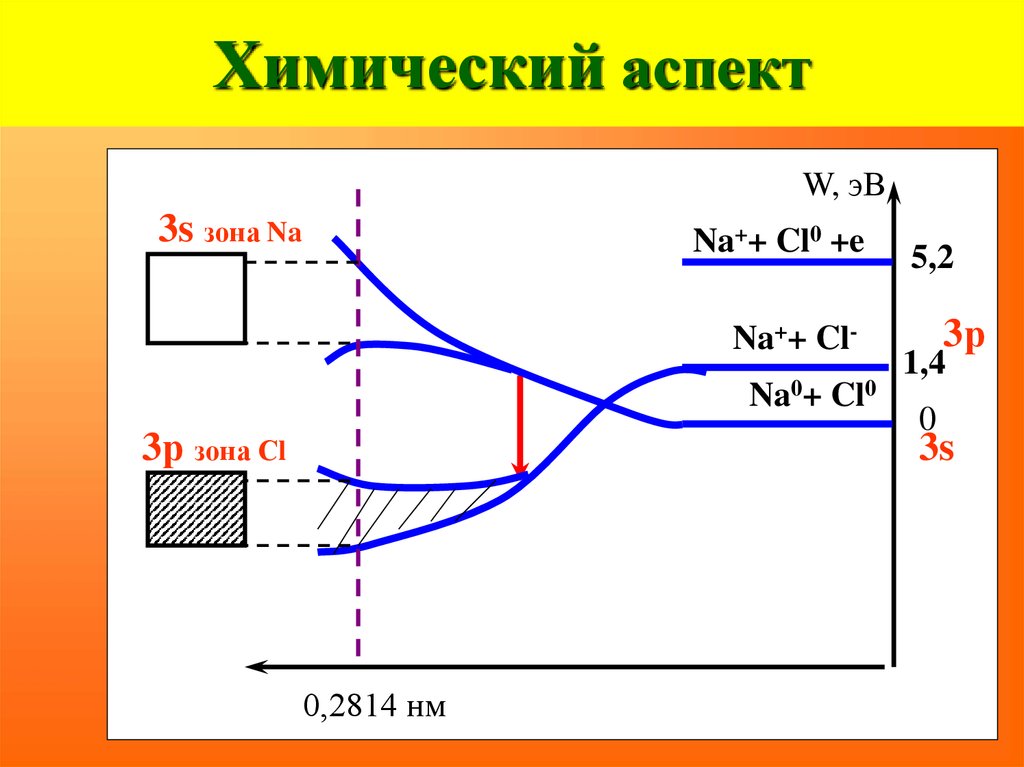
29. Химический аспект
Na : 1s 2 2s 2 2p6 3s 1Cl: 1s 2 2s 2 2p6 3s 2 3p 5
W, эВ
Na++ Cl0 +e
Na++ Cl-
Na0+ Cl0 = 0
Na++ Cl0 +e = 5,2 эВ
Na++ Cl- = 1,4 эВ
Na0+ Cl0
5,2
3р
Cl
1,4
0
3s Na
30. Химический аспект
W, эВ3s зона Na
Na++ Cl0 +e
Na++ ClNa0+ Cl0
3р зона Сl
5,2
3р
1,4
0
3s
0,2814 нм
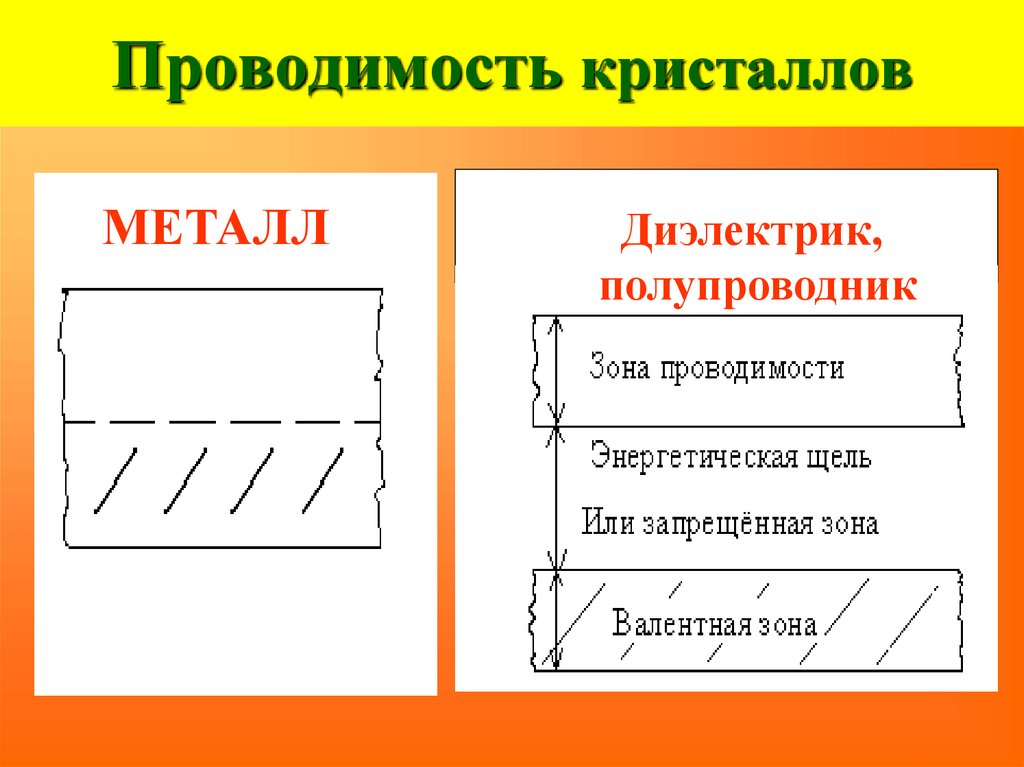
31. Проводимость кристаллов
МЕТАЛЛДиэлектрик,
полупроводник
32. Ширина запрещенной зоны
• Германий Ge• Кремний Si
• Арсенид галлия AsGa
0,7 эВ
1,1 эВ
1,4 эВ
• Сульфид кадмия CdS
• Сульфид цинка ZnS
• Силленит Bi12GeO20
2,4 эВ
3,7 эВ
3,25 эВ
•NaCl
•алмаз
8,6 эВ
5,4 эВ
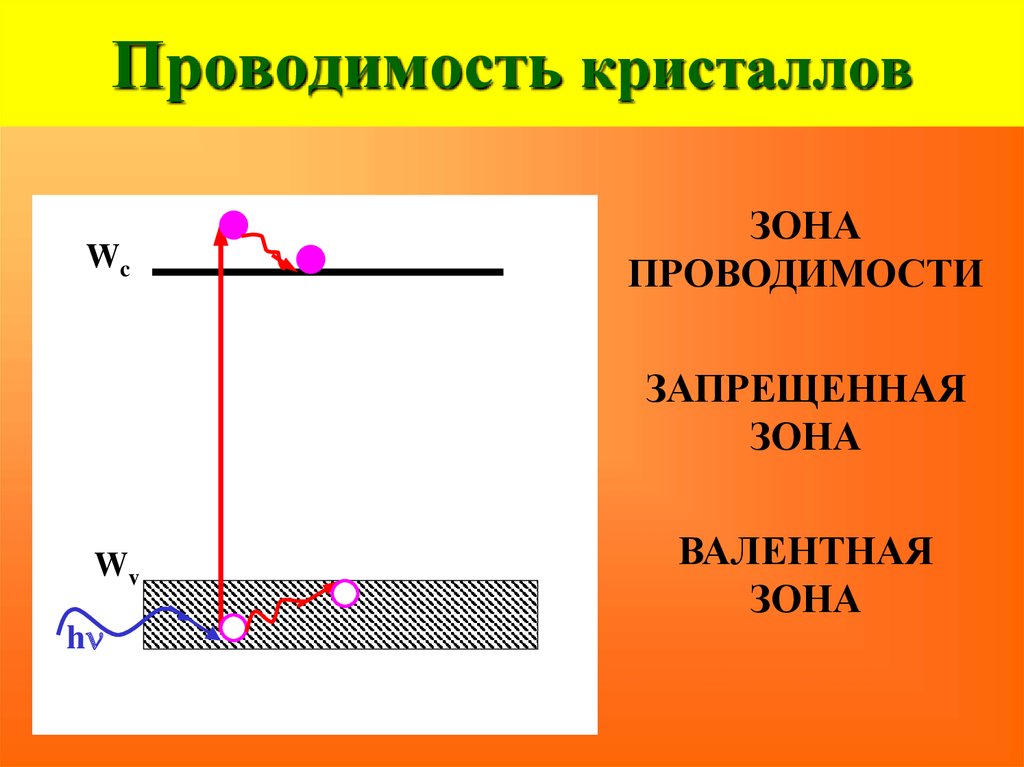
33. Проводимость кристаллов
WcЗОНА
ПРОВОДИМОСТИ
ЗАПРЕЩЕННАЯ
ЗОНА
Wv
hn
ВАЛЕНТНАЯ
ЗОНА
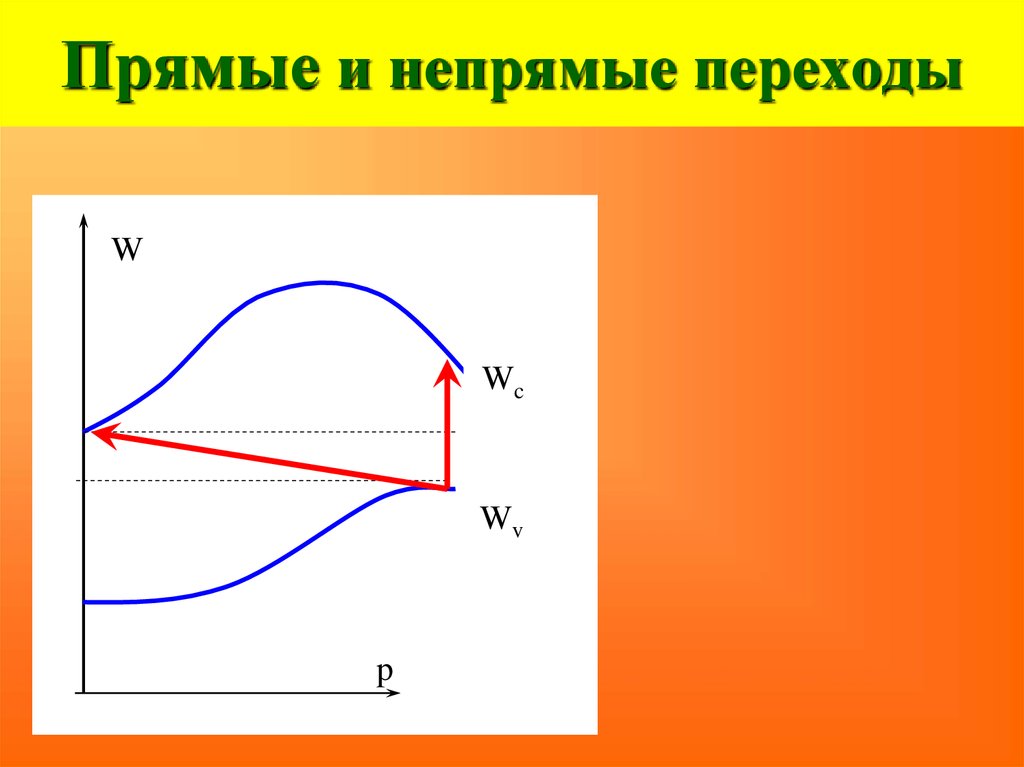
34. Прямые и непрямые переходы
WWc
Wv
p
35. Прямые и непрямые переходы
• Германий Ge• Кремний Si
• Арсенид галлия AsGa
0,7 непрямой
1,1 непрямой
1,4 прямой
• Сульфид кадмия CdS
• Сульфид цинка ZnS
2,4
3,7
• AlxGa1-xAs
x<0,4
x>0,4
• алмаз
прямой
прямой
1,42- 2,16 прямой
непрямой
5,4 непрямой
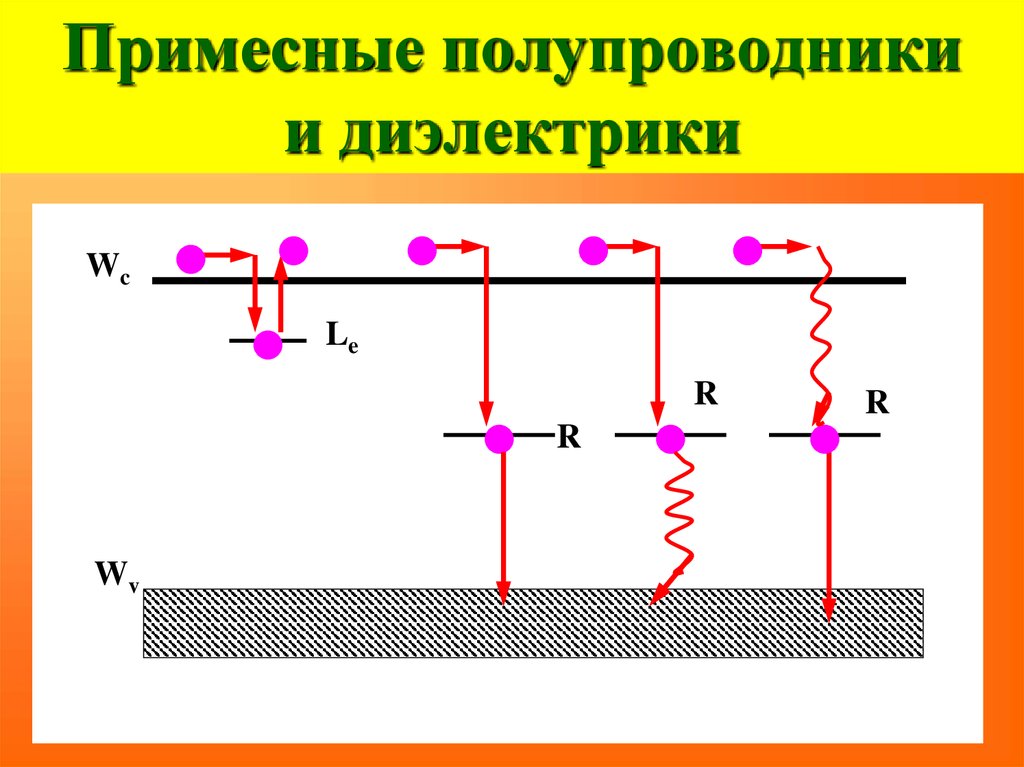
36. Примесные полупроводники и диэлектрики
удельное сопротивление ρ (Ом.см )Чистый Si
5
10
Si c примесью фосфора
1 атом P на 106 атомов Si
2,5
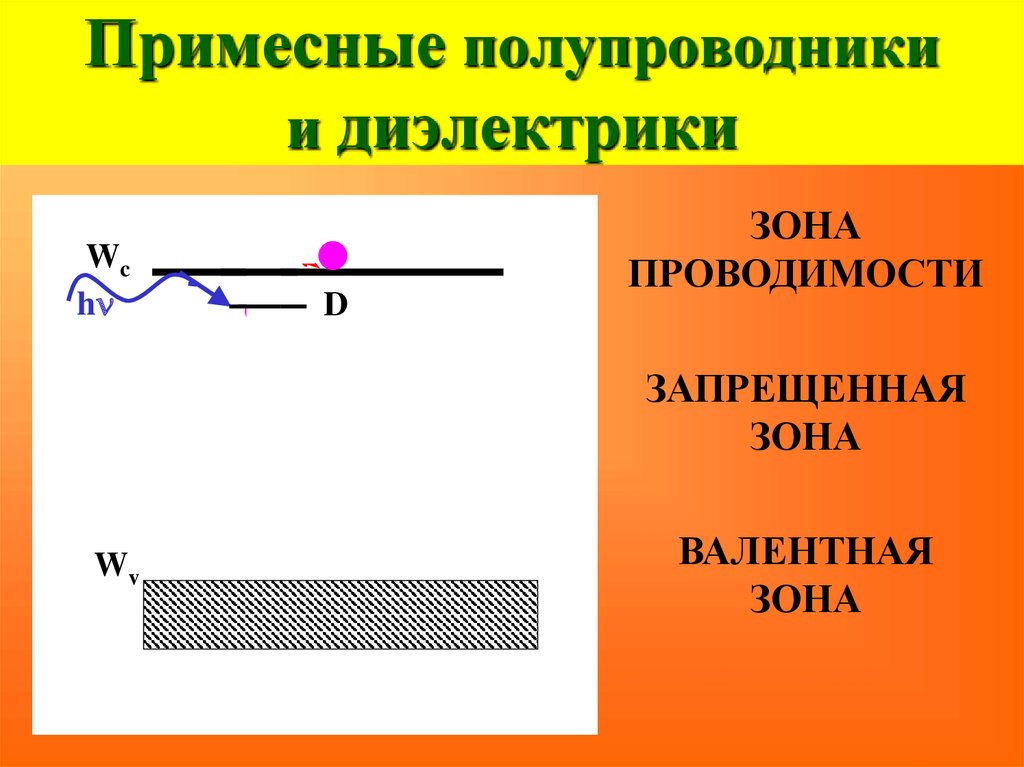
37. Примесные полупроводники и диэлектрики
Wchn
D
ЗОНА
ПРОВОДИМОСТИ
ЗАПРЕЩЕННАЯ
ЗОНА
Wv
ВАЛЕНТНАЯ
ЗОНА
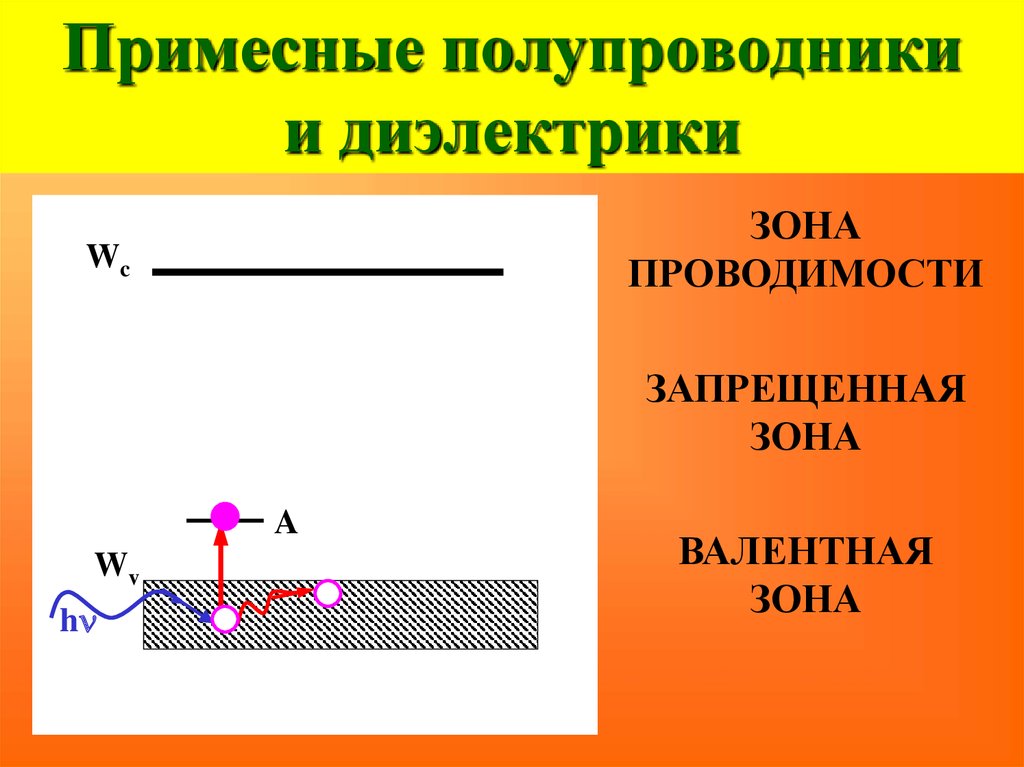
38. Примесные полупроводники и диэлектрики
ЗОНАПРОВОДИМОСТИ
Wc
ЗАПРЕЩЕННАЯ
ЗОНА
A
Wv
hn
ВАЛЕНТНАЯ
ЗОНА
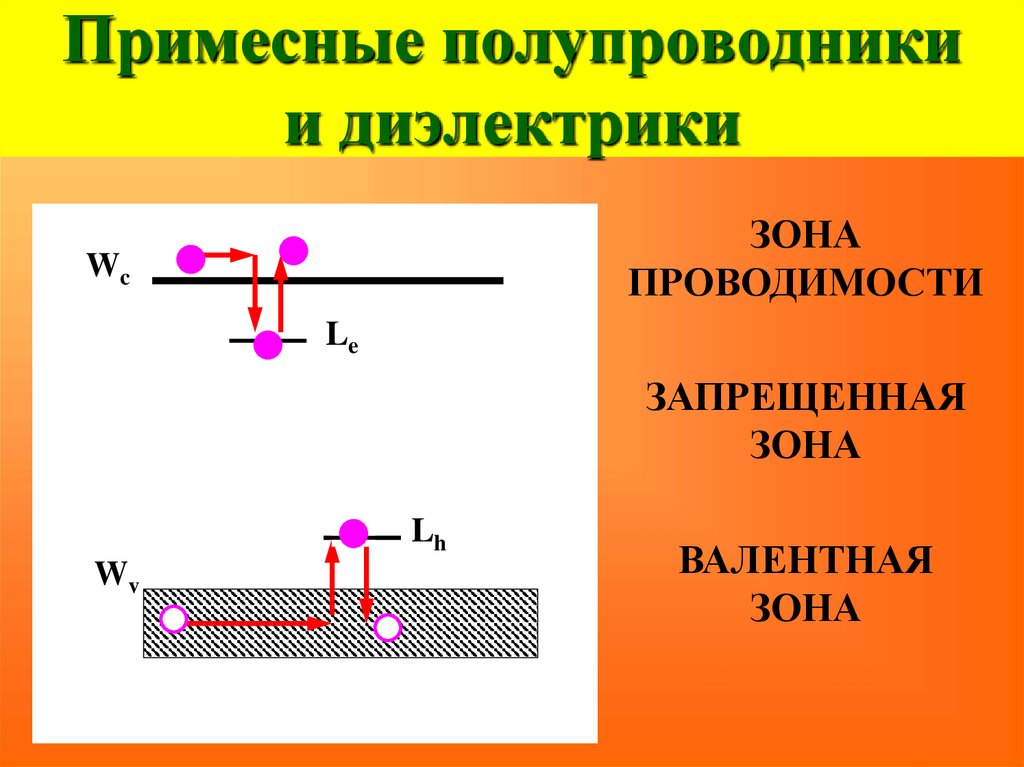
39. Примесные полупроводники и диэлектрики
ЗОНАПРОВОДИМОСТИ
Wc
Le
ЗАПРЕЩЕННАЯ
ЗОНА
Lh
Wv
ВАЛЕНТНАЯ
ЗОНА
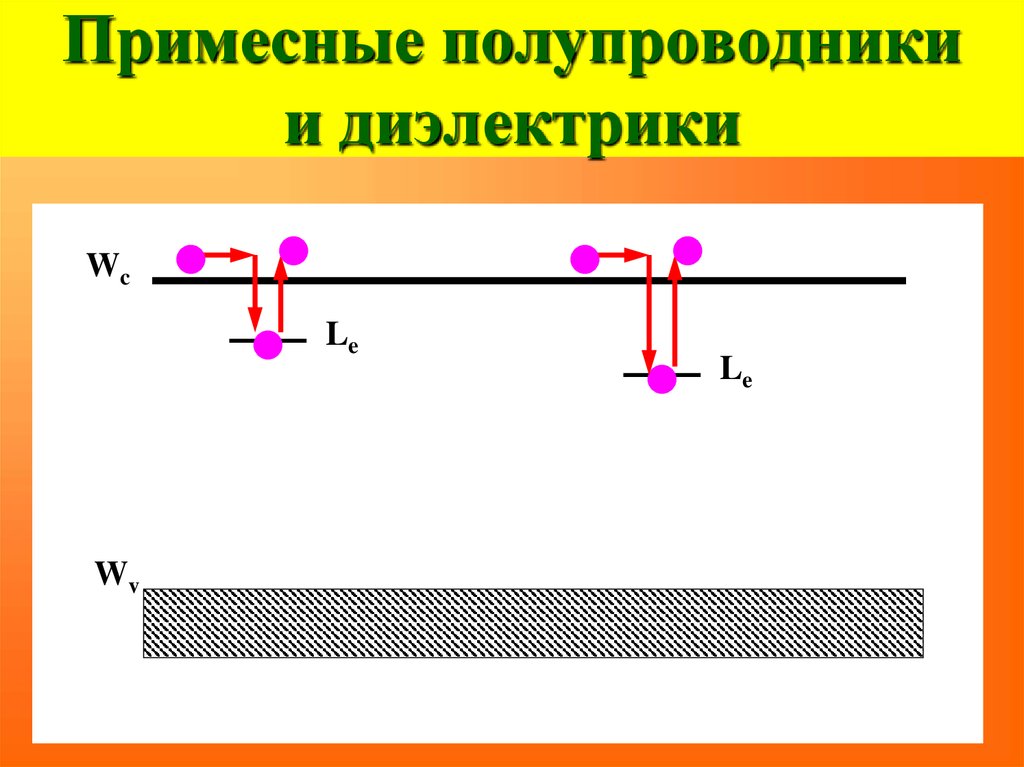
40. Примесные полупроводники и диэлектрики
WcLe
Wv
Le
41. Примесные полупроводники и диэлектрики
WcLe
R
R
Wv
R
42. Подвижность
=V/E- подвижность (см2 · В-1 ·с-1)
V - средняя скорость носителей тока (см· с-1)
E - напряженность электрического поля (В·см-1)
43. Электропроводность
σ = e (μe n + μh p)σ - удельная электропроводность полупроводника
(Ом-1·см-1);
s 1/r
n и p – концентрации электронов и дырок,
e – заряд электрона 1,6·10-19 (Kл) .
44. Статистика равновесных носителей тока
Функции распределения1. Максвелла-Больцмана
f M B Ae
W
где W- заданная энергия,
f - вероятность заполнения частицами
уровня с энергией W,
A- константа,
k- постоянная Больцмана,
T- температура
kT
45. Статистика равновесных носителей тока
Функции распределения2. Ферми-Дирака
1
f F D
e
W WF
kT
1
где W - заданная энергия,
f - вероятность заполнения частицами
уровня с энергией W,
k - постоянная Больцмана,
T - температура,
WF - энергетический параметр
46. Статистика равновесных носителей тока
Функции распределения3. Бозе-Эйнштейна
f B E
e
1
W WB
kT
1
где W - заданная энергия,
f - вероятность заполнения частицами
уровня с энергией W,
k - постоянная Больцмана,
T - температура,
WВ - энергетический параметр
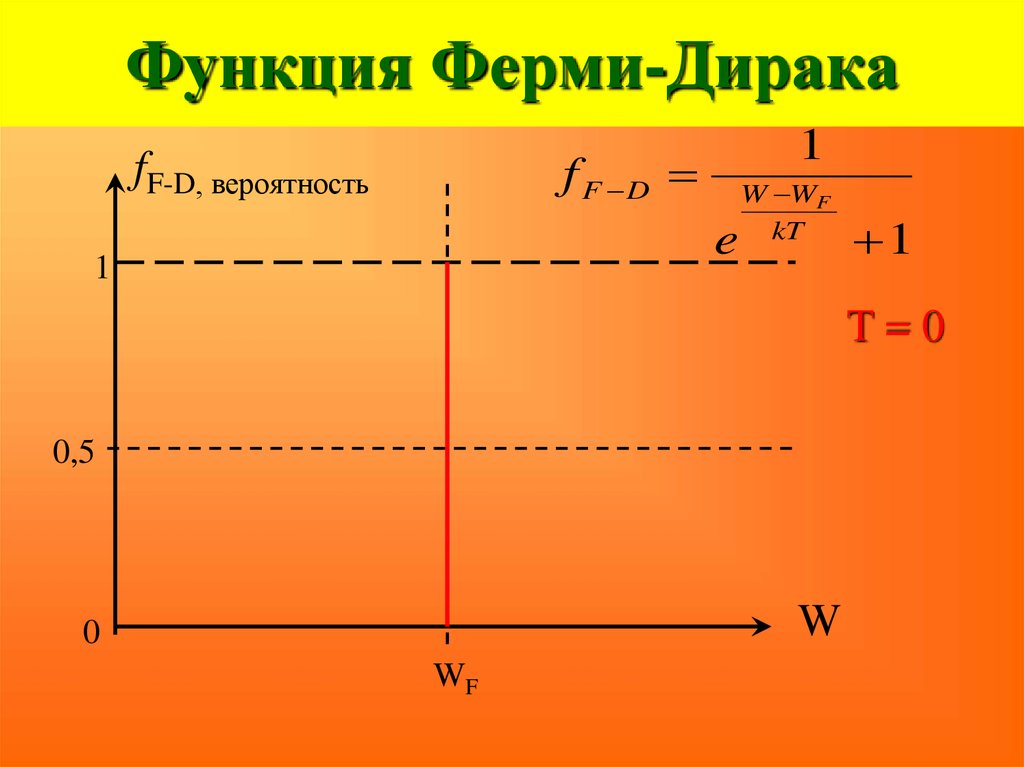
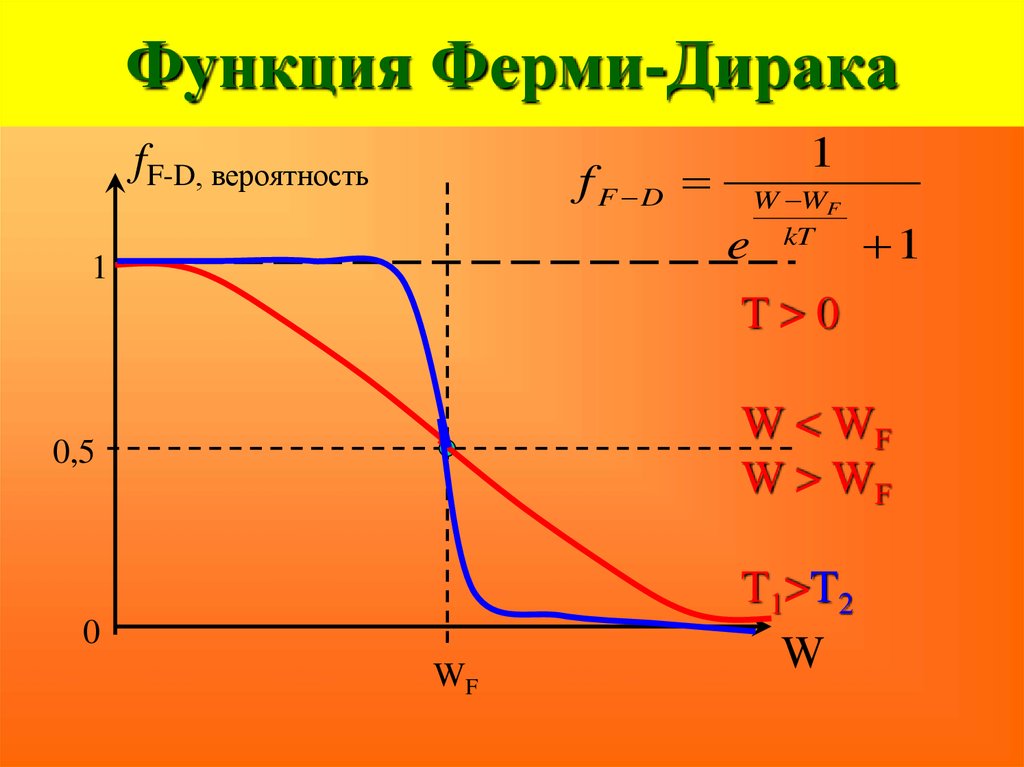
47. Функция Ферми-Дирака
1f F D
fF-D, вероятность
e
1
W WF
kT
1
T=0
0,5
W
0
WF
48. Функция Ферми-Дирака
1f F D
fF-D, вероятность
e
1
W WF
kT
1
T>0
W = WF
0,5
W
0
WF
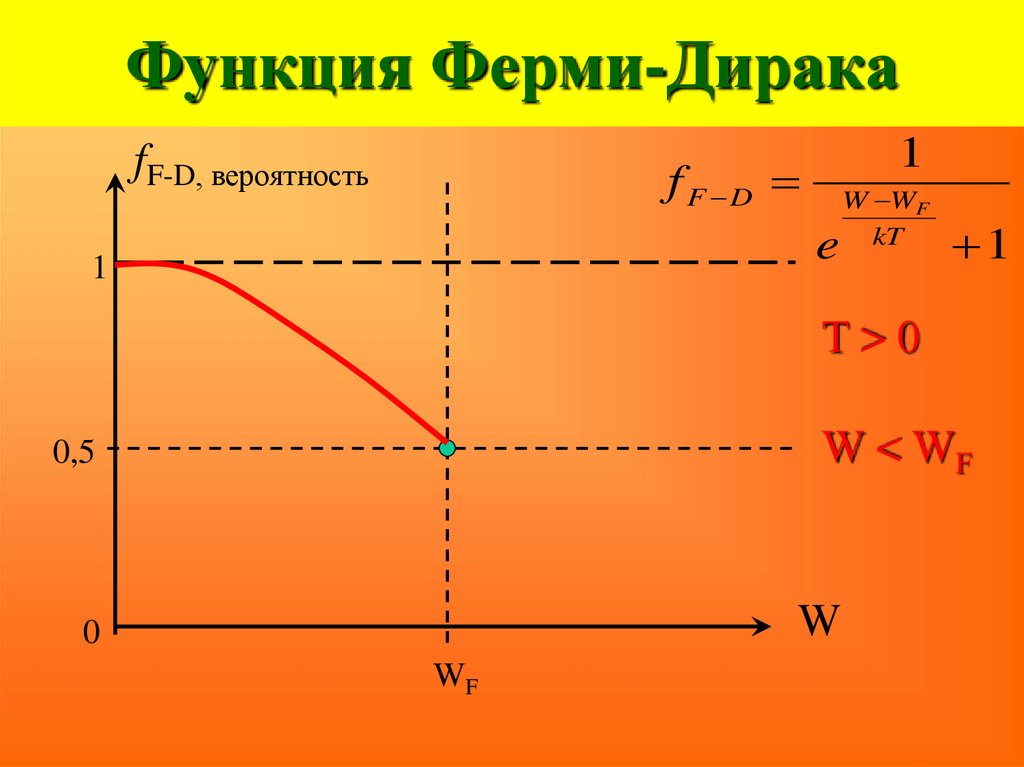
49. Функция Ферми-Дирака
fF-D, вероятность1
f F D
e
1
W WF
kT
1
T>0
W < WF
0,5
W
0
WF
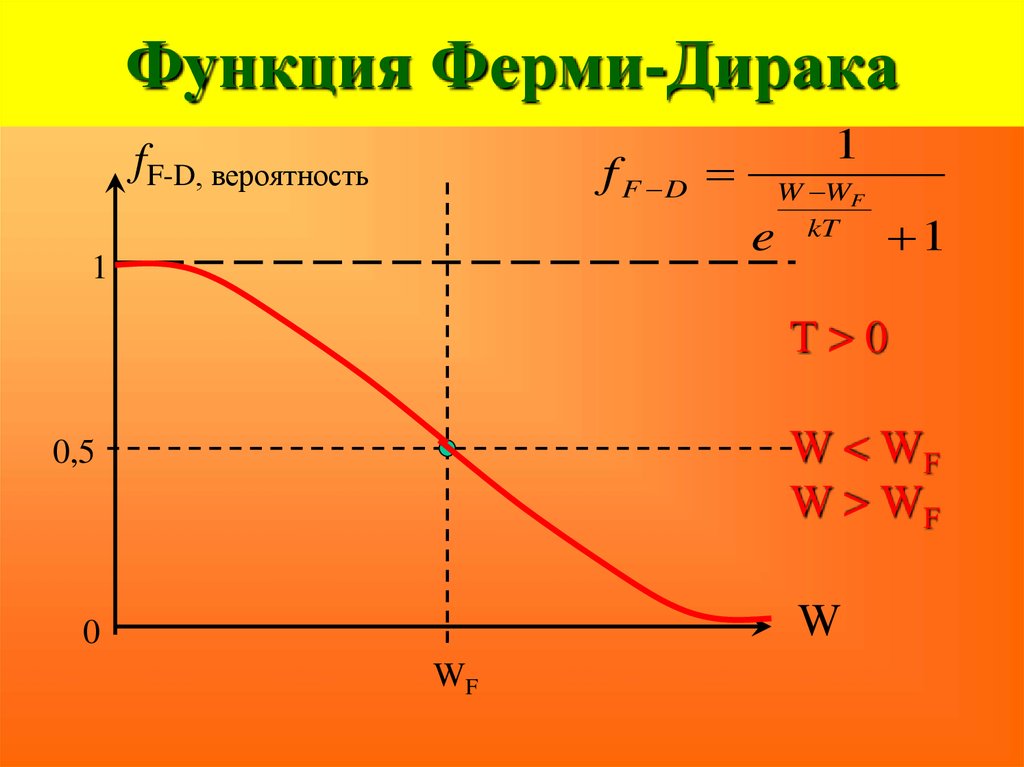
50. Функция Ферми-Дирака
1f F D
fF-D, вероятность
e
1
W WF
kT
1
T>0
W < WF
W > WF
0,5
W
0
WF
51. Функция Ферми-Дирака
fF-D, вероятность1
f F D
e
1
W WF
kT
1
T>0
W < WF
W > WF
0,5
0
WF
T1>T2
W
52. Функция Ферми-Дирака
|W| >> |WF|1
fF D
e
W WF
kT
e
W WF
kT
WF
e
kT
e
W
kT
1
f F D Ae
W
kT
W WF 2kT
53. Некоторые полезные величины
kT = 0,026 эВпри Т=300 К
Значения постоянной Больцмана
1,38 10-23 Дж/К
8,62 10−5 эВ/К
54. Функция Ферми-Дирака
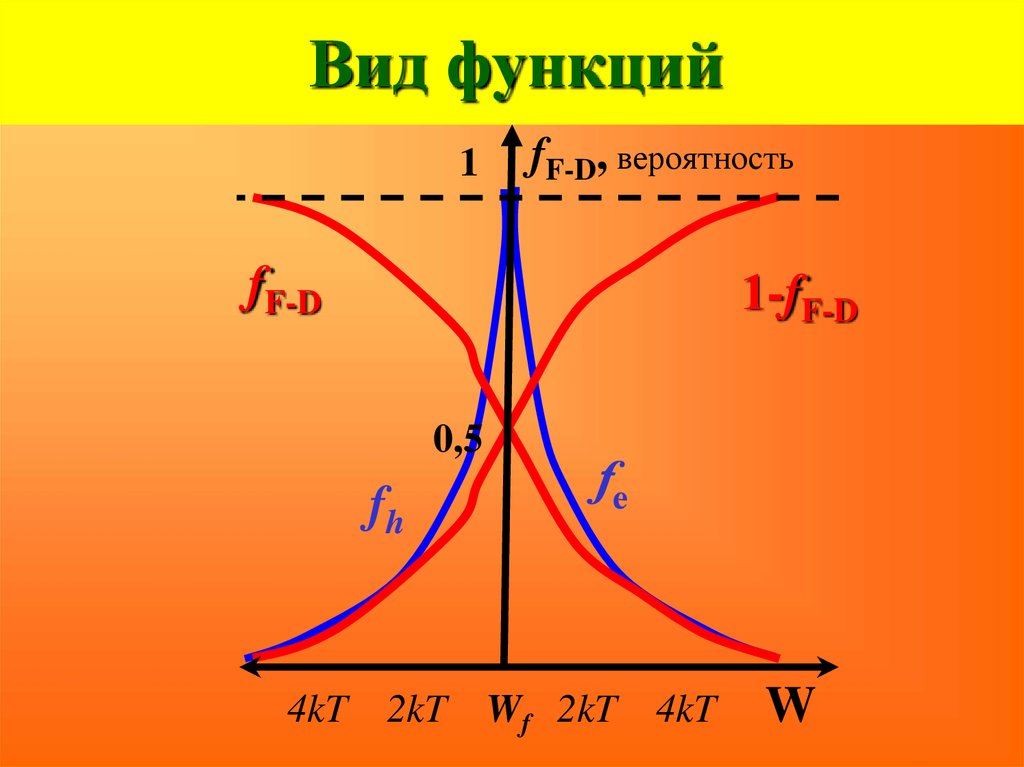
W > WFfe e
(W WF )
kT
55. Функция Ферми-Дирака
W < WFfh e
W WF
kT
56. Вид функций
1fF-D, вероятность
fF-D
1-fF-D
0,5
fh
4kT 2kT Wf 2kT 4kT
W
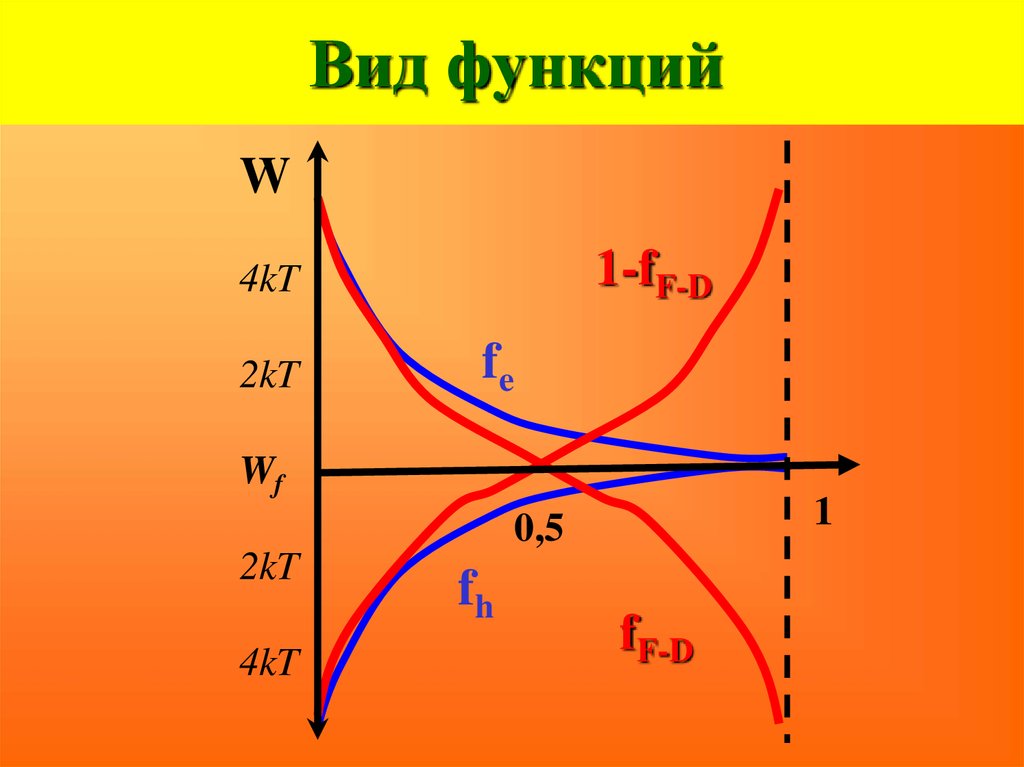
57. Вид функций
W1-fF-D
4kT
2kT
fe
Wf
1
0,5
2kT
4kT
fh
fF-D
58. Расчет концентраций носителей тока в собственном полупроводнике
Пусть в кристалле единичного объема в интервалеэнергий от W до W+dW имеется dZ квантовых
состояний.
dZ
NW
dW
вероятность заполнения состояния с энергией W
дается функцией f F D , концентрация
электронов в этих состояниях равна:
dn f F D dZ f F D NW dW
59. Расчет концентраций носителей тока в собственном полупроводнике
W2n
f F D N W dW
W1
NW C
2m
4 2
h
*
e
3/ 2
(W WC )
1/ 2
NWC – функция плотности состояний
m* - эффективная масса электронов в зоне проводимости,
h - постоянная Планка,
WС - энергия дна зоны проводимости.
60. Расчет концентраций носителей тока в собственном полупроводнике
NW C2m
4 2
h
NW V
2m
4 2
h
*
e
*
h
3/ 2
(W WC )
1/ 2
Wc
3/ 2
(WV W )
1/ 2
Wv
m*e- эффективная масса электронов в зоне проводимости,
m*h- эффективная масса дырок в валентной зоне,
h - постоянная Планка,
WC - энергия дна зоны проводимости
WV - энергия потолка валентной зоны
61. Расчет концентраций носителей тока в собственном полупроводнике
W2n
n
f
W1
F D
NC
N W dW
f (W
e
)
C
NC - эффективная плотность состояний
fe(WC) - значение функций распределения
для энергии W=WC.
Wc
Wv
62. Расчет концентраций носителей тока в собственном полупроводнике
fN C f e (WC )
F D
N W dW
WC
При условии
NC e
W W
C F
kT
WC WF 2kT.
4 e
WC
W WF
kT
* 3/ 2
e
2m
2
h
1/ 2
(W WC ) dW
63. Расчет концентраций носителей тока в собственном полупроводнике
NC eW WF
C
kT
4 e
W WF
kT
WC
2m
N C 4 2
h
*
e
3/ 2
e
2m
2
h
*
e
W WC
kT
3/ 2
(W WC )1/ 2 dW
(W WC )
WC
Интегрируем по частям, как произведение
U (W WC ) / kT
1/ 2
dW
64. Расчет концентраций носителей тока в собственном полупроводнике
2m kTN C 4
2
h
*
e
3/ 2
U
1/ 2
e
U
dU
WC
2m kT
4
2
h
*
e
NC
2 m kT
2
h
*
e
2
3/ 2
3/ 2
2
65. Расчет концентраций носителей тока в собственном полупроводнике
2 m kTN C 2
h
*
e
2
3/ 2
2 mh* kT
NV 2
2
h
3/ 2
15 m
5 10
m
*
e
3
2 32
T
3
*
2
3
m
15
h
5 10 T 2
m
66. Расчет концентраций носителей тока в собственном полупроводнике
2 m kTn N C f e (WC ) 2
h
*
e
2
2 m kT
p NV f h (WV ) 2
h
*
h
2
3/ 2
e
3/ 2
e
WC WF
kT
(WV WF )
kT
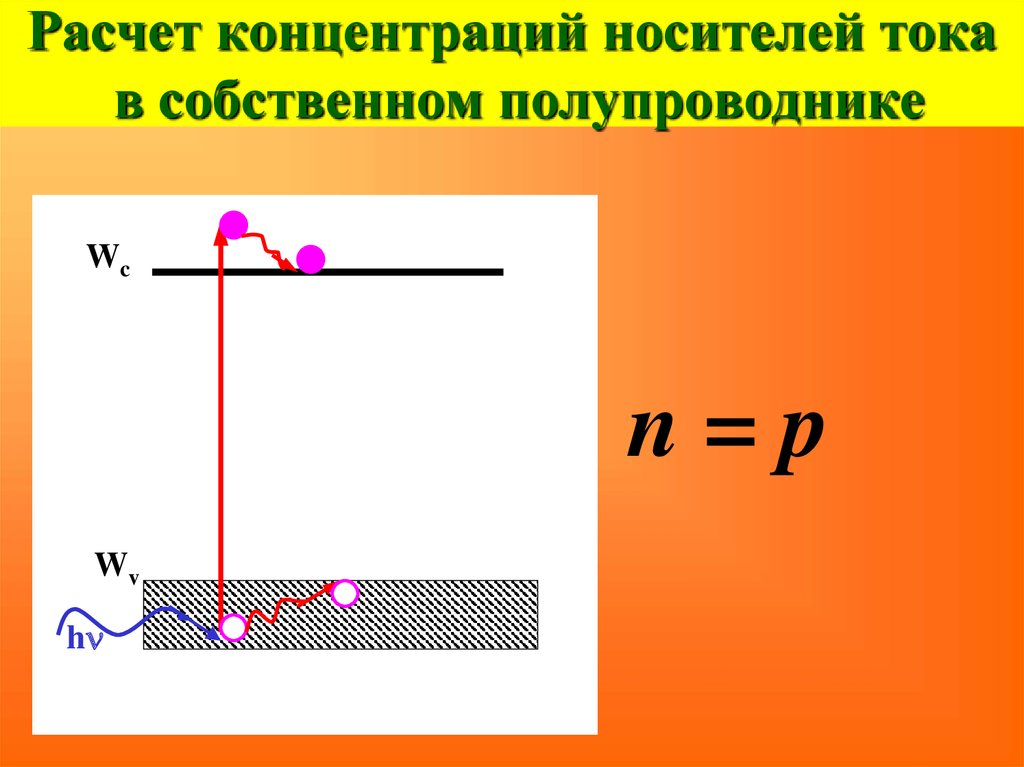
67. Расчет концентраций носителей тока в собственном полупроводнике
Wcn=p
Wv
hn
68. Расчет концентраций носителей тока в собственном полупроводнике
В собственном полупроводнике n = p2 m kT
2
h
*
e
2
m
* 3/ 2
e
e
3/ 2
e
W WF
C
kT
WC WF
kT
2 m kT
2
h
*
h
2
* 3/ 2
h
m
e
3/ 2
e
WV WF
kT
WV WF
kT
;
69. Расчет концентраций носителей тока в собственном полупроводнике
m* 3/ 2
e
e
WC WF
kT
* 3/ 2
h
m
e
WV WF
kT
WC WF WV WF 3 m
ln
kT
2 m
*
h
*
e
70. Расчет концентраций носителей тока в собственном полупроводнике
WC WF WV WF 3 mln
kT
2 m
*
h
*
e
m
3
2WF WC WV kT ln
2
m
*
h
*
e
71. Расчет концентраций носителей тока в собственном полупроводнике
WC WV 3kT mWF
ln
2
4
m
*
h
*
e
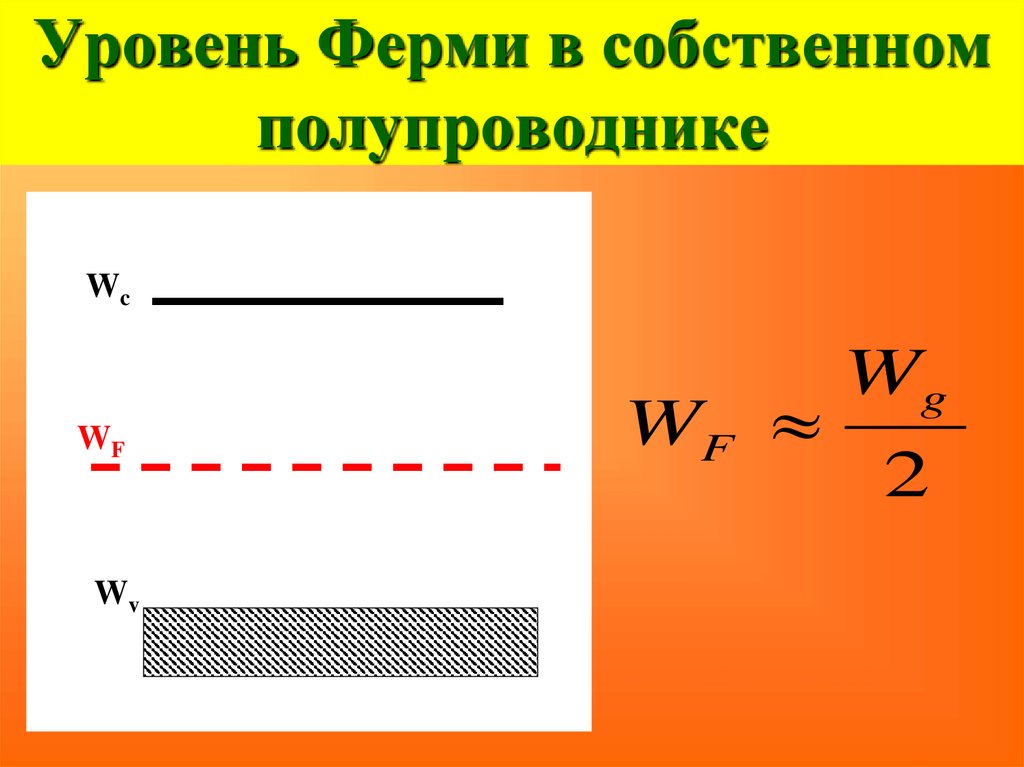
72. Уровень Ферми в собственном полупроводнике
WcWF
Wv
WF
Wg
2
73. Соотношение носителей тока
n n p Nc Nv e2
i
W f
Nc Nve
Wc Wv
kT
Wc WF Wv WF
kT
Nc Nve
Wg
kT
N
74. Соотношение носителей тока
ni n p N c N v eni B T
3
2
e
Wg
2 kT
Wg
2 kT
B, K-3/2 см-3
Wg, эВ
Si
3,84 1016
1,21
Ge
1,76 1016
0,785
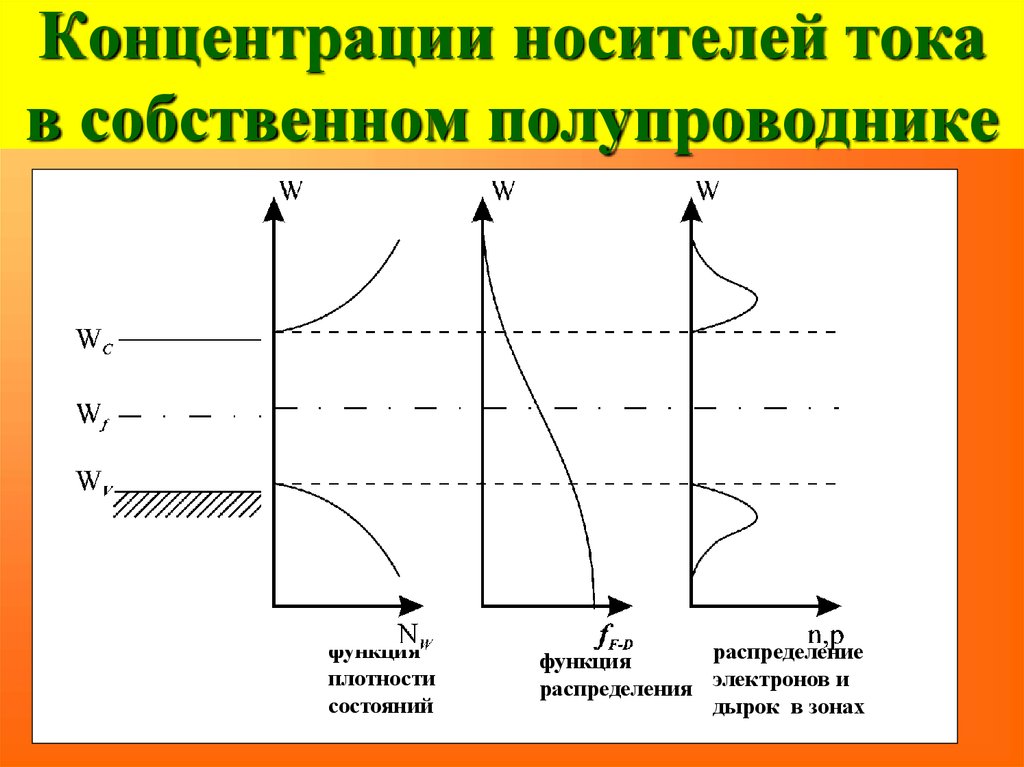
75. Концентрации носителей тока в собственном полупроводнике
функцияплотности
состояний
распределение
функция
распределения электронов и
дырок в зонах
76. ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
77. Расчет концентраций носителей тока в примесном полупроводнике
ndNd
1
e
Wd WF
kT
;
1
nd - концентрация электронов на донорах,
Nd – концентрация доноров,
Wd - энергии донорных (отсчитанные от потока валентной зоны),
- фактор спинового вырождения (от 1 до 2, если доноры могут
отдавать кристаллу, а акцепторы принимать от кристалла только по
одному электрону; тогда =2).
78. Расчет концентраций носителей тока в примесном полупроводнике
Ndpd
e
WF Wd
kT
;
1
pd - концентрация дырок на донорах,
Nd – концентрация доноров,
Wd - энергии донорных (отсчитанные от потока валентной зоны),
- фактор спинового вырождения.
79. Расчет концентраций носителей тока в примесном полупроводнике
paNa
1
e
WF Wa
kT
;
1
ра- концентрация дырок на акцепторах,
Nа – концентрация акцепторов,
Wа - энергии акцепторных уровней (отсчитанные от потока
валентной зоны),
- фактор спинового вырождения
80. Расчет концентраций носителей тока в примесном полупроводнике
Nana
e
Wa WF
kT
,
1
nа - концентрация электронов на акцепторах,
Nа – концентрация акцепторов,
Wа - энергии акцепторных уровней (отсчитанные от потока
валентной зоны),
- фактор спинового вырождения
81. Допущения
1. Уровень Ферми не приближается крассматриваемым уровням ближе, чем на 2kT
2. Электрическая нейтральность полупроводника
n nd p pa N d N a
82. Расчет
Чисто примесная проводимость на примерепроводника n-типа
При низких температурах электроны в зону
проводимости поставляют доноры, а генерация
из валентной зоны пренебрежимо мала.
=> Na, p, pa равны нулю
n N d nd = pd
83.
NC eWC W F
kT
1
Nd e
2
W F Wd
kT
Wd WC kT
Nd
WF
ln(
)
2
2
2NC
84.
При Т=0 и при Nd=2Nc уровень Ферми лежит точнопосредине между уровнями доноров и дном зоны
проводимости.
Wc
WF
Wv
В реальных условиях (Т > 0 K, Nd > 2Nc ) он
немного сдвинут вверх.
85.
Компенсированныйполупроводник
Nd Na
n nd p pa N d N a
n nd p pa 0N d
86.
nd 0Wc
WF
Wv
pa 0
n=p
87. Частично компенсированный полупроводник
Примем, что Nd = 2 Napα и p равны нулю. При низкой температуре
степень ионизации доноров мала => n = 0
nd N d N a
nd N d f
88.
Nd Naf
Nd
f 2e
Nd Na
2e
Nd
Wd WF
kT
Wd W F
kT
89.
2Na Na 12e
2Na
2
Wd WF
kT
WF Wd 1,38kT
90.
WF Wd 1,38kTПри Т=0,
WF Wd 1,38kT
91. Положение уровня Ферми
WWC
WD
Wg/2
WA
WV
0
0,01 0,1
0,5 1
2
10 100
NA
ND
92. Температурная зависимость
WWс
s
WС + WD
2
WD
кТ
Wс
2
Т
Т
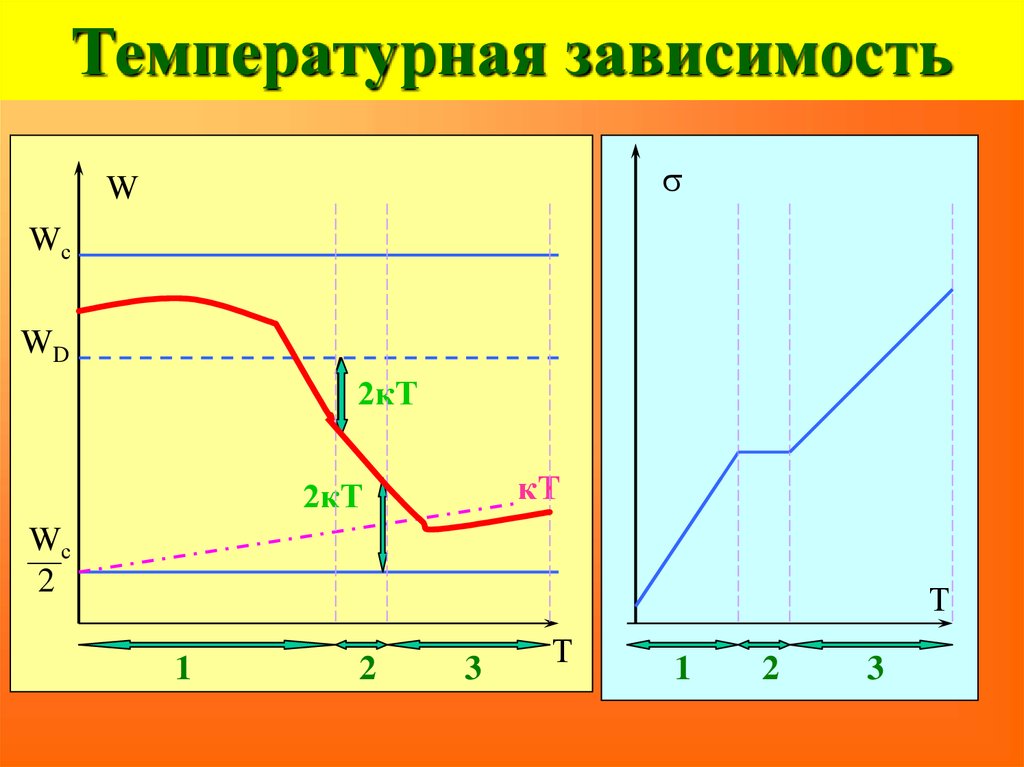
93. Температурная зависимость
sW
Wс
WD
2кТ
кТ
Wс
2
Т
1
Т
1
94. Температурная зависимость
Температура истощения примеси ТsT
T
D
S
А
S
WC W D
2NC
k ln(
)
ND
W А WV
2 NV
k ln(
)
NA
95. Температурная зависимость
sW
Wс
WD
2кТ
2кТ
кТ
Wс
2
Т
1
2
Т
1
2
96. Температурная зависимость
Температура ионизации Тi (переход ксобственной проводимости)
T
i
k ln(
Wg
NV N C
N
2
)
N – концентрация примеси
Для Ge, легированного донорной примесью
ND = 1022 м-3 и WD=0,01эВ
Ts = 32 K, Ti = 450 K
97. Температурная зависимость
Температурная зависимостьs
W
Wс
WD
2кТ
кТ
2кТ
Wс
2
Т
1
2
3
Т
1
2
3
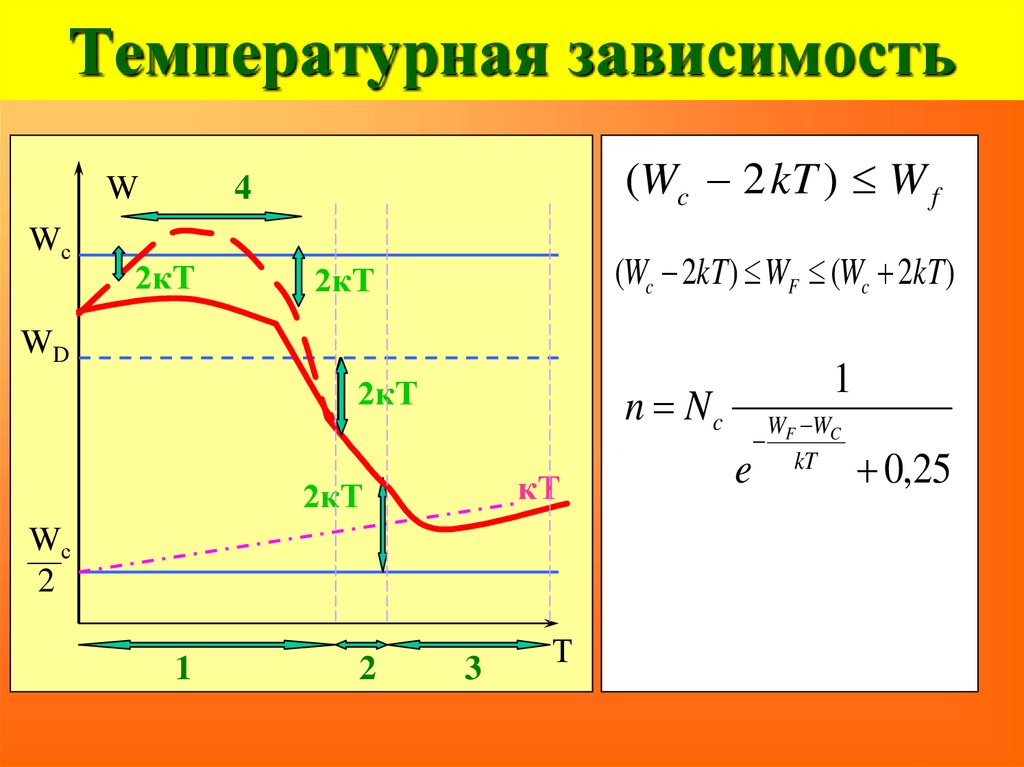
98. Температурная зависимость
WWс
(Wc 2 kT ) W f (W
4
2кТ
(Wc 2kT ) WF (Wc 2kT )
2кТ
WD
2кТ
n Nc
кТ
2кТ
Wс
2
1
2
1
3
Т
e
WF WC
kT
0,25
99. Температурная зависимость
WWс
4
2кТ
2кТ
WD
2кТ
кТ
2кТ
Wс
2
1
2
3
Т




















































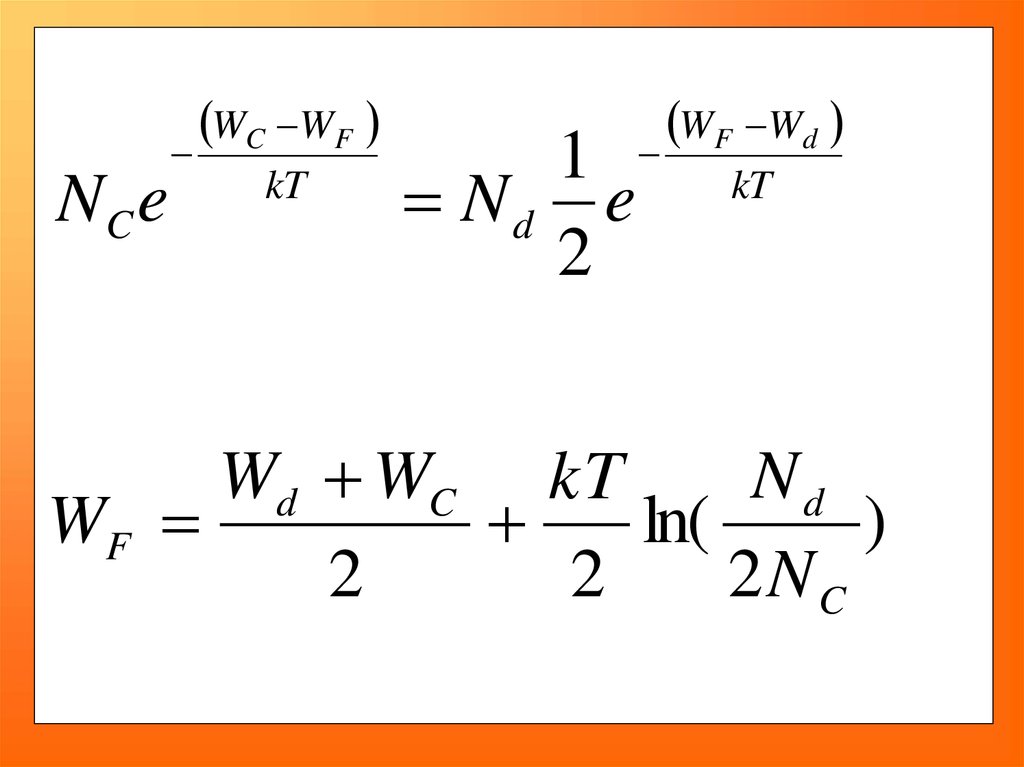





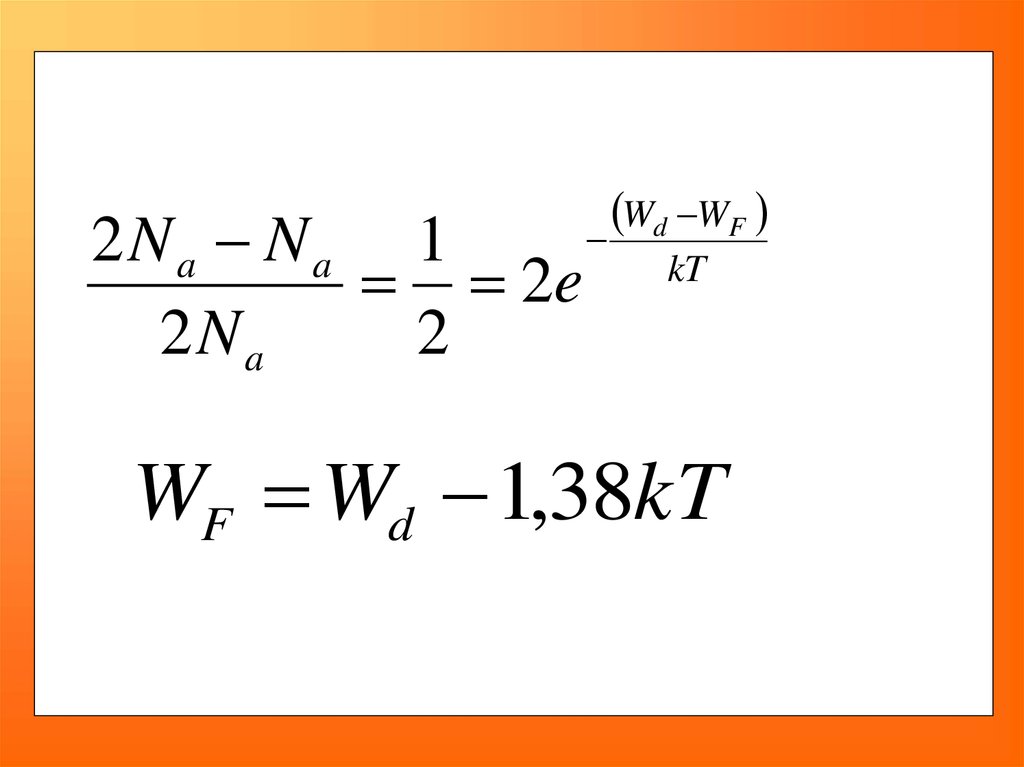



 physics
physics electronics
electronics








