Типы твердых тел. Зонная картина

1. Типы твердых тел. Зонная картина.

Выполнила: Нигматуллина Э.Р.
Гр. 4 Ф-2

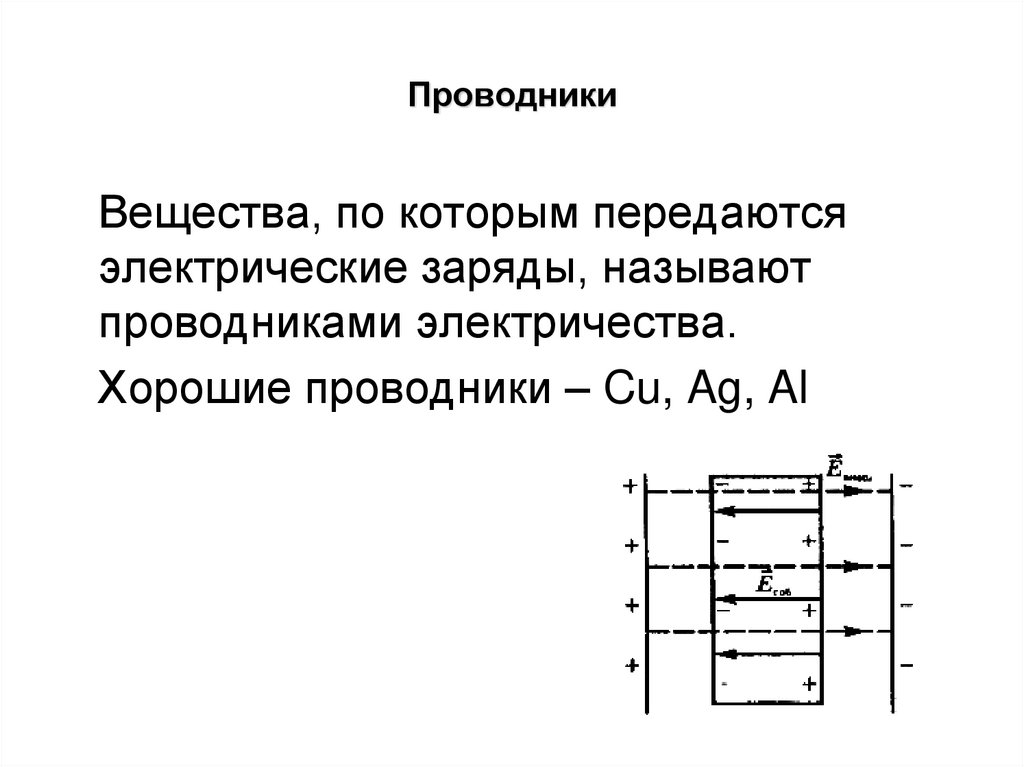
2. Проводники

Вещества, по которым передаются
электрические заряды, называют
проводниками электричества.
Хорошие проводники – Cu, Ag, Al

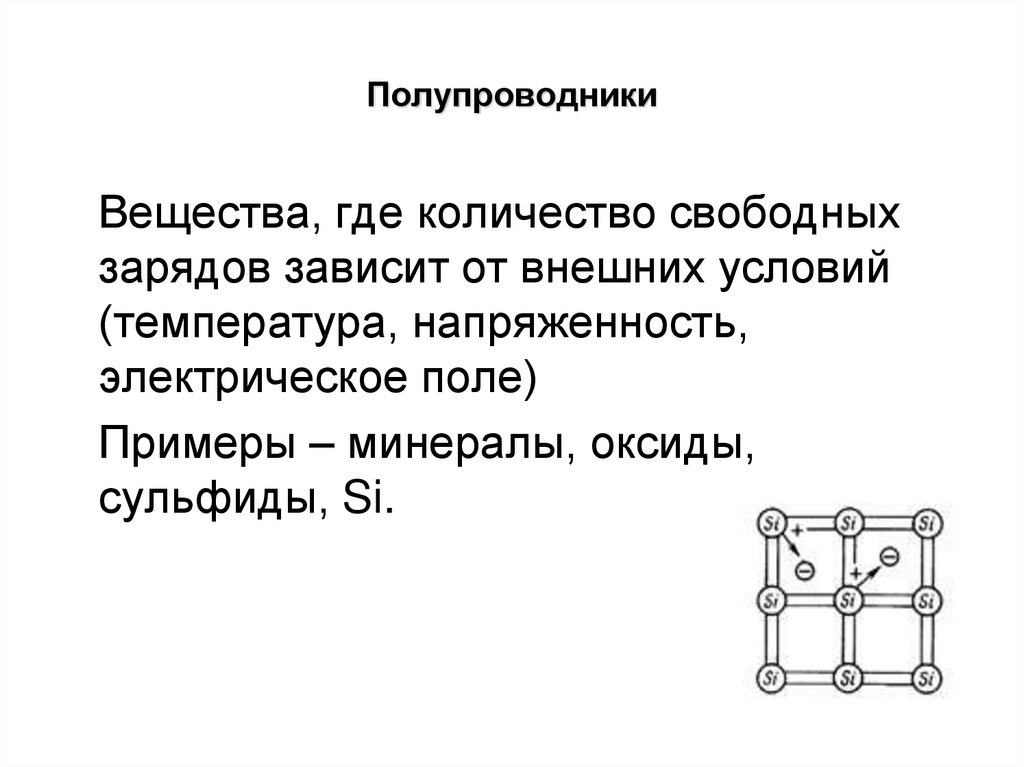
3. Полупроводники

Вещества, где количество свободных
зарядов зависит от внешних условий
(температура, напряженность,
электрическое поле)
Примеры – минералы, оксиды,
сульфиды, Si.

4. Изоляторы

Материалы, внутренние электрические
заряды которых не текут свободно, и
при этом возникают трудности при
проведении электрического тока под
влиянием электрического поля.
Примеры – стекло , бумага , резина,
полимеры.

5. Постулаты зонной теории

• Приближение Борна- Оппенгеймера;
• Приближение периодического
U(r) U(r a n )
потенциала:
• Одноэлектронное приближение (Метод
Хартри- Фока):
U U яд U эл эл U ядер U эфф.пол

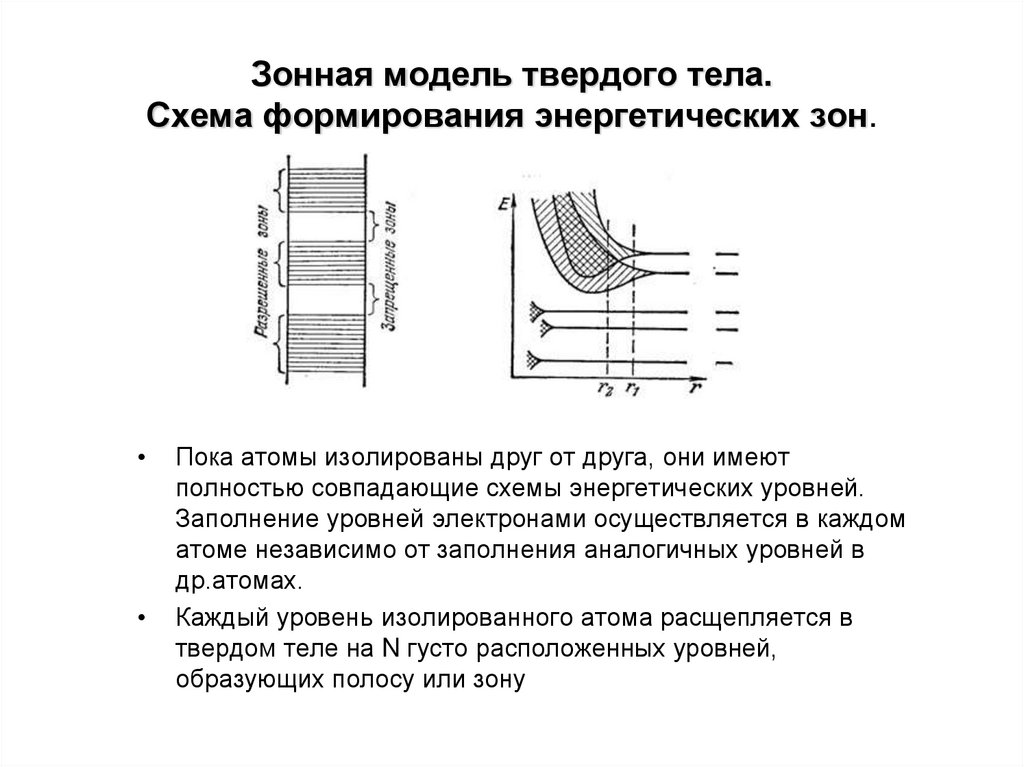
6. Зонная модель твердого тела. Схема формирования энергетических зон.

Пока атомы изолированы друг от друга, они имеют
полностью совпадающие схемы энергетических уровней.
Заполнение уровней электронами осуществляется в каждом
атоме независимо от заполнения аналогичных уровней в
др.атомах.
Каждый уровень изолированного атома расщепляется в
твердом теле на N густо расположенных уровней,
образующих полосу или зону

7. Уравнение Шредингера  для кристаллов

Уравнение Шредингера
для кристаллов
Где m,M – массы электронов и ядер
Z j , Zn
атомные номера ядер
R jn , rik , rij расстояния между ядрами и электронами
E –
полная энергия кристалла
волновая функция системы атомов и
электронов

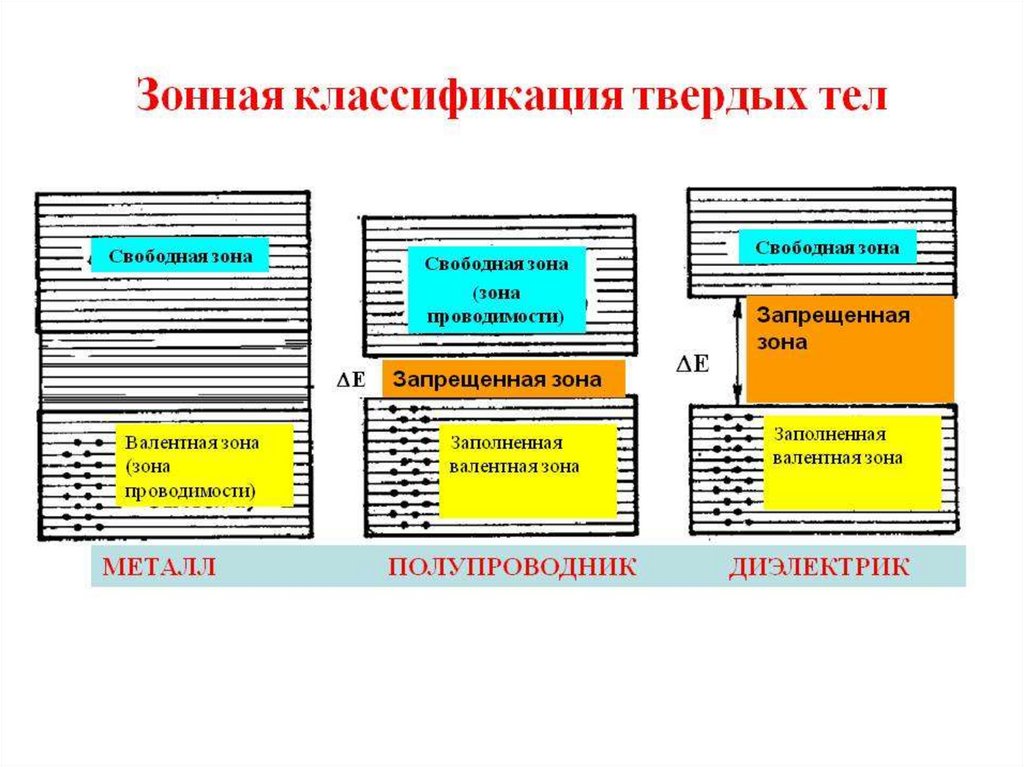
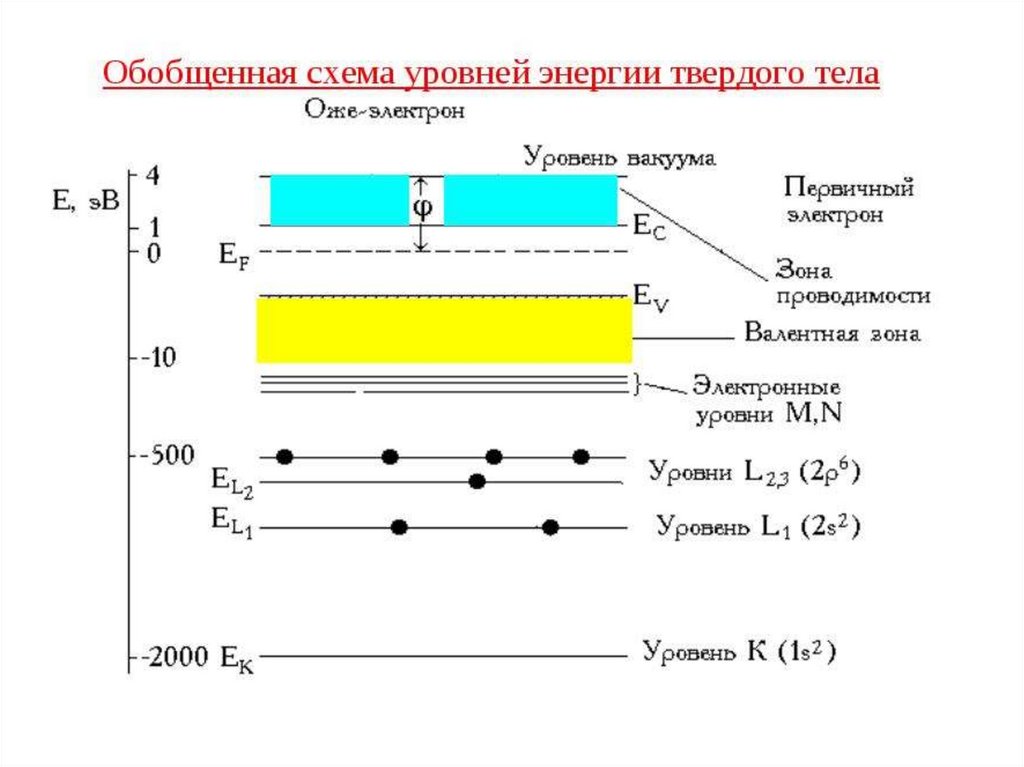
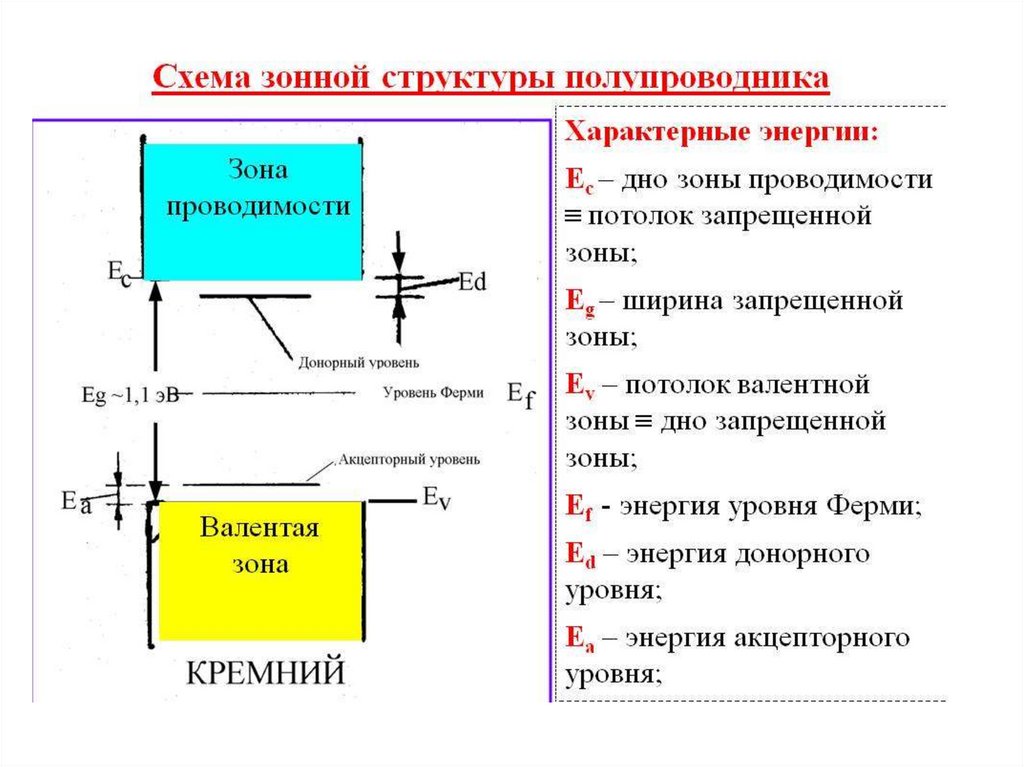
8. Зонная классификация твердых тел.

9.

10.

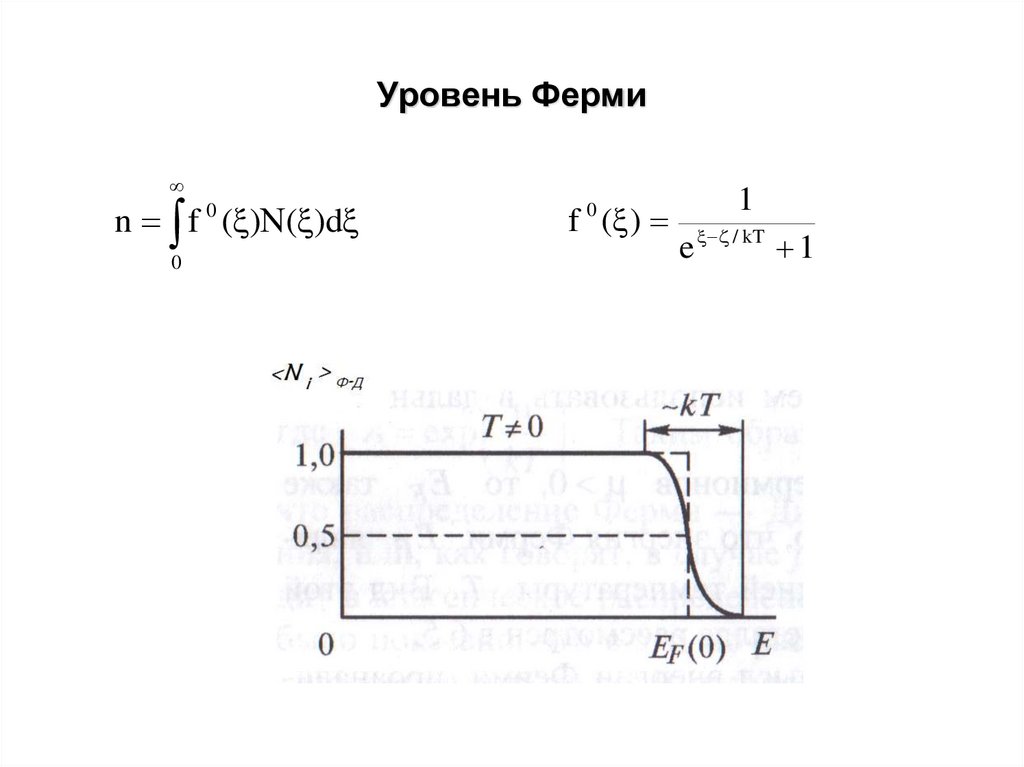
11. Уровень Ферми

n f 0 ( ) ( )d
0
f 0 ( )
1
e / kT 1

12. Распределение Ферми - Дирака

k (E) k ' (E )
Pkk' f (E)([1 f [E )]]p( )
Pk 'k f (E )[1 f (E)]p(0)
В равновесном состоянии :
f (E)[1 f (E )]p( ) f (E )[1 f (E)]p(0)
=
f (E ) 1 f (E) p( )
e / kT
1 f (E ) f (E)
p(0)
При любых T
1 f (E)
e ( E ) / kT
f (E)
f (E )
e [( E ) ] / kT
1 f (E )
Если решим уравнение относительно f(E), то получим функцию Ферми - Дирака

13.

f (E)
1
e
Где µ - химический потенциал
( E ) / kT
1

14. Литература

• Д. Займан «Принципы теории твердого
тела»
• А.С. Давыдов «Теория твердого тела»