Similar presentations:
Элементы зонной теории твердого тела
1. Лекция 3: Элементы зонной теории твердого тела
Разрешённые и запрещённые по энергии зоны вкристаллах.
•Расщепление атомных уровней в зоны.
•Металлы, диэлектрики и полупроводники с точки зрения зонной
теории.
•Уравнение Шредингера для кристалла - адиабатическое
приближение, одноэлектронное приближение, электрон в
периодическом потенциале, Блоховские волны.
•Квазиимпульс, модель расширенных и приведённых зон Бриллюэна.
•Электрон в твердом теле как квазичастица.
2. Таблица Менделеева
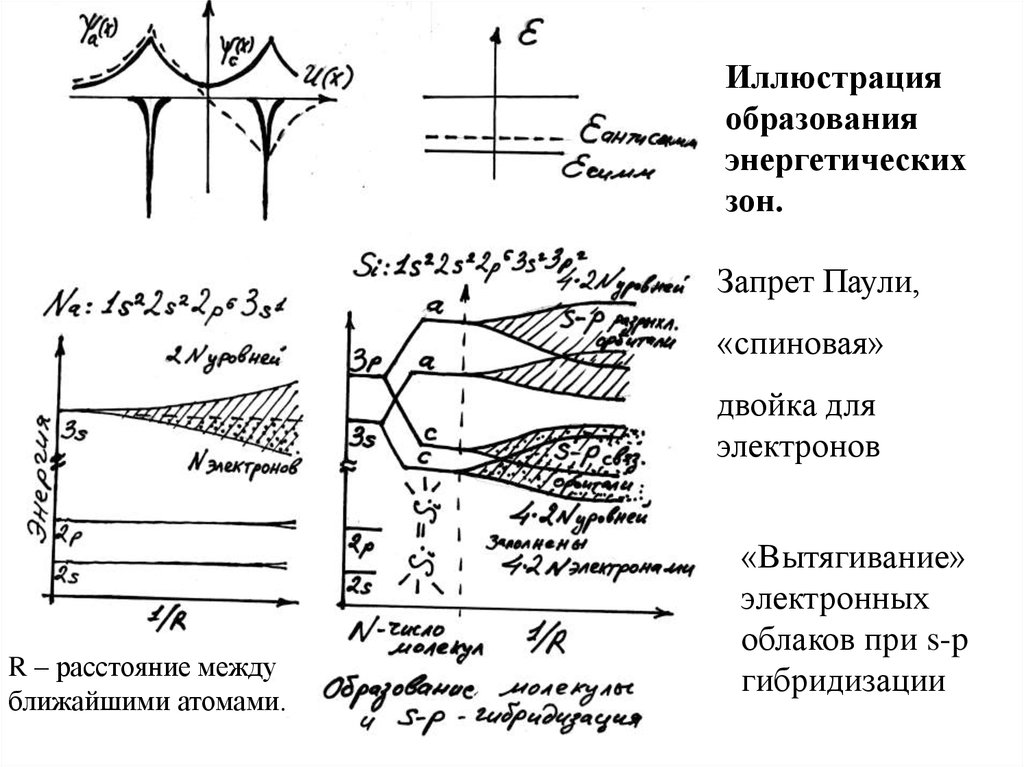
3. Иллюстрация образования энергетических зон.
Запрет Паули,«спиновая»
двойка для
электронов
R – расстояние между
ближайшими атомами.
«Вытягивание»
электронных
облаков при s-p
гибридизации
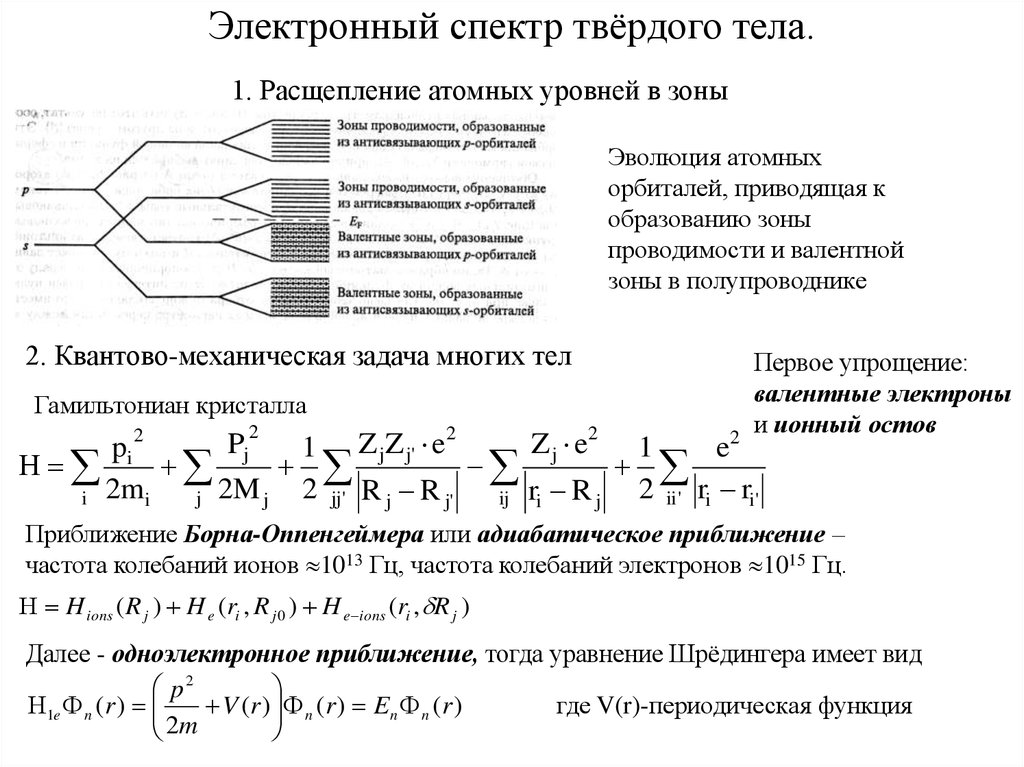
4. Электронный спектр твёрдого тела.
1. Расщепление атомных уровней в зоныЭволюция атомных
орбиталей, приводящая к
образованию зоны
проводимости и валентной
зоны в полупроводнике
2. Квантово-механическая задача многих тел
Гамильтониан кристалла
Первое упрощение:
валентные электроны
и ионный остов
2
2
Pj
Z j e2 1
pi
1 Z jZ j' e
e2
2 jj' R j R j'
2 ii ' ri ri '
i 2m i
j 2M j
ij ri R j
2
Приближение Борна-Оппенгеймера или адиабатическое приближение –
частота колебаний ионов 1013 Гц, частота колебаний электронов 1015 Гц.
H ions ( R j ) H e (ri , R j 0 ) H e ions (ri , R j )
Далее - одноэлектронное приближение, тогда уравнение Шрёдингера имеет вид
p2
1e n (r )
V (r ) n (r ) En n (r )
где V(r)-периодическая функция
2
m
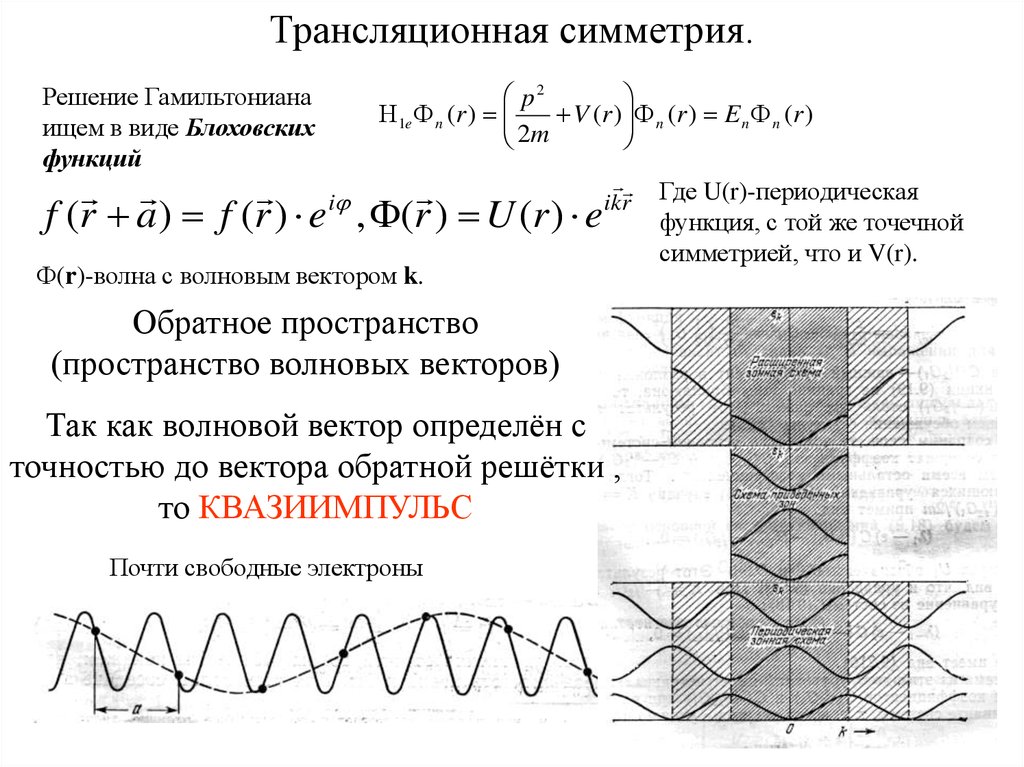
5. Трансляционная симметрия.
Решение Гамильтонианаищем в виде Блоховских
функций
p2
1e n (r )
V (r ) n (r ) En n (r )
2m
i
f (r a) f (r ) e , (r ) U (r ) e ikr
(r)-волна с волновым вектором k.
Обратное пространство
(пространство волновых векторов)
Так как волновой вектор определён с
точностью до вектора обратной решётки ,
то КВАЗИИМПУЛЬС
Почти свободные электроны
Где U(r)-периодическая
функция, с той же точечной
симметрией, что и V(r).
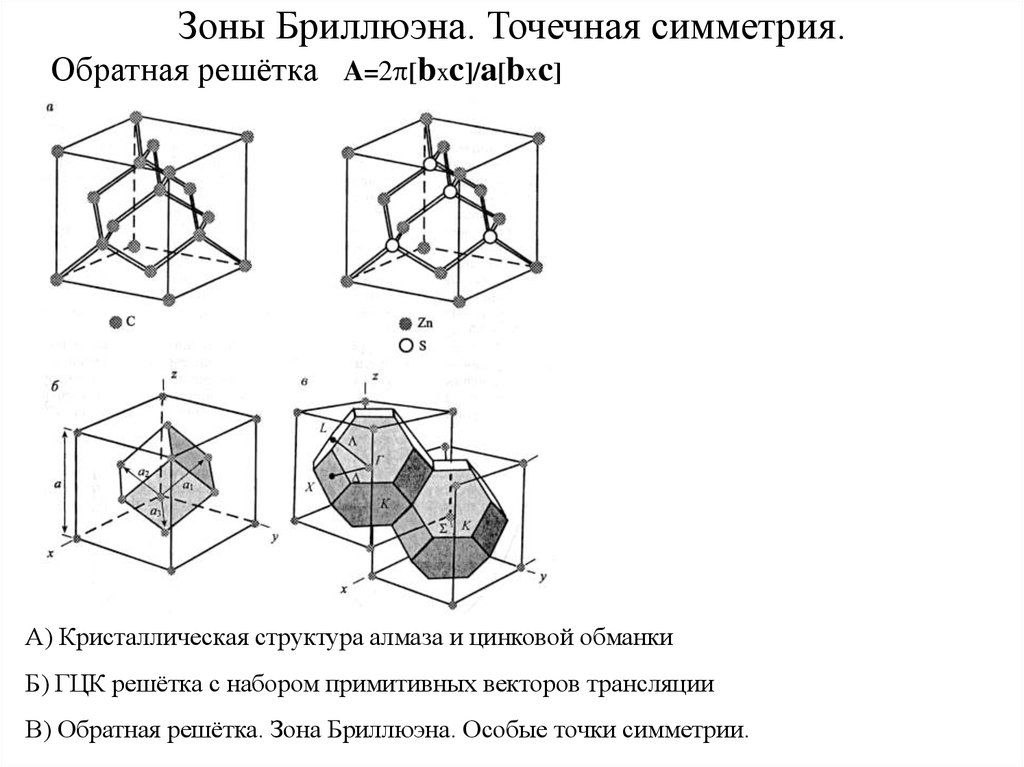
6. Зоны Бриллюэна. Точечная симметрия.
Обратная решётка A=2 [bxc]/a[bxc]А) Кристаллическая структура алмаза и цинковой обманки
Б) ГЦК решётка с набором примитивных векторов трансляции
В) Обратная решётка. Зона Бриллюэна. Особые точки симметрии.
7. Энергетический спектр электрона в кристаллах. Дырки
•Некоторые методы расчёта электронного спектра в кристаллах.Модель почти свободных электронов. Метод сильной связи.
•Минимумы и максимумы энергии в спектре, долины.
•Эффективная масса, изоэнергетические поверхности, анизотропия
эффективной массы.
•Понятие дырки.
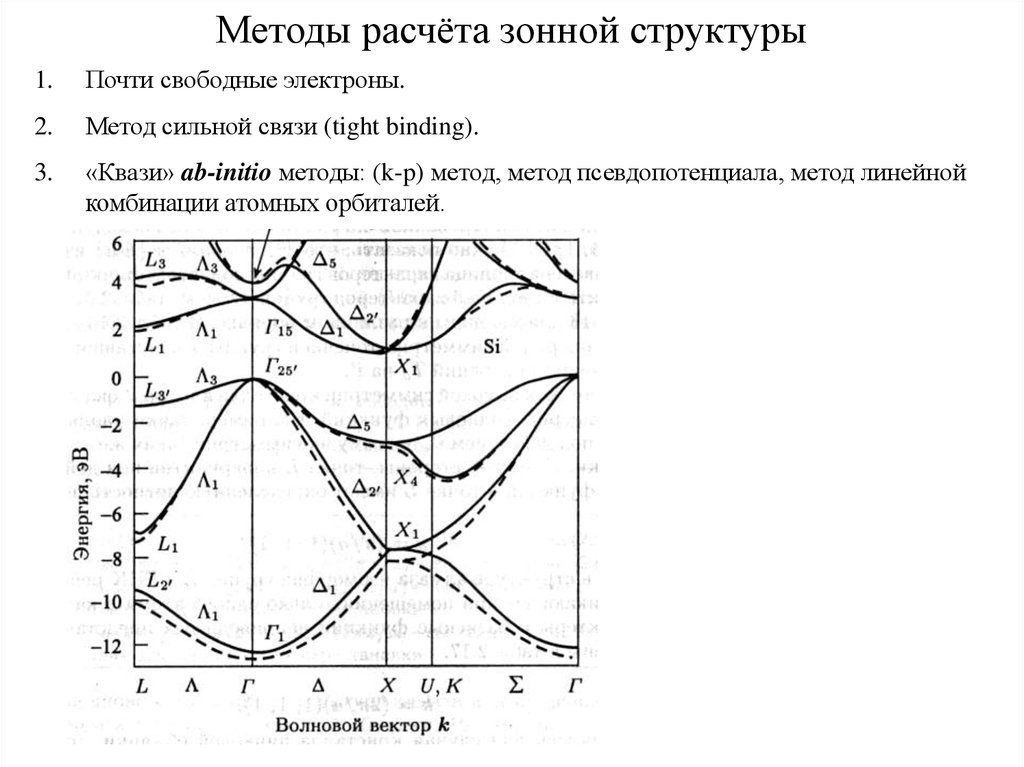
8. Методы расчёта зонной структуры
1.Почти свободные электроны.
2.
Метод сильной связи (tight binding).
3.
«Квази» ab-initio методы: (k-p) метод, метод псевдопотенциала, метод линейной
комбинации атомных орбиталей.
9. Электроны и дырки. Эффективная масса. Анизотропия эффективной массы
kE
2
2meff
mi , j
Изоэнергетические поверхности
в k-пространстве у дна зоны
проводимости в кремнии (слева)
и германии (справа)
( p )
p i p j
p p0
1
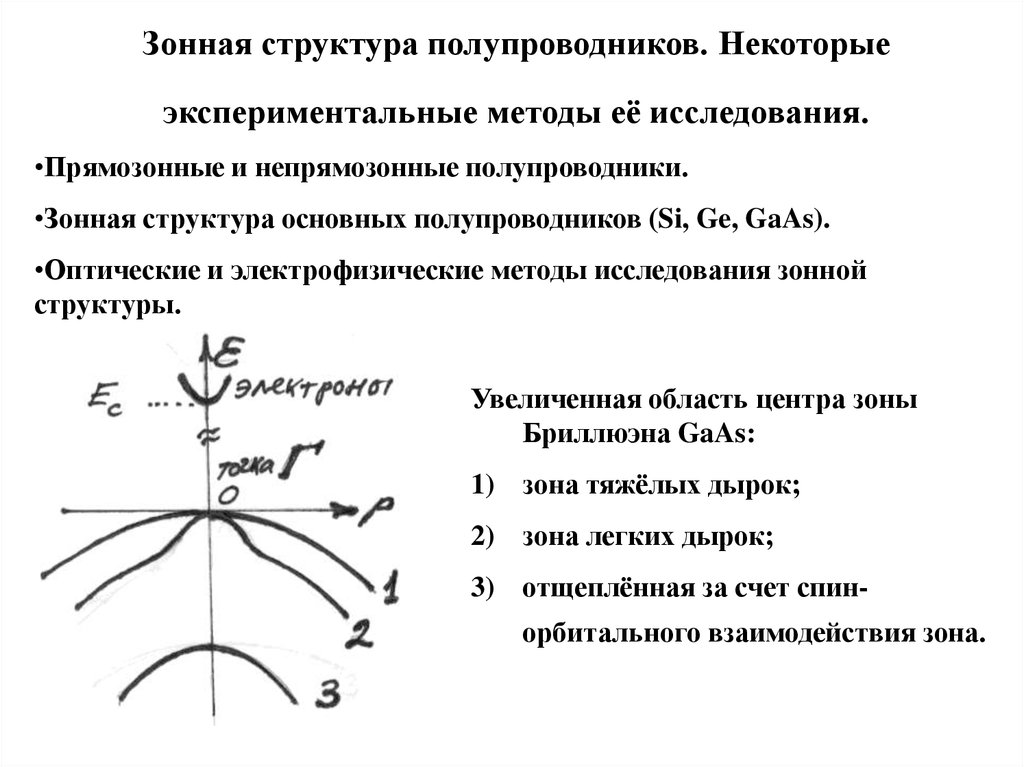
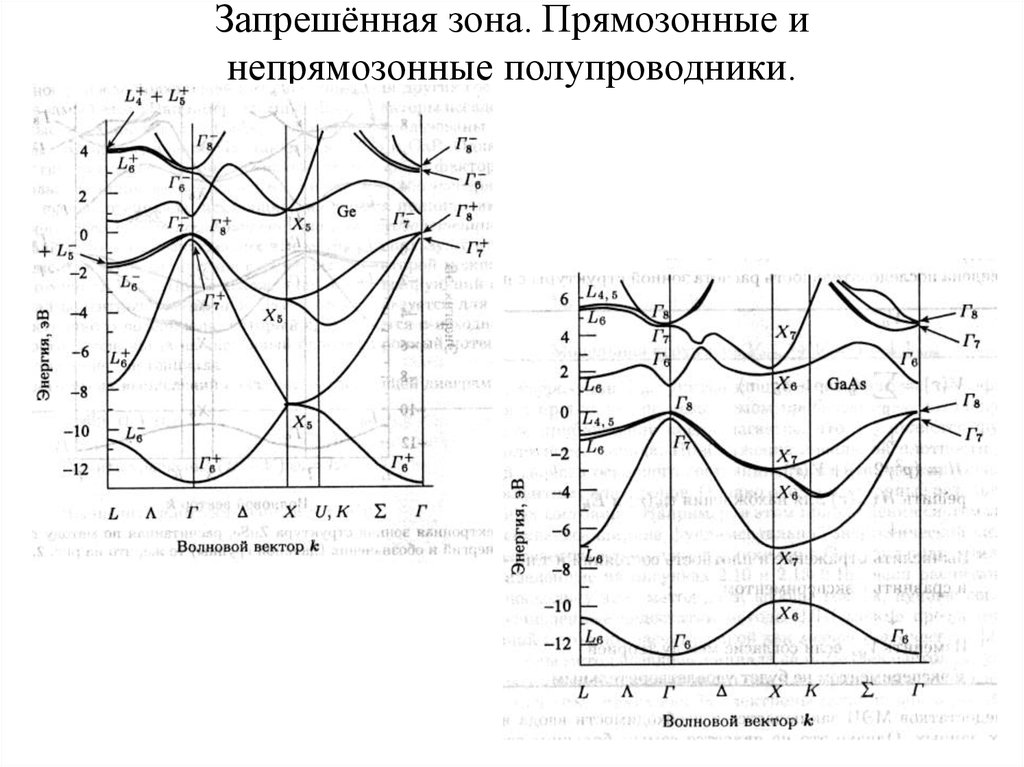
10. Зонная структура полупроводников. Некоторые экспериментальные методы её исследования.
•Прямозонные и непрямозонные полупроводники.•Зонная структура основных полупроводников (Si, Ge, GaAs).
•Оптические и электрофизические методы исследования зонной
структуры.
Увеличенная область центра зоны
Бриллюэна GaAs:
1) зона тяжёлых дырок;
2) зона легких дырок;
3) отщеплённая за счет спинорбитального взаимодействия зона.



 physics
physics








