Similar presentations:
Зонная теория твердых тел. Энергетические уровни свободных атомов
1. Зонная теория твердых тел
Энергетические уровнисвободных атомов
2.
Состояние электронов в атоме определяется 4 квантовымичислами: главным -n , орбитальным - l, магнитным mi- и
спиновым - s. Для атома водорода и водородоподобных атомов n
определяет энергию атомов в стационарных состояниях
( ze 2 ) 2
( n)
2n 2 2
и принимает значения n=1,2….,∞.
Орбитальное квантовое число l определяет орбитальный момент
количества движения электрона
M l (l 1)
l
и принимает значения l=0,1,2……,(n-1).
Магнитное квантовое число mi определяет ориентацию
орбитального момента количества движения
относительно
избранного направления магнитного поля H
M lz ml
ml l , l 1, ..., 0,1, 2,..., l
3.
Спиновое квантовое число s определяет ориентацию собственногомомента
количества
движения
электрона
относительно
H
выделенного направления магнитного поля
M s s ( s 1)
s 1 / 2
Ms
ms
и принимает значение
. Проекция
собственного
момента
ms s, sэлектрона
количества движения
, а ms принимает
значения
.
Состояния l=0 называют s-состояние, l=1 - p-состояние, l=2 (n, l )
d-cостояние.
(n,от
l ) n и l. Так
В многоэлектронных атомах энергия
зависит
как n и l принимают дискретные значения, то и
принимает дискретные значения, разделенные областью
запрещенных энергий.
s-уровень не является вырожденным; p-уровень трехкратно
вырожден. При помещении атома в сильное внешнее поле
вырождение снимается, каждый уровень расщепляется на
z
4.
Обобществление электронов в кристаллеРасположим N атомов Na в виде пространственной решетки на расстояниях,
когда их взаимодействием можно пренебречь. В этом случае атомы можно
считать изолированными.
5.
Энергетический спектр электронов в кристаллеПодобно тому, как основной задачей теории атома
является описание состояний электронов в атоме и вычисление
разрешенных уровней энергии, одна из основных задач теории
твердого тела заключается в определении энергетического
спектра электронов в кристалле. Каждый уровень в кристалле,
состоящем из N атомов, повторяется N раз, т.е. каждый
уровень оказывается N-кратно вырожденным, образуя
энергетическую зону.
Так уровень s дает зону s , состоящую из N подуровней и
способную вместить 2N электронов; уровень p дает зону p,
состоящую из
3N подуровней, способную вместить 6N
электронов.
Наибольшее влияние поле решетки оказывает на
внешние валентные электроны атома, поэтому энергетические
зоны из энергетических уровней этих электронов наиболее
широкие.
6. Модель почти свободных электронов
В этой модели учитывается действие на электроны слабоговозмущающего поля периодического потенциала ионных
остовов. Модель почти свободных электронов позволяет
объяснить общие черты зонной структуры, так и тонкие детали
формы наблюдаемых поверхностей Ферми.
Волновое уравнение для электрона в периодическом
потенциале
Поэтому рассмотрим задачу об электроне в потенциале U (r ) ,
который имеет периодичность решетки Бравэ, лежащей в основе
этой структуры
U (r R) U (r )
8
10
Так как характерный период потенциала ~
см, т.е. совпадает
с длиной волны де-Бройля электрона, то для описания движения
электрона в периодическом потенциале воспользуемся
квантовой механикой.
7.
Нам необходимо изучить те общие свойства одноэлектронногоуравнения Шредингера
2 2
H
U (r )
2m
которые обусловлены периодичностью потенциала U (r ) .
Независимые электроны, каждый из которых удовлетворяет этому
уравнению, называются блоховскими.
Теорема Блоха. Собственные состояния одноэлектронного
гамильтониана
2 2
H
U (r )
2m
R из решетки Бравэ могут быть
, где U (r R) U (r ) при всех
выбраны так, чтобы их волновые функции имели форму плоской
волны, умноженной на функцию с периодичностью решетки
Бравэ, т.е.
i
k
r
n k (r ) e unk (r )
где u (r ) u ( r R )
nk
nk
для всех R из решетки Бравэ.
8.
ik Rn k (r R) e nk (r )
Доказательство. Определим для каждого вектора R решетки Бравэ
оператор трансляции, под действием
которого аргумент
функции f (r ) сдвигается на R .
TR f (r ) f (r R )
В силу периодичности гамильтониана имеем
TR H H (r R) (r R) H (r ) (r R) HTR (r )
Поскольку уравнение
выполняется тождественно для любой
функции (r ) , справедливо следующее операторное тождество
TR H HTR
Результат двух последовательных трансляций не зависит от
порядка их применения, поскольку для любой функции имеем
TR TR (r ) TR TR (r ) (r R R )
9.
поэтомуTR TR TR TR TR R
TR
Таким образом гамильтониан H и операторы
для всех векторов
решетки Бравэ образуют набор коммутирующих операторов. Из
фундаментальной теоремы квантовой механики следует, что тогда
собственные состояния оператора H можно выбрать так, чтобы они
T
одновременно
являлись собственными состояниями
оператора R :
H
TR C (R)
Собственные значения оператора
собой в силу верхнего условия
C (R)
трансляции связаны между
TR TR TR TR С ( R R )
Следовательно, для собственных значений должно выполняться
равенство
С ( R R ) C ( R )C ( R )
10.
Переход из точки r в точку r R можно совершить либонепосредственно, либо путем двух последовательных
трансляций на векторы Rи1 R2, удовлетворяющих условию
R R 1 R2
Волновую функцию ( r R )
в этих случаях можно
представить либо как
(r R) C ( R) (r )
либо как
(r R) C ( R1 ) (r R) C ( R1 ) C ( R2 ) (r )
Отсюда
C ( R) C ( R1 )C ( R2 ).
Следовательно, логарифм коэффициента
аддитивной функцией:
C (R )
ln C ( R ) ln C ( R1 ) ln C ( R2 ).
является
11.
Сопоставляя это выражение счто
R R1 R2 , можно заключить,
C ( R ) e
ik R
Итак, собственные состояния гамильтониана H можно
выбрать
таким образом, что для каждого вектора
решетки
R Бравэ
выполняется равенство
ik R
TR (r R) C ( R) (r ) e (r )
Но это и есть теорема Блоха. Полученному условию
удовлетворяет также функция более общего вида:
.
i
k
r
n k (r ) e unk (r )
12. Граничные условия Борна-Кармана
Граничные условия БорнаКарманаНалагая на волновые
функции соответствующие граничные условия можно
показать, что k должен быть действительным и получить
условия, которым
должны удовлетворять разрешенные значения k . Граничные условия
выбираем так, чтобы они удовлетворяли условию макроскопической
периодичности. Выберем ящик соразмерный элементарной ячейке
соответствующей решетки Бравэ.
Обобщим граничные условия, записав их в форме:
(r N i ai ) (r )
где аi - тройка основных векторов, а Ni - целые числа порядка N1/3 , так что
N=N1N2N3 - полное число элементарных ячеек в кристалле.
Применим к граничному условию теорему Блоха
iN i ai k
nk (r N i ai ) e
nk (r )
i = 1, 2, 3
С учетом граничных условий
e
iN i ai k
1
, i = 1, 2, 3.
13.
Если3
k x1b1 x2b2 x3 b3 xi bi
то
i 1
e
iN i ai
xi bi
e iN i 2 xi 1
Следовательно, должно выполняться условие N i xi mi
- целое число. Поэтому разрешенный блоховский волновой вектор
должен иметь следующий вид
mi
k
bi
i Ni
Отсюда следует, что объем | k |
в k - пространстве, приходящийся
на одно разрешенное значение , равен объему маленького
параллелепипеда с ребрами
:
bi / N i
14.
b b b 1| k | 1 2 3 b1 b2b3
N1 N 2 N 3 N
где b1 b2b3
- объем элементарной ячейки обратной решетки, поэтому
число разрешенных волновых векторов, содержащихся в одной элементарной
ячейке, равно числу ячеек в кристалле.
3
Объем элементарной ячейки обратной решетки равен (2 ) / Vя , где V я V / N
объем элементарной ячейки прямой решетки. Таким образом, объем | k |
в k- пространстве равен
| k | (2 ) 3 / V
Это совпадает с результатом, полученным в теории Зоммерфельда.
Волновое уравнение для электрона в периодическом
потенциальном поле. Разложение периодических функций по
плоским волнам.
В дальнейшем для решения уравнения Шредингера в слабом
периодическом потенциале нам потребуется использовать разложение
периодических функций по плоским волнам. Любую функцию,
подчиняющуюся граничному условию Борна-Кармана, можно разложить
по набору всех плоских волн, удовлетворяющих этому граничному
условию
15.
iq r(r ) c q e
(*)
q
U
(r
) имеет периодичность решетки, поэтому в его разложении
Потенциал
по плоским волнам, будут входить только плоские волны с периодичностью
решетки, поэтому их волновые векторы являются векторами обратной
решетки
i Kr
K
K
где суммирование ведется по всем векторам обратной решетки .
U ( r ) U e
Фурье-коэффициенты U K
1
UK
Vя
1
U0
Vя
связаны с соотношением
iK r
dr e U (r )
по ячейке
dr U (r ) 0
( по ячейке )
U K U K
16.
Пусть кристалл обладает центром инверсии, тогда при определенном выбореначала отсчета U ( r ) U ( r )
; тогда U действительная величина, и
K
поэтому
U K U K U K
Слагаемое с кинетической энергией дает
2
2
2
p
2 iq r
2
q cq e
2m
2m
q 2m
Слагаемое с потенциальной энергией может быть записано в форме
i Kr
iqr
i ( K q ) r
iq r
e
c
cq e U K cq e
U
U
U
q K e
K
K
Kq
K
q
Kq
17.
Заменим обозначения индексов суммирования Kтогда уравнение Шредингера принимает вид
и q на
K
и
q
;
2 2
c
U
0
q e 2m q cq
q K
K
K
iq r
Так как плоские волны, удовлетворяющие условию Борна-Кармана, образуют
ортогональный набор, коэффициент при каждом слагаемом в этом уравнении
должен быть равен нулю, поэтому для всех разрешенных волновых векторов q
получаем
2
2
q
2m
c 0
cq
U
K q K
K
Вставка. Ортогональность различных Фурье-компонент:
dxe
ik x ikx
e
1
i ( k k ) L
e
1
0
,
если
k
k
;
i (k k )
L, если k k
Умножим обе части предыдущего уравнения на и проинтегрируем получим последнее уравнение.
18.
qk
K
Удобно записать
в форме
, где K - вектор обратной
решетки, выбранный так, чтобы вектор k лежал в первой зоне Бриллюэна.
Уравнение тогда имеет вид
q
2 2
(k K )
2m
c 0
ck K
U
K k K K
K
или, если сделать замену переменных
2 2
(k K )
2m
K K K
,
c 0
ck K
U
K K k K
K
(1)
Это уравнение является самым важным
уравнением зонной теории
твердого тела. При фиксированном k
из первой зоны Бриллюэна
K
система уравнений (1) при любом значении вектора обратной решетки
связывают между собой только коэффициент Фурье с к
компонент
плоской волны какой-либо конкретной орбитали с бесконечным числом
других коэффициентов
Фурье ck K , ck K , ck K ,...,
у которых волновые
векторы k отличаются от на вектор обратной решетки для всех других
плоских волн, которые входят в ряд Фурье этой орбитали.
19.
.K
K0
Обозначим через
наименьший из векторов обратной решетки
Предположим, что выражение для потенциальной энергии содержит лишь
один член, т. е. одну компоненту Фурье U K 0 U K 0
, которую обозначим
через
. Тогда система (1) для фиксированного k
будет содержать
0
лишь три уравнения:
U
2 k 02
c k U c k K c k K 0,
0
0
0
0
0
2
m
2 (k 0 K 0 ) 2
c U c c 0,
k0 2 K 0
k0
k0 K 0
2
m
2 (k 0 K 0 ) 2
c U c c 0.
k0
k0 2 K 0
k0 K 0
2
m
k 0 на k 0 K 0
Видно, что второе и третье уравнения получаются из первого заменой
c k 2K
cиk 2K
. Коэффициенты
становятся связанными между
0
0
0
0
с k с K
собой и следует выписать еще два уравнения
и т.д. до
0
0
бесконечности.
20.
Следовательно, исходная задача распаласьна N независимых задач – для
каждого разрешенного значения k
в первой зоне Бриллюэна. Каждая
такая задача имеет решение, которое является
суперпозицией плоских волн,
содержащих только волновой вектор k и волновые векторы, отличающиеся от k
на какой-либо вектор обратной решетки.
Используя полученные результаты, вернемся к разложению волновой функции
(*). Видно, что волновой вектор q принимает лишь значения k , k K , k K , ...,
а волновая функция имеет следующий вид
i(k K )r
e
k (r )
c
k K
K
Если переписать это выражение как
ik r
i Kr
e
k (r ) e
c
k
K
K
то видно, что функция имеет блоховскую форму
i
k
r
n k (r ) e unk (r )
21.
Где периодическая функция u(r) дается выражениемiK r
k K
K
u (r ) c
e
.
k
При фиксированном
существует бесконечно много решений
системы уравнений (1). Для их перечисления используют номер зоны
n.
Импульс электрона в кристалле
В модели свободных электронов
импульс электрона p k . В блоховском
случае волновой вектор k не пропорционален импульсу электрона. Это
следует из того, что гамильтониан в присутствии неоднородного
потенциала не обладает полной трансляционной инвариантностью.
Действительно, подействовав оператором импульса
на
, получим
p i
nk
ik r
ik r
ik r
i nk i [e unk (r )] k e unk (r ) i e unk (r ) k nk (r ) i e unk (r )
ik r
Это уравнение не имеет вида соnst nk
, т.е. nk не является собственным
состоянием оператора импульса. Тем не менее, часто k служит естественным
обобщением импульса на случай периодического потенциала.
22.
kЧтобы подчеркнуть сходство и указать отличие
от истинного
импульса, эту величину называют квазиимпульсом электрона. Волновой вектор
, входящий в теорему Блоха, можно всегда считать относящимся к первой
зоне Бриллюэна. Это справедливо потому, что если вектор
не лежит в
k
первой зоне Бриллюэна, то его можно представить в виде
,
k
K
k k K
k
в первой зоне
где вектор обратной решетки, а вектор
лежит
iK R
Бриллюэна. Для любого вектора обратной решетки
, поэтому
e 1
если соотношение Блоха выполняется для k
, то оно справедливо и для . k
Уровни энергии электрона в периодическом потенциале.
Номер зоны n появляется в теореме Блоха из-за того, что при заданном
значении k
имеется много решений уравнения Шредингера.
Будем искать все решения уравнения Шредингера , которые могут быть
представлены в блоховской форме
ik r
с заданным волновым вектором
периодичностью решетки.
k
(r ) e u (r )
и с функцией
u , обладающей
23.
Подставляя это выражение в уравнение Шредингера, находим, чтоопределяется задачей на собственные значения
u
2
2
H k u k ( r )
k i U (r ) uk (r ) k uk (r )
2m
с граничным условием
uk (r ) uk (r R )
k
Можно считать, что энергия уровней
меняется
с волновым вектором
непрерывно с волновым вектором k
. В результате мы приходим к
описанию уровней энергии в периодическом
потенциале посредством
семейства непрерывных функций n (k )
. То обстоятельство,
что в силу
граничного условия Борна-Кармана волновой вектор k
может принимать
лишь дискретные значения, не имеет отношения
к непрерывности n (k )как
функции от непрерывной переменной k
, поскольку в задачу на
собственные значения не входит размер всего кристалла и она имеет смысл
при любом k .
n ,k K (r ) n ,k (r ),
n ,k K nk .
24.
Таким образом, энергетические уровни электрона в решетке впериодическом
потенциале
описываются посредством семейства
, каждая из которых имеет
непрерывных функций n (k )
или
nk
периодичность обратной решетки. Эти функции определяют зонную
структуру твердого тела.
Совокупность всех электронных уровней, описываемых функцией n (k ) при
фиксированном
n , называют энергетической зоной. Каждая функция (k )
n
периодична по k
и непрерывна,
у
нее
существуют
верхний
и
нижний
пределы и все уровни
лежат в зоне энергий между этими
n (k )
пределами.
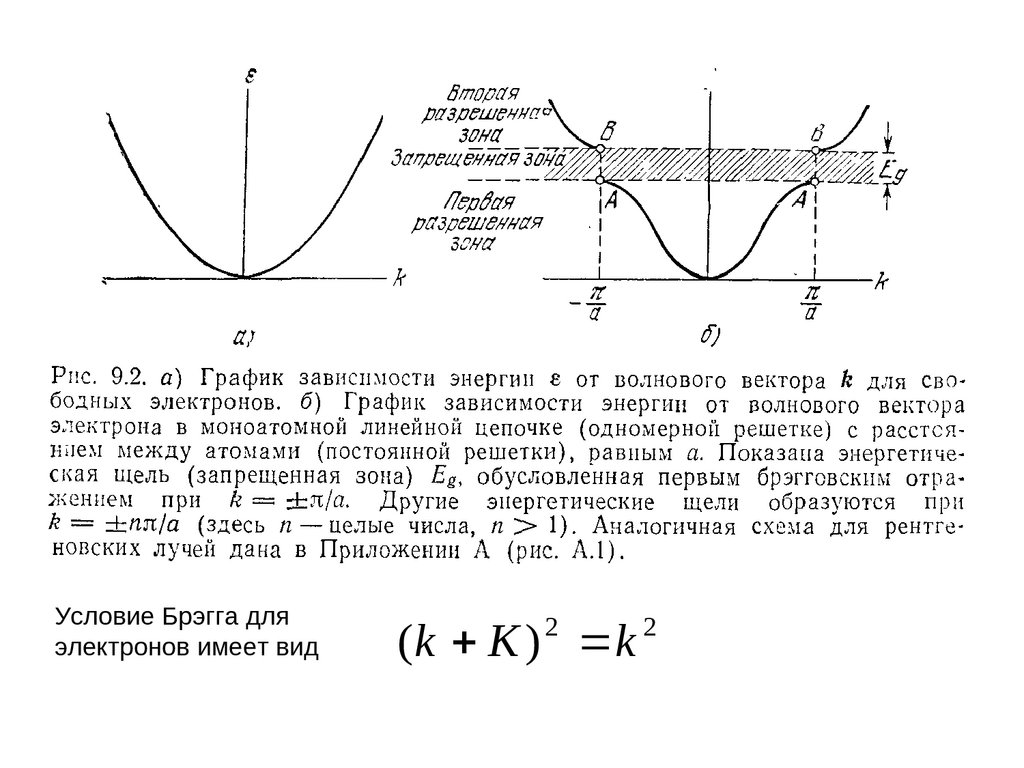
Происхождение запрещенной зоны
Попытаемся понять физические причины наличия запрещенных зон,
рассматривая для начала
простую
модель кристалла
в
виде
линейной
цепочки атомов (одномерной решетки), расположенных на
расстоянии а один от другого (а — постоянная решетки).
25.
Условие Брэгга дляэлектронов имеет вид
2
2
(k K ) k
26.
В одномерном случае условие Брэггадает следующий набор значений :
1
k K n / a
2
где
e i x / a
K n2 / a
-обратная длина (в общем случае
— вектор обратной решетки), n —
целое число. Первые отражения (и
первая энергетическая щель)
имеют место при k / a
(n=1); последующие
энергетические щели отвечают
другим значениям n,
соответствующим n > 1
При k = ± / a волновые функции
электрона уже не являются
i x / a
бегущими волнами вида e
и
, как это было в модели
свободных электронов.
27.
Решения при этих частных значениях k представляют собой совокупности равногочисла волн, распространяющихся вправо и влево, т. е. являются стоячими
волнами. Приведем лишь некоторые качественные соображения. Когда условия
Брэгга удовлетворяются, можно сказать, что волна, бегущая в одном направлении,
испытав брэгговское отражение, распространяется затем в пpoтивоположном
направлении. Каждое последующее брэгговское отражение вновь обращает
направление распространения волны. Единственной независимой от времени
картиной, отвечающей такой ситуации, является картина образования стоячих
волн. Из бегущих волн вида e i x / a
и e i x / a , мы можем сформировать две
различные стоячие волны, а именно:
( ) e
i x / a
e
i x / a
( ) e i x / a e i x / a
2 cos
x
,
a
x
2i sin
.
a
Стоячие волны состоят из бегущих - правых и левых в равных долях. Индексы
(+) и (-) у стоячих волн означают соответственно четную и нечетную функции
при замене х на -х.
28.
Две стоячие волны ( )и ( ) отвечают группировке электронов в различных поотношению к ионам областях пространства, а, следовательно, эти две волны
имеют различные значения потенциальной энергии. Это обстоятельство и
является причиной существования энергетической щели. В квантовой механике
2
плотность вероятности (x)
нахождения частицы в точке х равна (x)
.
Для чисто бегущих волн функция ~ e ikx
и, следовательно,
( x) e ikx e ikx 1
, т.е. плотность заряда — постоянная величина. Но для линейной комбинации
(x )
плоских волн плотность заряда уже не будет
( )постоянной величиной.
Рассмотрим, например, стоячую волну
; для плотности
в этом
случае получим:
x
2
( ) ( ) ~ cos 2
a
.
Эта функция описывает скопление отрицательного заряда на положительных
ионах или вблизи них, т. е. в областях x 0, a, 2a,...
, где потенциальная
энергия — наименьшая.
29.
30.
В стоячей волне для плотности вероятности имеем:x
( ) ( ) ~ sin
a
2
2
Эта функция описывает такое распределение электронов, при котором они
располагаются преимущественно в областях, соответствующих серединам
расстояний между ионами, т. е. вне ионных остовов. При расчете средней
потенциальной энергии для каждого из описанных трех случаев распределения
электронной плотности следует ожидать, что в случае
средняя
( )
потенциальная энергия будет меньше, чем для бегущих волн, в то время как
для ( ) она соответственно больше. Если средние значения потенциальной
энергии для ( ) и ( )
различаются на величину Eg, то существует
энергетическая щель шириной Eg . Волновая функция ( )
(ниже
( )
энергетической щели) отмечает на рис. 9.2 точкам А, а волновая функция
(выше энергетической щели) - точкам В.
31. Поверхность Ферми
Основное состояние N свободныхэлектронов строится путем заполнения всех
одноэлектронных уровней k с энергиями
( k ) 2 k 2 / 2 m
, меньшими F
где F
определяется из условия, что полное число
одноэлектронных уровней с энергией F
, должно быть равно полному числу
электронов.
Основное состояние
N блоховских электронов строится аналогичным образом,
за исключением
того, что одноэлектронные уровни задаются теперь квантовыми
n (k )
числами n и k , а
уже не определяется простым выражением как в
теории свободных электронов. После заполнения низших уровней определенным
числом электронов могут получиться конфигурации двух различных типов.
F
F
1. Некоторые зоны могут оказаться полностью заполненными, а все остальные –
пустыми. Разность энергий между самым высоким занятым уровнем и самым
низким незанятым уровнем (т.е. между «вершиной» самой верхней занятой зоны и
«дном» самой низкой пустой зоны) называют запрещенной зоной. Твердые тела, у
которых ширина запрещенной зоны значительно больше k B T , представляют
собой диэлектрики.
32.
k B T , то такие твердые телаЕсли ширина запрещенной зоны сравнима с
называют собственным полупроводником. Поскольку число уровней в зоне равно
полному числу элементарных ячеек в кристалле и на каждом уровне могут быть
размещены два электрона, то для возникновения конфигурации с запрещенной
зоной необходимо, чтобы число электронов в расчете на одну элементарную
ячейку было четным.
2. Некоторые зоны могут оказаться заполненными частично. Когда это имеет
место, энергия наиболее высокого заполненного уровня, т.е. энергия Ферми,
лежит внутри области энергий одной или более зон. В k -пространстве каждой
частично заполненной зоне соответствует поверхность, отделяющая занятые
уровни от незанятых. Все такие поверхности называют поверхностью Ферми.
Поверхность Ферми для блоховских электронов является обобщением сферы
Ферми, рассмотренной ранее для свободных электронов. Части поверхности
Ферми, соответствующие отдельным частично заполненным зонам, называют
полостями поверхности Ферми.
Аналитическое определение полости поверхности Ферми в n-той зоне таково:
n (k ) F
Следовательно, поверхность Ферми представляет собой поверхность
постоянной
энергии (или совокупность
поверхностей постоянной энергии) в k -пространстве.
Поскольку функции n (k ) периодичны в обратной решетке, полное решение этого
уравнения для каждого n представляет поверхность в k -пространстве, также
обладающей периодичностью обратной решетки.
33. Общий подход к уравнению Шредингера в случае слабого потенциала
Когда периодический потенциал равен нулю, решения уравнения Шредингерапредставляют собой плоские волны. В случае слабого периодического
потенциала волновую функцию блоховского уровня с квазиимпульсом можно
записать в форме
i(k K )r
e
k (r )
c
k K
K
, где коэффициенты
уравнений
c k K
и энергия уровня
определяются системой
.
2 2
(k K )
2m
c 0
ck K
U
K K k K
K
(1)
В случае свободных электронов все Фурье-компоненты U K равны нулю.
Уравнение примет вид
2
2
0
0
k K (k K )
(*)
где
k K
k K
2m
c
0
34.
Из уравнения (*) следует, что для любого K должно выполняться условиеc k K
=0
0
или условие k K 0
K
. Последнее может иметь место лишь для
одного
, кроме случаев,
имеет одно и то же значение при
нескольких различных значениях K . Если такое вырождение отсутствует, то
получаем обычные решения для свободных электронов:
k0 K 0
0
когда
k K
k (r ) ~ e i ( k K ) r
Если, однако, имеется такая группа волновых векторов
обратной решетки, для которых
K1 , . . . , K m
k0 K 1 ... k0 K m
(**),
то при энергии
, равной значению (**), существует m независимых
вырожденных решений вида плоской волны. Поскольку любая линейная
комбинация вырожденных решений также является решением,
остается
полная
c
свобода в выборе коэффициентов
при . K K , ... , K
k K
1
m
Эти простые замечания приобретают более глубокое содержание, если
значения U K не равны нулю, но очень малы.
35.
Cчитаем, что энергия двух и более различных уровней свободных электроновравны друг другу с точностью до членов
порядка U .
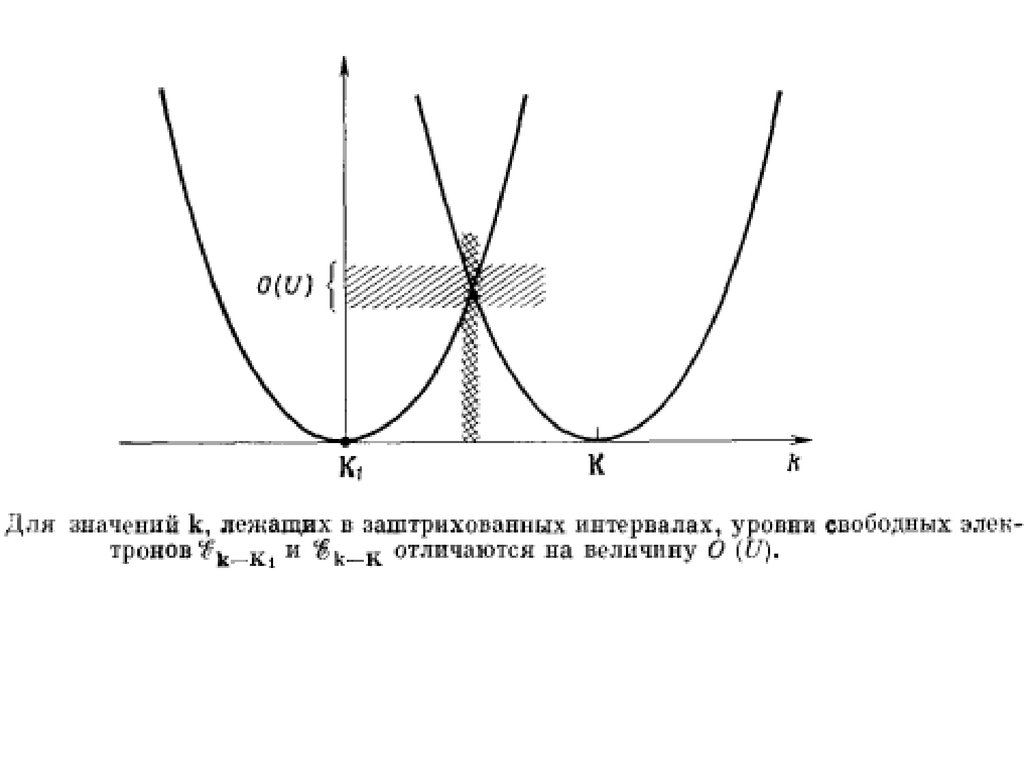
Случай 1. Будем считать вектор k фиксированным и рассмотрим такой вектор
K1 обратной решетки, для которого выполняется условие
для заданного
k K1
k
k0 K1 k0 K U
и всех K
K1 , т.е. энергия свободного электрона при
отличается от его значения при всех других K на величину,
значительно превышающую U (Рис.) .
Будем рассматривать воздействие потенциала на такой уровень свободного
электрона, для которого
0
k K1
, сk K 0, K K1.
Полагая в уравнениях (1)
и используя обозначение (*), находим
(штрих у индекса суммирования опускаем)
0
(2)
K K1 k K
k K1
k K1
K
Поскольку мы выбрали аддитивную постоянную в потенциальной энергии таким
образом, чтобы U K 0
при K = 0, в правой части уравнения имеются
только члены с K
K.
c
1
U
c
36.
ck K 0Так как мы рассматриваем
решение, для которого
обращается
в нуль при K K1 в пределе U → 0, следует ожидать, что члены в правой
части уравнения будут иметь второй порядок малости по U (рис).
Это можно
проверить непосредственно, записав уравнение (1) для
K K1 в виде
c k K
U K 1 K c k K
1
0
k K
U K K c k K
K K1
0
k K
(***)
В отсутствие приближенного вырождения имеем
ck K
U K 1 K ck K
2
1
O
(
U
).
0
k K
Подставляя это выражение в (2), находим
( k0 K )ck K
1
1
K
U K K 1U K 1 K
k0 K
ck K O(U 3 ).
1
37.
38.
Следовательно, возмущенный уровень энергииотличается от значения 0
k K1
для свободного электрона на величину порядка
. Поэтому, чтобы
U2
0 для
решить уравнение
с такой точностью, достаточно заменить
справа
в знаменателе на k K1 ; в результате получаем следующее выражение для
с точностью до второго порядка поU :
2
(3)
U
k0 K 1
K
K K1
k0 K 1 k0 K
O(U 3 ).
Уравнение (3) показывает, что слабо возмущенные невырожденные зоны
0
0
отталкивают друг друга: каждый уровень k K
, лежащий ниже k K 1
,
дает вклад в (3), повышающий величину
, а каждый уровень,
0
расположенный выше
, дает вклад, понижающий эту энергию.
k K1
Однако наиболее важный качественный вывод, который следует из этого
анализа, заключается в том, что сдвиг энергии по сравнению со значением для
свободных электронов имеет второй порядок малости по энергии U.
39.
Случай 2.Пусть величина k такова, что имеются векторы K1 , ... , K m обратной решетки,
для которых энергии 0 ... 0
k K1
k Km
отличаются друг от друга на величину порядка U , тогда разность между этими
энергиями и энергией 0
велика по сравнению с U ,
k K
0
0
k K k K U , i 1, . . . , m, K K1 , . . . , K m
i
В этом случае
мы должны рассматривать отдельно
те из уравнений системы (1),
для которых K есть одно из m значений K1 , ... , K m . Это дает m уравнений,
соответствующих уравнению (2) в невырожденном случае. В получаемых m
уравнениях выделяем из суммы те члены, которые содержат коэффициенты
ck K , j 1, . . . , m
j
Эти члены могут и не быть малыми в пределе стремящегося к нулю
взаимодействия в отличие от других членов, которые имеют порядок выше U . В
результате получим .
(
0
k Ki
m
)ck K U K j K i ck K
i
j 1
j
K K1 , . . . , K m
U K K i ck K , i 1, . . . , m
(****)
40.
Выделяя таким же образом члены в сумме, можно записать уравнение (1) дляостальных уровней в виде
ck K
1
k0 K
m
U c U c , K K1 , . . . , K m
j 1 K j K k K j K K , . . . , K K K k K
1
m
(4)
Последнее уравнение соответствует уравнению (***)в случае отсутствия
приблизительного вырождения.
Поскольку при
имеют порядок выше
K K1 , . . . , K m коэффициенты c k K
U , уравнения (4) дают
ck K
1
k0 K
m
U
j 1
Подставляя эти выражения в (****), получим
.
(
0
k Ki
m
)ck K U K j K i ck K
i
j 1
O(U 2 )
U K K i U K j K
c O(U 3 )
k0 K k K j
j 1 K K1 , . . . , K m
(5)
m
j
c
Kj K k Kj
41.
Сравним полученные уравнения с результатом (3) для случая, когдаприблизительное вырождение отсутствует. Там было получено явное
выражение для сдвига энергии с точностью до U 2 (система уравнений (5)
переходит в него при m=1 ). Теперь, однако, видно, что с точностью до U 2
определение сдвигов для m почти вырожденных уровней сводится к решению
системы из m уравнений для ck K i . При этом коэффициенты во второй сумме
справа в этих уравнениях имеют более высокий порядок по U , чем в первой.
Следовательно, чтобы найти основные поправки по величине U , можно
заменить (5) системой гораздо более простых уравнений:
m
( k0 K )ck K U K j K i ck K , i 1, . . . , m
i
i
j 1
(6)
j
представляющих собой просто общие уравнения для системы с квантовыми
уровнями.
42.
Энергетические уровни вблизи одной из брэгговских плоскостейПростейшим и наиболее важным примером предыдущего анализа является
случай, когда два уровня свободных электронов расположены близко друг к
другу (по сравнению с U ), но далеко от остальных уровней (также по сравнению
с U ). Если это так, то уравнения (6) сводятся к двум уравнениям
0
K
k K1
k K1
2 K1 k K 2
(7)
0
K1 K 2 k K1
k K2
k K2
(
)c
U
c
(
)c
U
c
,
Поскольку речь идет о двух уровнях, то нет необходимости пользоваться
симметричными обозначениями. Введем переменные, удобные для
двухуровневой задачи
q k K 1 и K K 2 K 1
, и запишем уравнение (7) в виде
0
q
( )cq U K cq K ,
(
0
q K
)c
q K
(8)
U c U c .
K q
K q
43.
44.
Справедливы следующие соотношения:K K , 0.
q 0 q K , q 0 q K U
(9)
при
0
0
Энергия q
равна q K
для некоторого вектора
обратной решетки,
только в случае, если выполняется условие | q | | q K |
Это означает (рис. a), что точка q лежит на брэгговской плоскости, которая
перпендикулярна
отрезку, соединяющему начальную точку в k-пространстве с
точкой K обратной решетки, и делит этот отрезок пополам.
С геометрической точки зрения условие (9) означает, что точка q
должна быть
близка к одной брэгговской плоскости (но далека от места пересечения двух и
более брэгговских плоскостей). Следовательно, случай двух почти вырожденных
уровней относится к электрону, волновой вектор которого почти точно
удовлетворяет условию однократного брэгговского рассеяния. Слабый
периодический потенциал сильнее всего влияет на почти вырожденные уровни,
поэтому главное воздействие слабый периодический потенциал оказывает лишь
на те уровни свободного электрона, волновые векторы которых близки к
векторам, допускающим брэгговское отражение.
45.
Изучение структуры энергетических уровней, возникающих в слабом потенциале,начнем с рассмотрения случая, когда существенна лишь одна брэгговская
плоскость и структура уровней определяется уравнениями (8). Эти уравнения
имеют решение при выполнении условия
q 0
U
K
U K
из которого следует квадратное уравнение
0
q K
0,
0
q
( )(
2
0
0
q q K
Его два корня
1 0
0
U
( q q K )
K
2
2
2
0
q K
) U
2
K
1/ 2
(10)
описывают
результат воздействия периодического потенциала на два
0 главный
0
q близка к
уровня q
и q K свободных электронов, когда
точка
брэгговской плоскости, определяемой вектором K ( Рис.).
0
q
q
Если принадлежит брэгговской плоскости,
q 0 U K
,
(11)
q
если
лежит на одной брэгговской плоскости.
0
= q K . Следовательно,
46.
47.
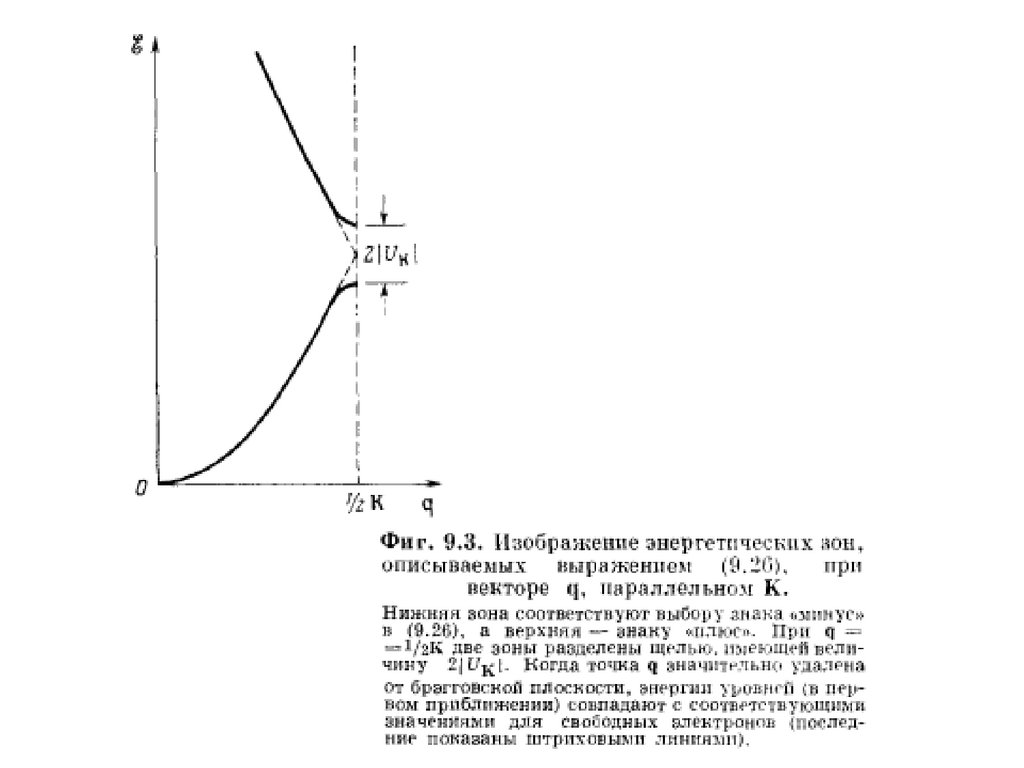
Таким образом, для всех точек на брэгговской плоскости один из уровнейповышается на величину U K , а второй понижается на ту же постоянную
величину.
0
0
Исходя из (10) можно также показать, что при q = q K выполняется
соотношение
2 1
q
K
;
q m
2
т.е. если точка q лежит на брэгговской плоскости, то градиент параллелен
этой плоскости (рис. б). Поскольку градиент перпендикулярен изоэнергетическим
поверхностям, то эти поверхности перпендикулярны брэгговской плоскости.
Если точка q принадлежит одной брэгговской плоскости, то можно также
определить вид волновых функций, отвечающих двум решениям
0
q U K
Из (8) следует, что если дается выражением (11), то два коэффициента
сq0 и сq0 K удовлетворяют соотношению
.
0
q
K
q K
c sign U
c
Поскольку два этих коэффициента доминируют в разложении волновой функции
блоховского уровня по плоским волнам, получим в первом приближении
iq r
i(q K )r
k (r ) c q e c q K e
(12)
48.
Условие двухкомпонентного представления волновой функции2
q
c c
2
q K
2
, q ( q K )
2
Это условие совпадает с известным правилом Вульфа-Брэгга для отражения
электронов и рентгеновских лучей. Брэгговское отражение объясняет
физический смысл двухкомпонентного приближения: в составлении волновой
функции равноправно участвуют падающий и дифрагированный пучки.
При U 0
с учетом (12)
K
2
2
1
(r ) ~ cos Kr , q 0 U K ,
2
2
2
1
(r ) ~ sin Kr , q 0 U K .
2
Это следует из того, что на брэгговской поверхности, где
1
1
1
i Kr
i Kr
ik r
i(k K )r
2
k K k (r ) c k e c k K e
c k e
c k K e 2
2
49.
ЕслиU K 0,
то
2
2
1
(r ) ~ sin Kr , q 0 U K ,
2
2
2
1
(r ) ~ cos Kr , q 0 U K .
2
Иногда два найденных типа линейных комбинаций называют волновыми
функциями «s-типа»
2
1
2
(r ) ~ cos Kr
2
и «p-типа»
2
2 1
(r ) ~ sin Kr
2
, учитывая их зависимость от координат вблизи точек решетки. Комбинации sтипа, как и для атомных s-уровней, не обращаются в нуль на ионе; в
комбинации р-типа плотность заряда для малых расстояний изменяется
пропорционально квадрату расстояния от иона и обращается в нуль на ионе,
что характерно для атомных р-уровней.
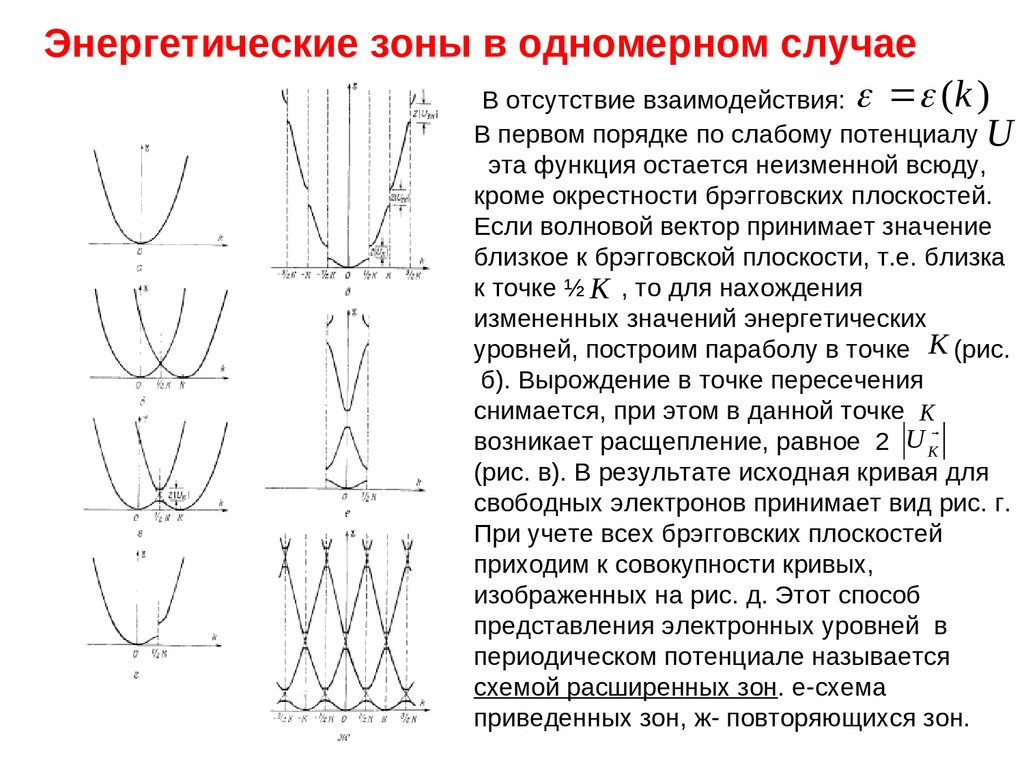
50. Энергетические зоны в одномерном случае
В отсутствие взаимодействия: (k )В первом порядке по слабому потенциалу U
эта функция остается неизменной всюду,
кроме окрестности брэгговских плоскостей.
Если волновой вектор принимает значение
близкое к брэгговской
плоскости, т.е. близка
к точке ½ K , то для нахождения
измененных значений энергетических
уровней, построим параболу в точке K (рис.
б). Вырождение в точке пересечения
снимается, при этом в данной точке K
возникает расщепление, равное 2 U K
(рис. в). В результате исходная кривая для
свободных электронов принимает вид рис. г.
При учете всех брэгговских плоскостей
приходим к совокупности кривых,
изображенных на рис. д. Этот способ
представления электронных уровней в
периодическом потенциале называется
схемой расширенных зон. е-схема
приведенных зон, ж- повторяющихся зон.
51.
Энергетическая щельВ общем случае слабый периодический потенциал приводит к энергетической
щели вблизи брэгговских плоскостей. Действительно, если U K 0 , то при
пересечении волновым вектором брэгговских плоскостей, совершается
U K 0
непрерывный переход с одной ветви на другую, как показано на рис. б.
Если
, то это уже не так. Теперь при переходе волнового вектора через
брэгговскую плоскость энергия изменяется непрерывно только в том случае,
если мы остаемся на кривой, отвечающей нижней или верхней ветви (рис. в).
Чтобы перейти с одной ветви на другую при непрерывном изменении
,
U K
энергия должна изменяться скачком по крайней мере на величину
2
.
k
Число уровней в зоне
Рассмотрим одномерный (линейный кристалл) с постоянной решетки, равной а ;
такой кристалл построен из N элементарных ячеек длиной L. Чтобы подсчитать
число возможных состояний введем периодические граничные условия для
волновых функций, а именно, длину блока периодичности будем считать равной
длине цепочки. Разрешенные значения волнового вектора электрона в первой
2
4
N
зоне Бриллюэна принимают значения:
k 0; ; ;...;
.
(5.34)
L
L
L
N
Этот ряд ограничен значением k
, поскольку k
служит границей
L
a
a
зоны Бриллюэна.
52.
Таким образом, полное число значений k точно равно N- числу элементарныхячеек. Отсюда следует, что каждая элементарная ячейка в каждой энергетической
зоне дает точно одно независимое значение k. Это утверждение переносится и на
случай трех измерений. С учетом того, что каждый электрон может иметь одну из
двух спиновых ориентаций, общее число независимых состояний (орбиталей) в
каждой энергетической зоне равно 2N.
Если на каждую элементарную ячейку приходится один атом одновалентного
элемента, то в энергетической зоне будет занято электронами ровно половина
состояний (уровней). Если кристалл состоит из атомов двухвалентного элемента,
и каждый атом может отдать два электрона, то зона будет заполнена целиком.
Пусть в элементарной ячейке кристалла Z электронов. Тогда общее число
электронов в решетке равно zN. При достаточно низкой температуре они займут
первые zN энергетических уровней. Таким образом, число заполненных зон равно
zN z
2N 2
z 2n
Если
(четное число), то все зоны, содержащие электроны, полностью
ими заполнены, энергия Ферми совпадает с верхней границей одной из зон.
53.
Металлы и диэлектрикиЕсли валентные электроны заполняют целиком одну или более верхних
разрешенных зон, то кристалл является диэлектриком. В таком кристалле
наложение внешнего электрического поля не приводит к появлению
электрического тока. Если целиком заполненная зона отделена от следующей
более высокой зоны энергетической щелью, то нет никакого способа непрерывным
образом изменить суммарный импульс электронов кристалла. Все разрешенные
состояния заняты и наложение поля ничего не может изменить. Ситуация совсем
иная, чем в случае свободных электронов (смещение сферы Ферми в
электрическом поле).
Другой подход к анализу этой ситуации состоит в использовании уравнения
движения:
dk
.
dt
F
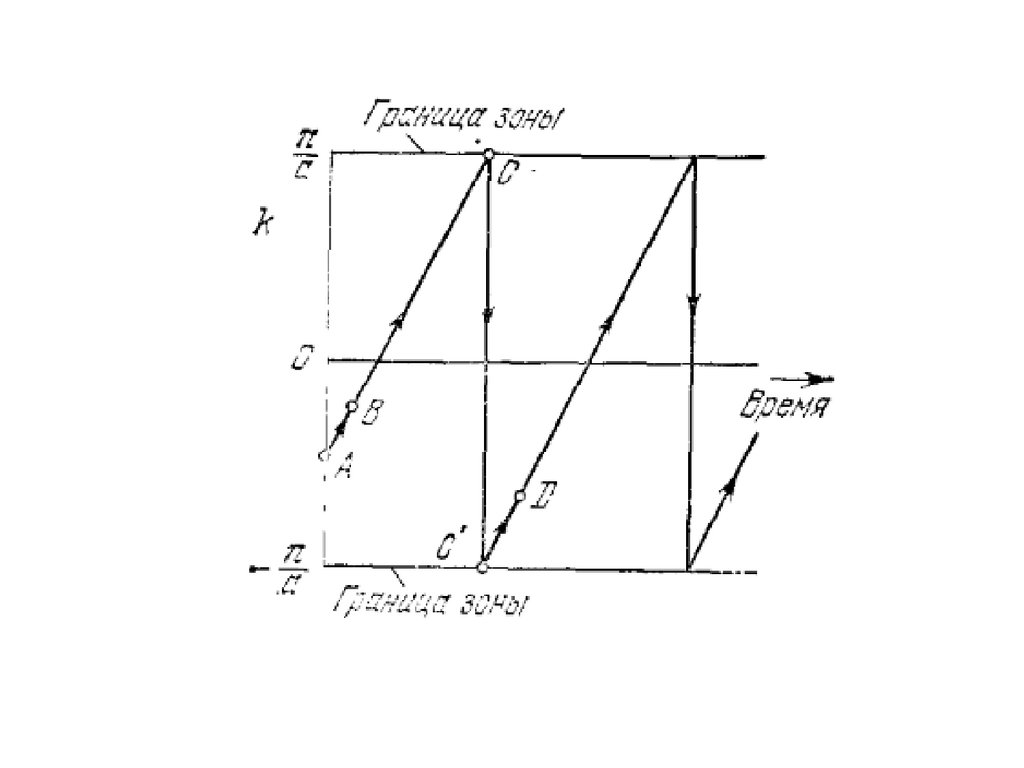
Под действием постоянной силы волновой вектор электрона
будет
непрерывно увеличиваться с течением времени. Но когда k (t ) , возрастая,
достигнет границы зоны, волновой вектор испытает «переброс» (рис.) на
противоположную границу.
Это движение будет происходить вновь и вновь, но не приведет к какому-либо
результирующему ускорению, в чем можно убедиться, если провести
усреднение по всем состояниям зоны.
Любой кристалл может быть диэлектриком при четном числе валентных
электронов в элементарной ячейке кристалла.
54.
55.
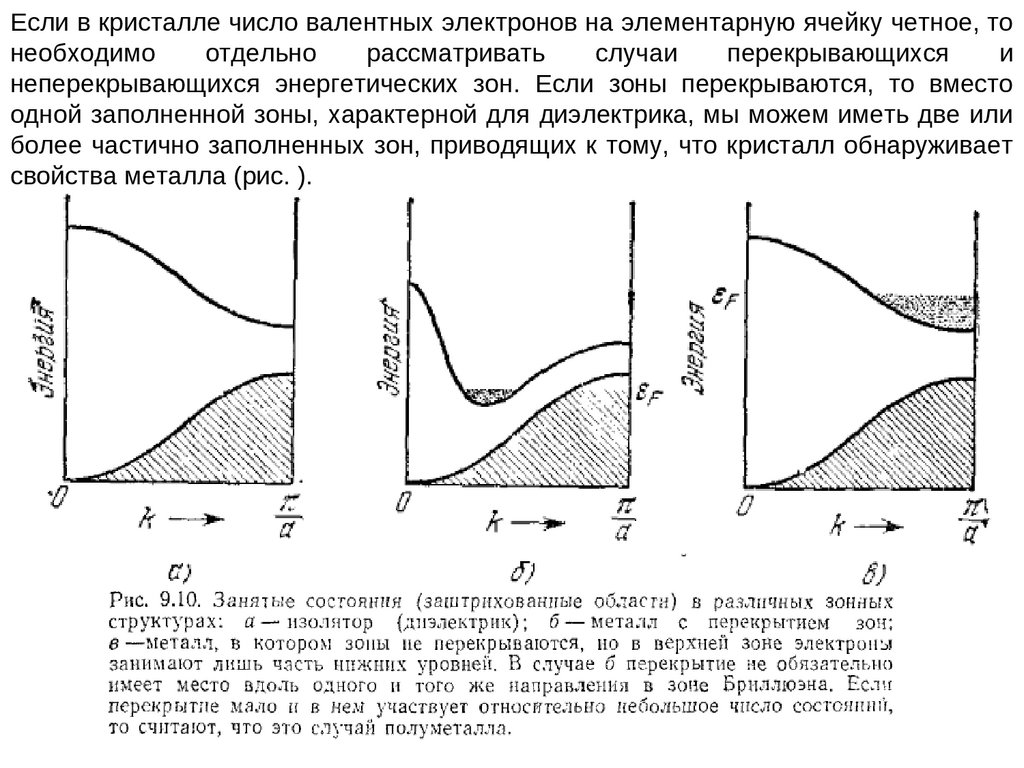
Если в кристалле число валентных электронов на элементарную ячейку четное, тонеобходимо
отдельно
рассматривать
случаи
перекрывающихся
и
неперекрывающихся энергетических зон. Если зоны перекрываются, то вместо
одной заполненной зоны, характерной для диэлектрика, мы можем иметь две или
более частично заполненных зон, приводящих к тому, что кристалл обнаруживает
свойства металла (рис. ).
56.
В щелочных и благородных металлах на элементарную ячейку приходитсяодин валентный электрон; и поэтому они являются металлами.
Редкоземельные металлы имеют по два валентных электрона на
элементарную ячейку и могли бы быть диэлектриками, но энергетические
зоны у них перекрываются, поэтому они металлы, хотя и не очень хорошие.
Кристаллы алмаза, кремния и германия имеют по два четырехвалентных
атома на элементарную ячейку. Энергетические зоны в них не
перекрываются, и поэтому чистые кристаллы при абсолютном нуле являются
диэлектриками.
Наивысшая из заполненных зон при абсолютном нуле называется валентной
зоной, наинизшая из незаполненных зон – зоной проводимости. Верхнюю
границу валентной зоны принято обозначать через , а нижнюю границу
зоны проводимости – через
; ширину запрещенной зоны
g
c
с
При g k BT
лишь немногие электроны получают в результате тепловой
флуктуации энергию достаточную для перехода его в зону проводимости
(диэлектрики).
При g ~ k BT
в зоне проводимости появляется заметное число
электронов, а в валентной зоне образуются свободные места – дырки.
В проводимости металла участвуют только электроны зоны проводимости,
имеющие энергию, близкую к энергии Ферми.
В полупроводниках в проводимости участвуют электроны обеих зон проводимости и валентной.
57.
При наличии малого числа свободных мест в валентной зоне обычно говорят нео движении многих электронов, а о движении свободных мест – дырок и
соответственно о дырочной проводимости в валентной зоне наряду с
электронной в зоне проводимости. Стремясь занять наинизшее энергетическое
состояние, электроны в зоне проводимости полупроводника располагаются
вблизи ее дна. Дырки в валентной зоне по той же причине сосредоточиваются
вблизи потолка валентной зоны.
Строение поверхности Ферми
Мы уже встречались с поверхностью Ферми, как поверхностью постоянной
энергии
F
в k– пространстве. Поверхность Ферми отделяет незаполненные
состояния (орбитали) от заполненных. При абсолютном нуле температур
большинство электронных свойств металлов определяется именно формой
поверхности Ферми.
Интерпретация поверхности
Ферми.
Формула Брэгга, определяющая границу
зон, имеет вид k 2 k 2 2k K KK ,
K 2k K
2
откуда следует
Эта формула удовлетворяется
значениями k оканчивающимися в плоскости,
нормальной к вектору K
и проходящими через его середину.
58.
Первая зона Бриллюэна квадратной решетки получается как область,заключенная между взаимно перпендикулярными прямыми,
проходящими
через середины кратчайших
векторов обратной решетки K1 и еще трех
векторов, эквивалентных K1 по симметрии (рис., а).
59.
Таким образом, первая зона Бриллюэна (элементарная ячейка Вигнера-Зейтцадля обратной решетки) это совокупность точек в k-пространстве, которых можно
достичь из начальной точки, не пересекая ни одной брэгговской плоскости. Для
построения первой зоны Бриллюэна нужны четыре вектора обратной решетки;
если постоянная решетки равна a, то эти четыре вектора суть
(2 / a)k x
и ( 2 / a)k y
Вторая зона Бриллюэна строится при помощи вектора K 2 и еще трех векторов,
эквивалентных по симметрии (рис. б). Аналогично строится третья зона. Числа 1,
2, 3 написаны на участках, относящихся к соответствующей по номеру зоне,
одновременно эти числа (в порядке возрастания) отвечают векторам обратной
решетки K , K , Kвозрастающей длины. Вторую зону Бриллюэна можно
определить так – совокупность точек, которых можно достичь из первой зоны, если
пересечь всего одну брэгговскую плоскость. Соответственно (n + 1) зону
Бриллюэна можно определить как совокупность точек, лежащих вне (n - 1) зоны,
которую можно достичь из n-зоны, пересекая всего лишь одну брэговскую
плоскость.
1
2
3
60.
Поверхность Ферми для свободных электроновПоверхность Ферми для свободных электронов при некоторой произвольной
концентрации электронов изображена на рис. 1 (случай плоской квадратной
решетки).
Рис. 1
рис. 2, а
рис. 2, б
рис. 2 в
Окружность описывает поверхность постоянной энергии для свободных
электронов. Ее площадь зависит только от концентрации электронов и не
зависит от взаимодействия с решеткой. Форма поверхности
зависит от
взаимодействия и не будет иметь форму окружности. Тот факт, что части
поверхности Ферми, относящиеся к одной зоне (например, второй) оказываются
отдаленными одна от друга, представляется неудобным. Это можно поправить,
перейдя к схеме приведенной зоны. Переместив треугольники, помеченные
цифрой 2 на вектор обратной решетки, они окажутся внутри первой зоны
Бриллюэна (рис. 2, б).
61.
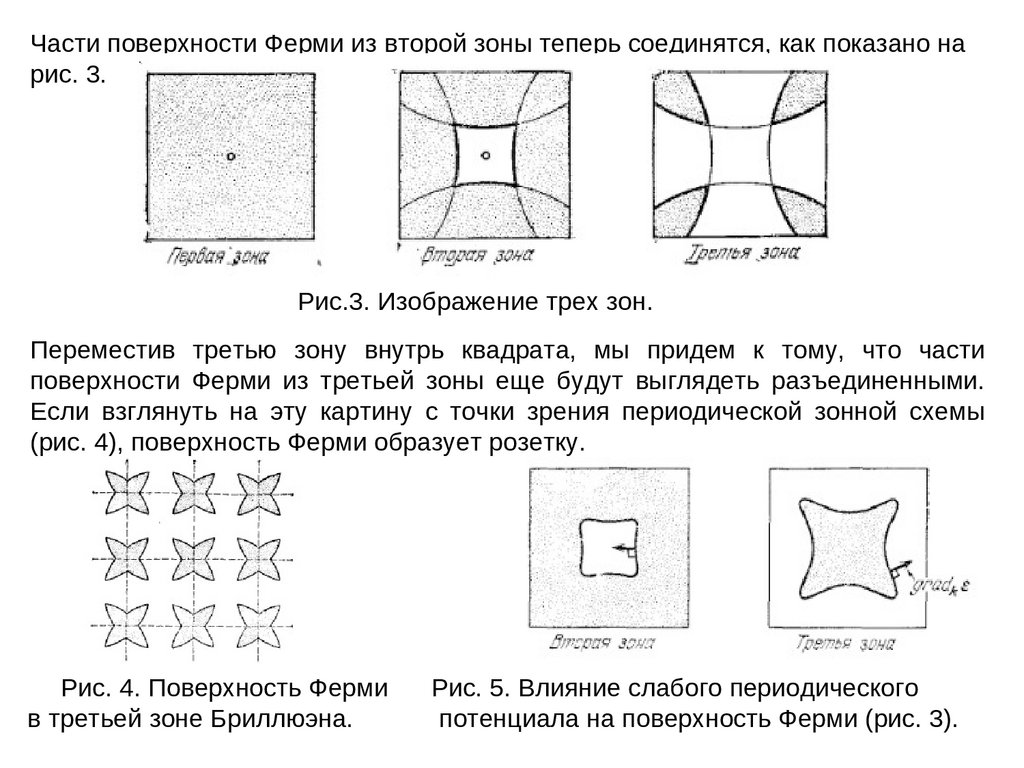
Части поверхности Ферми из второй зоны теперь соединятся, как показано нарис. 3.
Рис.3. Изображение трех зон.
Переместив третью зону внутрь квадрата, мы придем к тому, что части
поверхности Ферми из третьей зоны еще будут выглядеть разъединенными.
Если взглянуть на эту картину с точки зрения периодической зонной схемы
(рис. 4), поверхность Ферми образует розетку.
Рис. 4. Поверхность Ферми
в третьей зоне Бриллюэна.
Рис. 5. Влияние слабого периодического
потенциала на поверхность Ферми (рис. 3).
62.
Для перехода от поверхности Ферми для свободных электронов к поверхности дляпочти свободных электронов необходимо учесть следующие четыре факта:
а) Взаимодействие электрона с периодическим потенциалом кристалла приводит к
появлению энергетических щелей на зонных границах.
б) Почти вся поверхность Ферми будет пересекать границы зоны
перпендикулярно.
в) Внутрикристаллический потенциал будет особенно сказываться в «острых
углах» поверхности Ферми.
г) Полный объем, охватываемый поверхностью Ферми, зависит только от
концентрации электронов и не зависит от деталей их взаимодействия с решеткой.
Для количественных утверждений необходимы детальные расчеты, но можно
ожидать качественно, что поверхности Ферми, относящиеся ко второй и третьей
зонам Бриллюэна (рис.3.), под влиянием слабого внутрикристаллического поля
испытают изменения, характер которых можно усмотреть из рис. 5.
Приближенное построение поверхностей Ферми, исходя из поверхности для
свободных электронов, весьма полезно. Построение поверхности Ферми для
свободных электронов легко выполнить, пользуясь процедурой, предложенной
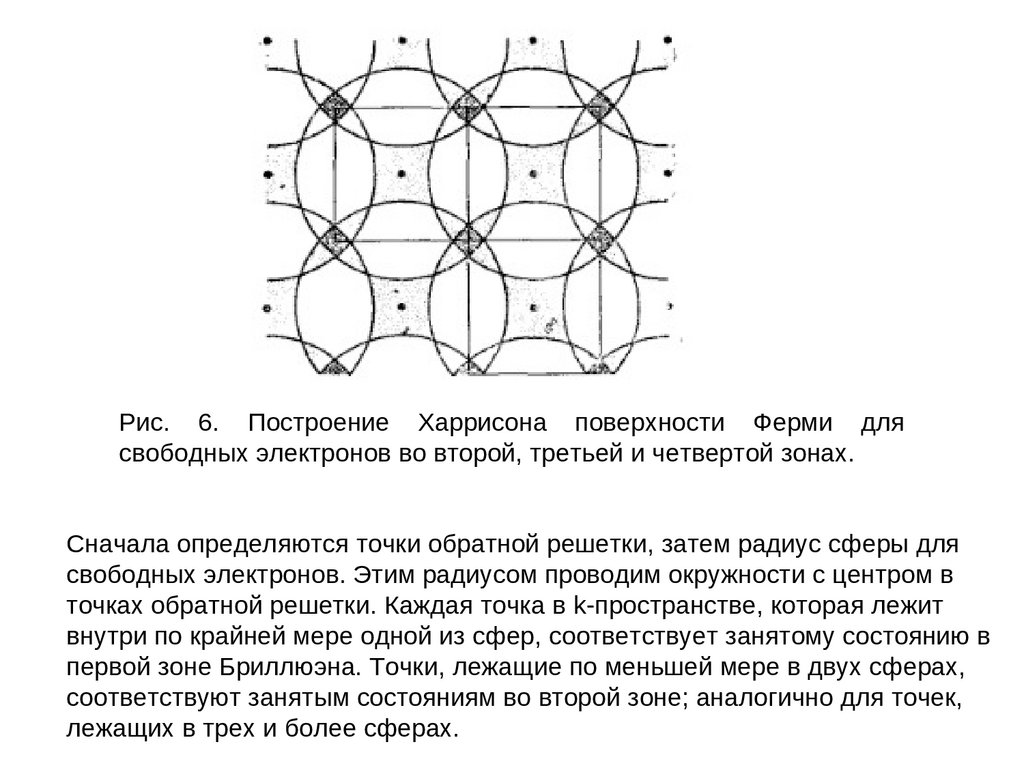
Харрисоном (рис. 6).
63.
Рис. 6. Построение Харрисона поверхности Ферми длясвободных электронов во второй, третьей и четвертой зонах.
Сначала определяются точки обратной решетки, затем радиус сферы для
свободных электронов. Этим радиусом проводим окружности с центром в
точках обратной решетки. Каждая точка в k-пространстве, которая лежит
внутри по крайней мере одной из сфер, соответствует занятому состоянию в
первой зоне Бриллюэна. Точки, лежащие по меньшей мере в двух сферах,
соответствуют занятым состояниям во второй зоне; аналогично для точек,
лежащих в трех и более сферах.























































 physics
physics








