Similar presentations:
Примеси и примесные состояния в полупроводниках
1. Твердотельная электроника
Электронный учебно-методическийкомплекс
Твердотельная электроника
Презентации к лекционному курсу
Примеси и примесные состояния
в полупроводниках
МОСКВА
2016
НИУ «МЭИ»
2.
• Для управления электрическимисвойствами полупроводников в них
специально вводят примеси
(легируют). Необходимо подчеркнуть,
что при замещении атома кристалл
остается электронейтральным!
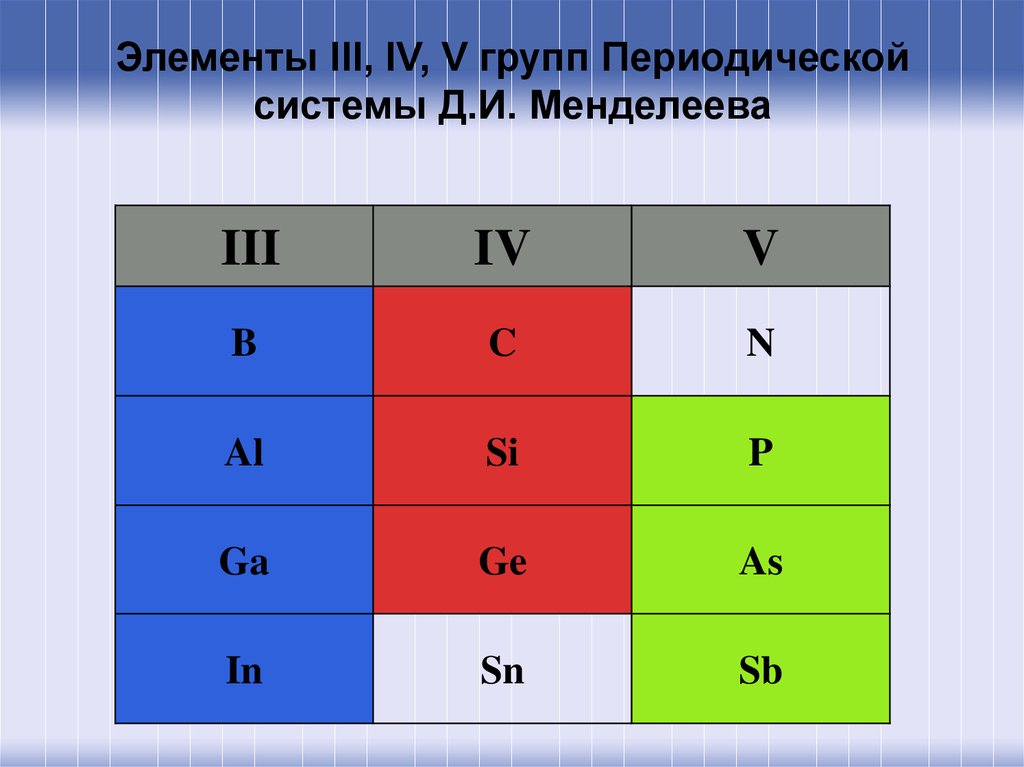
3. Элементы III, IV, V групп Периодической системы Д.И. Менделеева
IIIIV
V
B
C
N
Al
Si
P
Ga
Ge
As
In
Sn
Sb
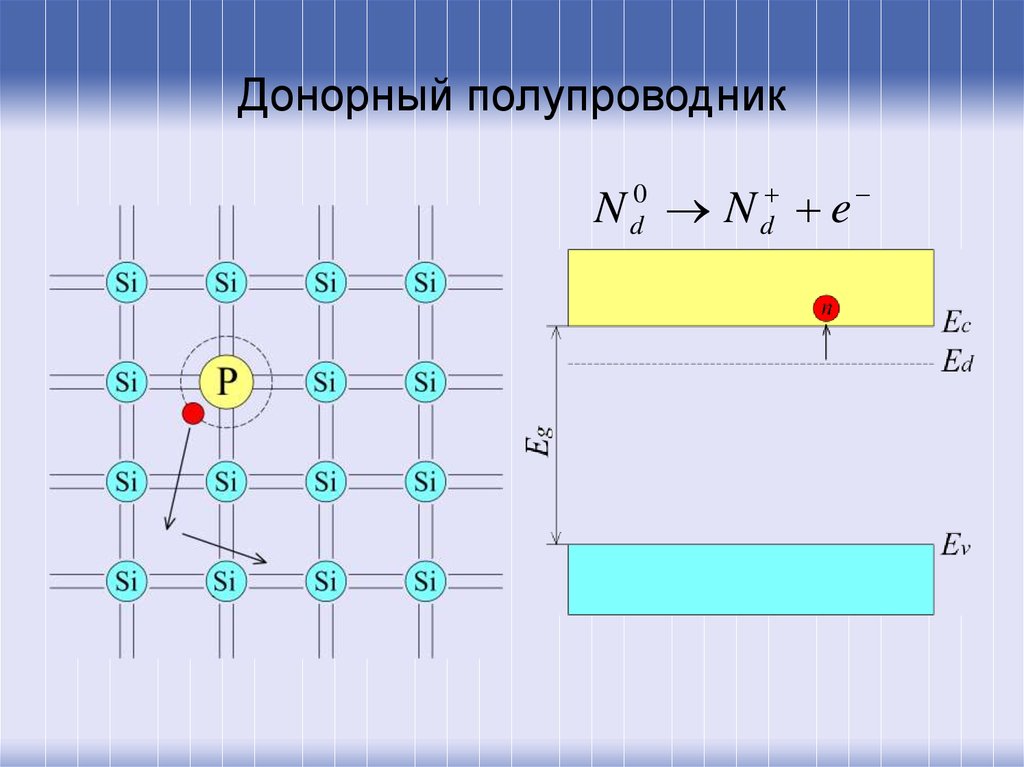
4. Донорный полупроводник
dN N e
0
d
5. Донорный полупроводник
• Энергия ионизации доноров (Ed), какправило, невелика и при комнатной
температуре донорная примесь отдает свои
электроны, поэтому такие полупроводники
и называют электронными или
полупроводниками n-типа, а электроны –
основными носителями заряда. Дырки в
электронном полупроводнике являются
неосновными носителями.
6. Уровень Ферми в донорном полупроводнике
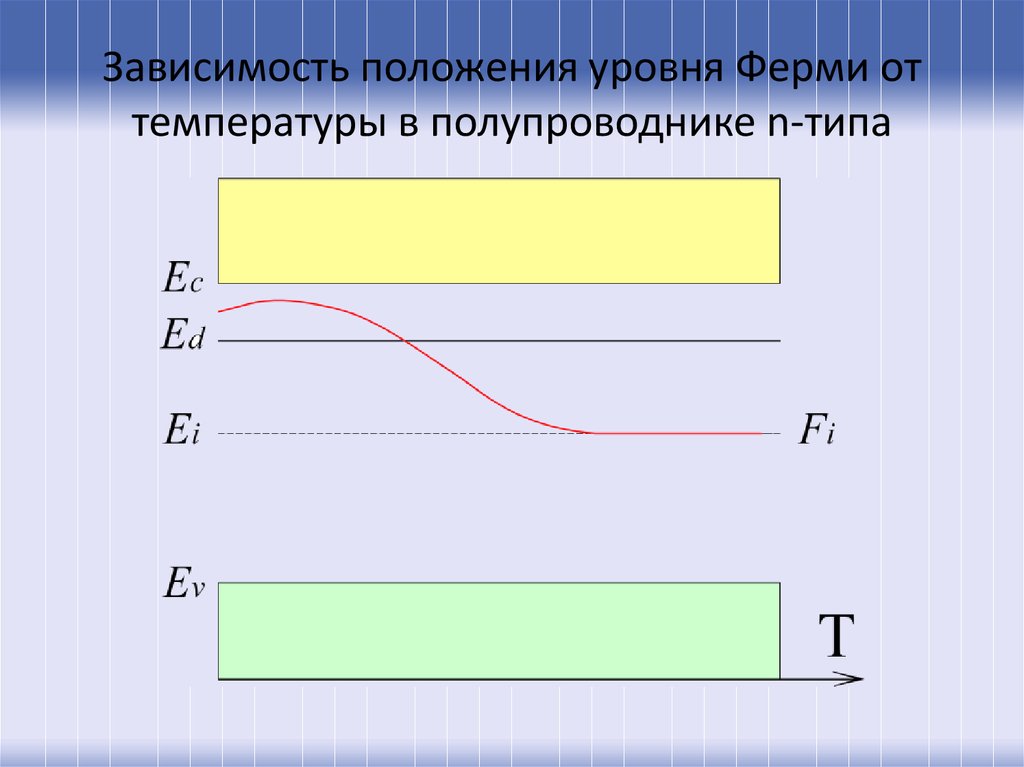
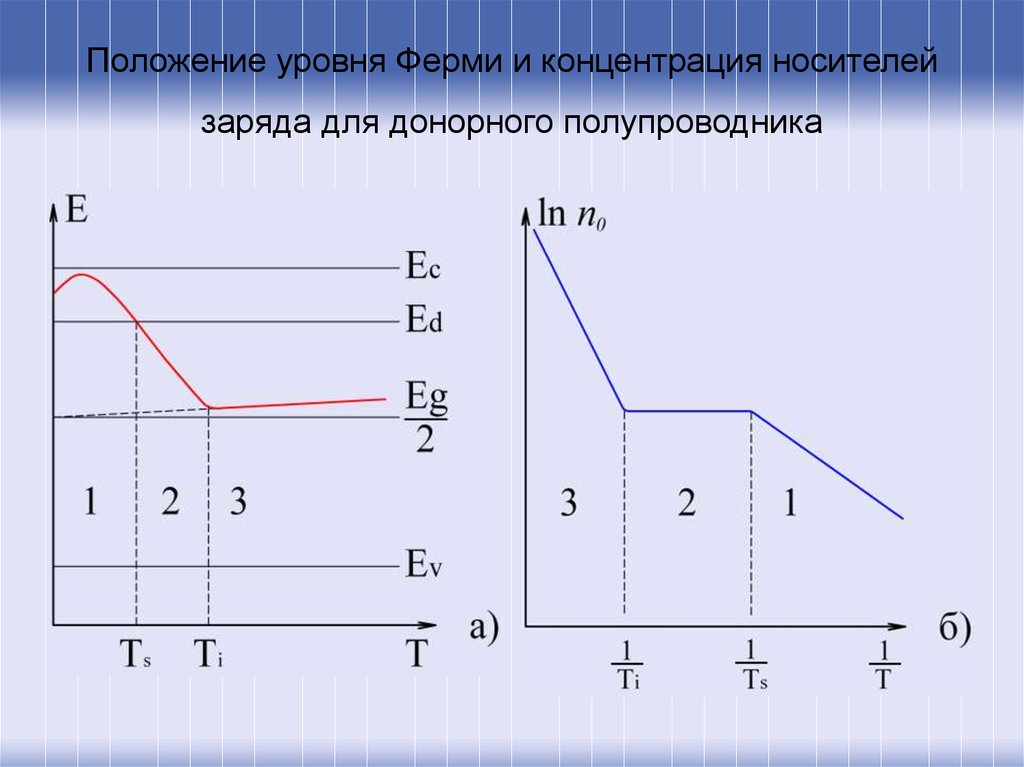
В невырожденном донорном полупроводнике при температуреабсолютного нуля уровень Ферми находится посередине между дном зоны
проводимости и уровнем донорной примеси. При повышении температуры
уровень Ферми стремится к середине запрещенной зоны
7. Донорный полупроводник
• Введение донорной примеси приводит кувеличению концентрации электронов (при
её ионизации) и, соответственно, к
смещению уровня Ферми к зоне
проводимости (чем он ближе к ней, тем
больше концентрация электронов).
8. Уравнение электронейтральности
Для собственного полупроводника:q n q p 0
n p
Если в полупроводнике присутствуют как донорная, так и
акцепторная примесь
q n q N
a
n Na p Nd
q p q N d 0
9.
В невырожденном донорном полупроводнике притемпературе абсолютного нуля уровень Ферми
находится посередине между дном зоны проводимости и
уровнем донорной примеси. При повышении
температуры уровень Ферми стремится к середине
запрещенной зоны
;
nd
10. Зависимость положения уровня Ферми от температуры в полупроводнике n-типа
11. Заполнение электронами зоны проводимости в невырожденном полупроводнике n-типа
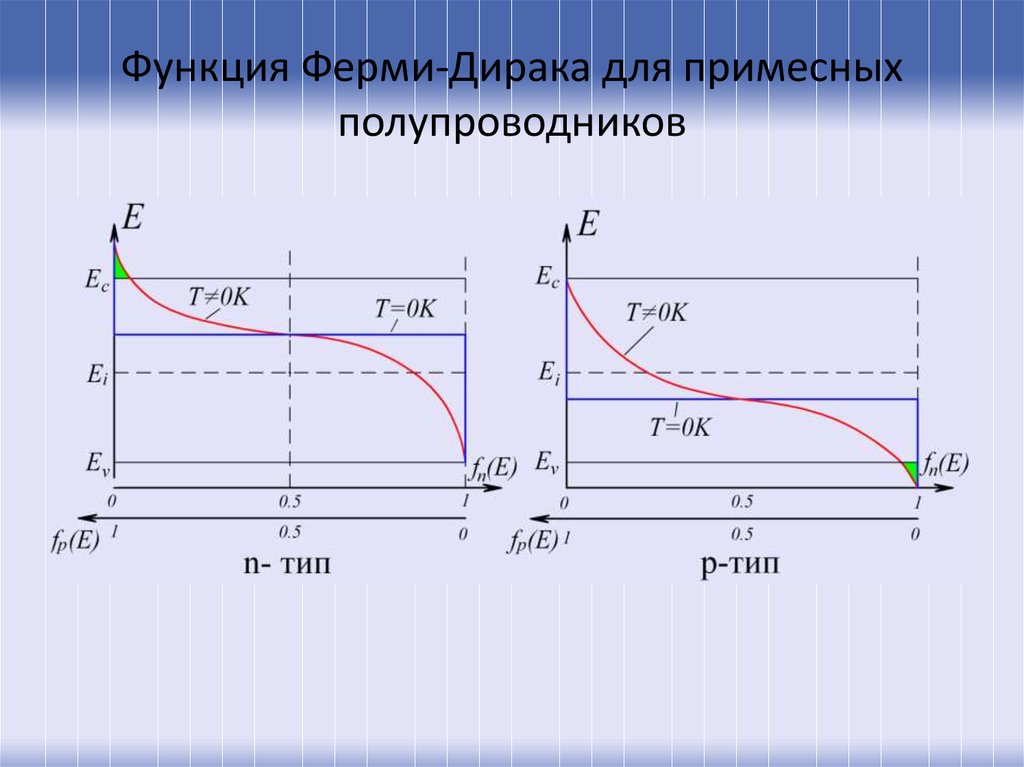
12. Функция Ферми-Дирака для примесных полупроводников
13. Положение уровня Ферми и концентрация носителей заряда для донорного полупроводника
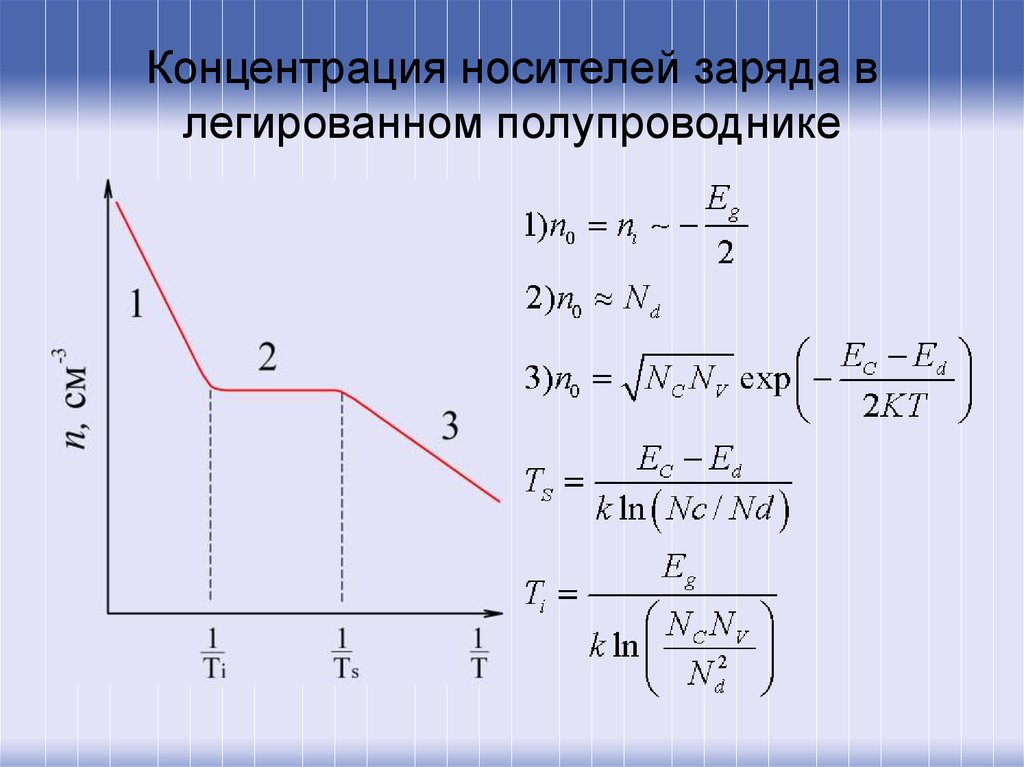
14. Концентрация носителей заряда в легированном полупроводнике
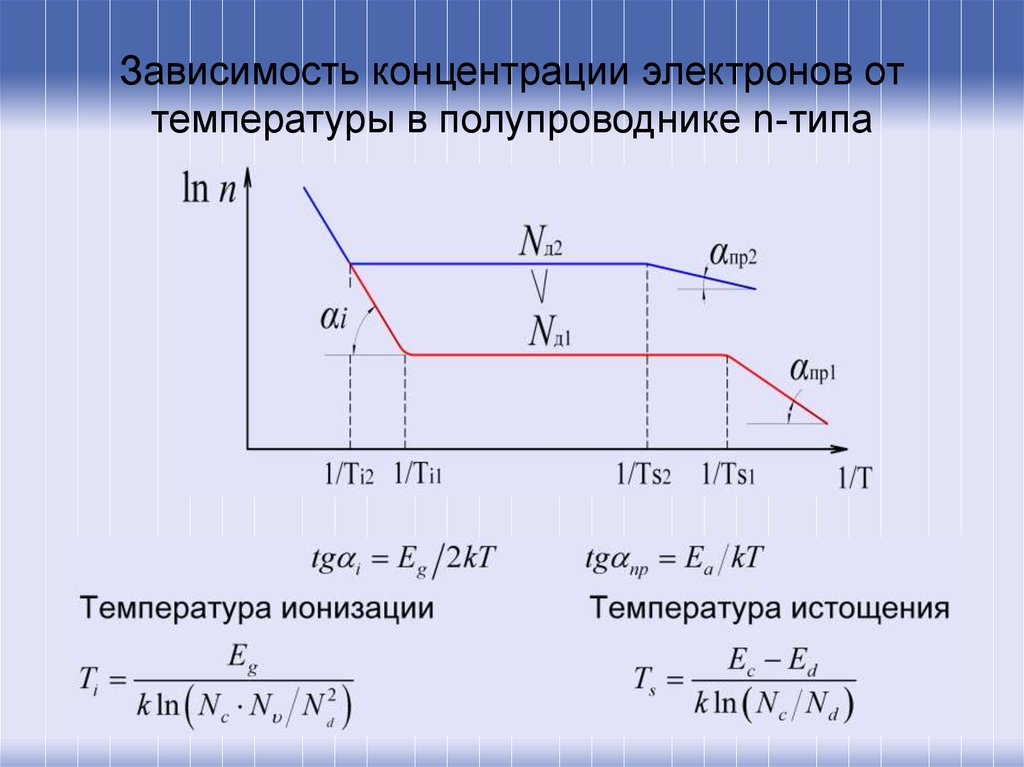
15. Зависимость концентрации электронов от температуры в полупроводнике n-типа
16.
В области температур между Ti и Ts (при температурах,близких к комнатной) можно легко рассчитать концентрацию
неосновных носителей заряда
ni n0 p0
2
ni2
ni2
pn , nn N d , pn
nn
Nd
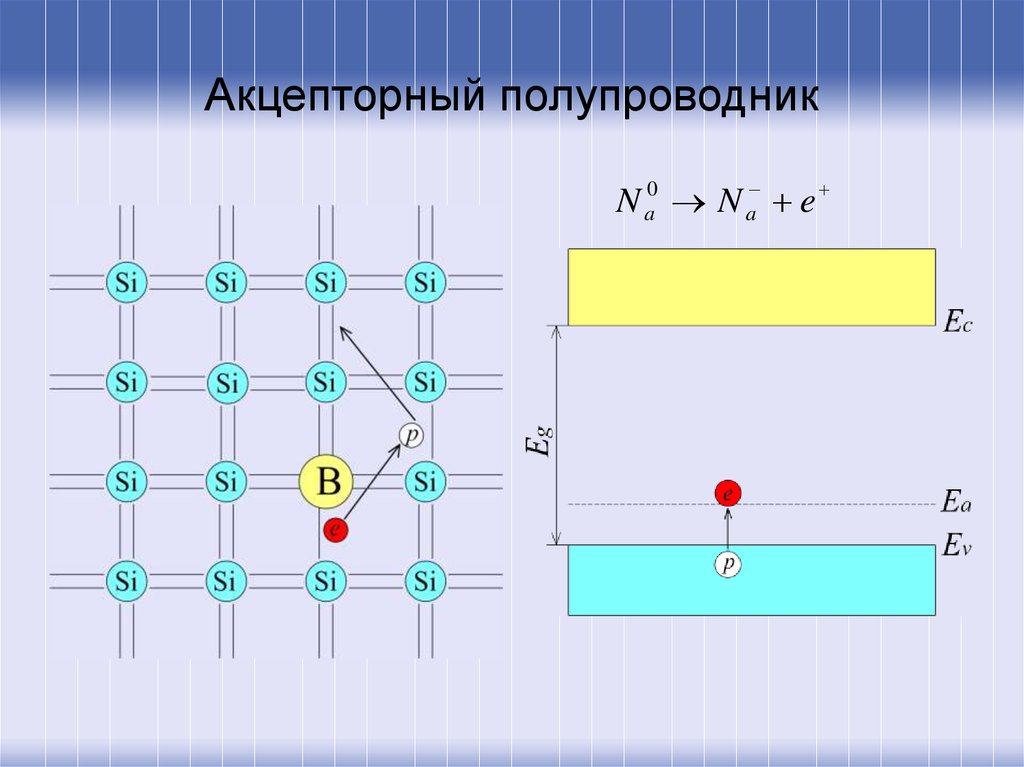
17. Акцепторный полупроводник
N a0 N a e18. Акцепторный полупроводник
• Энергия ионизации акцепторов Ea<<Eg, ипри комнатной температуре акцепторная
примесь ионизованна, поэтому такие
полупроводники и называют
полупроводниками p-типа, а дырки –
основными носителями заряда.
Электроны в полупроводнике p-типа
являются неосновными носителями.
Введение акцепторной примеси приводит к
смещению уровня Ферми к валентной зоне.
19. Уровень Ферми в акцепторном полупроводнике
(6.3)(6.4)
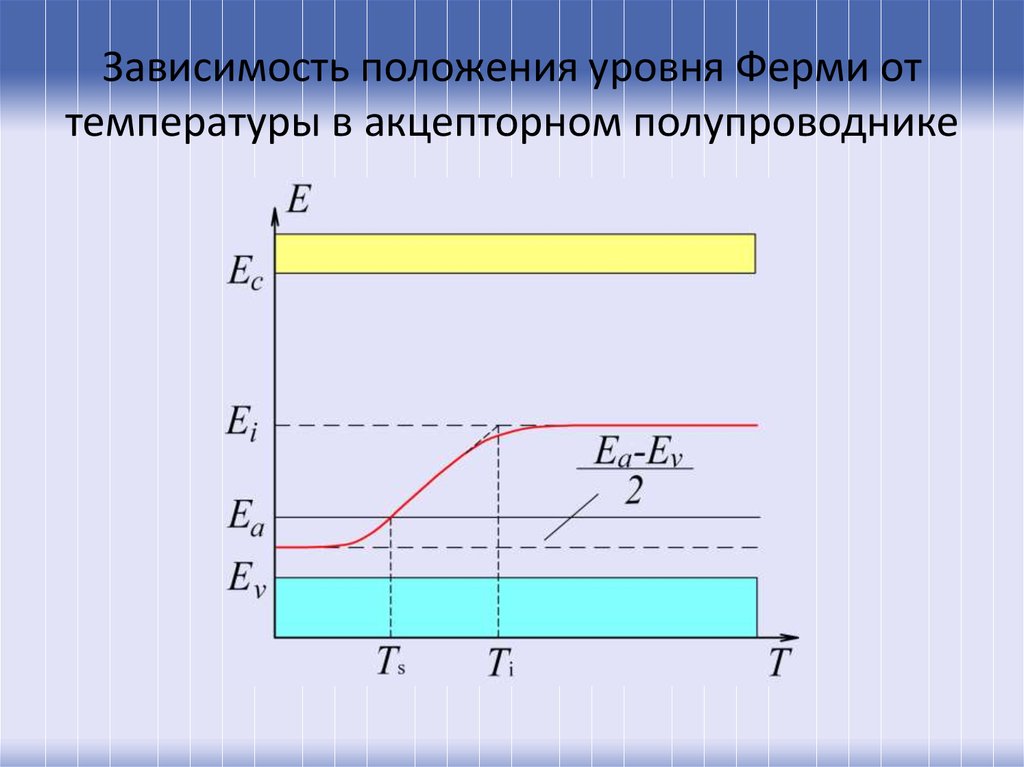
20. Зависимость положения уровня Ферми от температуры в акцепторном полупроводнике
21.
pp Napn n
2
i
Nd
np n Na
2
i
22. Зависимость положения уровня Ферми от температуры для Ge n- и p-типов
23. Уравнение электронейтральности
Для собственного полупроводника:q n q p 0
n p
Если в полупроводнике присутствуют как донорная, так и
акцепторная примесь
q n q N
a
n Na p Nd
q p q N d 0
24.
Проводимость полупроводниковЭлектронная проводимость
25.
Средняя тепловая скорость движения электронов будетопределяться классическим соотношением:
2
T
m v
3
kT
2
2
*
n
vT
~107 см/с – средняя тепловая скорость
электронов, k – постоянная Больцмана
26.
Электроны взаимодействуют с дефектами кристаллическойрешетки, между собой и ядрами, изменяя (рассеивая) свою
кинетическую энергию.
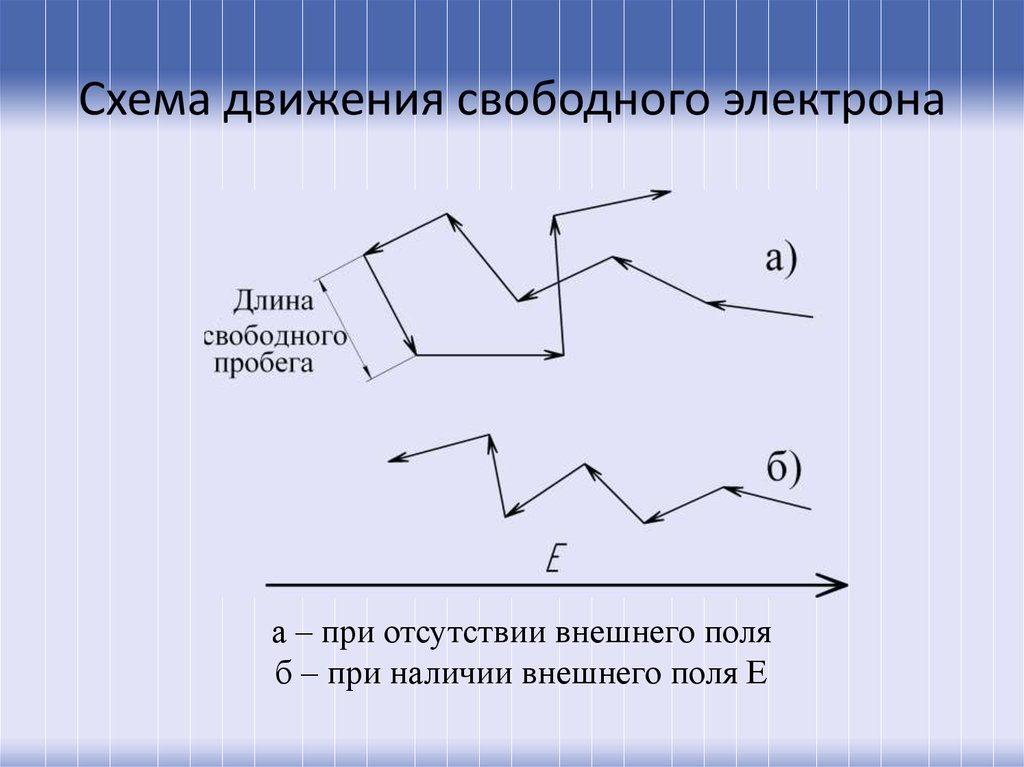
Усредненное значение участков пути, пройденное электроном
между актами рассеяния, называются средней длиной свободного
пробега. Время между двумя актами взаимодействия – временем
свободного пробега: l св v T
При воздействии электрического поля Ē на полупроводник
средняя скорость движения носителей заряда становится не равной
нулю ( v 0 ) в направлении, определяемом направлением
напряженности электрического поля, она называется дрейфовой
скоростью. Движение носителей заряда под воздействием
электрического поля называется дрейфом
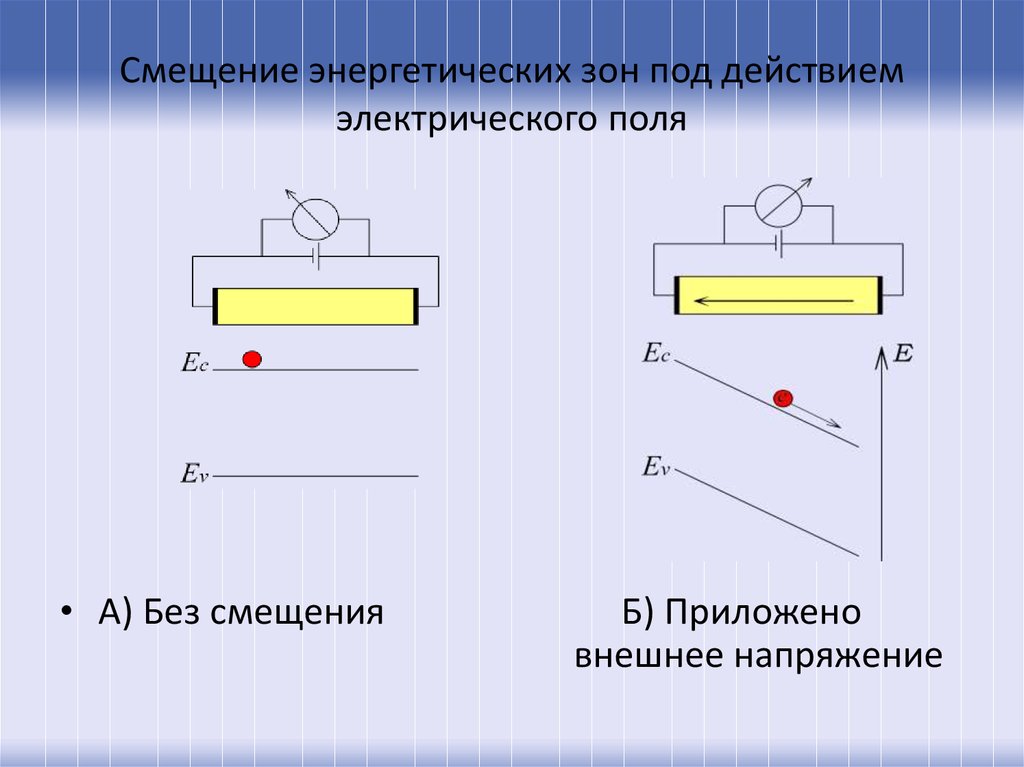
27. Смещение энергетических зон под действием электрического поля
• А) Без смещенияБ) Приложено
внешнее напряжение
28.
29. Расчет скорости свободного электрона
30. Схема движения свободного электрона
а – при отсутствии внешнего поляб – при наличии внешнего поля Е
31.
Коэффициент пропорциональности между дрейфовойскоростью и напряженностью электрического поля называют
подвижностью носителей заряда и обозначают μ [см 2 /В с ]
vдр q
n
*
E
mn
.
Предположим, что ток через образец создается
электронами, концентрация которых n и средняя дрейфовая
скорость v
др
32.
Поскольку величина тока равна заряду, проходящемучерез сечение образца в единицу времени, плотность тока
при слабом электрическом поле по закону Ома:
I U R J S ,
U E l,
1
где σ – проводимость.
R l S ,
j n q vдр
33.
Отсюда легко получить закон Ома в дифференциальнойформе:
Jn n E
Где
n – электронная проводимость (Ом∙см)
n q n n
Проводимость
материала
определяется
двумя
основными параметрами: подвижностью носителей
заряда и их концентрацией.
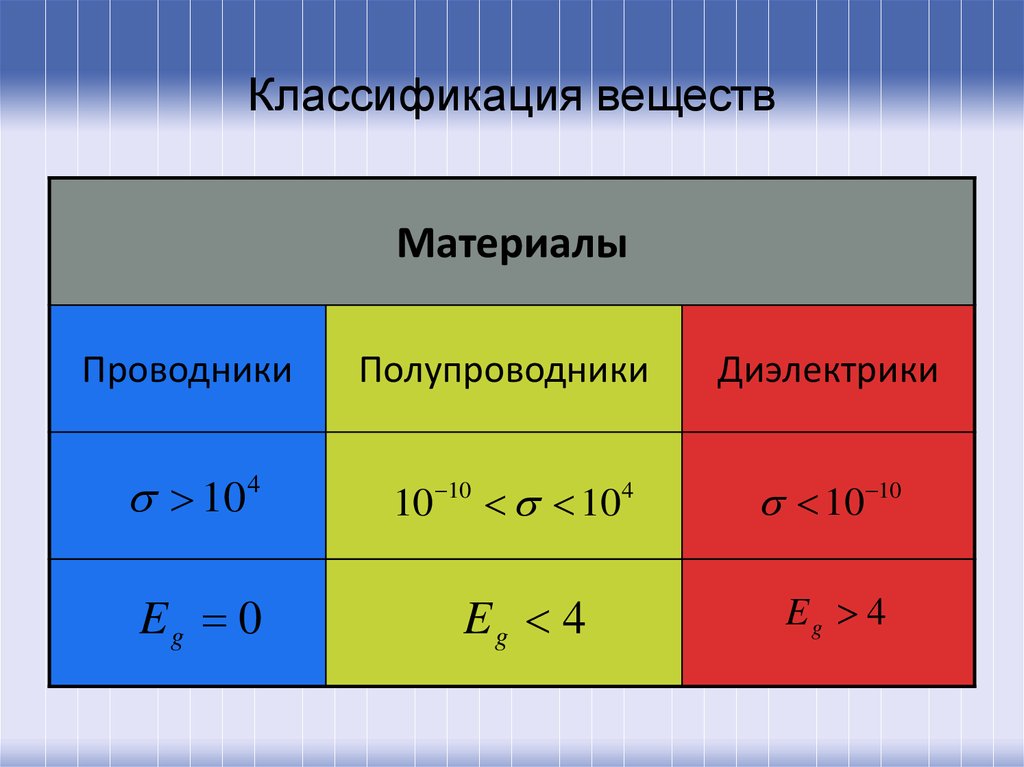
34. Классификация веществ
МатериалыПроводники
Полупроводники
Диэлектрики
104
10 10 104
10 10
Eg 0
Eg 4
Eg 4
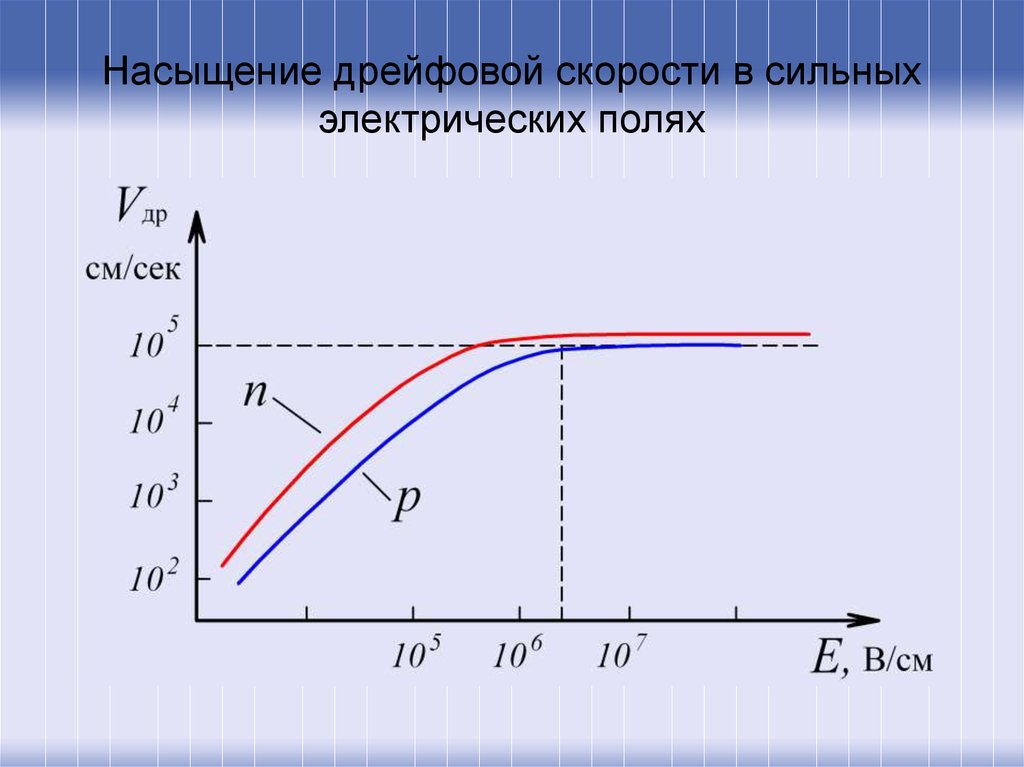
35. Насыщение дрейфовой скорости в сильных электрических полях
36.
Существует несколько механизмов рассеяния энергиисвободных носителей заряда. Для полупроводников наиболее
важные два: рассеяние в результате взаимодействия с
колебаниями решетки (решеточное рассеяние) и рассеяние в
результате взаимодействия с ионизованной примесью.
Рассеяние – мгновенные события, внезапно меняющие
скорость электронов. По теории Друде (1900 г.) рассеяние на
самих электронах не является важным! Экспериментальные
исследования температурной зависимости подвижности
показывают, что при низких температурах преобладает
рассеяние на ионах примеси, а при более высоких – рассеяние
на тепловых колебаниях решетки.
37. Подвижность носителей заряда
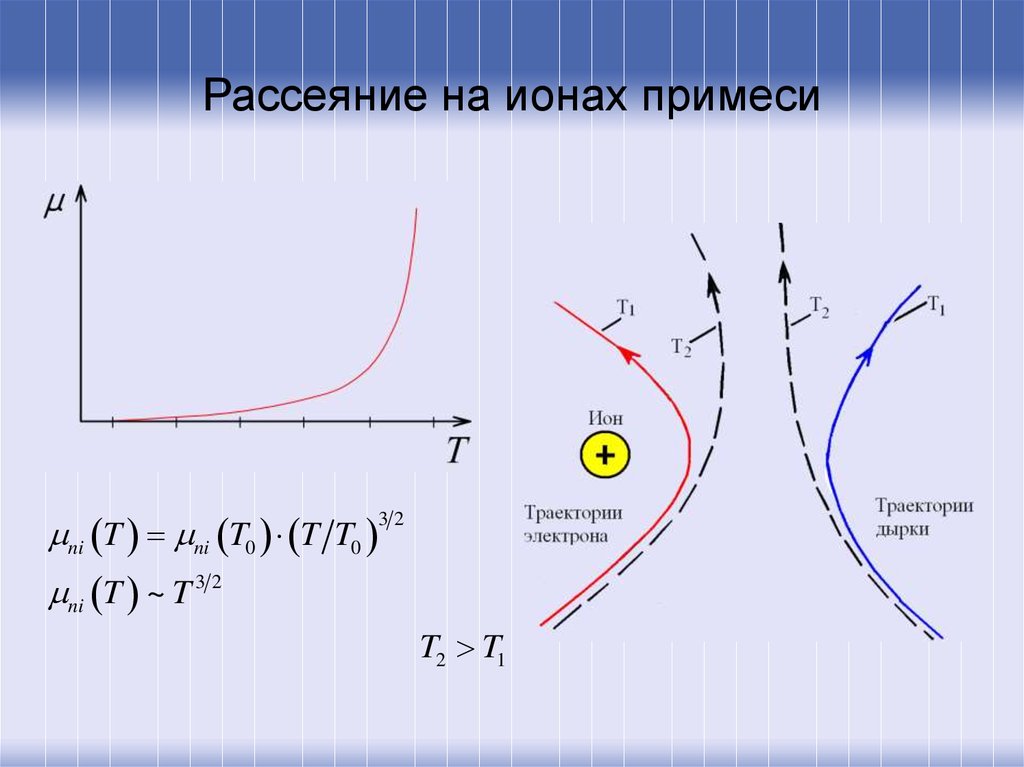
38. Рассеяние на ионах примеси
ni T ni T0 T T032
ni T ~ T 3 2
T2 T1
39.
Подобно тому, как электромагнитное поле излученияможно трактовать как набор световых квантов – фотонов, поле
упругих колебаний, заполняющих кристалл, можно считать
совокупностью квантов нормальных колебаний решетки –
фононов.
Фонон (термин введен И.Е. Таммом) – квант колебаний
атомов кристаллической решетки.
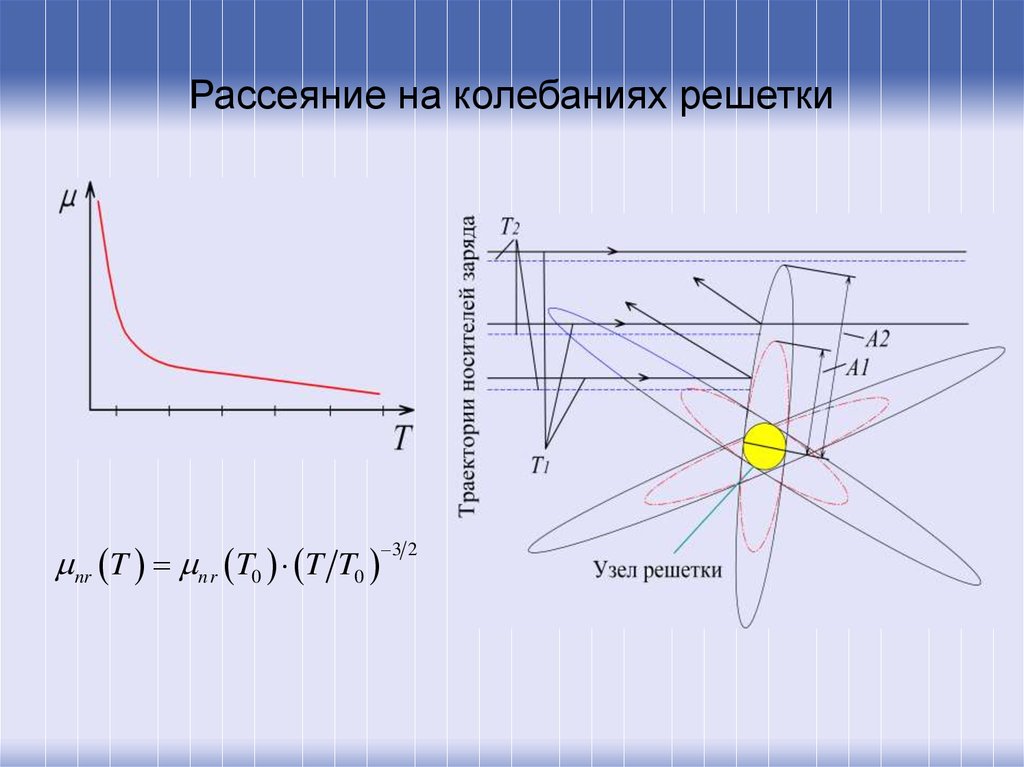
40. Рассеяние на колебаниях решетки
nr T nr T0 T T03 2
41.
При одновременном действии нескольких механизмоврассеяния для расчета подвижности можно воспользоваться
понятием эффективной подвижности носителей.
1
eff
eff
1
1
r i
r i
,
r i
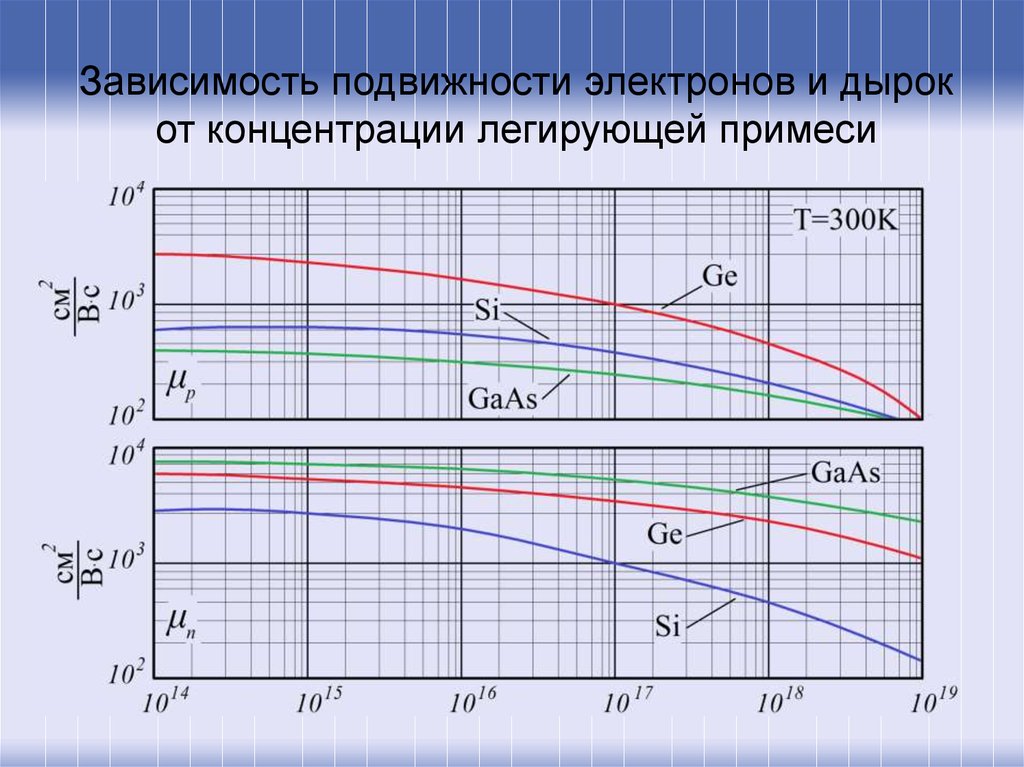
42. Зависимость подвижности электронов и дырок от концентрации легирующей примеси
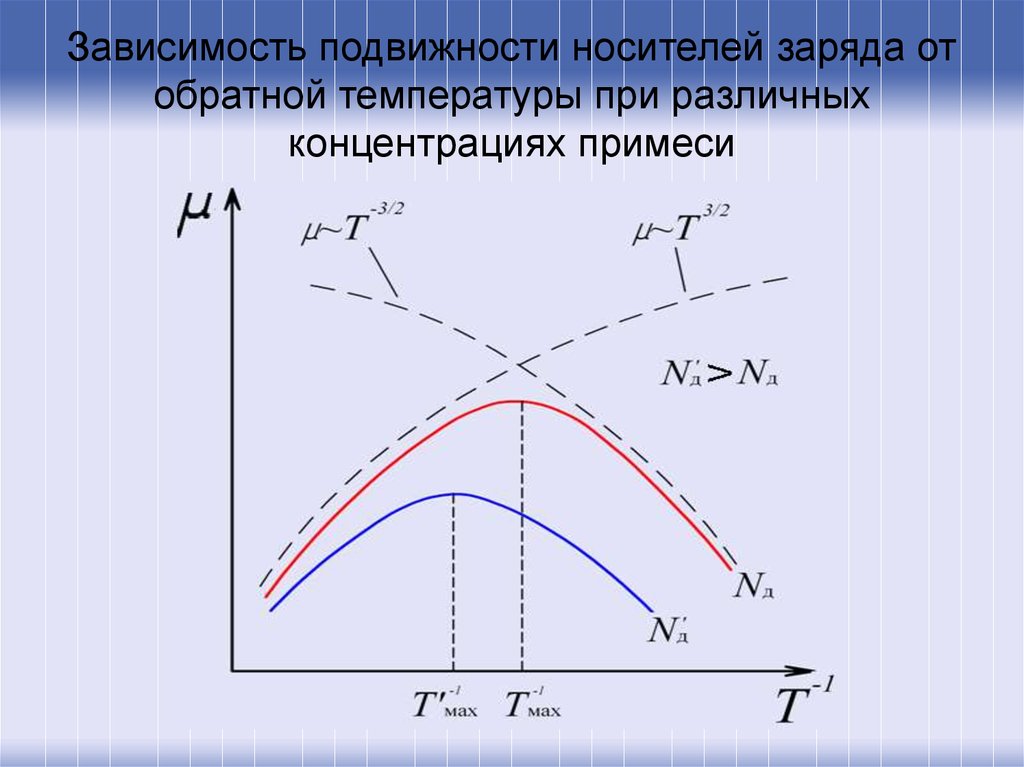
43. Зависимость подвижности носителей заряда от обратной температуры при различных концентрациях примеси
44.
Поскольку в собственном полупроводнике отсутствуютпримеси, рассеяние электронов и дырок в нем должно
происходить только на тепловых колебаниях решетки, т.е. в
собственных кристаллах значение подвижности носителей
заряда должно быть максимальным
45. Типичные значения подвижности (300К) для некоторых полупроводников
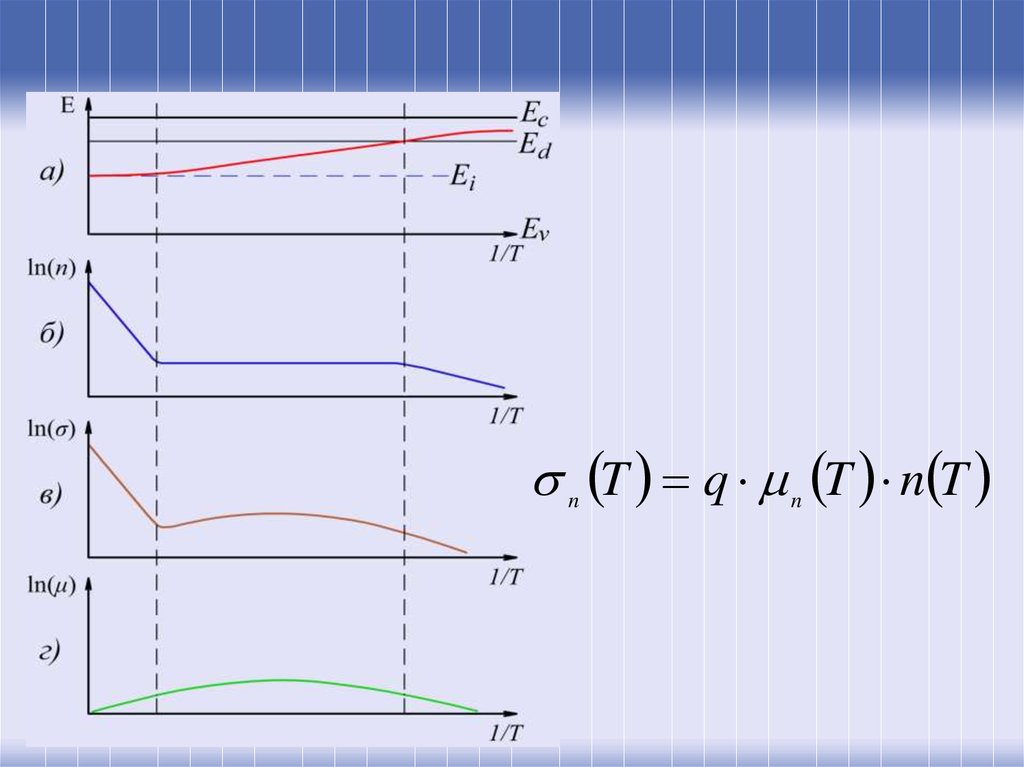
46.
n T q n T n T47.
Дырочная проводимостьq vдр
p *
mp
p q p p
j p p .
Чем больше подвижность, тем больше дрейфовая
скорость носителей заряда и тем выше быстродействие
полупроводникового прибора
pr T p r T0 T T0
3 2
pi T pi T0 T T0
32
48. Расчет электропроводности
49.
Суммарная электропроводность материала определяетсяобщим количеством электронов и дырок:
n p q n n q p p q n n p p
Плотность тока в кристалле будет равна
J J n J p E n p E q n n p p E
50. Собственная проводимость
Зависимостьэлектропроводности
материала от температуры:
собственного
σi (T ) q n (T ) n(T ) q p (T ) p(T ) q [ n (T ) p (T )] ni (T )
* *
2 mn m p kT
σ (T ) 2q
i
2
h
Eg Т
exp
0
2kT
3/ 2
Eg Т
(T ) (T ) exp
p
2kT
n
51.
По экспериментальной зависимости электропроводностиот температуры можно оценить ширину запрещенной зоны
E
E
g
g
(T1) 0 (T1) exp
0 exp
,
2kT
2kT
1
1
E
g
(T2 ) 0 (T2 ) exp
2kT
2
E
g
exp
0
2kT
2
(T )
1
Eg 2k ln
(T )
2
,
1
1
T
T
1
2











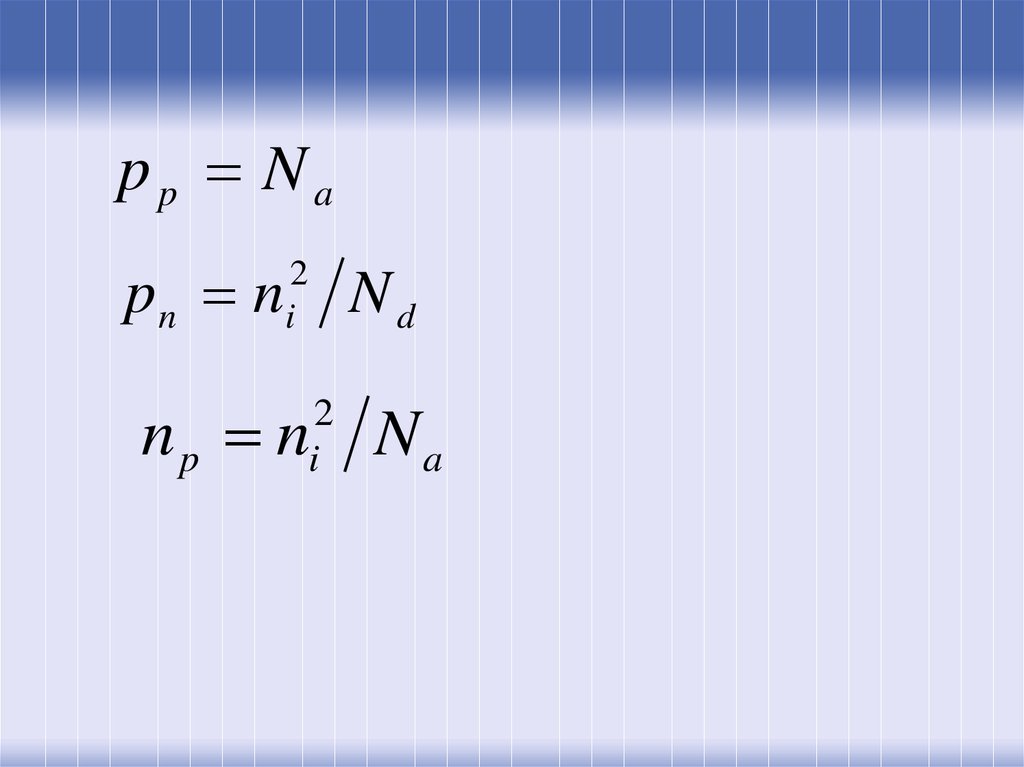




















 physics
physics








