Similar presentations:
Виды движения
1. Кинематика – раздел механики, в котором изучают движение материальных тел без учета причин, его вызывающих
Виды движения:–
–
–
–
–
Основные задачи
Поступательное
кинематики:
Вращательное
– Установление
Плоскопараллельное
математических
Сферическое
способов задания
Сложное
движения точек (тел)
Кинематические
характеристики:
– Положение точки
(тела)
– Траектория
– Скорость
– Ускорение
– Зная закон движения
точки (тела), установить
методы определения
всех величин,
характеризующих данное
движение
2. Глава 1 Кинематика точки
§ 1. Способы задания движения§ 2. Скорость и ускорение точки
2.1. Скорость при векторном способе задания
движения точки
2.2. Ускорение при векторном способе задания
движения точки
2.3. Скорость при координатном способе задания
движения точки
2.4. Ускорение при координатном способе задания
движения точки
2.5. Скорость при естественном способе задания
движения точки
2.6. Ускорение при естественном способе задания
движения точки
§ 3. Частные случаи движения точки
3.
§ 1. Способы задания движенияДвижение точки по отношению к
избранной системе отсчета считается
заданным, если известен способ, при
помощи которого можно определить
положение точки в любой момент
времени
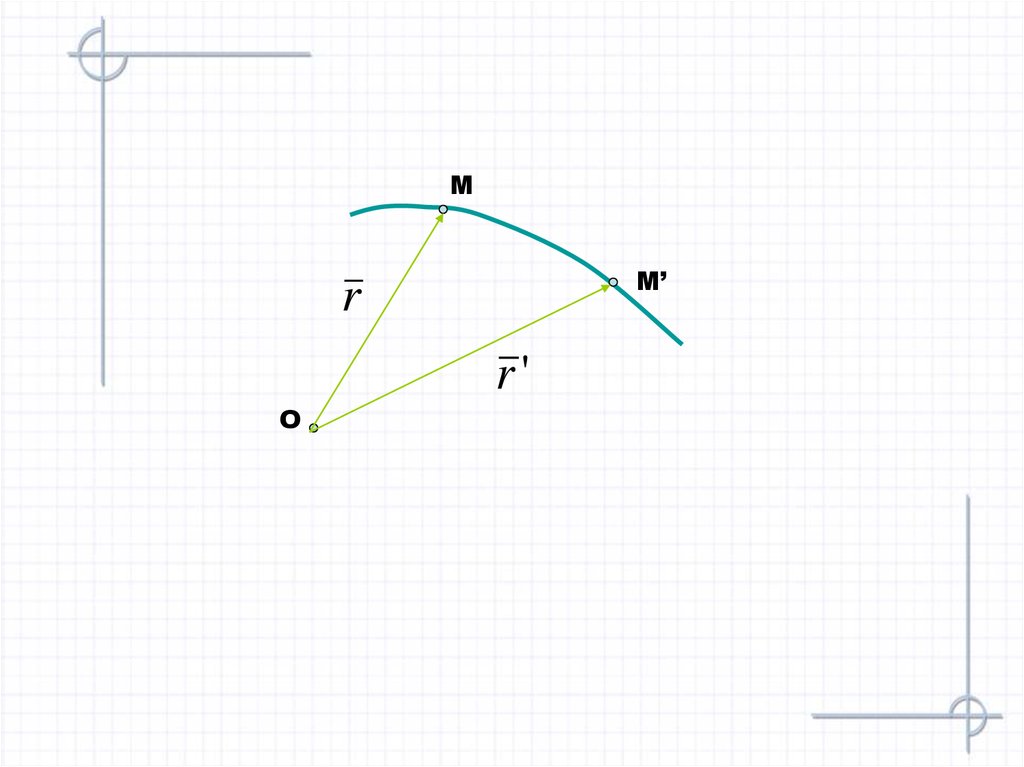
Точка, двигаясь в пространстве, описывает
кривую, называемую траекторией
4.
ММ’
r
r'
O
5. Способы задания движения
Векторный способ задания движенияr r t
6.
ZМ
z’
М’
r
r'
k
j
O
x’
X
i
y’
Y
7. Способы задания движения
Векторный способ задания движенияКоординатный способ задания
движения
r r t
x x t
y y t
z z t
8.
Естественный (траекторный) способзадания движения
+
-
М
задаем траекторию
s (t)
O
М’
движения
начало отсчета
направление отсчета
расстояний
закон движения точки
по траектории s = s(t)
9. Способы задания движения
Векторный способ задания движенияКоординатный способ задания
движения
Естественный (траекторный) способ
задания движения
r r t
x x t
y y t
z z t
s s t
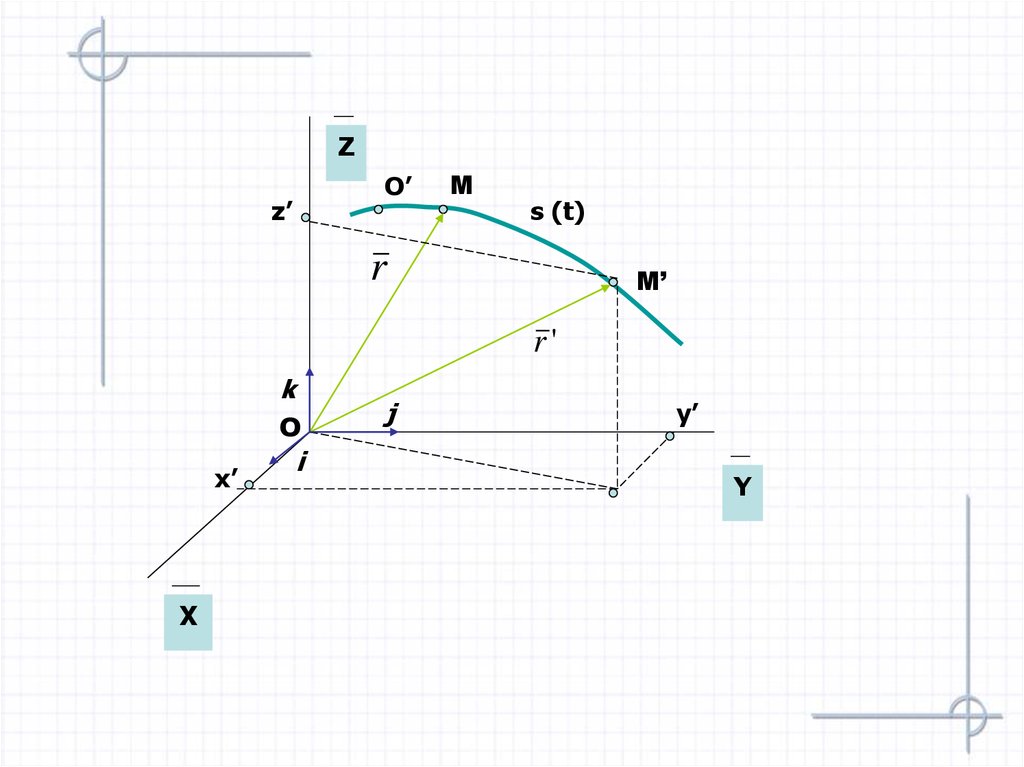
10.
ZO’
z’
М
s (t)
r
М’
r'
k
O
x’
X
i
j
y’
Y
11.
СкоростьСкорость точки
V (векторная величина) одна из
основных кинематических характеристик движения
точки
Под средней скоростью точки (по модулю и
направлению) понимают величину, равную отношению
вектора перемещения к промежутку времени, за
который это перемещение произошло
Vcp
MM 1
t
Скорость точки в данный момент времени называется
мгновенной скоростью точки
MM 1
V lim
t 0 t
12.
2.1. Скорость при векторном способезадания движения точки
М
В момент времени t
r
r r t
при t1= t + ∆t
М1
r
r1 r t t
O
Vcp
MM 1 r
;
t
t
r1 r t t
r1 r t t r MM1
MM1 r1 r r
.
r dr
V lim
r
t 0 t
dt
длина м км
V время с ; час
13. 2.2. Ускорение при векторном способе задания движения точки
МВ момент времени t
скорость точки М V V t
при t1= t + ∆t в точке М1
V1 V1 t1 V t t
V r
aср
М1
V
V1
V V1 V V t t V t
V
O
acp
V
;
t
V
dV d 2 r
r
a lim
V
t 0 t
dt
dt 2
длина
м
a
2
2
время
с
14.
2.3. Скорость при координатном способезадания движения точки
М
r
r
O
V
V
М1
r1 r t t
k
j
i
r xi y j zk
r r1 r MM1
dr dx
dy
dz
i
j k
dt dt
dt
dt
V x i y j z k
V Vx i V y j Vz k
V V Vx2 V y2 Vz2
Vx
cos V , x
V
Vy
cos V, y
V
Vz
cos V , z
V
направляющ ие
косинусы
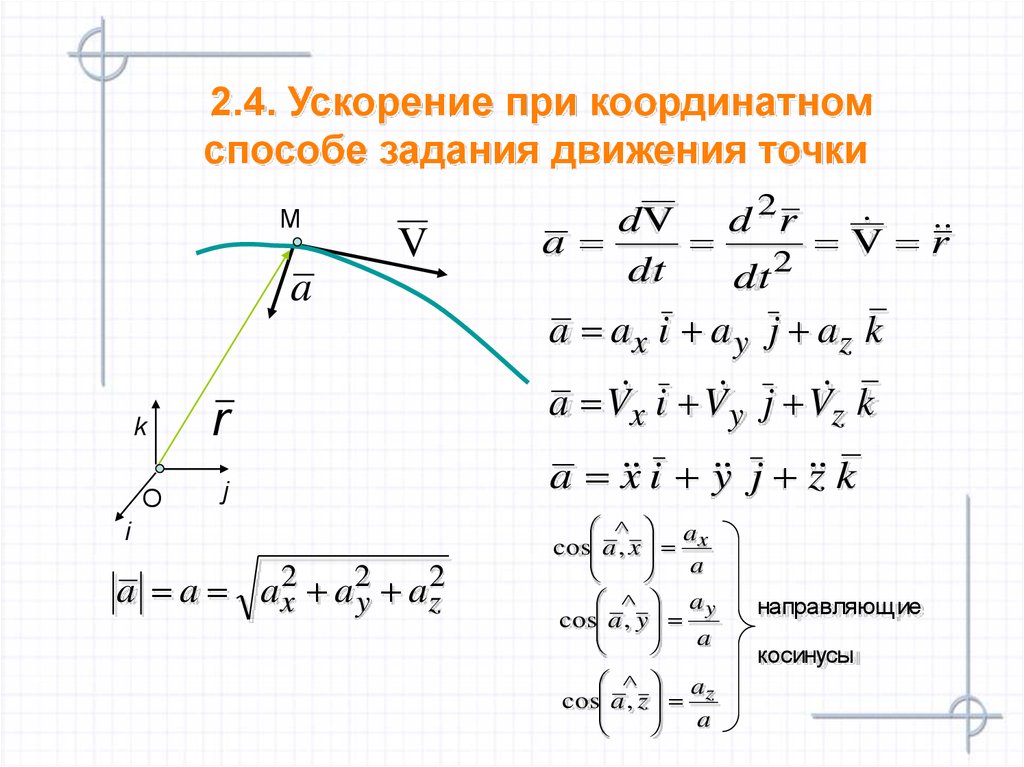
15. 2.4. Ускорение при координатном способе задания движения точки
МV
a
k
O
r
j
i
a a ax2 a 2y az2
dV d 2 r
r
a
V
dt
dt 2
a ax i a y j az k
a V x i V y j V z k
a x i y j z k
ax
cos a , x
a
ay
cos a , y
a
az
cos a , z
a
направляющ ие
косинусы
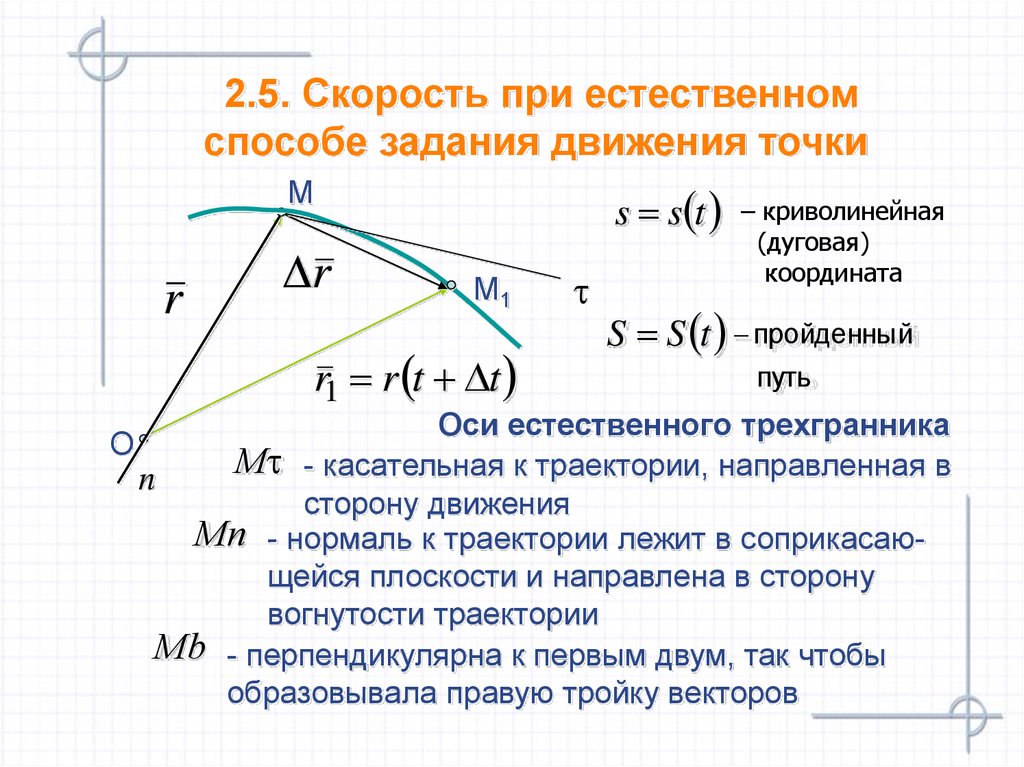
16. 2.5. Скорость при естественном способе задания движения точки
Мr
s s t
r
М1
r1 r t t
O
– криволинейная
(дуговая)
координата
S S t пройденный
путь
Оси естественного трехгранника
М - касательная к траектории, направленная в
n
сторону движения
Мn - нормаль к траектории лежит в соприкасающейся плоскости и направлена в сторону
вогнутости траектории
Мb - перпендикулярна к первым двум, так чтобы
образовывала правую тройку векторов
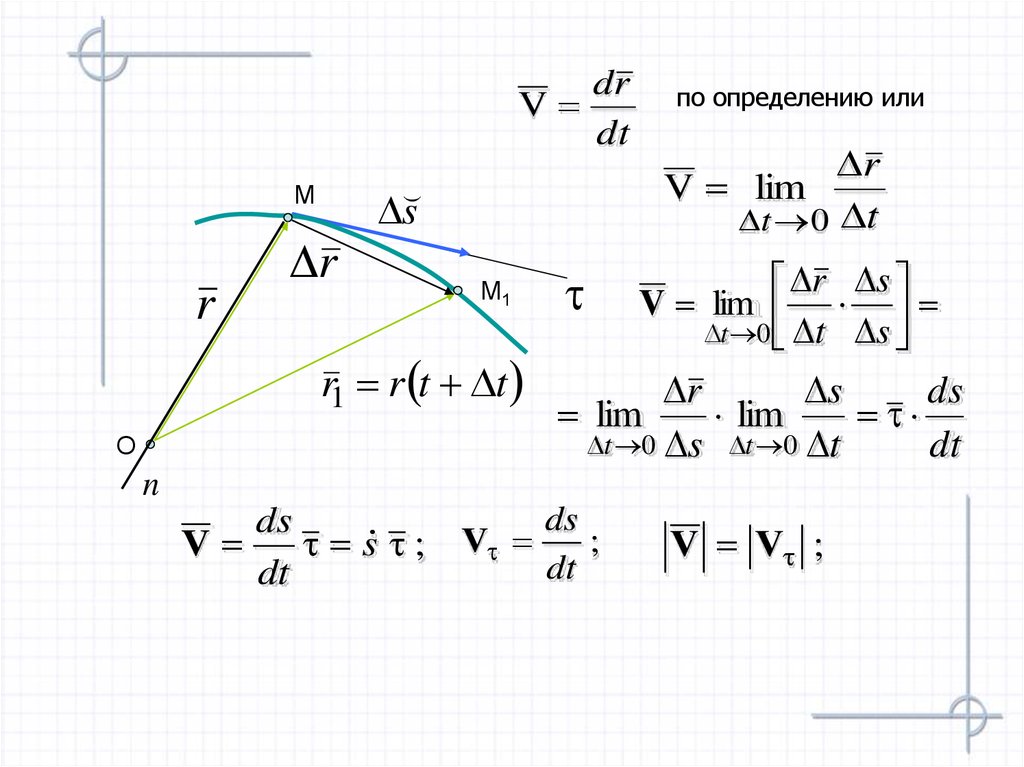
17.
drV
dt
М
r
r
s
М1
r1 r t t
O
по определению или
r
V lim
t 0 t
r s
V lim
t 0 t s
r
s
ds
lim
lim
t 0 s t 0 t
dt
n
ds
ds
V
;
V
s ;
dt
dt
V V ;
18.
2.6. Ускорение при естественномспособе задания движения точки
М V t
угол смежности
V
М1
V t t
O
V V t t V t
V
acp
; acp V
t
V t t
acp лежит в
соприкасаю щейся
плоскости
V
dV
a lim
a
n
a
a
b
;
n
b
dt
t 0 t
19.
VV cos V
V V
dV
lim 1
lim 1
;
t
t 0 t
t 0
t
dt
t 0
a lim
0
V1 sin s
Vn
V sin
lim 1
lim
t
s
t 0
t
t 0
t 0 t
0
an lim
0
s
sin
lim V1
lim
lim
t t 0 s 0
t 0
0
d
k
lim
ds
s 0 s
ab 0
0
t 0
- кривизна кривой
в точке М
2
V
;
V2 k
sin
1
lim
0
20.
1радиус кривизны траектории
k
2
М
О
a
a
an
dV
V
a
n
dt
a
a 2 an2
an
всегда положительное, т.к. всегда направлено в
сторону вогнутости траектории
a
an
показывает изменение скорости по величине
показывает изменение скорости по направлению
21. § 3. Частные случаи движения точки
Равномерное движение, если всегдав случае V 0
a 0
имеем V const
Равномерное прямолинейное движение, когда an 0
и значит
либо если
V2
0
V 0, то мгновенная остановка, т.е.
скорость меняет направление – точка перегиба
Равномерное криволинейное движение, когда a
n
В этом случае уравнение движения
a
s t s0 Vt
22.
Еслиa 0
в какой-нибудь момент времени
имеем экстремум, т.е.
Если
a 0,
Vmax или Vmin
то движение с ускорением
движение ускоренное, когда
a 0
движение замедленное, когда a 0
23.
Равноускоренное движение, если всегдаa const
В этом случае уравнение движения
a const
dV a dt
ds V0 a t dt
V V0 a t
a t 2
s t s0 Vt
2


















 physics
physics








