Вычисление тройных интегралов

1.

Пусть дан тройной интеграл
I f ( x, y, z )dV
V
dV dxdydz

2.

z
V
z1
z2
x
y
N
D

3.

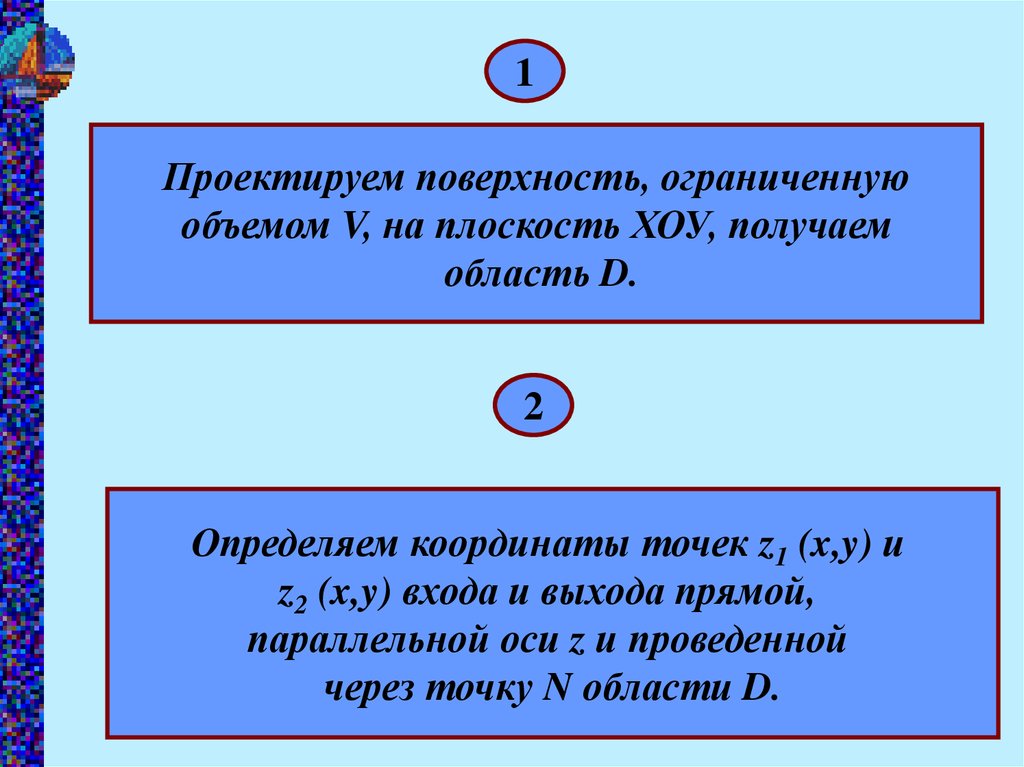
1
Проектируем поверхность, ограниченную
объемом V, на плоскость ХОУ, получаем
область D.
2
Определяем координаты точек z1 (x,y) и
z2 (x,y) входа и выхода прямой,
параллельной оси z и проведенной
через точку N области D.

4.

3
Считая х,у постоянными, вычисляем интеграл:
z2
f ( x, y, z ) dz
z1
А затем двойной интеграл:
z2
dS f ( x, y, z ) dz
D
z1

5.

4
Двойной интеграл можно свести к повторному:
b
y2 ( x ) z 2 ( x , y )
a
y1 ( x )
I dx
dy f ( x, y, z ) dz
z1 ( x , y )

6.

Вычислить тройной интеграл
( x y z )dxdydz
V
где V – область, ограниченная
координатными плоскостями
x=0, у=0, z=0 и плоскостью
x+y+z=1

7.

z
D
x
y

8.

1
По переменной z интегрирование идет от 0 до
z=1-x-y:
1 x y
( x y z)dxdydz dxdy ( x y z)dz
V
D
0
1 x y
z
dxdy ( x y ) z
2 0
D
2
(1 x y) 2
dxdy ( x y) (1 x y)
2
D

9.

2
(1 x y)
2
2
dxdy x y x xy xy y
2
D
2
(
1
x
y
)
2
dxdy ( x y) ( x y)
2
D
2
Теперь расставляем пределы интегрирования по
области D: это треугольник со сторонами x=0,
y=0, x+y=1:

10.

1 x
2
(
1
x
y
)
2
dx dy ( x y) ( x y)
2
0
0
1
( x y ) ( x y ) (1 x y )
dx
3
6
2
0
1
2
3
3
0
1 x 2 1 x3 (1 x)3
dx
6
2 2 3 3
0
1
1 x

11.

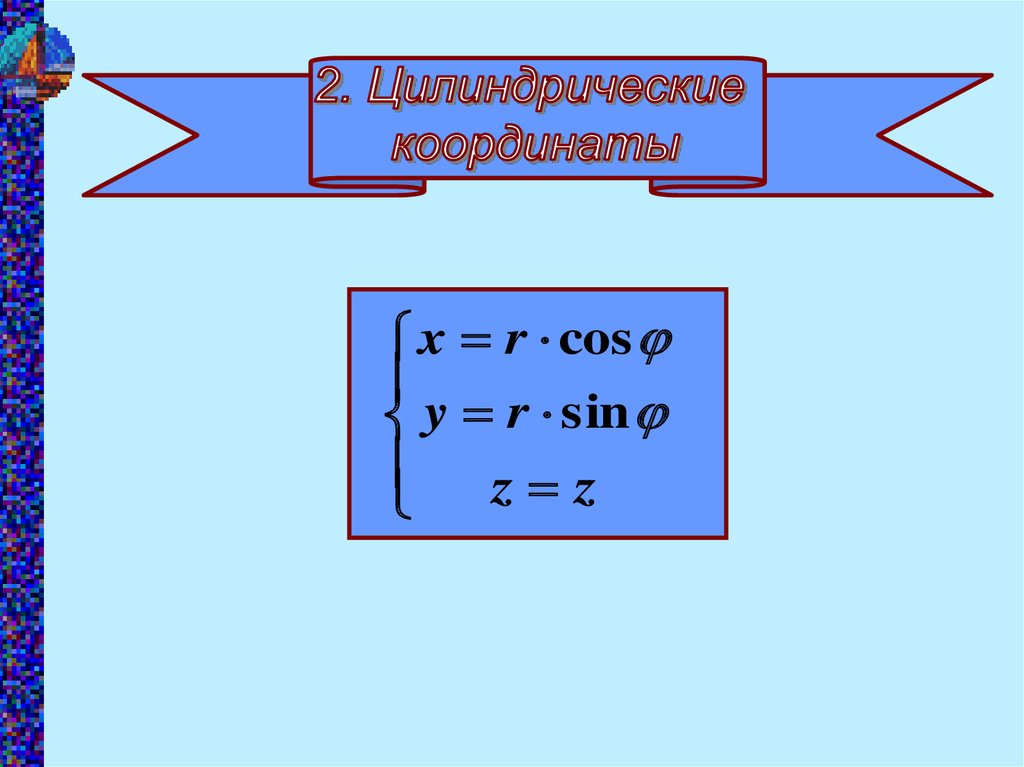
x r cos
y r sin
z z

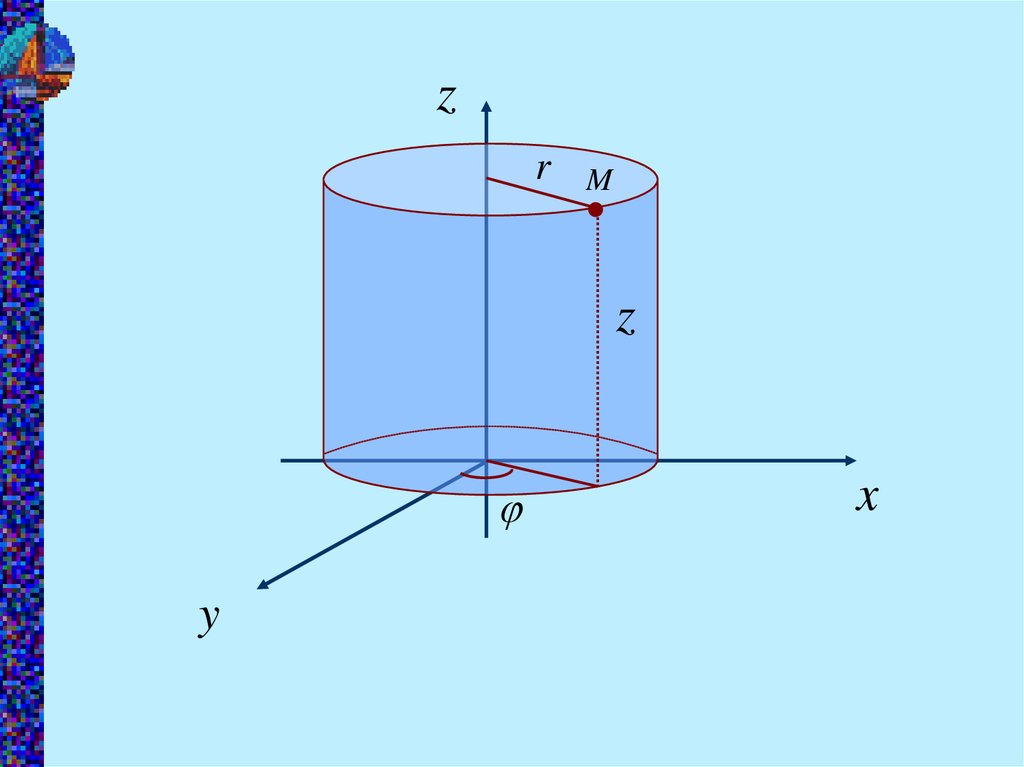
12.

z
r
M
z
y
x

13.

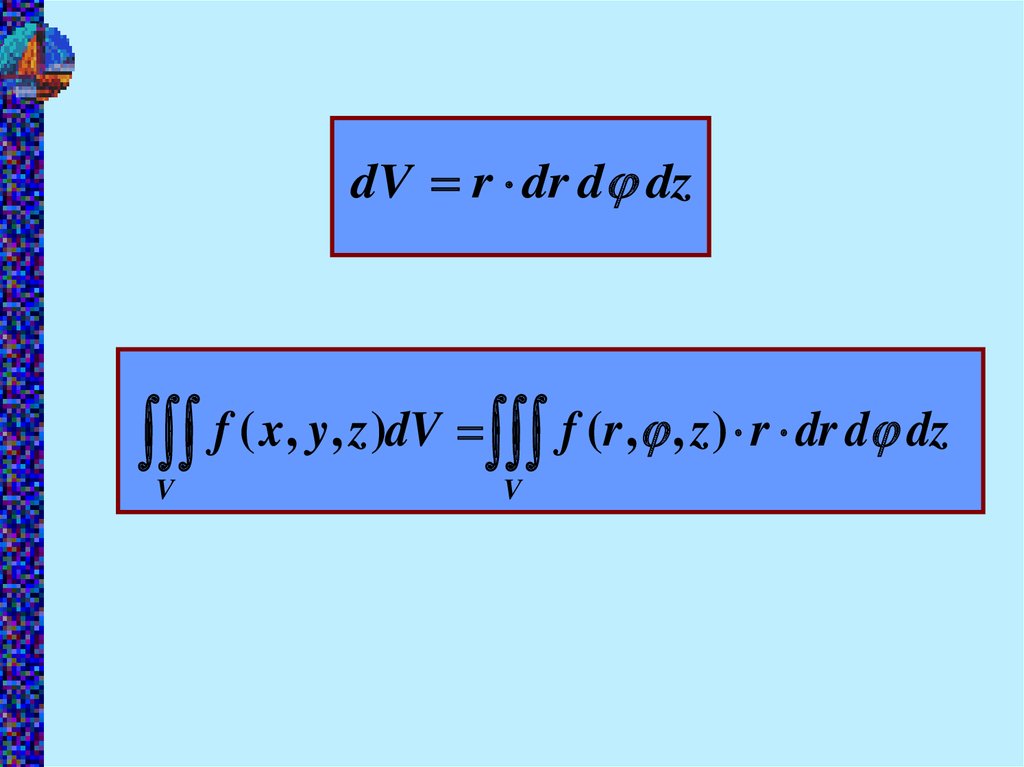
dV r dr d dz
f ( x, y, z )dV f (r , , z ) r dr d dz
V
V

14.

x sin cos
y sin sin
z cos

15.

z
M
x
y

16.

dV sin d d d
2
f ( x, y, z)dV f ( , , )
V
V
2
sin d d d