Similar presentations:
Виды ДУ 1 порядка и методы их решения
1.
1УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ
ПЕРЕМЕННЫМИ
2.
ДУ видаy f1 ( x) f 2 ( y)
4
где f1(x) и f2(y) – непрерывные функции,
называется уравнением с разделяющимися
переменными.
3.
Правая часть такого уравнения представляет собойпроизведение, в котором один сомножитель зависит
только от х, а другой – от у.
Метод решения таких уравнений называется
методом разделения переменных.
Для его использования запишем производную как
отношение
дифференциала
функции
к
дифференциалу независимой переменной:
dy
y
dx
4.
Теперь уравнение нужно преобразовать к виду, вкотором дифференциал и функция переменной х
окажутся в одной части равенства, а переменной у –
в другой:
dy
f1 ( x) f 2 ( y )
dx
dy
f1 ( x) dx
f 2 ( y)
Пусть у=φ(х) является решением уравнения (4).
Тогда подставляя у=φ(х), получим тождество: два
дифференциала равны друг другу. При этом справа
дифференциал выражен через переменную х, а
слева – через у.
5.
Так как дифференциалы равны, то неопределенныеинтегралы от этих выражений будут отличаться на
произвольную постоянную величину:
dy
f1 ( x) dx C
f 2 ( y)
6.
1Найти частное решение уравнения
x y y 0
при у0 =4, х0 =-2.
7.
dyx y 0
dx
dy
dy y
x
y
dx
dx x
dy dx
dy
dx
y
x
y
x
ln y ln x C
C ln C1
ln y ln x ln C1 ln C1 x
8.
Потенцируем:y C1 x
y C1 x
C1 C2
y C2 x
Это общее решение уравнения, описывающее
семейство интегральных кривых.
Для нахождения частного решения подставим
начальные условия:
4 2 C2 C2 2
Частное решение будет иметь вид:
y 2 x
9.
2Найти общее решение уравнения
( x 2 y ) y 1
10.
Сделаем замену:z 1 1
x 2 y z z 1 2 y y
z 1
2
2
Тогда уравнение будет иметь вид:
1
z z 1 1
2
1
1
z z z 1
2
2
1
1 z
1 dz 1
dz
2
z z 1
1
2 dx 2
dx
z
2
11.
dz 2 zdx
z
z
dz dx
2 z
z
2 z dz dx
z 2 2
2
x
dz dz
dz z 2 ln z 2 C
z 2
z 2
Возвращаемся к старым переменным:
x x 2 y 2 ln x 2 y 2 C
1
C1 C
2
y ln x 2 y 2 C1
12.
2НЕПОЛНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
ДУ первого порядка называется неполным,
если функция явно зависит только от
одной переменной (х или у).
13.
1Пусть функция зависит только от х.
dy
f ( x) dy f ( x)dx
dx
Решением этого уравнения будет
y f ( x)dx C
14.
2Пусть функция зависит только от у.
dy
f ( y)
dx
dy
dx
f ( y)
Решением этого уравнения будет
x
dy
C
f ( y)
dy
dx
f ( y)
15.
Найти общее решение уравненияy y
16.
dyy
dx
dy
dx
y
ln y x C
dy
y dx
y e x C e x eC
e C1
C
y e
x C
C1e
x
y C1e C2e
x
x
17.
3ЛИНЕЙНЫЕ ДУ ПЕРВОГО ПОРЯДКА
ДУ первого порядка называется линейным,
если оно имеет вид
y f ( x) y g ( x)
5
18.
Функции f(x) и g(x) – непрерывны.Неизвестная функция и ее производная входят в
такое уравнение линейно.
Если g(x)=0, то уравнение называется
однородным.
Если g(x) не равно 0, то уравнение
называется неоднородным.
19.
Для решения неоднородного ДУ первого порядкаиспользуется
Сначала решается однородное уравнение методом
разделения переменных:
dy
dy
y f ( x) y 0
f ( x) y
f ( x)dx
dx
y
ln y f ( x)dx C
y e
f ( x ) dx C
e
f ( x ) dx
eC
20.
e C1C
y C1e
f ( x ) dx
C1 C2 y C2e
f ( x ) dx
Это получено решение однородного ДУ.
Теперь ищем общее решение неоднородного ДУ.
Будем полагать, что С2 является новой неизвестной
функцией от х: С2(х), т.е.
y C2 ( x) e
f ( x ) dx
21.
Подставляем это выражение в исходное уравнение(5) и находим неизвестную функцию С2(х).
y C2 ( x) e
C2 ( x) e
f ( x ) dx
C2 ( x ) e
f ( x ) dx
C2 ( x) f ( x)e
f ( x ) dx
C2 ( x) f ( x)e
f ( x ) dx
f ( x ) dx
C2 ( x) f ( x)e
f ( x ) dx
g ( x)
f ( x ) dx
g ( x)
g ( x ) C2 ( x )
g ( x) e
f ( x ) dx
e
22.
Интегрируем последнее выражение:f ( x ) dx
C2 ( x) g ( x) e
dx C3
Результат интегрирования подставляем в общее
решение однородного уравнения:
y e
f ( x ) dx
f ( x ) dx
g ( x) e
dx C3
Это получено общее решение неоднородного ДУ.
23.
1Найти общее решение уравнения
2
2
y x y x
24.
Решаем однородное уравнение методом разделенияпеременных:
y x y 0
2
dy
x2 y
dx
dy
x 2 dx
y
3
dy
x
2
y x dx ln y 3 C
y e
x3
C
3
e
y C1 e
x3
3
x3
3
eC C1 e
C2 e
x3
3
x3
3
25.
Получили решение однородного ДУ.Теперь ищем общее решение неоднородного ДУ.
Полагаем, что С2 является новой неизвестной
функцией от х: С2(х), т.е.
3
y C2 ( x) e
y C2 ( x ) e
x3
3
x
3
C2 ( x ) x e
2
x3
3
Подставляем в исходное уравнение:
C2 ( x ) e
x3
3
C2 ( x ) x 2 e
x3
3
C2 ( x) x 2 e
x3
3
x2
26.
C2 ( x ) ex3
3
x
2
C2 ( x) x e
2
x3
3
Интегрируем:
x3
3
x3
3
1
3
C2 ( x) x e dx e d ( x ) e
3
2
Подставляем
уравнения:
y e
в
x3
3
общее
e
x3
3
решение
x3
3
C3
однородного
C3 1 C3 e
x3
3
27.
2Найти общее решение уравнения
x y y e x
28.
Решаем однородное уравнение методом разделенияпеременных:
dy
y
dy
dx
x y y 0
dx
x
y
x
dy
dx
y x ln y ln x C1
C2
1
y
y C2
x
x
29.
Получили общее решение однородного ДУ.Теперь ищем общее решение неоднородного ДУ.
Полагаем, что С2 является новой неизвестной
функцией от х: С2(х), т.е.
C2 ( x )
C2 ( x) x C2 ( x)
y
y
x
x2
Подставляем в исходное уравнение:
C2 ( x) x C2 ( x) C2 ( x)
x
x
e
2
x
x
30.
C2 ( x ) C2 ( x)x
C2 ( x )
e
x
x
x
C2 ( x ) e
Интегрируем:
C2 ( x) e dx e C3
x
Подставляем
уравнения:
в
x
общее
решение
1 x
y e C3
x
однородного






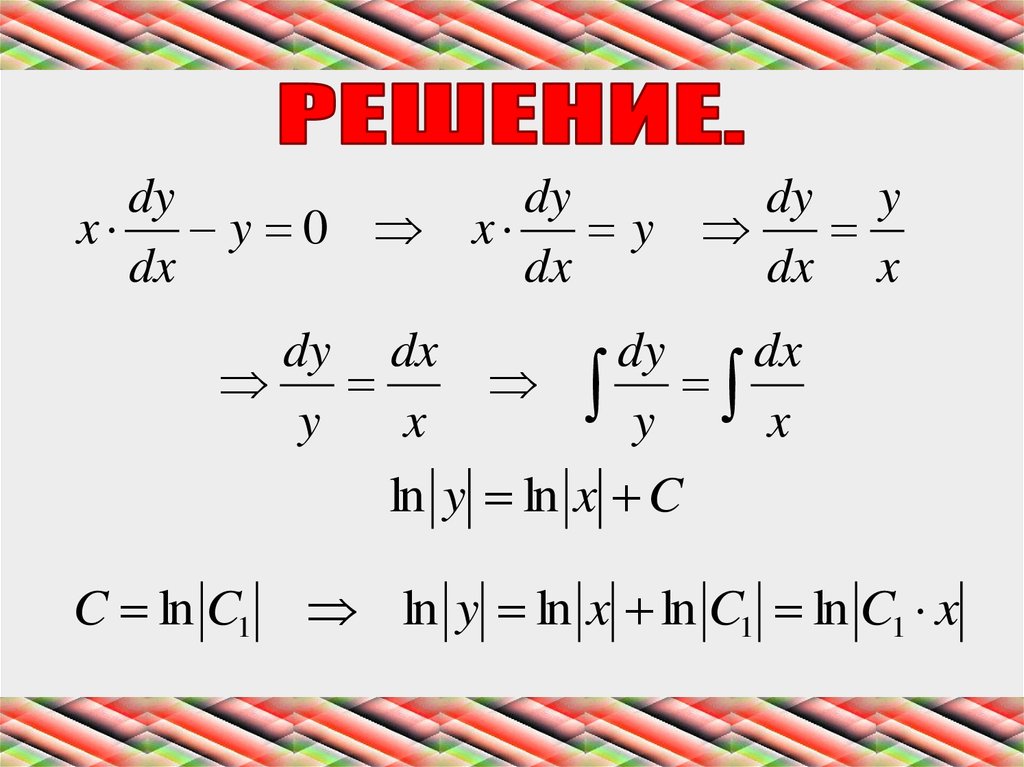























 mathematics
mathematics








