Similar presentations:
Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение
1. Обыкновенные дифференциальные уравнения 1 порядка Классификация и решение
2.
Однородные уравнения.Определение. Функция f(x, y) называется однородной n – го
измерения относительно своих аргументов х и у, если для любого
значения параметра t (кроме нуля) выполняется тождество:
f (tx, ty) t f ( x, y).
n
Определение. Дифференциальное уравнение вида
y f ( x, y )
называется однородным, если его правая часть f(x, y) есть
однородная функция нулевого измерения относительно своих
аргументов.
Сводится заменой
y = ux
к уравнению с разделяющимися
переменными относительно неизвестной
функции u
3.
Уравнения, приводящиеся к однородным.Это класс уравнений, которые с помощью определенных
подстановок могут приведены к однородным.
ax by c
y f
a1 x b1 y c1
Если определитель
a
b
a1 b1
x u ;
0, то
y v ;
переменные могут
разделены подстановкой
быть
где и - решения системы уравнений
ax by c 0
a1 x b1 y c1 0
4.
В случае если в исходном уравнении видаax by c
y f
a1 x b1 y c1
определитель
a
b
a1 b1
0,
то переменные могут быть разделены подстановкой
ax by t.
5.
Линейные уравнения первого порядкаy P( x) y 0
Этот тип дифференциальных уравнений называется линейным
однородным (ЛОДУ1) и оно является уравнением с
разделяющимися переменными. Поэтому
dy
P( x)dx
y
Общее решение:
ln y P( x)dx ln C ;
y Ce
P ( x ) dx
ln
y
P( x)dx;
C
6.
Линейные неоднородные дифференциальные уравнения.y P( x) y q( x)
Для интегрирования линейных неоднородных уравнений (ЛНДУ1)
(q(x) 0) применяются в основном два метода: метод Бернулли и
метод Лагранжа.
Метод Бернулли.
Суть метода заключается в том,
что искомая функция представляется в виде произведения двух
функций
y uv
7.
При этом очевидноВыполняем замену:
dv
du
v
dx
dx
dv
du
u v
P( x)uv q( x)
dx
dx
y u
dv du
u v
P( x)u q ( x)
dx dx
Далее следует важное замечание
первоначальная функция была представлена нами в виде произведения
Поэтому каждый из сомножителей, входящих в это произведение,
может быть произвольным, выбранным по нашему усмотрению.
Например, функция
y 1 2x 2 ;
y 2x 2 может быть представлена как
y 2 x2;
y 2 x x;
и т.п.
8.
Выбор всегда направлен на простоту результата. Поэтому одну изсоставляющих произведение функций выбрать так, что выражение
в скобках будет равно нулю.
du
P( x)u 0(*)
dx
Таким образом, наше уравнение будет равносильно системе двух
уравнений. Каждое из них - это дифференциальное уравнение с
разделяющимися переменными. Первое уже получено. В него входит
только ОДНА из новых функций и его можно решить по
представленной выше схеме. При этом в записи решения произвольную
постоянную добавлять не нужно, ведь мы искали не ВСЕ решения, а
лишь ОДНУ функцию, именно ту, которая удовлетворяет
поставленному условию.
Для нахождения второй неизвестной функции
подставим поученное выражение для функции u
в исходное уравнение
9.
udv du
v
P( x)u q ( x)
dx dx
с учетом того, что выражение, стоящее в скобках, равно нулю
Получаем второе уравнение нашей системы.
Очевидно, найденную первую функцию нужно было выразить явно и
в этом уравнении (снова с разделяющимися переменными!)
останется лишь одна неизвестная.
dv
u
q (x)(**)
dx
Окончательно получаем
y uv
Произвольная постоянная учитывается при записи одного из
сомножителей
10.
Метод Лагранжа.Метод
Лагранжа
решения
неоднородных
линейных
дифференциальных уравнений еще называют методом вариации
произвольной постоянной. Мы с вами встретимся с этим методом
решая уравнения старших порядков
Вернемся к поставленной задаче:
y P( x) y q ( x)
Первый шаг данного метода состоит в отбрасывании правой
части уравнения и замене ее нулем.
y P( x) y 0
Далее
находится
решение
получившегося
однородного
дифференциального уравнения (его решают как уравнение с
P ( x ) dx
разделяющимися переменными):
y C1e
11.
Длятого,
чтобы
найти
соответствующее
решение
неоднородного дифференциального уравнения, будем считать
постоянную С1 некоторой функцией от х. Вариьруем её, отсюда
название «метод вариации»
Тогда по правилам дифференцирования произведения функций
получаем:
P ( x ) dx
dy dC ( x) P ( x ) dx
y
dx
1
dx
e
C1 ( x)e
( P( x));
Подставляем полученное соотношение в исходное уравнение
P ( x ) dx
P ( x ) dx
dC1 ( x) P ( x ) dx
e
C1 ( x) P( x)e
P( x)C1 ( x)e
q( x)
dx
12.
Из полученного уравненияdC1 ( x) P ( x ) dx
e
q ( x);
dx
определим переменную функцию С1(х):
P ( x ) dx
dC1 ( x) q( x)e
dx;
Интегрируя уравнение с разделяющимися переменными, получаем:
y e
P ( x ) dx
q( x)e P ( x ) dx dx C
При выборе метода решения линейных дифференциальных уравнений
следует руководствоваться
простотой интегрирования функций,
входящих в исходный интеграл.
Совет: в своих работах использовать метод Бернулли
13.
12 x
x 2 y y 6 x e .
Пример. Решить уравнение
Сначала приведем данное уравнение к стандартному виду:
1
1
y 2 y 6e x .
x
1
1
P 2 ; q 6e x ;
x
Применим полученную выше формулу для
y e
1
dx
x2
1
1
dx
2
x
x
6e e
dx
C
1 1
1
x
x
y e 6e e dx C e x 6dx C
1
x
ОТВЕТ:
Общее решение
1
x
y e (6 x C ).
14.
Уравнение Бернулли.Определение. Уравнением Бернулли называется уравнение вида
y Py q y n ,
где P и q – функции от х или постоянные числа, а n – постоянное
число, не равное 1.
Для решения уравнения Бернулли используют 2 варианта:
1)можно применить метод Бернулли и решать аналогично ЛДУ1
2) сначала применяют подстановку
z
1
y
n 1
с помощью которой, уравнение Бернулли приводится к линейному.
15.
Для этого разделим исходное уравнение на yn.y
1
P
q
n
n 1
y
y
n 2
(
n
1
)
y
(n 1) y
Применим подстановку, учтя, что z
y
2 n 2
y
yn
z
n 1
Pz q
z (n 1) Pz (n 1)q
Как видите,
получилось линейное уравнение относительно
неизвестной функции z.
16. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
Уравнение вида(
n
) f(x
y
)
решается последовательным n-кратным
интегрированием.
Умножаем обе части уравнения на dx:
(
n
)
y
dx
f
x
dx
(
n
)
y
dx
x
dx
f
Интегрируем:
Получаем уравнение (n-1)-го порядка:
,
где
(
n
1
)
y
F
x
C
1
1
первообразная для f(x)
F1(x)
Снова умножаем обе части на dx и интегрируем:
или
(
n
2
)
y
F
(
x
)
C
)
dx
(
1
1
и т.д.
(
n
2
)
y
F
(
x
)
C
x
C
2
1
2
Общее решение будет зависеть от n произвольных констант
17. Пример.
y 60x2 dxy dx 60x2dx y dx 60x2dx
3
x
y 60 x2dx y 60
C
3
1
y 20x3 C1 dx
y dx (20x3 C1)dx y dx (20x3 C1)dx
y 5x4 C1x C2 dx
y dx (5x4 C1x C2)dx y dx (5x4 C1x C2)dx
2
x
y x5 C1
C2x C3
2
















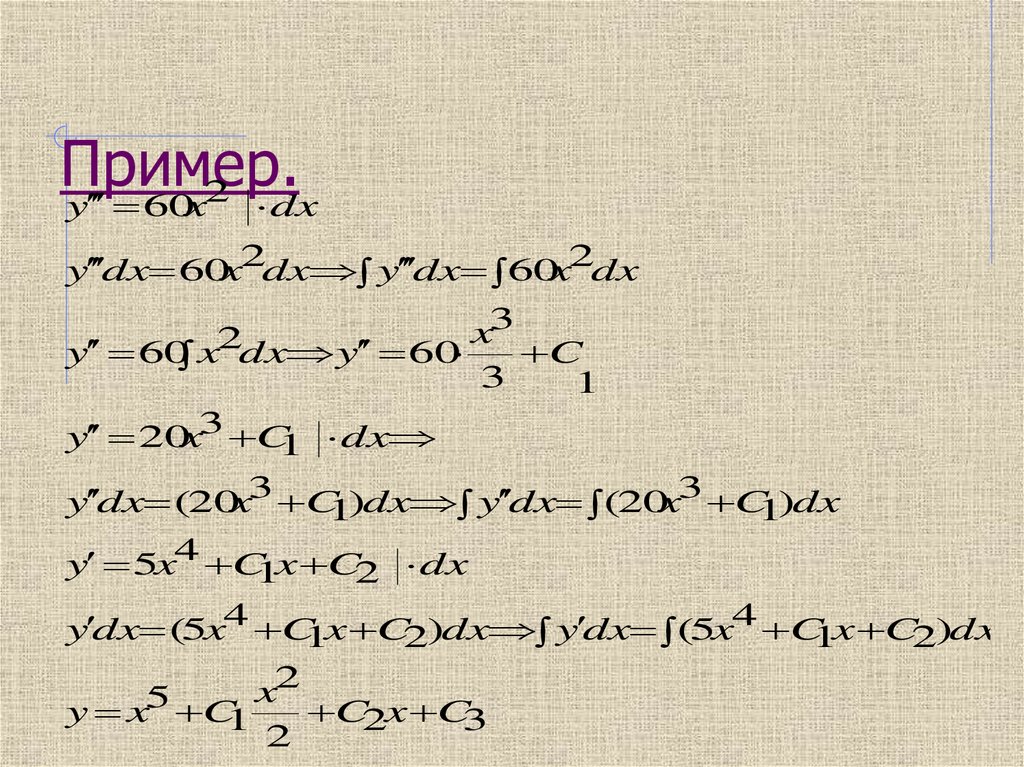
 mathematics
mathematics








