Similar presentations:
Решение НЛДУ второго порядка с постоянными коэффициентами методом неопределённых коэффициентов
1. Математика Часть 2
УГТУ-УПИ2007 г.
2.
1.Решение НЛДУ второго порядка с
постоянными коэффициентами методом
неопределённых коэффициентов.
Для НЛДУ с постоянными коэффициентами
существует более простой метод нахождения
частного решения y% , чем метод вариации
произвольных постоянных.
Частное решение НЛДУ зависит от вида правой
a1 y
a2 y f x .
части уравнения y
Если
1.
где
f x Pn x e
x
Pn x многочлен n-го порядка.
3.
Возможны следующие случаи:1) не является корнем характеристического
2
уравнения k a1k a2 0,
частное решение
y% Qn x e
x
y% ищем в виде:
A0 x A1 x
n
n 1
... An e .
x
y%
Qn
x e Qn x e ,
x
x
y%
Qn
x e Qn
x e
x
Qn
x e
x
x
Qn x e
2 x
,
4.
Qnx 2Qn x Qn x a1Qn x
2
a1Qn x a2Qn x Pn x
Qn
x Qn
x 2 a1
Qn x a1 a2 Pn x
2
Слева и справа от знака равенства –
Pn x , Qn x
многочлены степени n
Приравнивая коэффициенты при одинаковых
степенях x , получим систему n 1
уравнений для определения коэффициентов
A0 , A1 ,..., An .
5.
Пример .Найти общее решение НЛДУ
y
5 y
6y e .
x
Решение.
Для ОЛДУ
k 5k 6 0,
2
k1 3, k 2 2, y0 c1e c2 e
x
f x e
1.
Для
x
k1 , k2
y% Ae
Так как
3x
2x
.
6.
y%Ae ,
y%
Ae .
x
Найдем А.
x
Подставим в уравнение:
1
Ae 5 Ae 6 Ae e , 2 A 1, A
2
1 x
y% e
2
y y0 y%
Общее решение НЛДУ:
x
x
y c1e
x
3x
x
c2 e
2x
1 x
e .
2
7.
2) - простой (однократный) кореньхарактеристического уравнения.
x
%
Частное решение искать в форме y Qn x e
2
нельзя, т.к. в равенстве a1 a2 0.
Слева от знака равенства – многочлен
степени n 1 , справа – степени n
Тождество не получается ни при каких
A0 , A1 ,..., An
Частное решение
y% ищем в виде:
y% xQn x e
x
8.
3) - двукратный корень характеристическогоуравнения.
x
%
Частное решение искать в форме y Qn x e
нельзя, т.к. в равенстве
2
a1 a2 0,
2 a1 0
Слева от знака равенства – многочлен
степени n 2 , справа – степени n
Чтобы получить тождество многочленов,
частное решение
y% ищем в виде:
2
x
%
y x Qn x e
9.
Пример .Найти общее решение НЛДУ
y
8 y
16 y e .
4x
Решение.
Для ОЛДУ
k 8k 16 0,
2
k1 4, k2 4,
4x
Для f x e
Так как
y0 c1e
4.
k1 = k2 4
2
4x
%
y x Ae
4x
c2 xe .
4x
10.
Найдем А.4x
2
4x
4x
2
%
y 2 xAe x A4e e 2 Ax 4 Ax ,
4x
2
4x
y%
4e 2 Ax 4 Ax e 2 A 8 Ax
4x
2
e 8 Ax 16 Ax 2 A 8 Ax
e
e
4x
16 Ax
2
4x
16 Ax
2
16 Ax 2 A ,
16 Ax 2 A 8e
4x
2 Ax 4 Ax
2
16 x Ae e ,
2
4x
4x
16 Ax 16 Ax 2 A 16 Ax 32 Ax 16 Ax 1
2
2
2
11.
1 2 4xy% x e
2
1
2 A 1, A
2
y c1e
4x
c2 xe
4x
1 2 4x
xe .
2
12.
2. Еслиx
x
f x Pn x e cos x Qm x e sin x
где Pn x , Qm x многочлены.
Возможны следующие случаи:
1) если i не является корнем
характеристического уравнения, то
y% U p x e cos x V p x e sin x
x
где
x
U p x ,V p x многочлены,
степень которых равна наивысшей степени
многочленов Pn x , Qm x , p max m , n
.
13.
2) если i является корнемхарактеристического уравнения, то
x
x
%
y x
U p x e cos x V p x e sin x
Замечание.
Вид частного решения сохраняется в случае,
когда один из многочленов Pn x , Qm x
равен нулю.
14.
Пример .Найти общее решение НЛДУ
y
4 y
4 y cos x .
Решение.
Для ОЛДУ
k1 2,
Для
k 4k 4 0,
2
k 2 2,
f x cos x
Так как
y0 c1e
2x
c2 xe .
i 0 i1.
k1,2 2 i
y% A cos x B sin x
2x
15.
Найдем А и В.y%
A sin x B cos x ,
y%
A cos x B sin x ,
A cos x B sin x 4 A sin x B cos x
4 A cos x B sin x cos x
A 4B 4 A cos x B 4 A 4 B sin x cos x
3 A 4 B 1,
4 A 3B 0
3
4
A ,B
25
25
16.
34
y% cos x sin x ,
25
25
y c1 e
2x
c2 xe
2x
3
4
cos x sin x .
25
25
17.
Пример .Найти общее решение НЛДУ
y
y 3sin x .
Решение.
Для ОЛДУ
k1,2
i,
k 1 0,
2
y0 c1 cos x c2 sin x
f x 3sin x i 0 i1.
i совпадает с i i
Так как k1,2
y% x A cos x B sin x
Для
18.
Найдем А и В.y%
A cos x B sin x xA sin x xB cos x
A Bx cos x B Ax sin x ,
y%
B cos x A Bx sin x
A sin x B Ax cos x
B B Ax cos x A Bx A sin x ,
2 B Ax cos x 2 A Bx sin x
Ax cos x Bx sin x 3sin x ,
19.
2 B cos x 2 A sin x 3sin x .2 A 3,
2B 0
3
A ,B 0
2
3
y% x cos x
2
3
y c1 cos x c2 sin x x cos x .
2
20.
Т. Принцип суперпозиции решений.a1 y
a2 y f1 x f 2 x ,
Пусть y
y%
a1 y
a 2 y f1 x ,
1 - частное решение y
y%
a1 y
a2 y f 2 x ,
2 - частное решение y
тогда частное решение НЛДУ равно сумме
%
этих двух решений y% y%
1 y2
21.
2. Решение НЛДУ высших порядков .y
n
где
a1 y
ai
n 1
... an y f x ,
i 1, 2, ..., n , f x
непрерывные функции или постоянные.
Пусть общее решение соответствующего
однородного уравнения
y0 c1 y1 c2 y2 ... cn yn
22.
Т. Метод вариации произвольных постоянныхЧастное решение НЛДУ ищется в виде:
y% c1 x y1 c2 x y2 ... cn x yn
где c1 x , c2 x ,...,cn x
функции, определяемые из системы уравнений
c1
y1 c2
y2 ... cn
yn 0,
c1 y1 c2 y2 ... cn
yn 0,
....................
n 1
n-1
n 1
c1
y1
c2
y2 ... cn
yn f x
23.
Метод неопределенных коэффициентов1.
f x Pn x e
Если
x
возможны следующие случаи:
1) не является корнем характеристического
уравнения.
y% ищем в виде:
Частное решение
y% Qn x e
x
A0 x A1 x
n
n 1
x
... An e .
24.
2) - корень характеристического уравнениякратностиm
.
y% ищем в виде:
Частное решение
y% x Qn x e
m
x
25.
Пример .Найти общее решение НЛДУ
y
4
y x 1.
3
Решение.
Для ОЛДУ
k1 1,
k 1 0,
k2 1, k3 i ,
4
y0 c1e c2e
x
Для
3
x
k4 i ,
c3 cos x c4 sin x .
f x x +1
0 k1 , k 2 , k 3 , k4 .
y% Q3 x e A0 x A1 x A2 x A3 .
0x
3
2
26.
A0 , A1 , A2 , A3 .Найдем
y%
3 A0 x 2 A1 x A2 ,
y%
6 A0 x 2 A1 , y%
6 A0 ,
2
4
y% 0,
A0 x A1 x A2 x A3 x 1.
3
2
3
Приравниваем коэффициенты при одинаковых
степенях x :
A0 1,
A1 0,
A2 0,
A3 1
y% x 1.
3
27.
y c1 e c2 ex
x
c3 cos x c4 sin x x 1.
3
28.
2. Еслиf x Pn x e cos x Qm x e sin x
x
x
Возможны следующие случаи:
1) если i
не является корнем
характеристического уравнения, то
y% U p x e cos x V p x e sin x
x
x
где U p x ,V p x многочлены,
степень которых равна наивысшей степени
многочленов Pn x , Qm x , p max m , n .
29.
2) если iявляется корнем
характеристического уравнения кратности m ,
то
y% x
m
U x e
p
x
cos x V p x e sin x
x
30.
Пример .Найти общее решение НЛДУ
y
4
y 6sin x .
Решение.
Для ОЛДУ
k1 1,
k 1 0,
k2 1, k3 i ,
4
y0 c1e c2e
x
x
k4 i ,
c3 cos x c4 sin x .
f x 6sin x
0, 1.
i i совпадает с корнем k3 i
Для
y% x A cos x B sin x
31.
Найдем А и В.y%
A Bx cos x B Ax sin x ,
y%
B B Ax cos x A Bx A sin x ,
y%
3 A Bx cos x 3 B Ax sin x ,
y% 4 B Ax cos x 4 A Bx sin x ,
4
4 B Ax cos x 4 A Bx sin x
Ax cos x Bx sin x 6sin x ,
32.
4 B cos x 4 A sin x 6sin x .4 A 6,
4 B 0
3
A ,B 0
2
3
y% x cos x
2
y c1e c2 e
x
x
c3 cos x
3
c4 sin x x cos x .
2
33.
3. Системы линейных уравнений.Определение.
y1( p ) f1 ( x, y1 ,..., y n ( p 1) ),
(p )
( p 1)
f 2 ( x, y 2 ,..., y n
),
(1) y 2
(p )
( p 1)
f n ( x, y1 ,..., y n
)
y n
1
1
2
2
n
n
Система ДУ (1) называется канонической порядка n,
где n = p1 + p2 + … + pn.
34.
Определение.Если p1 = p2 = … = pn = 1, то система (1)
называется нормальной. Она имеет следующий вид
(2)
y1 ' f1 x , y1 , y2 , ..., yn ,
y2 ' f 2 x , y1 , y2 , ..., yn ,
................
y ' f x , y , y , ..., y
n
1
2
n
n
35.
Решением системы (2) на (a,b) называетсясовокупность функций
y1 = у1(х), у2 = у2(х), … , уn = уn(х),
непрерывно
дифференцируемых
на
(a,b)
и
обращающих каждое уравнение системы (2) в верное
равенство.
Общее решение системы (2) – совокупность
функций
y(x, c1, c2, … cn),
зависящих
от
n
произвольных
постоянных
интегрирования
и
обращающих систему (2) в систему верных равенств.
36.
УтверждениеДУ n-го порядка всегда можно свести к
нормальной системе.
Систему ДУ, записанную в каноническом виде
всегда можно свести к нормальному виду.
Обратно: система ДУ, как правило, но не всегда,
сводится к ДУ n-го порядка, решая которое можно
найти решение системы.
37.
Пример.y1 " 2 y1 3 y2 ,
–
каноническая
система
четвертого
y2 " y1 2 y2
порядка.
Обозначим:
y1' = у3, у2' = у4.
y1 ' y3 ,
Тогда
y ' y ,
2
4
y3 ' 2 y1 3y 2 , – нормальная система четвертого
y 4 ' y1 2 y 2
порядка.
38.
Задача Коши для нормальной системыДаны система ДУ (2) и начальные условия
y1(x0) = y10,..., yn(x0) = yn0.
Найти решение системы y1(x), y2(x), … ,yn(x).
Решение.
1. y y ( x , c ,..., c ),
1 1
1
n
y 2 y 2 ( x, c 2 ,..., cn ),
y y ( x, c ,..., c )
n
1
n
n
2. c1, c2, … cn из НУ
39.
Пример решения системыисключения неизвестных.
y ' z,
z ' y
Решение.
из второго уравнения:
y = z'
y' = z"
z" – z = 0
λ² – 1 = 0 λ1,2 = ±1
Ответ. z = с1·e x + с2·e -x ,
y = с1·e x - с2·e -x
ДУ
методом








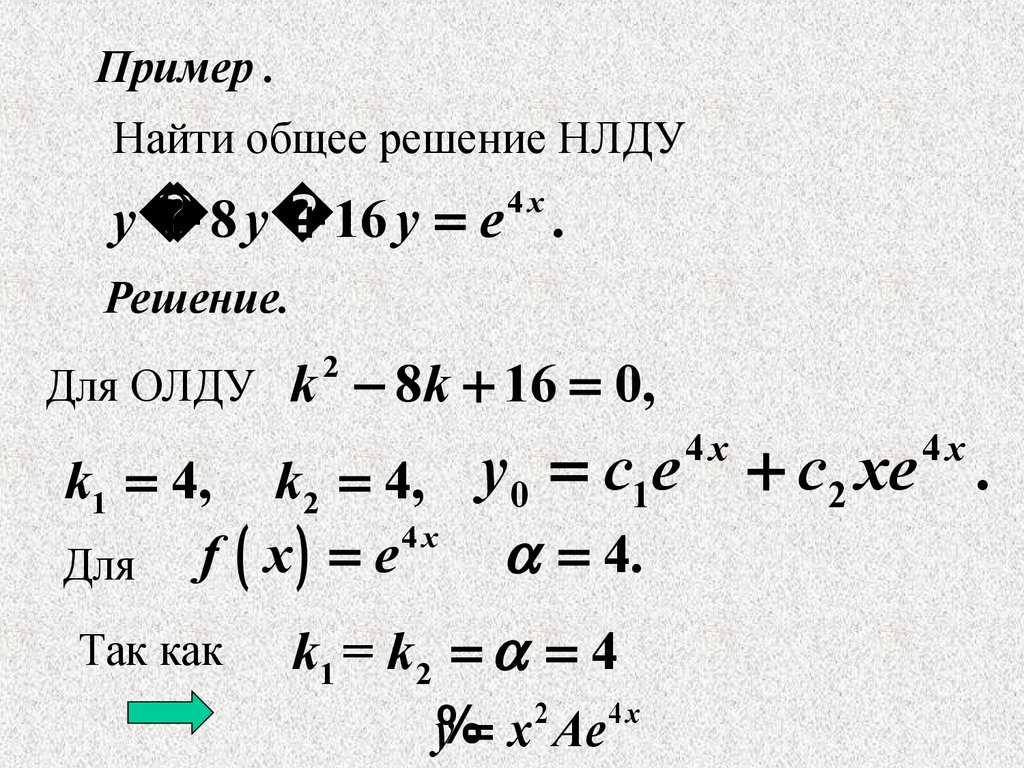
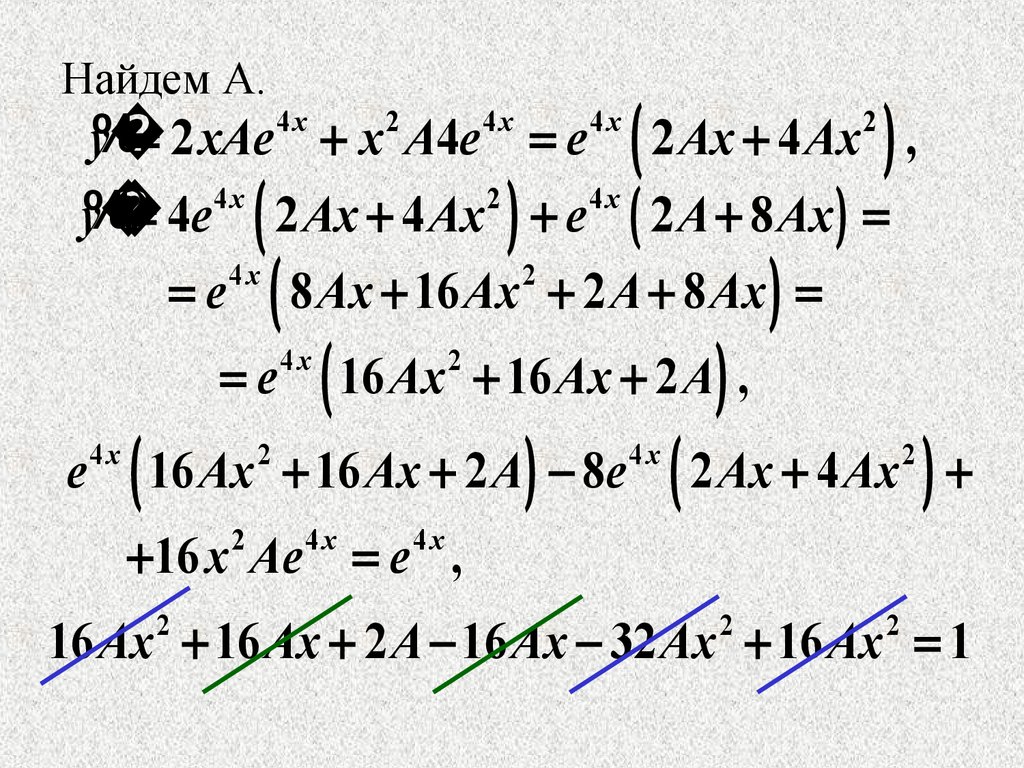



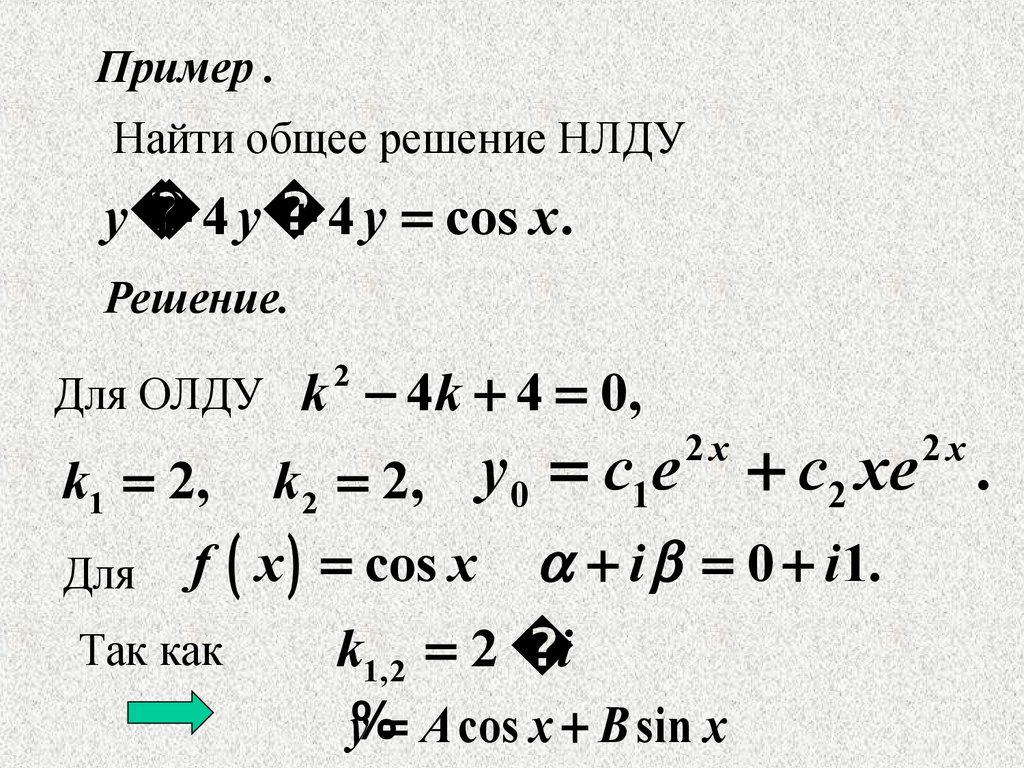
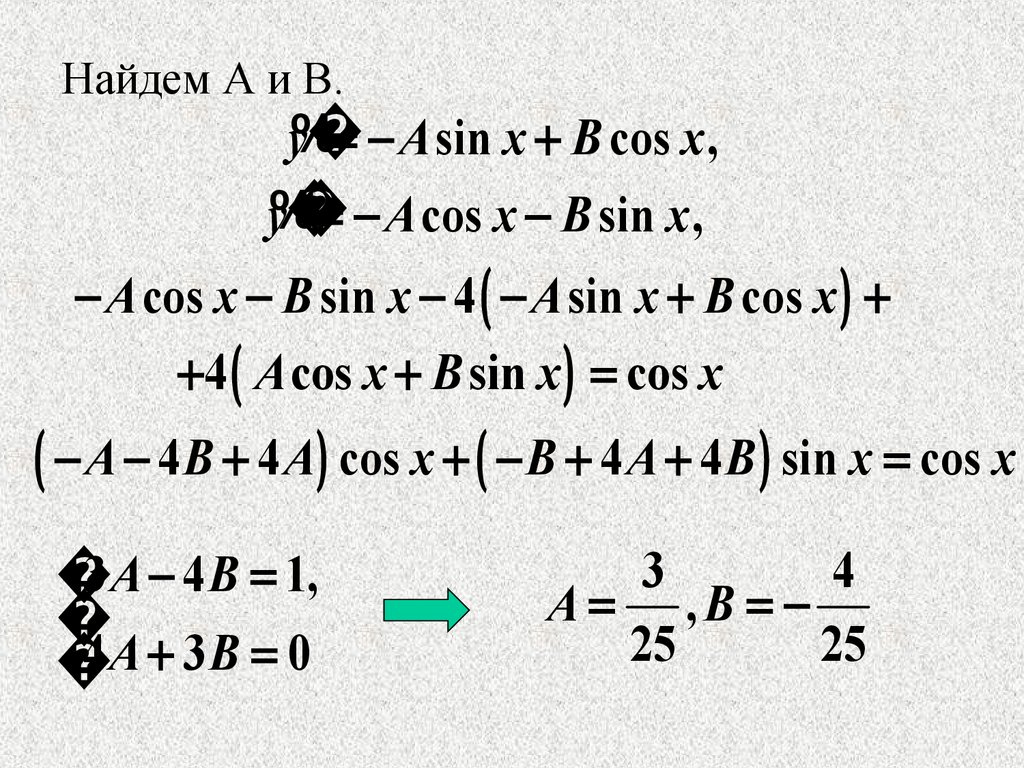

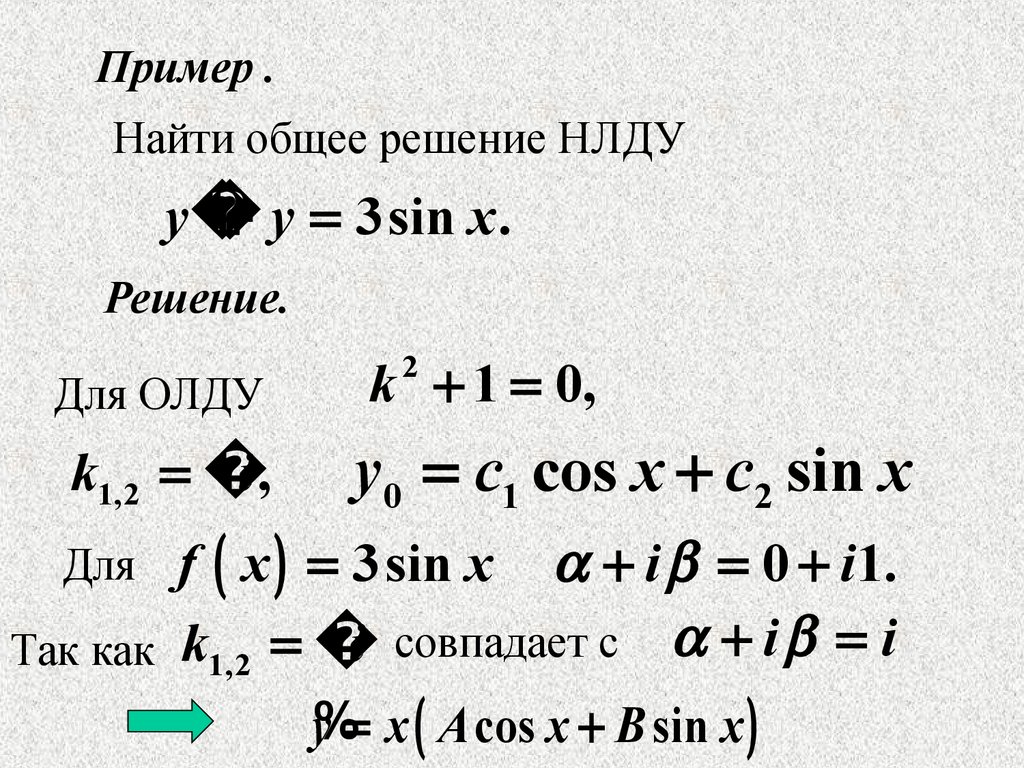
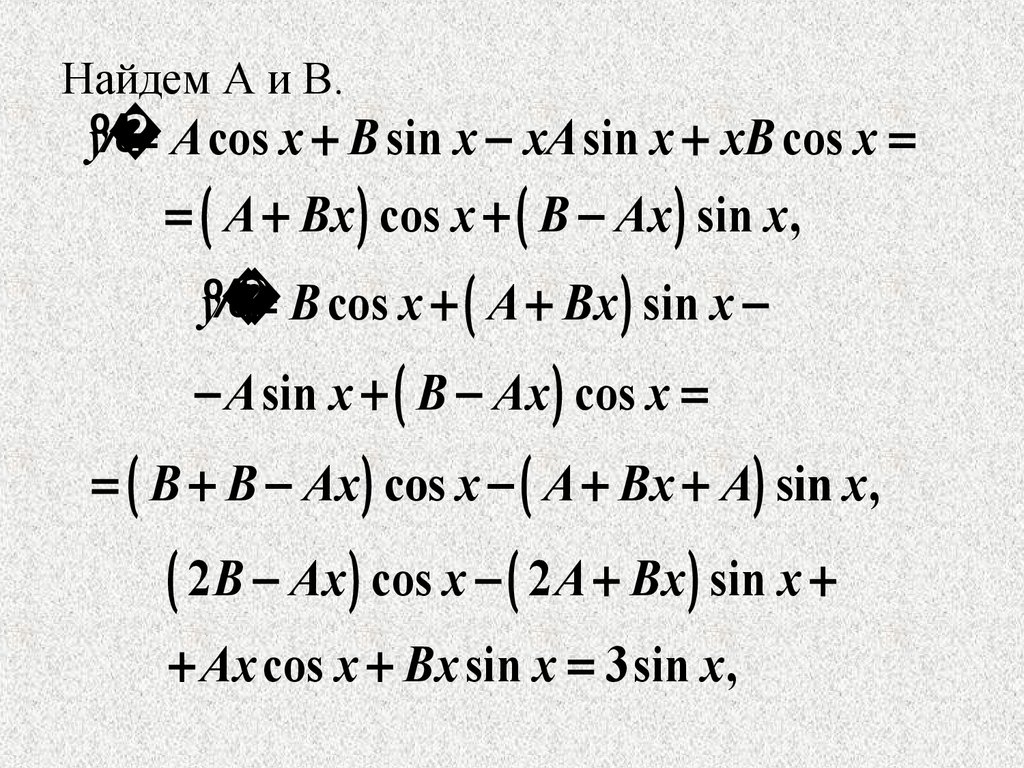






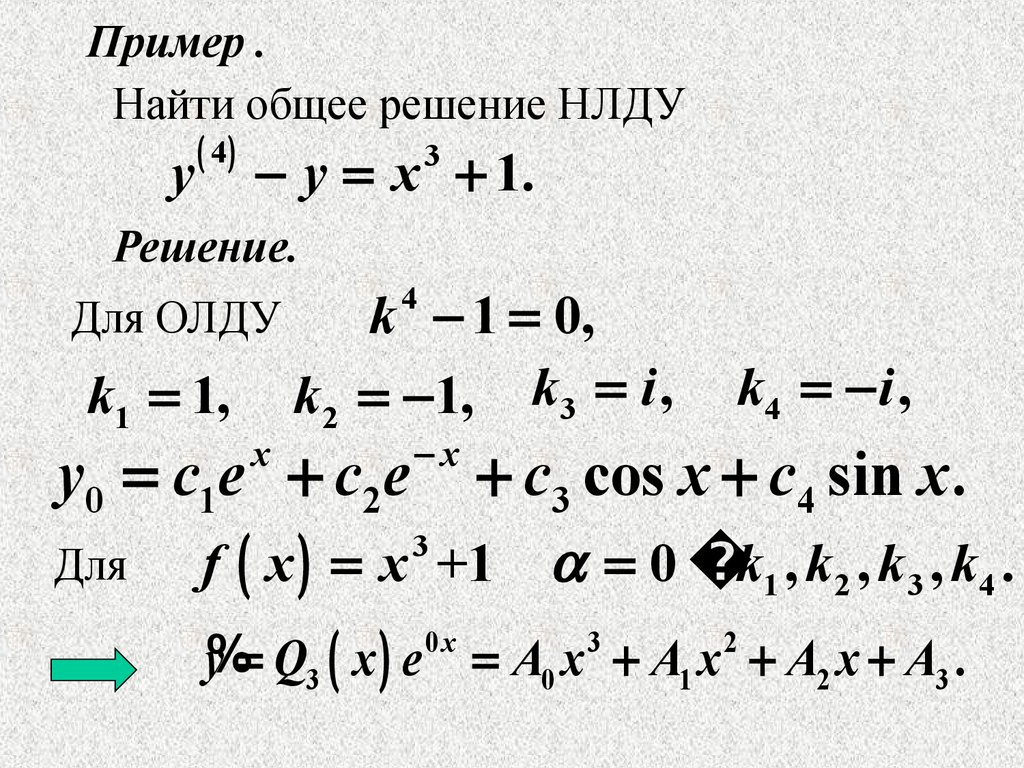

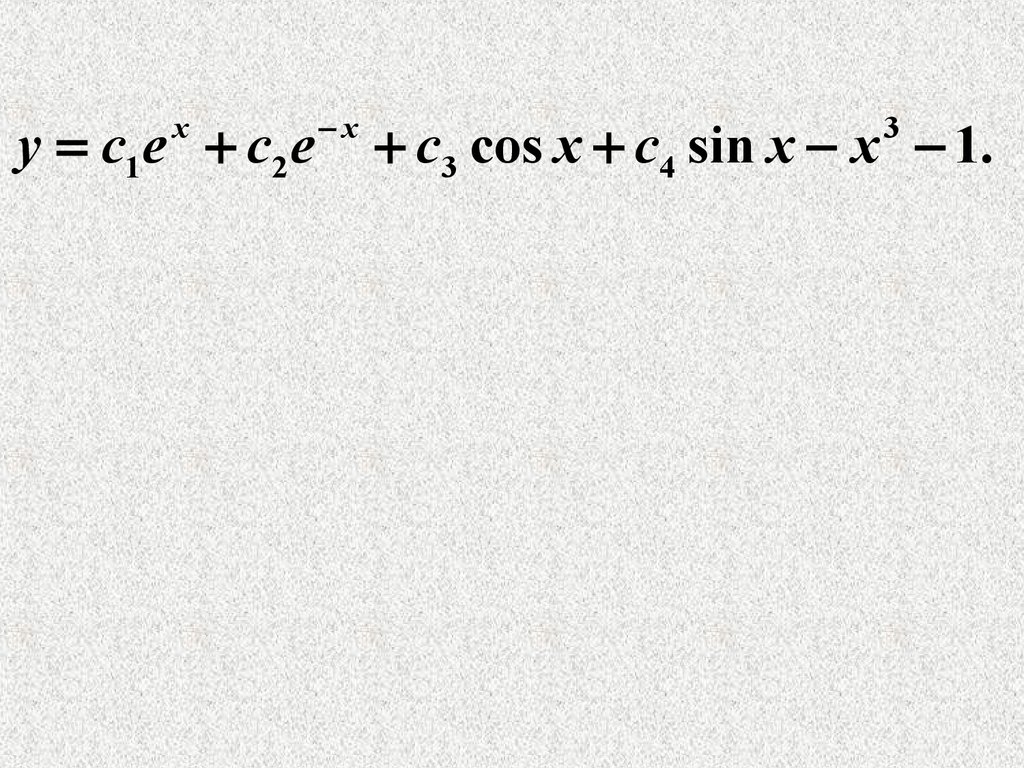



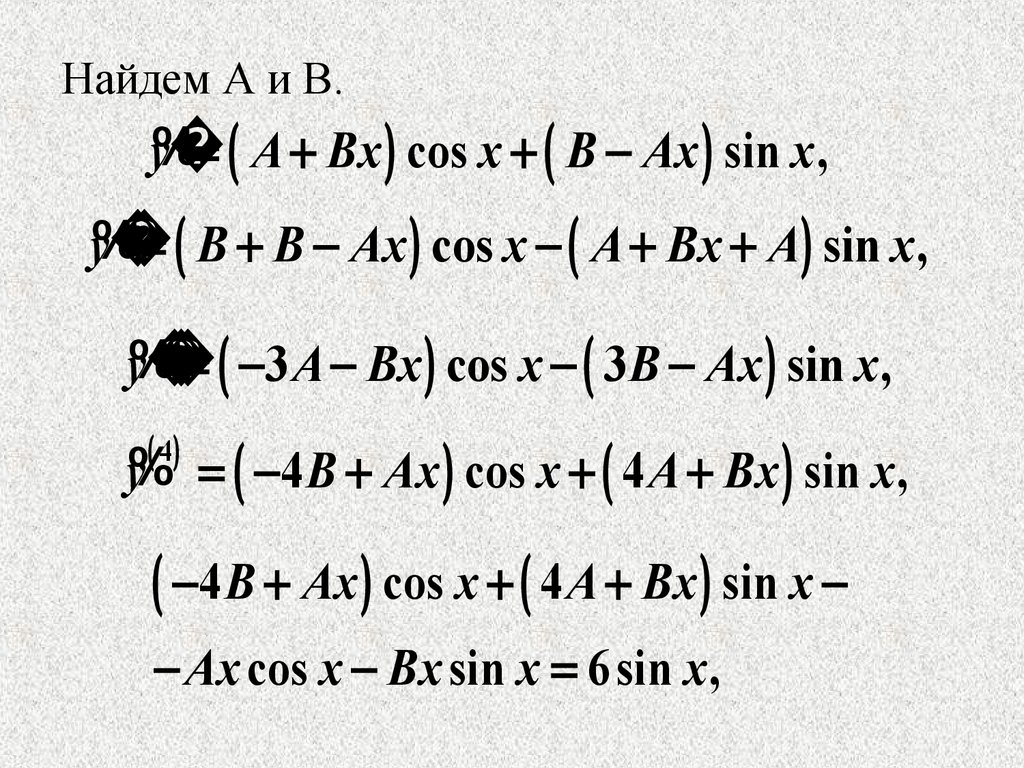
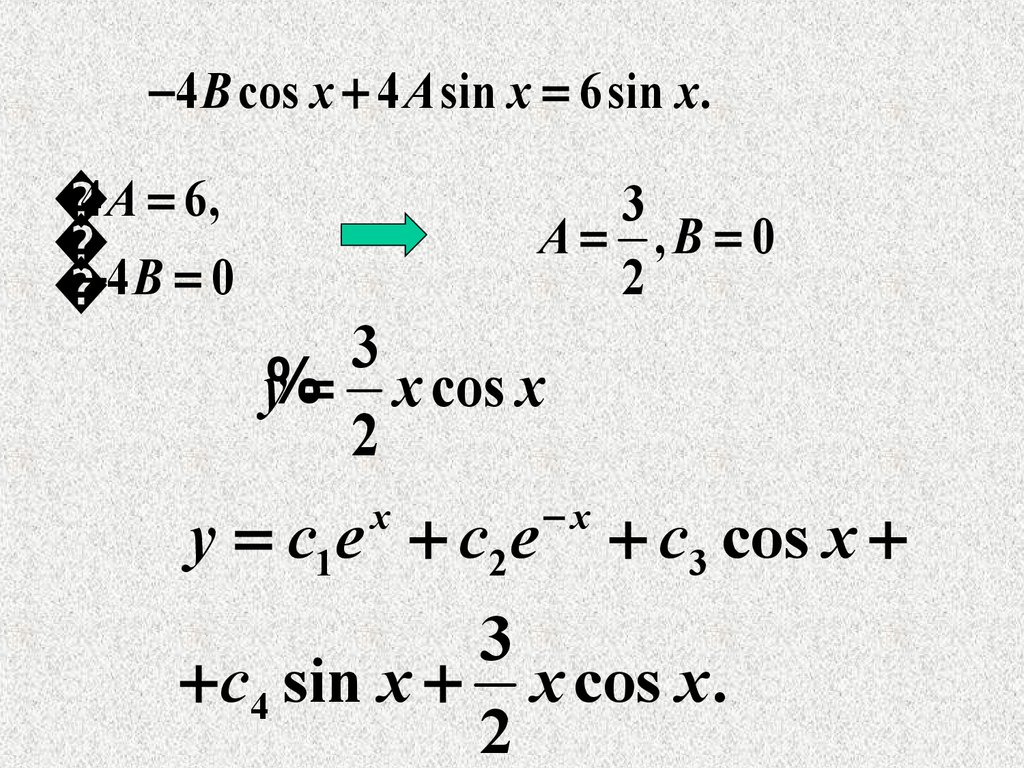







 mathematics
mathematics








