Similar presentations:
Основные законы распределения дисперсных случайных величин
1. II. Основные законы распределения д.с.в.
§1. Биномиальный закон распределения.1.
Опр-е.
С.в. Х имеет биномиальное распределение с параметрами n и р, если
она принимает значения 0,1,…,n с вероятностями
P{ X m} C nm p m q n m ,
где 0 p 1,
Х
0
P{X=m}
n
m 0
q 1 p, m 0,1,..., n.
1
2
qn C n1 pq n 1 C n2 p 2 q n 2
C nm p m q n m 1.
…
n
pn
2. Математическое ожидание и дисперсия с.в., распределенной по биномиальному закону.
2.Математическое ожидание и дисперсия с.в., распределенной по
биномиальному закону.
Теорема. Пусть X Bi (n, p ).
Тогда E(X)=np, D(X)=npq, где q=1-p.
Х- число успехов в n испытаниях Б. с вер. успеха р.
успех,
1, если в i испытании наступил
Xi
неудача.
0, если в i испытании наступила
n
n
Представим Х=Х1+Х2+…+Хn ,
E ( X ) E ( X i ) E ( X i ).
n
n
i 1
i 1
i 1
D ( X ) D ( X i ) D ( X i ).
Хi
Р
0
q
E(Xi)=0*q+1*p=p.
1
p
i 1
n
n
i 1
i 1
E ( X ) E ( X i ) p np.
n
n
i 1
i 1
E ( X ) E ( X i ) p np.
3. .
D(Xi)=E(Xi2)-E2(Xi)= p-p2 = p(1-p) =pq.Xi2
0
1
P
q
p
Представим Х=Х1+Х2+…+Хn ,
D(X)=?
n
n
i 1
i 1
E(Xi2)=p;
n
n
i 1
i 1
E ( X ) E ( X i ) p np.
D ( X ) D ( X i ) pq npq.
4.
Пр.В Петербурге в течении трех дней наблюдается наводнение.
Вероятность того, что в каждый из этих дней уровень воды в Неве
превысит ординар равна 0,8.
С.в. Х- число дней, в кот. был превышен ординар.
a) Каков закон распределения с.в. Х?
б) Составить таблицу распределения с.в. Х.
с) Вычислить E(X) и дисперсию Х.
5.
Решение. n=3, p=0,8 q=0,2;X
0
1
P{X=m} 0,008 0,096
2
3
0,384 0,512
P{X=0}=q3=0,008;
P{X=1}=C31p q2=3*0,8*0,22=0,096;
P{X=2}=C32p2 q1=3*0,82*0,2=0,384;
P{X=3}=р3 =0,512;
E(X)=np=3*0,8=2,4;
D(X)=npq=3*0,8*0,2=0,48;
(n+1)p=4*0,8=3,2; m0=[3,2]=3;
6. §2. Распределение Пуассона
1. Опр.Д.с.в. Х имеет распределение Пуассона с параметром λ>0, если
она принимает значения 0,1,2,…,
а соответствующие им вероятности определяются формулой
m
P{X m}
e ,
m!
2.
m 0,1,2,...
Математическое ожидание и дисперсия с.в., распределенной по закону
Пуассона.
Теорема. Пусть с.в. Х распределена по закону Пуассона с параметром λ.
Тогда E(X)= λ и D(X)= λ.
Док-во.
7. D(X)=E(X2)-E2(X).
mE ( X ) mP{ X m} m
e
m 0
m 0 m!
m
m 1
m
e
e
m 1 m(m 1)!
m 1 (m 1)!
m 1
e
e
e
.
m 1 (m 1)!
D(X)=E(X2)-E2(X).
8.
22
2
2
2
E ( X ) m P{ X m } m P{ X m}
m 1
m 0
2 m
m 1
e
m
e
m
m!
m 1 (m 1)!
m 1
m 1
m 1
e
e
(m 1)
(m 1)!
m 1 (m 1)!
m 1
E ( X ) e e 2 .
D ( X ) 2 2 .






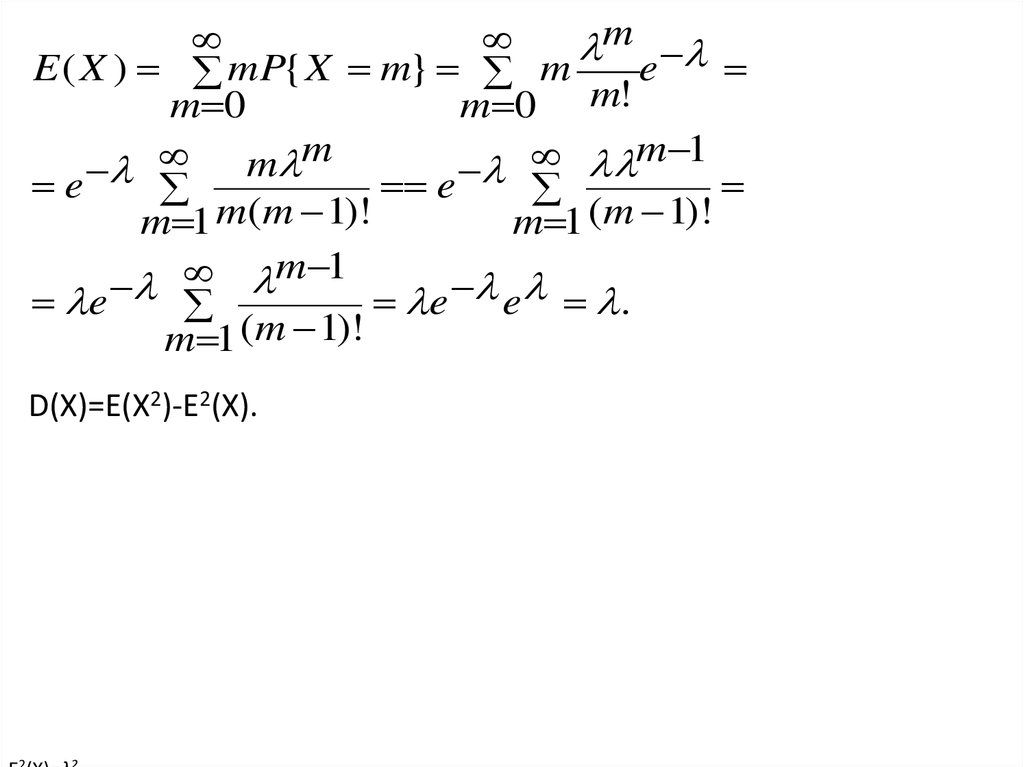
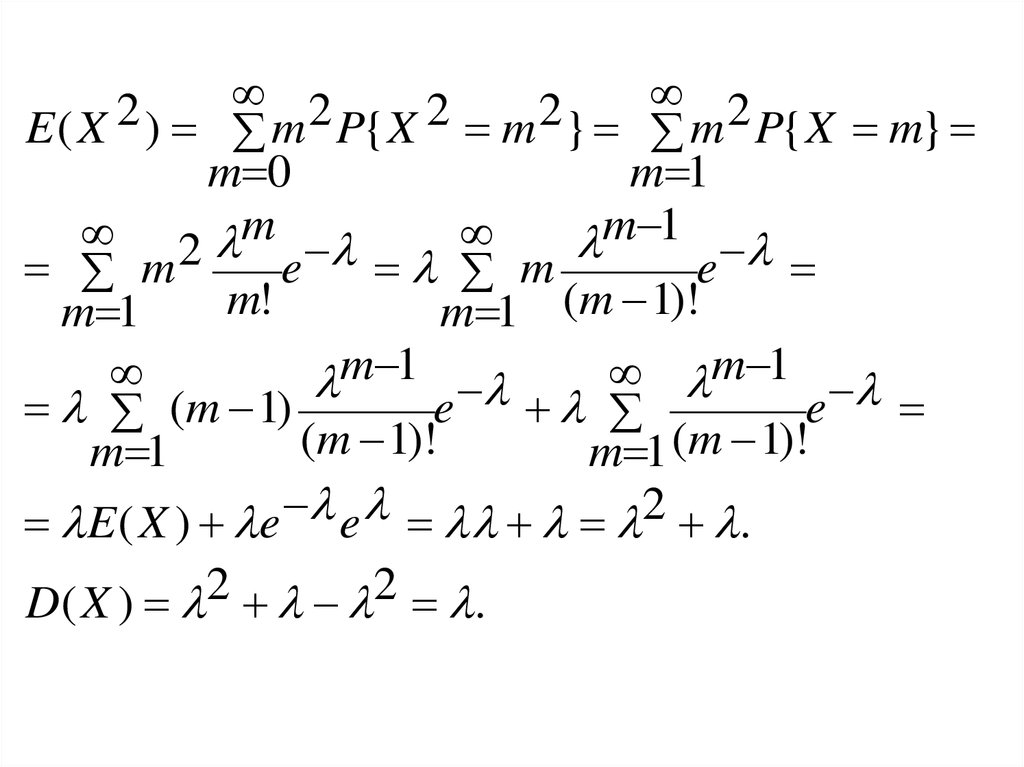


 mathematics
mathematics








