Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем

1. Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем.

Саратовский государственный технический университет
имени Гагарина Ю.А.
Использование метода ЛАЧХ для синтеза
регуляторов манипулятора с гибким стержнем.
Выполнил Скалов Б. Ю
Руководитель работы: к.т.н., доц. Смарунь А.Б.

2. Актуальность работы

• Манипулятор с рабочим органом в виде
вязкоупругого стержня – сложная комбинированная
система, состоящая из сосредоточенных и
распределенных элементов. Для синтеза регулятора
таких систем используются методы параметрической
оптимизации, которые сложны и не наглядны.
• Является актуальным использовать для синтеза
регулятора таких систем хорошо известный
инженерам и наглядный метод логарифмических
амплитудных и фазовых частотных характеристик.

3. Цель работы

• Целью работы является исследование
возможности применения метода
логарифмических амплитудночастотных характеристик для синтеза
регулятора системы управления
манипулятором с упругим стержнем.

4.

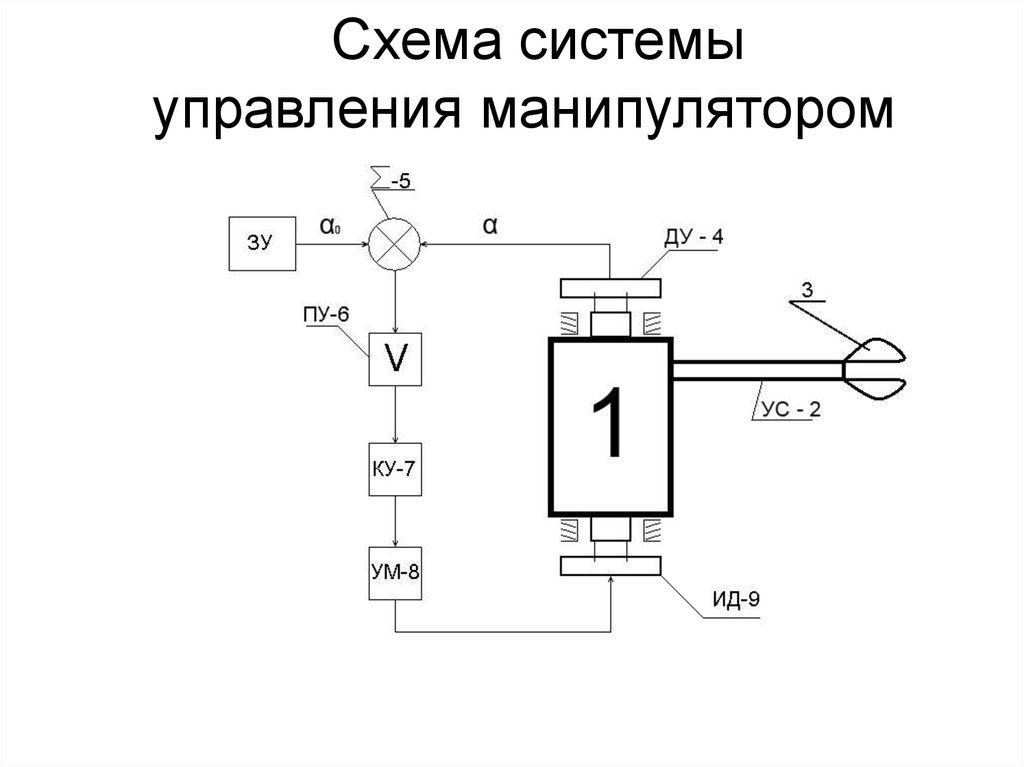
Схема системы
управления манипулятором

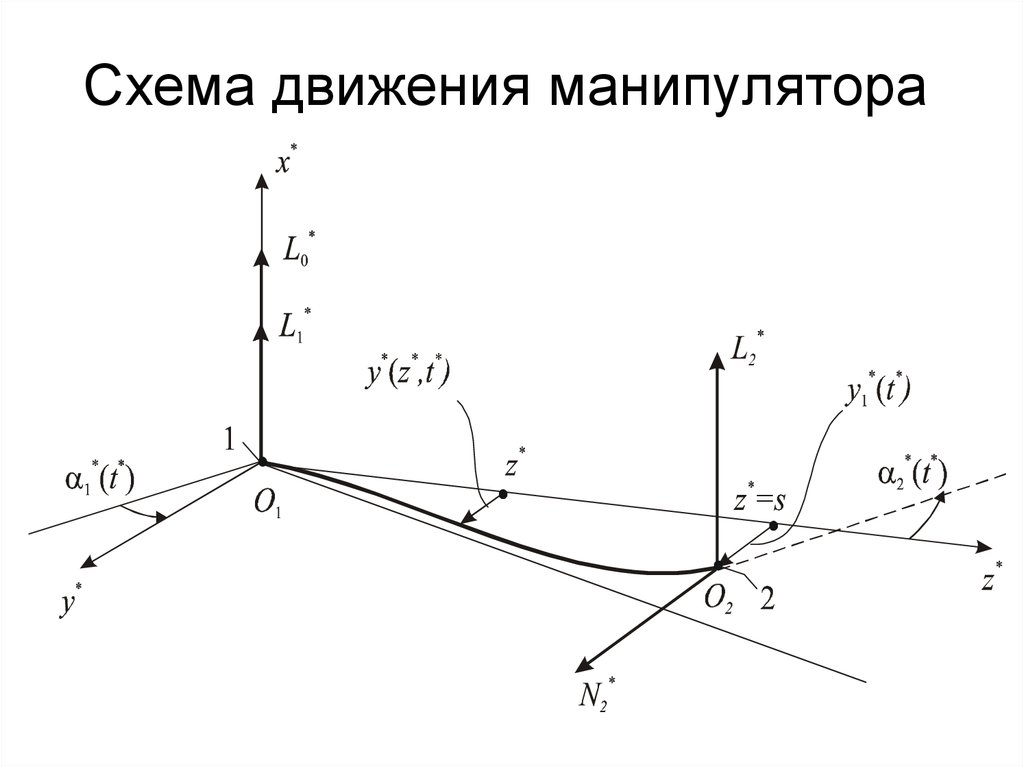
5. Схема движения манипулятора

6. Уравнения движения манипулятора в размерной форме

Уравнение углового движения абсолютно жесткого вала
*
*
*
* *
*
J 1 0 1 k0 1 L1 ,
*
0
Уравнение углового движения исполнительного органа манипулятора
J 2* ( 1* 2* ) L*2
Уравнение линейного перемещения исполнительного органа
m2* ( y 1* s 1 ) N 2* ,
Уравнение изгиба тонкого стержня
1* ) EJ (1 h
( y * ( z * ,t * ) z *
д * * *
д
)
y
(
z
,
t
)
,
(
)
дt *
дz *

7. Уравнения движения манипулятора в размерной форме

Задаем граничные условия
z * 0: y * (0,t * ) 0 , y * (0,t * ) 0
z * s : y * (s,t * ) y (t * ), y * (s,t * ) * (t * )
1
2
и прогиб стержня в начальный момент времени
t* 0 :
1* (0) 0 , 1* (0) 0 , 2* (0) 0 , 2* (0) 0
y1 (0) 0, y 1 (0) 0, y* ( z* ,0) 0, y * ( z* ,0) 0
Уравнения связи
д
д
L*1 EJ 1 h * y* (0,t * ), L*2 EJ 1 h * y* (s,t * )
дt
дt
д
N 2* EJ 1 h * y* ( s,t * )
дt

8. Приведение уравнений к безразмерной форме

Известно , что в гибких стержнях характерные процессы определяются
такими параметрами стержней и их материала:
E – модуль Юнга упругости материала;
J – момент инерции поперечного сечения стержня;
s – длина стержня;
ρ – плотность материала стержня.
Их этих параметров можно составить комбинацию имеющую
размерность времени
s
T
EJ
4
1
2
Эта комбинация представляет собой характерное
время протекающих в стержнях процессов

9. Приведение уравнений к безразмерной форме

Имея единый масштаб длины можно ввести безразмерные переменные
y1 =y1*/ , y1- безразмерное упругое перемещение конца стержня;
y =y*/ , y – безразмерный прогиб стержня;
z=z*/ s, z – безразмерная координата поперечного сечения стержня.
0 / ,
s
*
0
1 / ,
s
J 0 J 0* /( s 3 ),
L1 L*1/L
*
1
1
s
2 / ,
s
*
2
J 2 J 2* /( s 3 ), m2 m2* /( s ), k0 k0*
L2 L*2 /L,
L
EJ
*
,
N
N
/N ,
2
2
2
s
N
EJT
,
s
EJ
,
3
s
hT

10. Уравнения движения манипулятора в безразмерной форме

Обыкновенные дифференциальные уравнения движения абсолютно твердых
вала и исполнительного органа.
J 0 1 1 k0 1 L1 0 , J 2 ( 1 2 ) L2 0
1 ) N2 0
1 y1 , m2 ( y 1
Дифференциальное уравнение с частными
моделирующее процессы изгиба стержня.
производными,
д
д
1 , ( )
y 1 y z
дt
дz
Граничные условия.
Начальные условия.
z 0 : y (0, t ) 0 , y (0, t ) 0
1 (0) 2 (0)
2 (0)
t 0: 1 (0)
y1 (0) y 1 (0) y( z,0) y ( z,0) 0
z 1: y(1, t ) y1 (t ) , y (1, t ) 2
Уравнения связи абсолютно твердых вала и исполнительного органа через гибкий стержень.
д
д
L1 1 y (0,t ) , L2 1 y (1,t )
дt
дt
д
N 2 1 y (1,t )
дt

11. Уравнения системы управления манипулятором в изображениях

( J 0 2 k 0 ( ) p) 1 ( ) L1 ( ) p 0 ( )
m2 2 ( y1 ( ) 1 ( )) N 2 ( ) 0,
J 2 2 ( 1 ( ) 2 ( )) L2 ( ) 0
( ) 1 ( ) y1 ( ),
4
4
y ( z, ) k y( z, ) k z 1 ( ) ,
z 0 : y (0, ) 0, y (0, ) 0
П ( ) A( )
B ( )
2
k
1
4
z 1 : y(1, ) y1 ( ), y (1, ) a2 ( )
L1 ( ) 1 y (0, ), L2 ( ) 1 y (1, )
N2 ( ) 1 y (1, )
Здесь 0( ), 1( ), 2( ), y1( ), y(z, ) L1( ), L2( ), N2( ) – изображения соответствующих оригиналов;
A( ) и B( ) – многочлены; П( ) – рациональная дробь; – произвольный комплексный параметр.
Выберем характерный прогиб стержня используя методы теории упругости.
Согласно этой теории в стержне будут отсутствовать пластические деформации, если его характерный
прогиб удовлетворяет условию
s 2 3
s 2 3
принимаем d 10 [ м] ,где d - характерный диаметральный размер
10 [ м] ; поэтому
поперечного сечения стержня в направлении изгиба.
d

12. Передаточные функции замкнутой и разомкнутой систем стабилизации манипулятора

Структурная схема системы стабилизации манипулятора с регулятором самого
общего вида
передаточная функция замкнутой
системы управления
передаточная функция разомкнутой
системы управления

13. Синтез регулятора для системы управления манипулятором по методу ЛАЧХ

ЛАХ
ФЧХ

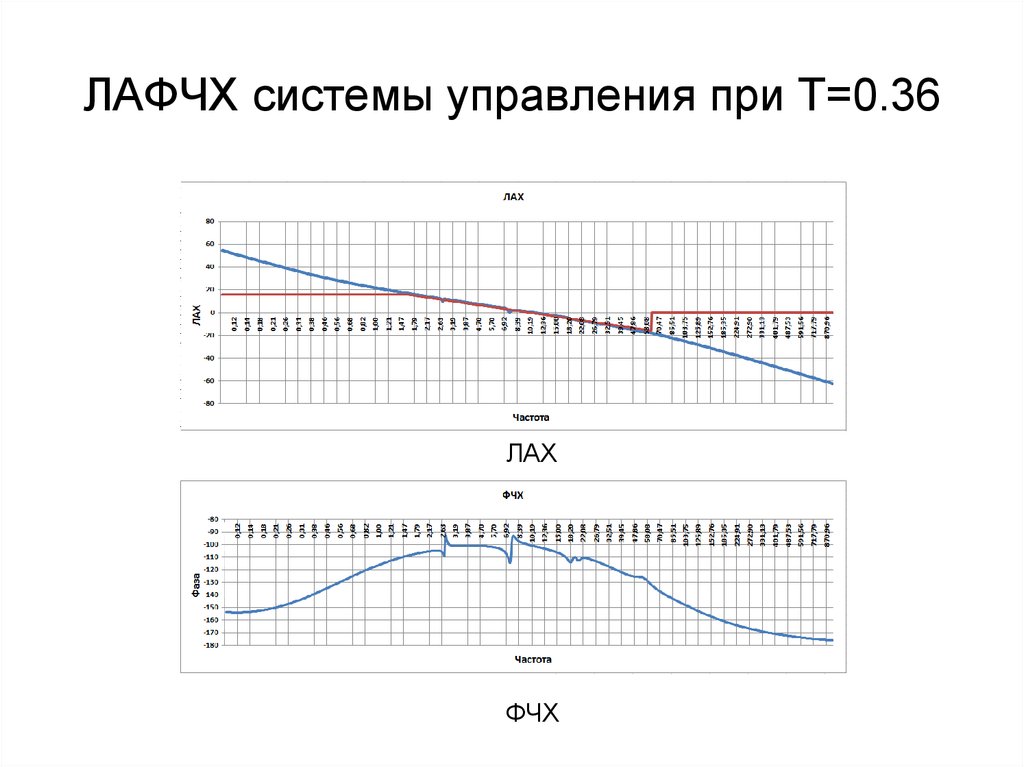
14. ЛАФЧХ системы управления при T=0.36

ЛАХ
ФЧХ

15. Амплитудная частотная характеристика замкнутой системы

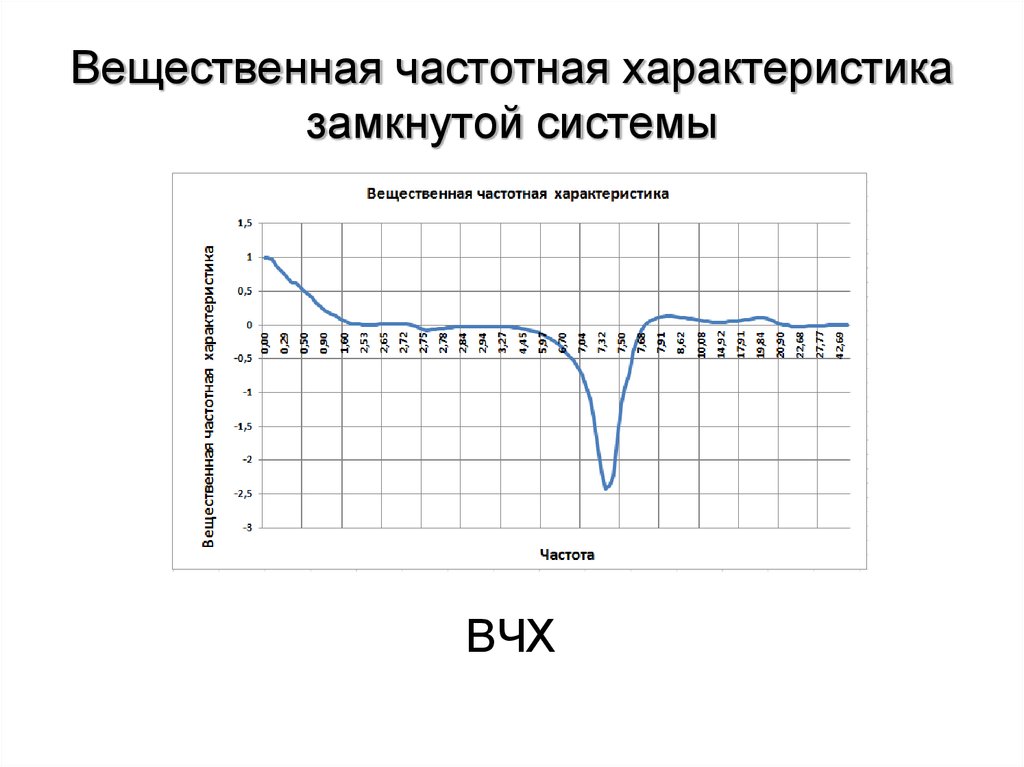
АЧХ

16. Вещественная частотная характеристика замкнутой системы

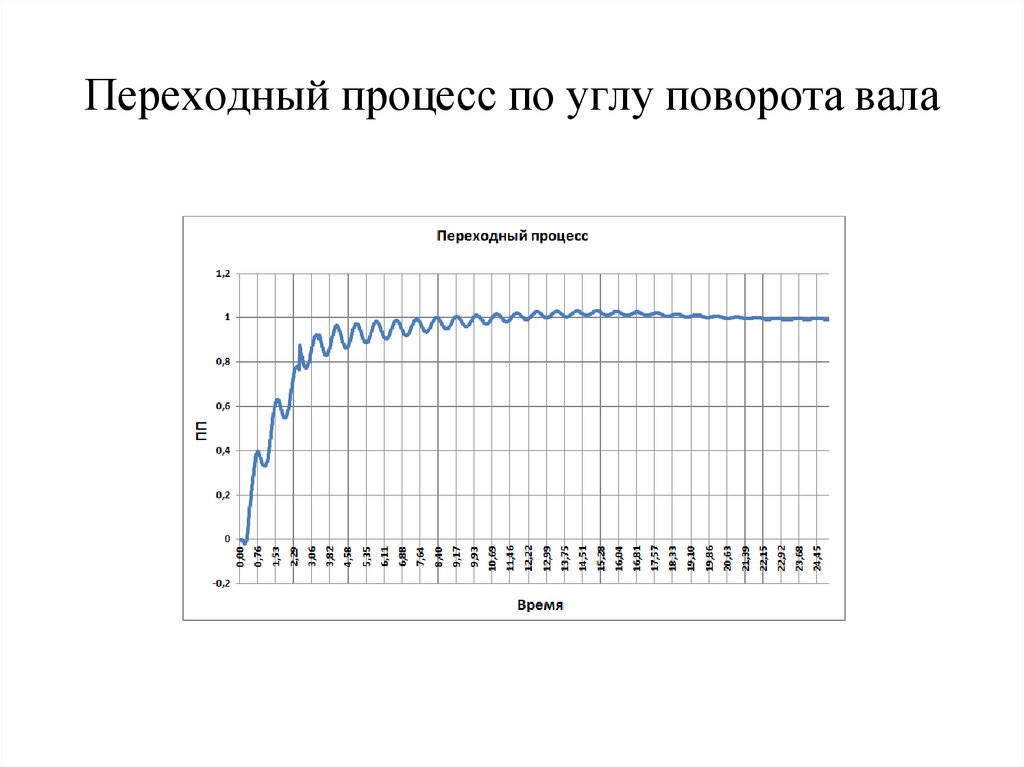
ВЧХ

17. Переходный процесс по углу поворота вала

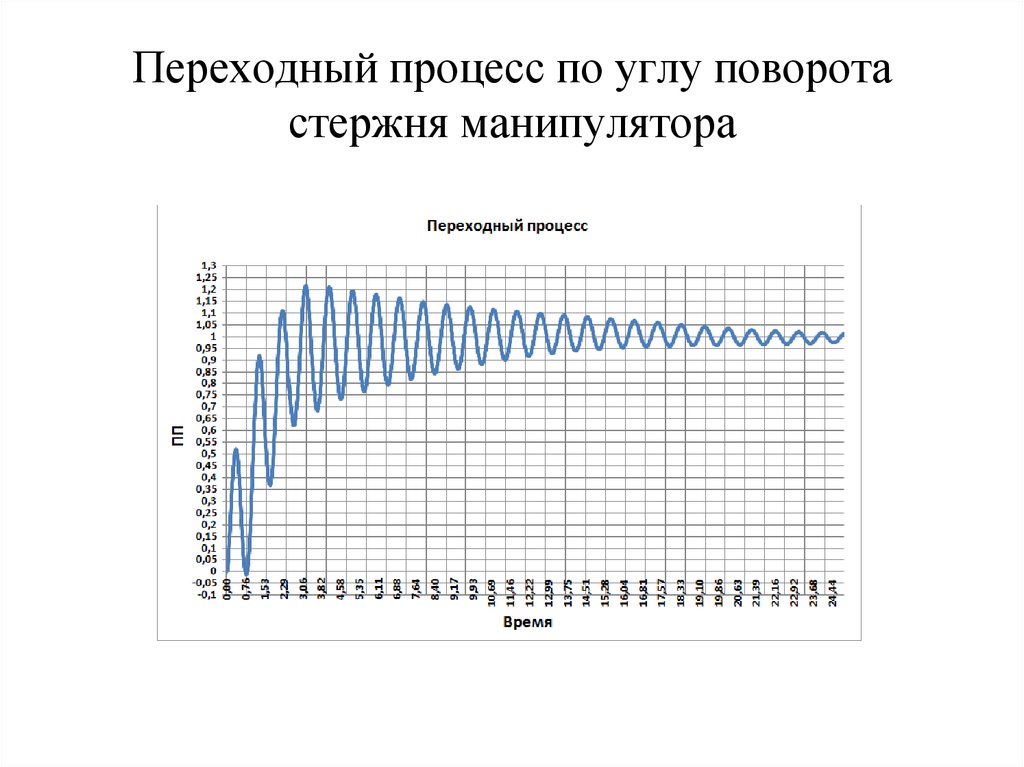
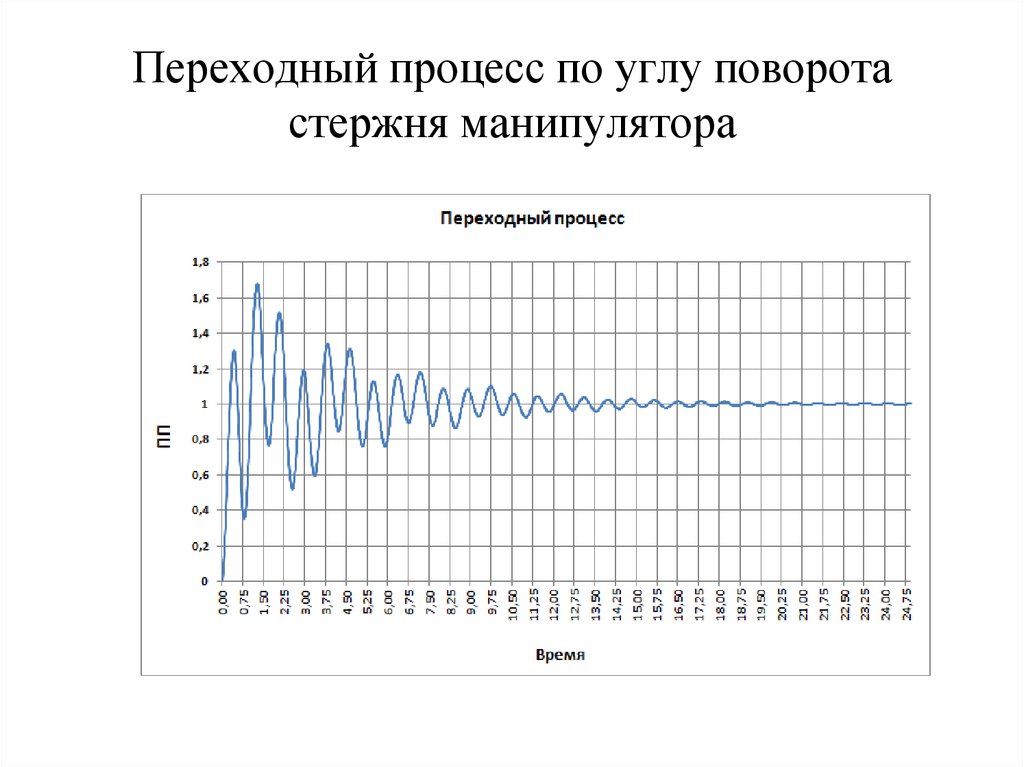
18. Переходный процесс по углу поворота стержня манипулятора

19. Исследование устойчивости системы управления манипулятором по критерию Михайлова

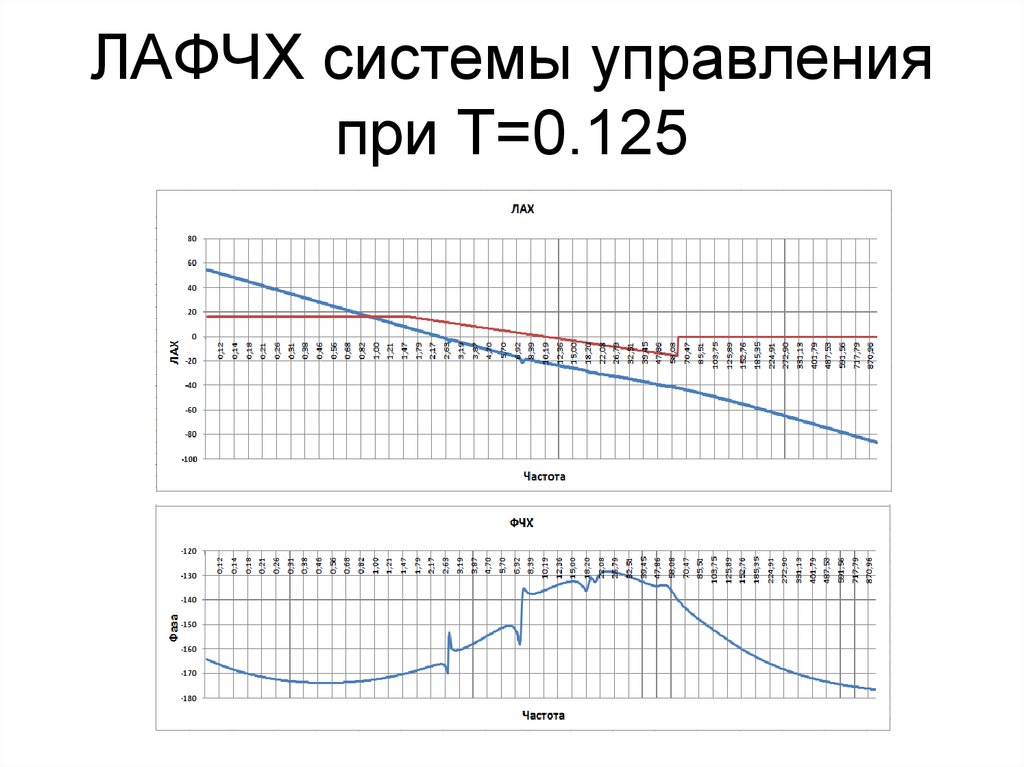
20. ЛАФЧХ системы управления при T=0.125

21. Амплитудная частотная характеристика замкнутой системы

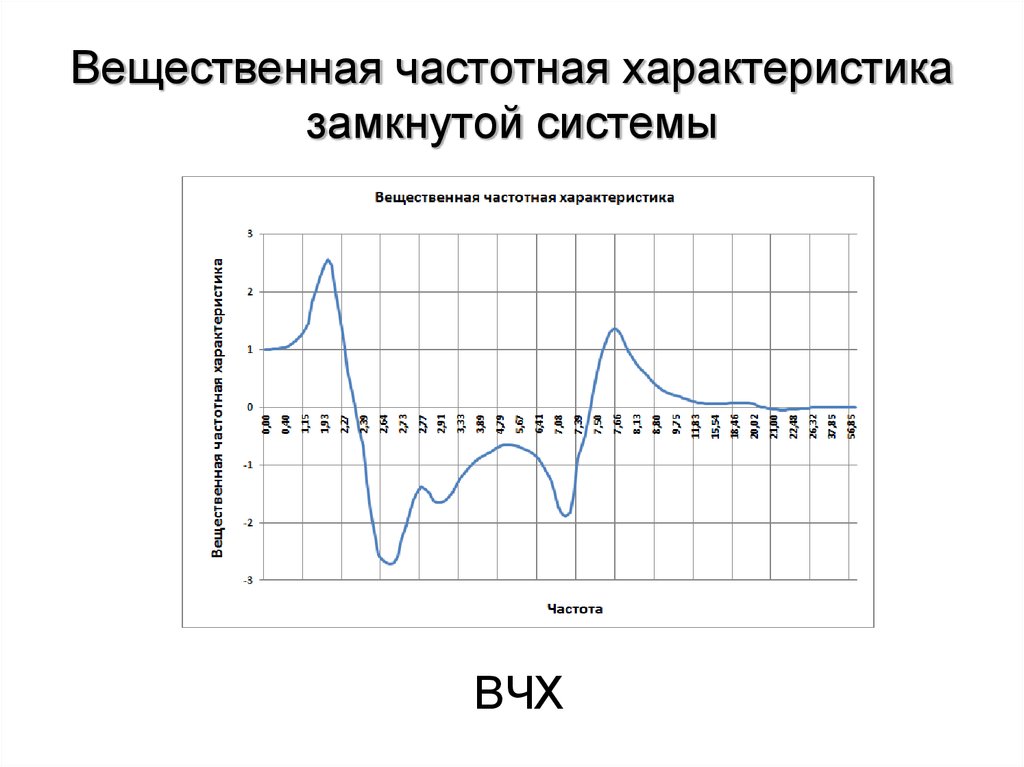
АЧХ

22. Вещественная частотная характеристика замкнутой системы

ВЧХ

23. Переходный процесс по углу поворота вала

24. Переходный процесс по углу поворота стержня манипулятора

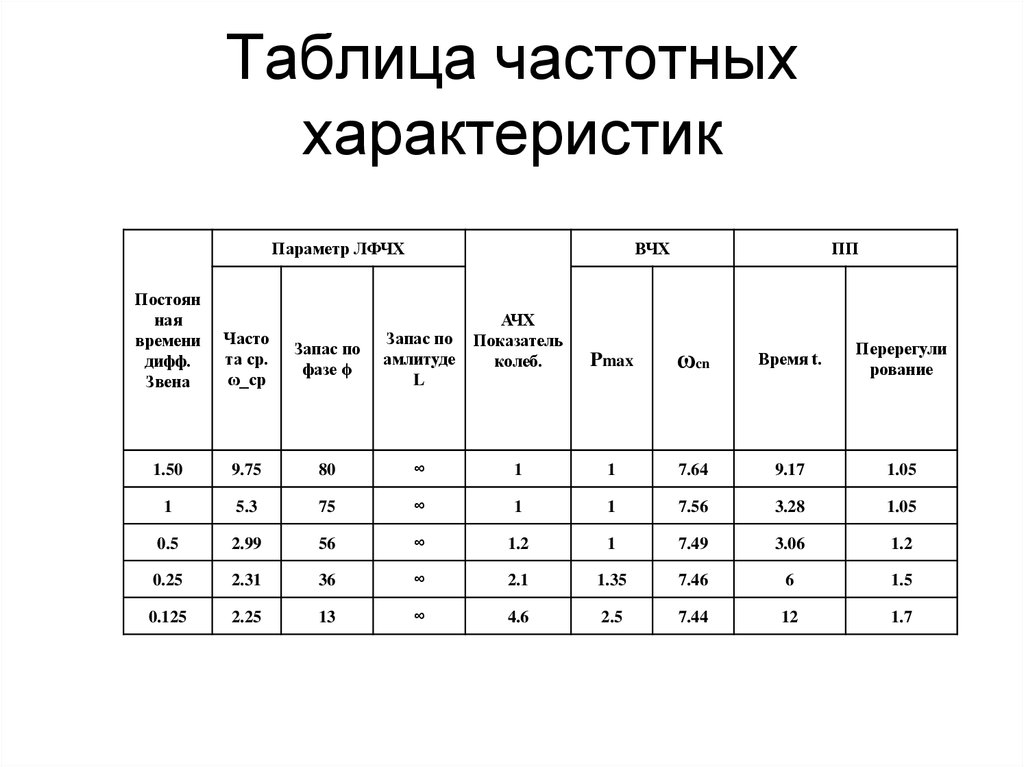
25. Таблица частотных характеристик

Параметр ЛФЧХ
ВЧХ
Постоян
ная
времени
дифф.
Звена
Часто
та ср.
ω_ср
Запас по
фазе ϕ
Запас по
амлитуде
L
1.50
9.75
80
1
5.3
0.5
ПП
АЧХ
Показатель
колеб.
Pmax
ωcn
Время t.
Перерегули
рование
∞
1
1
7.64
9.17
1.05
75
∞
1
1
7.56
3.28
1.05
2.99
56
∞
1.2
1
7.49
3.06
1.2
0.25
2.31
36
∞
2.1
1.35
7.46
6
1.5
0.125
2.25
13
∞
4.6
2.5
7.44
12
1.7

26. ЗАКЛЮЧЕНИЕ

СФОРМУЛИРУЕМ ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ ПО ВЫПУСКНОЙ
КВАЛИФИКАЦИОННОЙ РАБОТЕ:
1. Разработаны размерная и безразмерная математические модели системы
управления манипулятора с рабочим инструментом в виде вязкоупругого
стержня.
2. Сформирована структурная схема системы управления плоским движением
манипулятора с вязкоупругим стержнем. Получены передаточные функции
разомкнутой и замкнутой систем управления манипулятором.
3. Методом логарифмических амплитудных и фазовых частотных характеристик
получены корректирующие устройства для системы управления плоским
движением манипулятора с вязкоупругим стержнем, для разных значений
частотных показателей качества управления.
4. Показано, что для системы управления манипулятора с рабочим
инструментом в виде вязкоупругого стержня для получения приемлемых
показателей переходных процессов требуются более высокие частотные
показатели качеств по сравнению с системами с сосредоточенными
параметрами.

27. СПАСИБО ЗА ВНИМАНИЕ