Similar presentations:
Уравнения с параметрами
1. Применение МСИ при изучении темы «Уравнения с параметрами»
Крючкова И.Я.,учитель математики
МОУ СОШ88
г.Ярославля
2.
• В структуру КИМ по математике включенызадания части С, без решения которых
невозможно получить высокий результат.
• Поэтому, начиная с 8 класса, необходима
планомерная работа по развитию
соответствующих качеств ума,
сообразительности, творческих и
аналитических
3.
• Задачи с параметрами представляютсложность в техническом и логически,
поэтому умение решать их предопределяет
успешность при сдаче экзаменов в любом
ВУЗе России
4.
• Задачи с параметрами формируют умениевидеть причинно-следственные связи,
решать многоуровневые задачи ,
развивают логику, мышление,
сообразительность.
• Большинство заданий с параметрами
охватывает узкий круг вопросов и делает в
основном упор на рецептуру, а не логику
решения задач.
5.
• Т.К. многие задачи без ответа решитьбывает тяжело, необходимо определить
метод быстрой проверки решения
6. Калькуляторы
• Для быстрой и достоверной проверкиответа применяем «калькулятор CASIO»
7.
• Решение уравнений с параметрамивызывают в старших классах большие
затруднения, однако это задание С5 в ЕГЭ
по математике, правильное решение
которого оценивается в 4 балла. Чтобы
сформировать навык их решения имеет
смысл начинать работу с уравнениями с
параметрами в среднем звене.
8. Определите при каком значении параметра А уравнение у=x2+Ax+A имеет один корень?
• Важно, чтобы обучающиеся понимали, чтоизменяя значение параметра А мы
получаем семейство парабол, из которого
нам нужно выбрать ту, которая
удовлетворяет условию задания.
9.
10. Калькулятор позволяет практически мгновенно построить графики функций при различных А и проверить правильность аналитического решения ч
Калькулятор позволяет практически мгновенно построить графикифункций при различных А и проверить правильность
аналитического решения через нахождение дискриминанта.
Одно решение данное уравнение имеет при А=0 и А=4
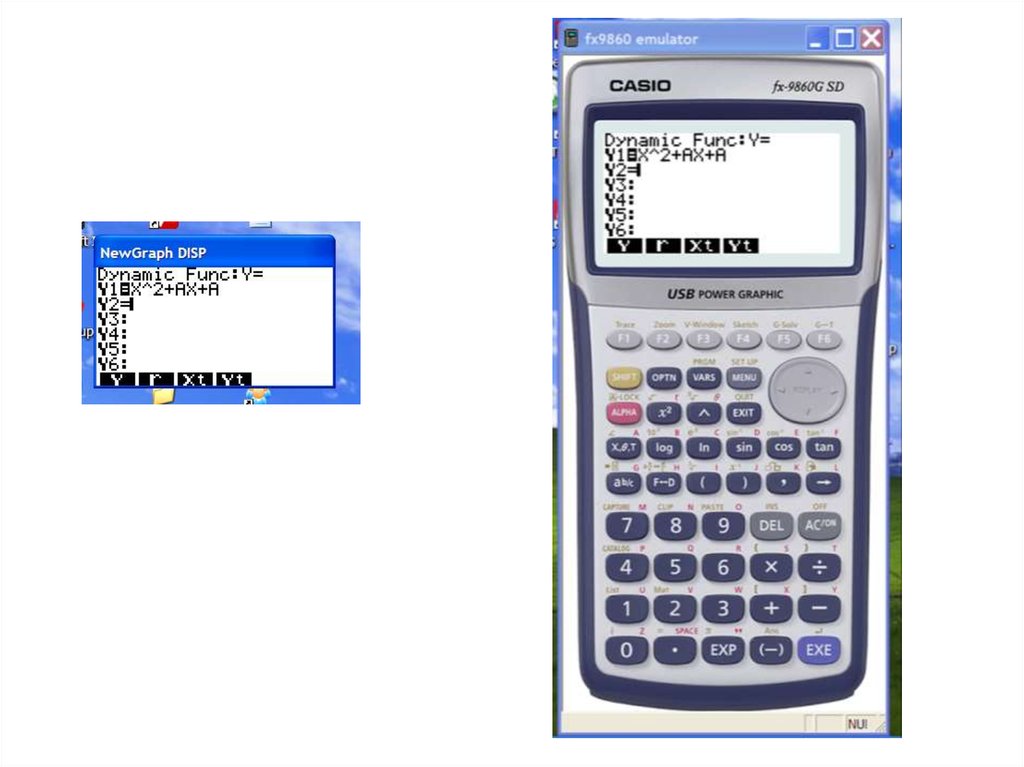
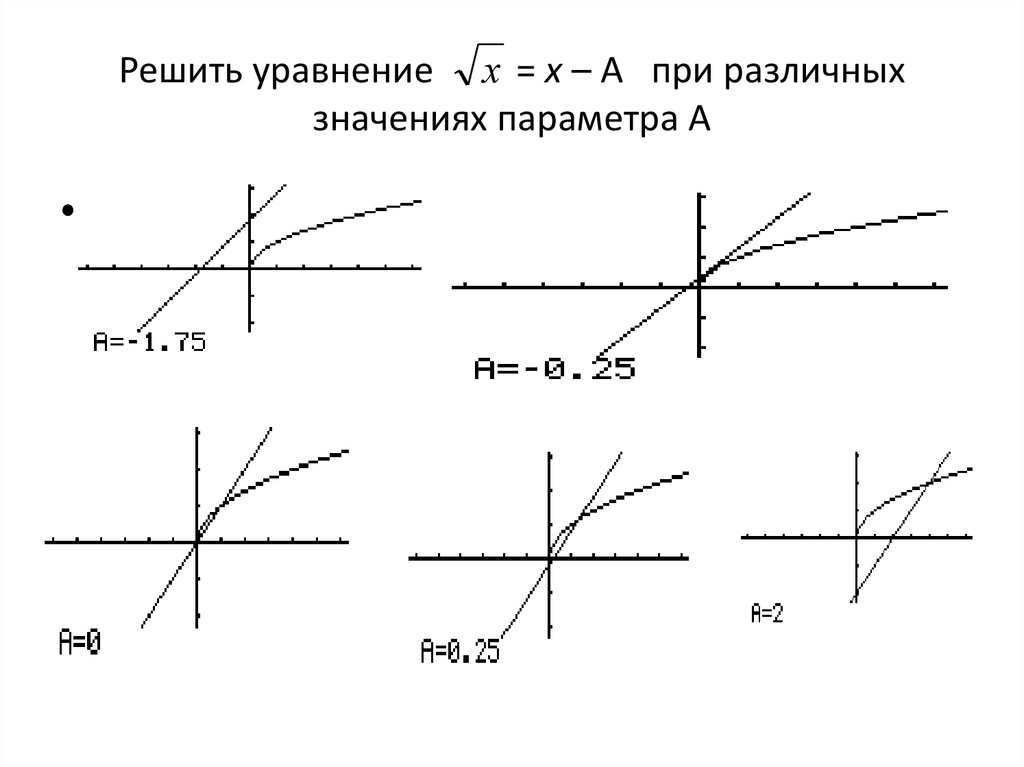
11. Решить уравнение = х – A при различных значениях параметра А
Решить уравнение х = х – A при различныхзначениях параметра А
12.
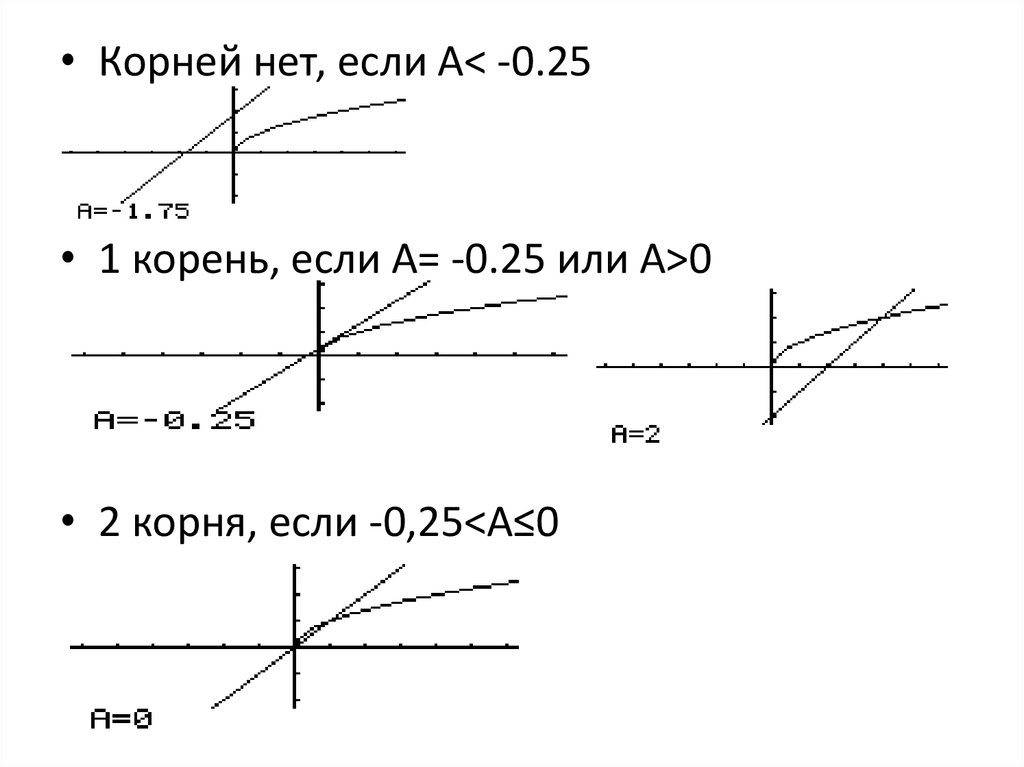
• Корней нет, если А< -0.25• 1 корень, если А= -0.25 или А>0
• 2 корня, если -0,25<A≤0
13.
• В 8 классе решаются уравнения видах =кх+в графически, аналитическое решение
возможно, но это задание повышенной
сложности. Использование калькулятора
позволяет быстро проверить выполненное
решение
• В 11 классе решение данного уравнения с
помощью производной или путем возведения
правой и левой частей уравнения в квадрат.
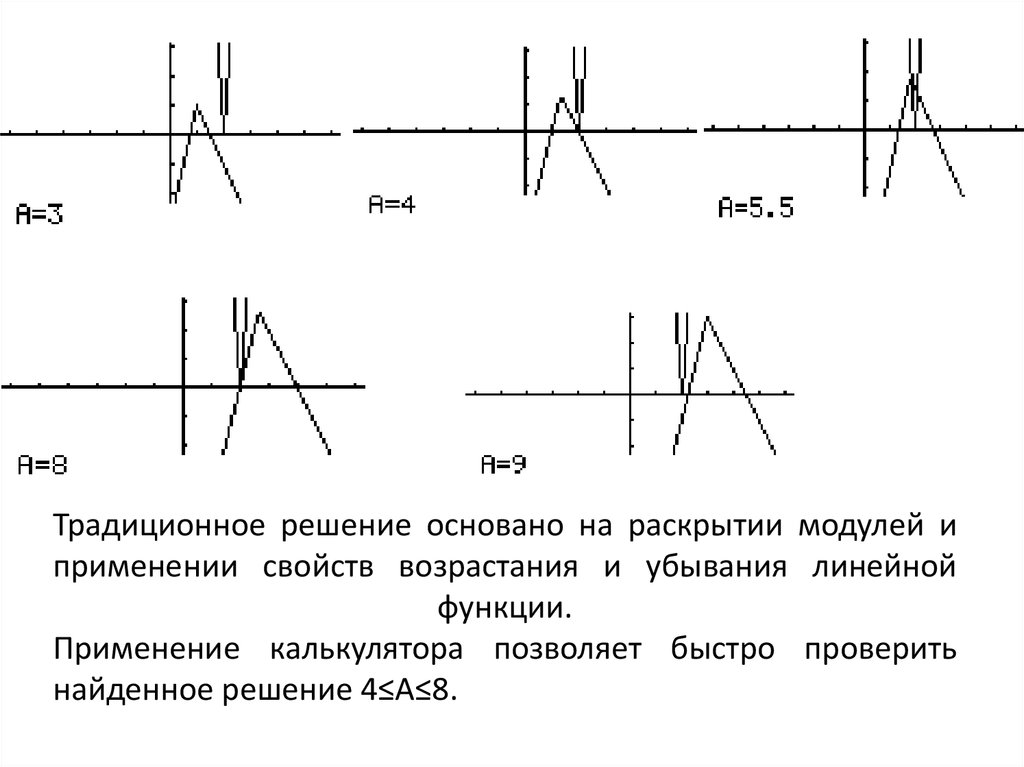
14. Найдите все значения параметра А, при которых уравнение 5х-|4х+|3х-А||=13|х-2| имеет хотя бы 1 корень
15. Традиционное решение основано на раскрытии модулей и применении свойств возрастания и убывания линейной функции. Применение калькулятор
Традиционное решение основано на раскрытии модулей иприменении свойств возрастания и убывания линейной
функции.
Применение калькулятора позволяет быстро проверить
найденное решение 4≤А≤8.
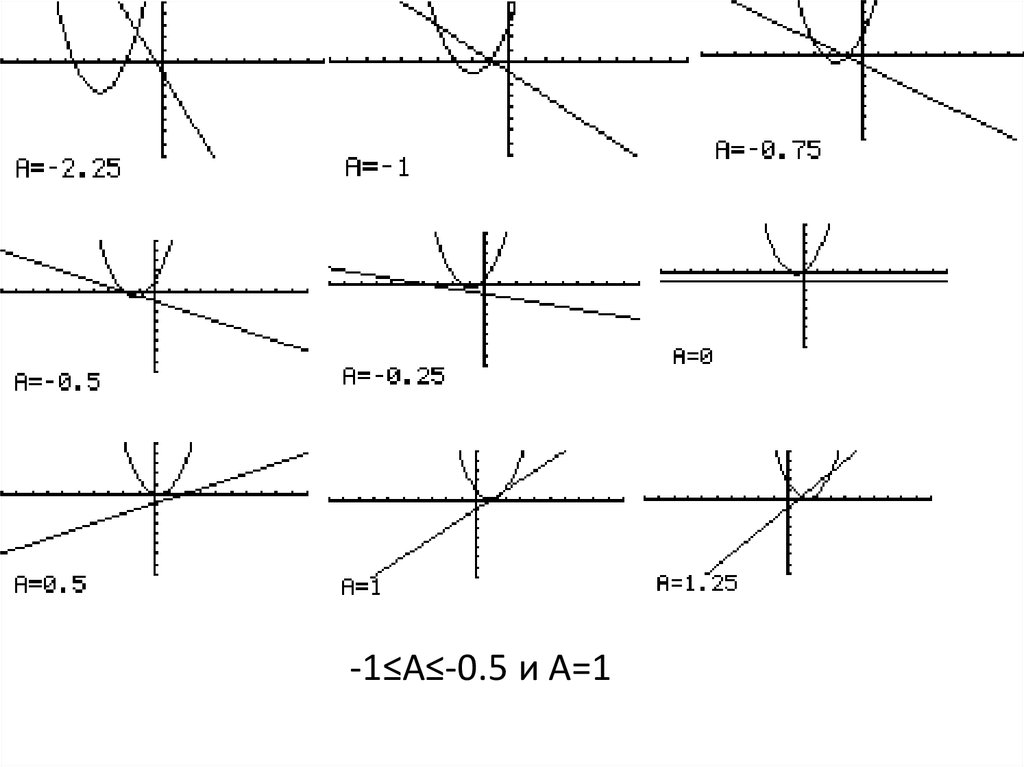
16. Найдите все значения параметра А, при которых система уравнений имеет более 4 решений { х2+(у-А)2=А2 |х2-3|=у
17. -1≤А≤-0.5 и А=1
18.
• Калькуляторы CASIO служат для отработкирешения определенных типов задач, в
которых можно пропустить промежуточный
этап решения и получить быстрый ответ
или проверить уже полученный при
аналитическом решении результат.













 mathematics
mathematics








