Similar presentations:
Решение уравнений, систем уравнений с параметрами графическим способом
1. Решение уравнений, систем уравнений с параметрами графическим способом. ГБОУ СОШ №249 Теплякова Л.Ф.
2. Эпиграф
Если вы хотите научитьсяплавать, то смело входите в
воду, а если хотите
научиться решать задачи –
решайте их.
Д. Пойа “Математическое открытие”
3.
• Переменные a, b, c, ..., которыепри решении уравнения считаются
постоянными, называются
параметрами,
а само уравнение называется
уравнением, содержащим
параметры.
• Параметры обозначаются первыми
буквами латинского алфавита: a,
b, c, d, ..., а неизвестные - буквами
x, y, z.
4.
• Решитьуравнение
с
параметрами - значит указать,
при
каких
значениях
параметров
существуют
решения и каковы они.
• Существует
несколько
алгоритмов решения уравнений
с параметрами.
5. Аналитический способ решения.
Является наиболее сложным способомрешения выражений с параметром.
Требует точное знание таких понятий
как область определения,
равносильность, тождественность,
следствие, а также теорем связанных с
этими понятиями. В ЕГЭ представлены
варианты которые возможно решить
наиболее простым способом.
6.
Алгоритм решения уравнений спараметром графическим способом.
1. Находим область определения.
2. Переносим выражение содержащее a
в правую часть.
3. В системе координат строим графики
для левой и правой части для тех
значений х, которые входят в область
определения данного уравнения
(неравенства).
4.Находим точки пересечения графиков
функций, определяем абсциссы точек
пересечения. Для этого достаточно
решить уравнение относительно х.
4. Записываем ответ.
7.
Для успешного решения задач типа С5необходимо:
Уметь решать рациональные,
иррациональные, показательные,
тригонометрические и
логарифмические уравнения, их
системы
Уметь строить графики изученных
функций
Использовать для приближенного
решения графический метод
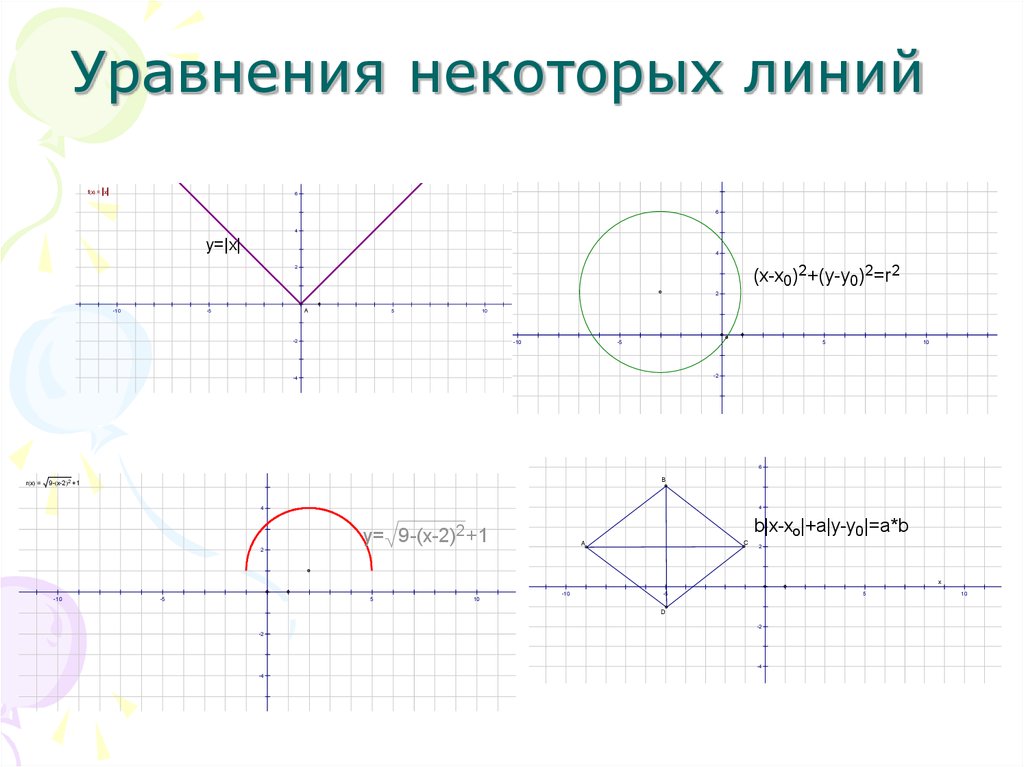
8. Уравнения некоторых линий
f x = x6
6
4
y=|x|
4
(х-х0)2+(у-у0)2=r2
2
2
-10
A
-5
5
10
-2
-10
-5
5
10
-2
-4
6
r x =
B
9- x-2 2 +1
4
4
b|x-xo|+a|y-y0|=a*b
y= 9-(x-2)2 +1
C
A
2
2
x
-10
-10
-5
5
-5
5
10
D
-2
-2
-4
-4
10
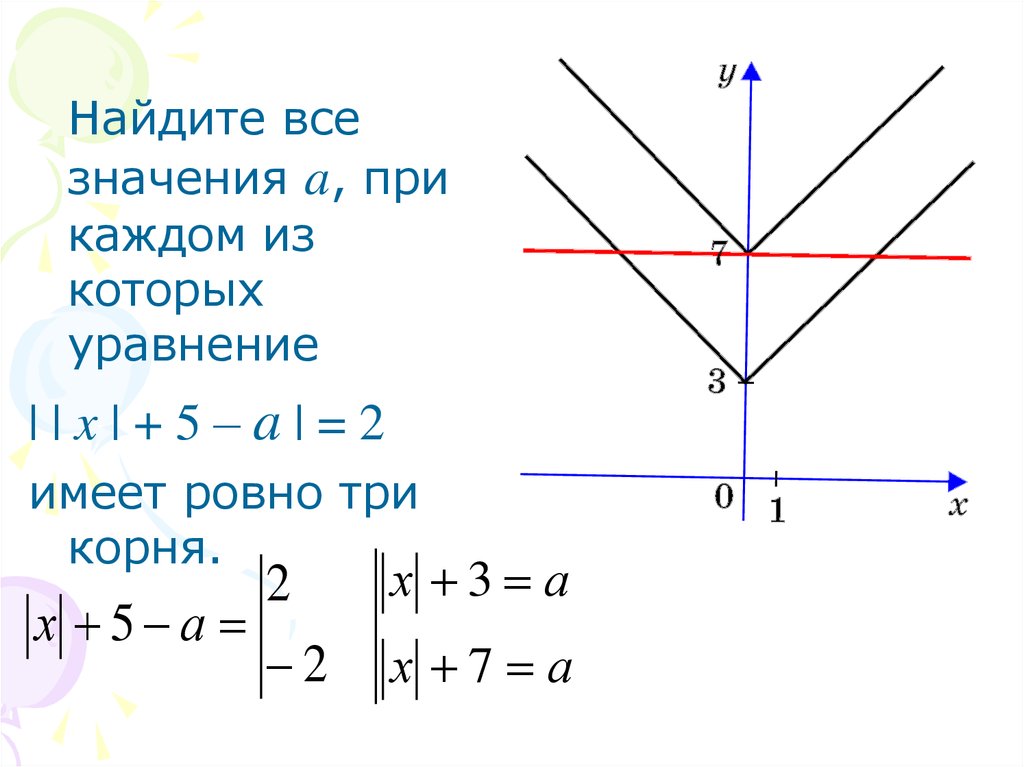
9.
Найдите всезначения a, при
каждом из
которых
уравнение
||x|+5–a|=2
имеет ровно три
корня.
х 5 а
2
х 3 а
2
х 7 а
10.
a11. Рассмотрим неравенство
12.
D2
2
4 a(3a 1) 4 3a a (3a a 4)
4
(3a a 4) <0
2
3a a 4 >0
2
1
1 1 48
a
1
6
1
3
13. Условие: а > 0
Условие: а > 014.
Найдите все значения p, прикаждом из которых для любого
q система
х у 1
y q x p
2
2
имеет решения.
15.
Рассмотрим первое уравнение2
2
x+y =1
Заметим, что выражение
является уравнением
окружности с центром в точке
(0; 0) и радиусом равным
одному.
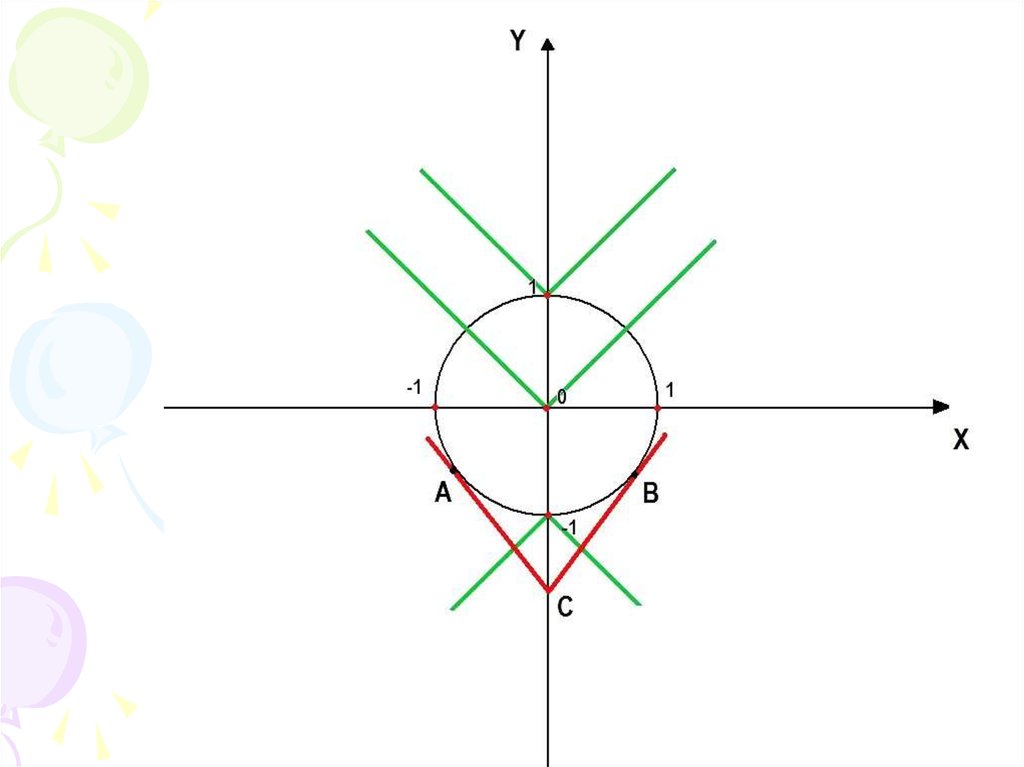
16.
Теперь исследуем второе выражение:y = q|x| + p
Графиком |х| является так называемая
галочка. От коэффициента q зависит
насколько отдалены от оси OY её
ветви и куда они направлены, так
при q<0 они будут направлены вниз,
а при q>0 верх.
От коэффициента р зависит
передвижение графика по оси OY.
Для наглядного решение нам
потребуется построение графика.
17.
18.
Таким образом система будет иметьрешение при p >= -1 и p <= 1.
Ответ: p принимает значения из
промежутка [-1;1].
19.
Найдите все положительные aпри каждом из которых система
уравнений
2
2
х 9 у 5 9
2
2
2
х
3
у
а
имеет единственное решение
20. Решение.
Для того чтобы решить задачу вамнеобходимо знать уравнение
окружности.
2
2
(x - х ) + (y - y ) = R
2
21.
Рассмотрим первое выражение:2
2
(|x|- 9) + (y-5) = 9
Из него следует, что центр
окружности будет находиться в
точке (9; 5), а также в точке (-9;
5), так как Х находится под знаком
модуль, а радиус этих двух
окружностей будет равен 3.
(Квадратный корень из 9 равен 3)
22.
Теперь рассмотрим второевыражение:
2
2
(x+3) + y = a2
Это выражение с параметром,
значение которого нам нужно
найти, а также уравнение
окружности с центром в точке
(-3; 0) и радиусом равным a.
Для наглядного решение нам
потребуется построение
окружностей.
23.
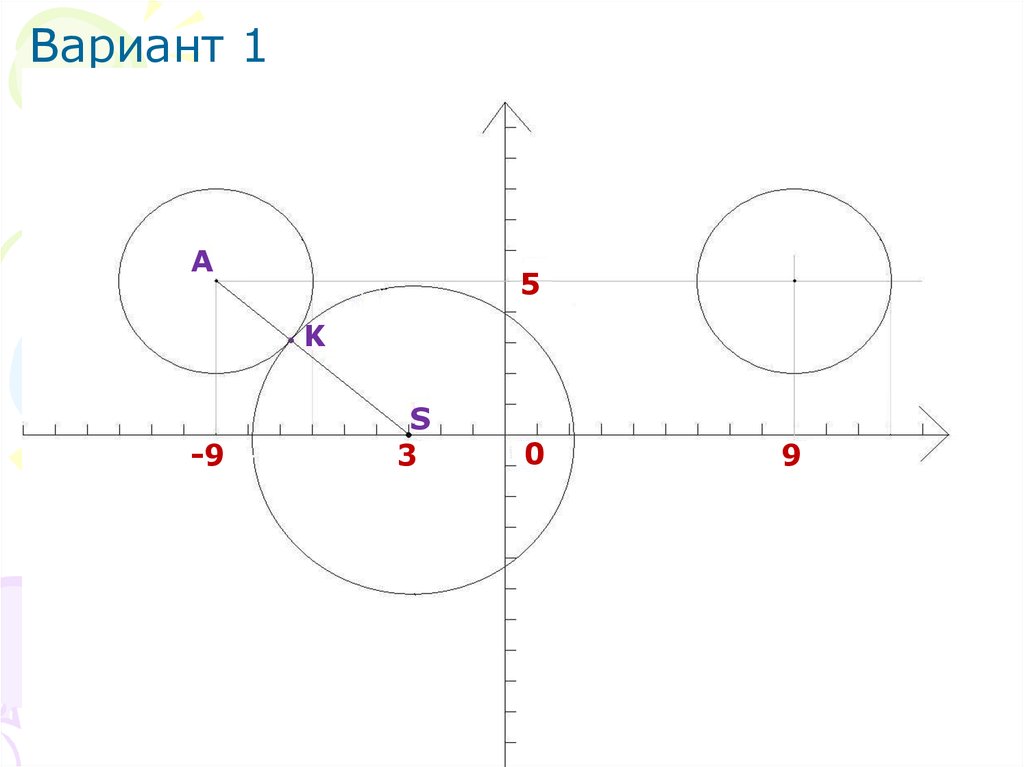
Вариант 1A
5
K
-9
S
3
0
9
24.
Расстояние KS = AS-AKAS можно найти по формуле
расстояния между двумя точками на
плоскости
AS=
AS= 61
AK=R=3 следовательно
KS =
61
-3
25.
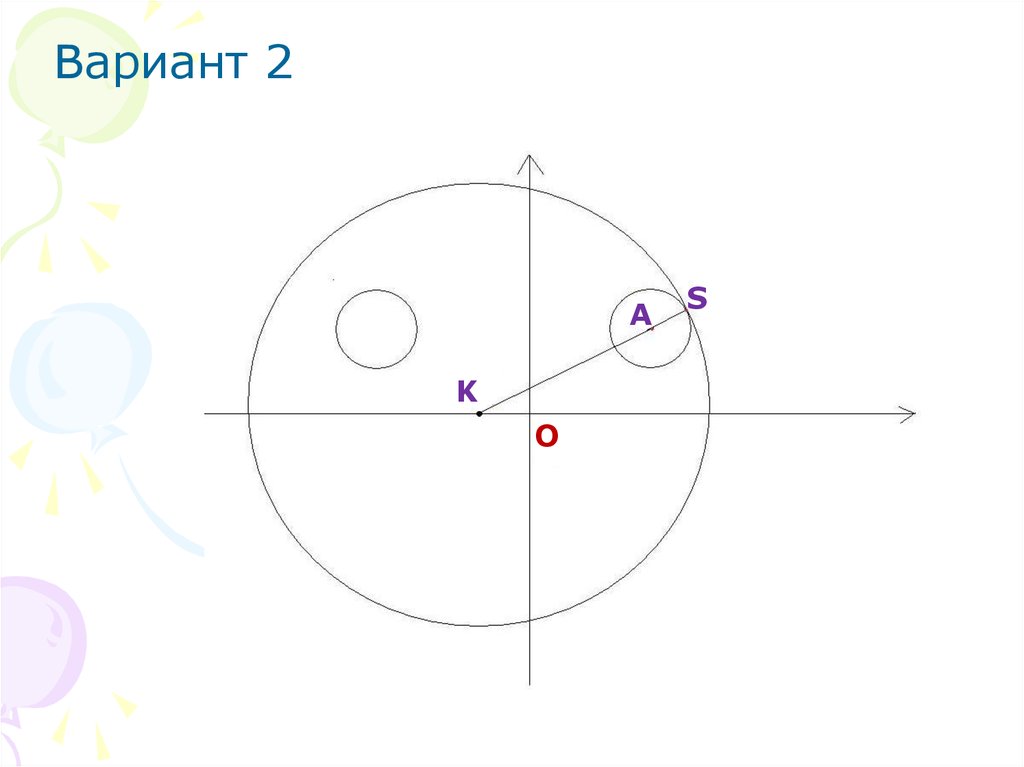
Вариант 2A
K
O
S
26.
Расстояние KS=AS+AKAK также можно найти по ранее
изложенной формуле
AK = 13
AS = R = 3
KS = 13 + 3 = 16
ОТВЕТ: Система имеет одно решение
при a=16 и когда а принимает
значение
61 - 3.
27. a=|x -4|x||?
Сколько корнейимеет уравнение
2
a=|x -4|x||?
28. 1) y=x -4x
2Построим
график
данной
функции:
х=2; у=-4
(вершина)
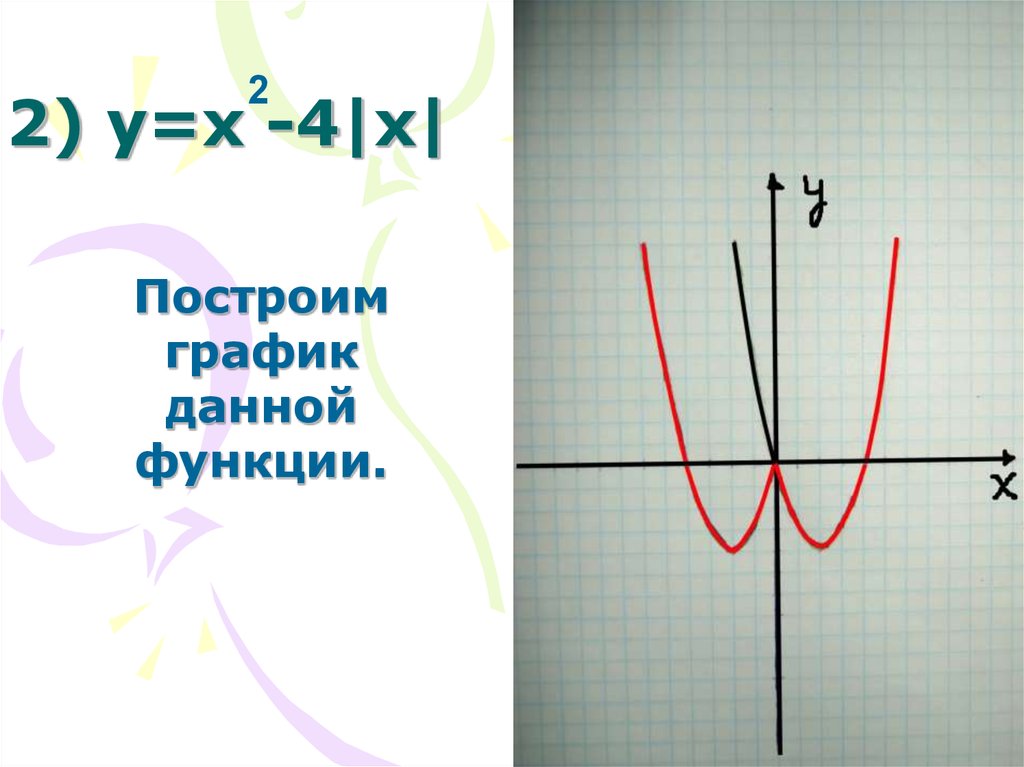
29. 2) у=x -4|x|
22) у=x -4|x|
Построим
график
данной
функции.
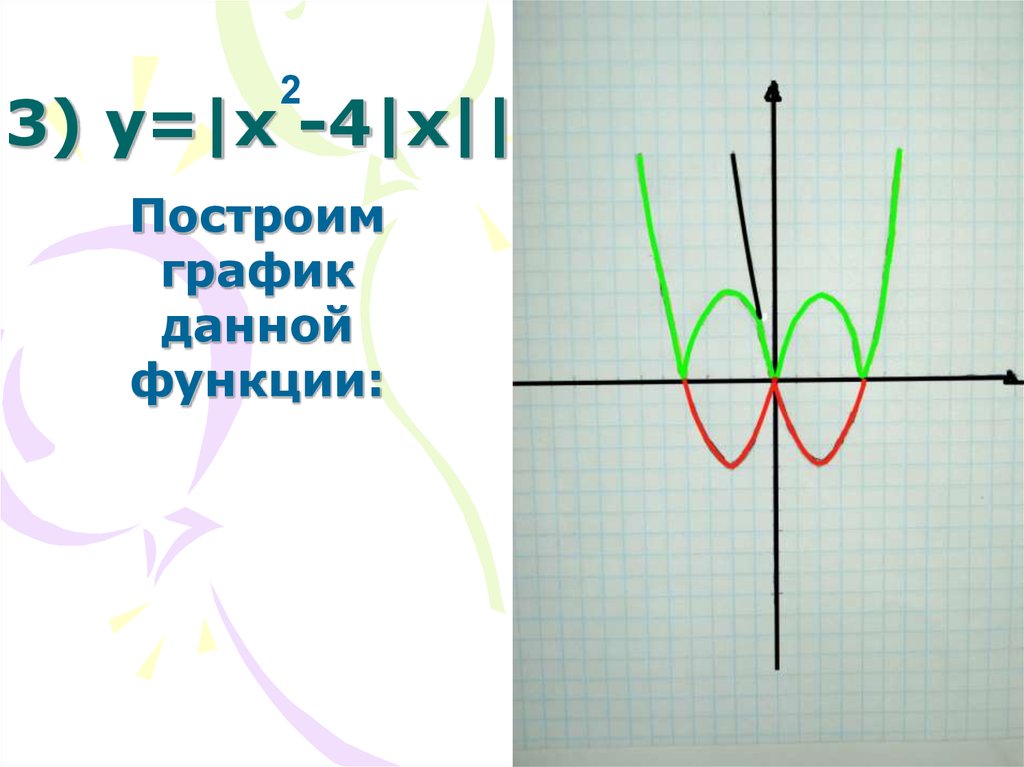
30. 3) у=|x -4|x||
23) у=|x -4|x||
Построим
график
данной
функции:
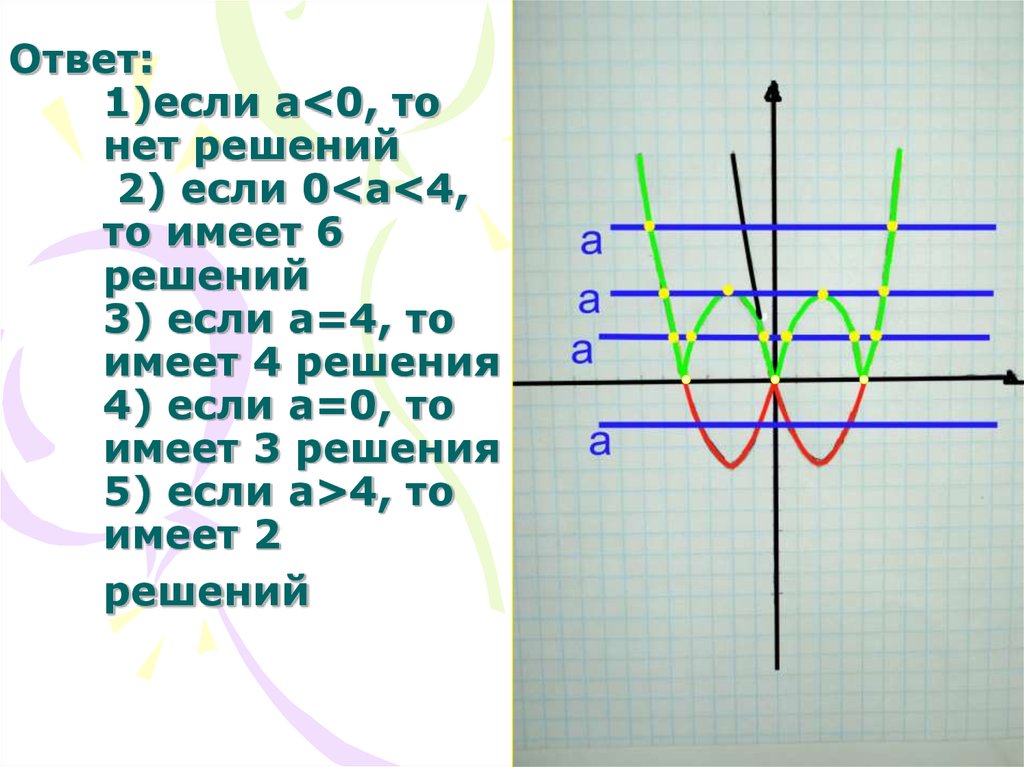
31. Ответ: 1)если a<0, то нет решений 2) если 0<a<4, то имеет 6 решений 3) если а=4, то имеет 4 решения 4) если а=0, то имеет 3
Ответ:1)если a<0, то
нет решений
2) если 0<a<4,
то имеет 6
решений
3) если а=4, то
имеет 4 решения
4) если а=0, то
имеет 3 решения
5) если а>4, то
имеет 2
решений
32.
Найти все значения параметра a,при каждом из которых система
уравнений
5 x 2 60 12 y ;
2
2
2
4 x 1 y a x .
имеет ровно 8 решений.
33.
x a y b2
2
c2
- уравнение окружности ;
(a ; b) – центр окружности; с – радиус.
x y 1
1.
- уравнение ромба .
4 x 1 y 2 a 2 x 2
( x 2) y a
2
2
2
2.
5 x 2 60 12 y
5 x 2 12 y 60
(-2 ; 0) - центр окружности; y = 0; x = 10; x = -14;
x = -2; y = ± 5;
a – радиус.
Решение системы – точки пересечения графиков.
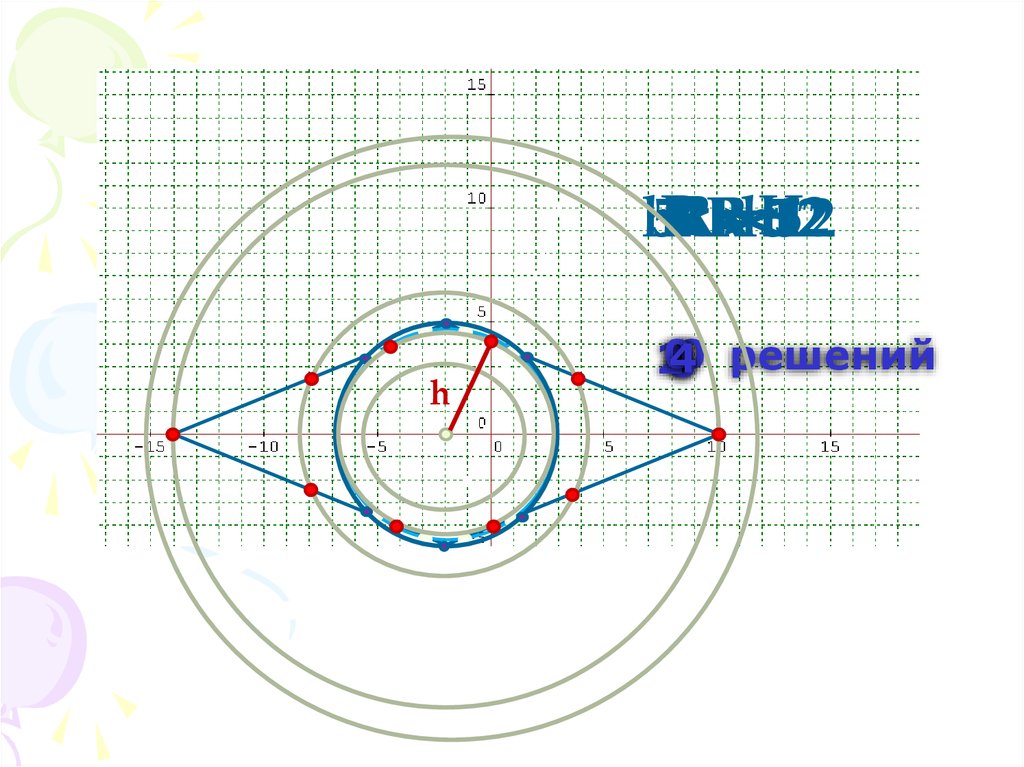
34.
R=>=H
h<R<5
5<R<12
R
R<h
512
h
0
4
2
6
80 решений
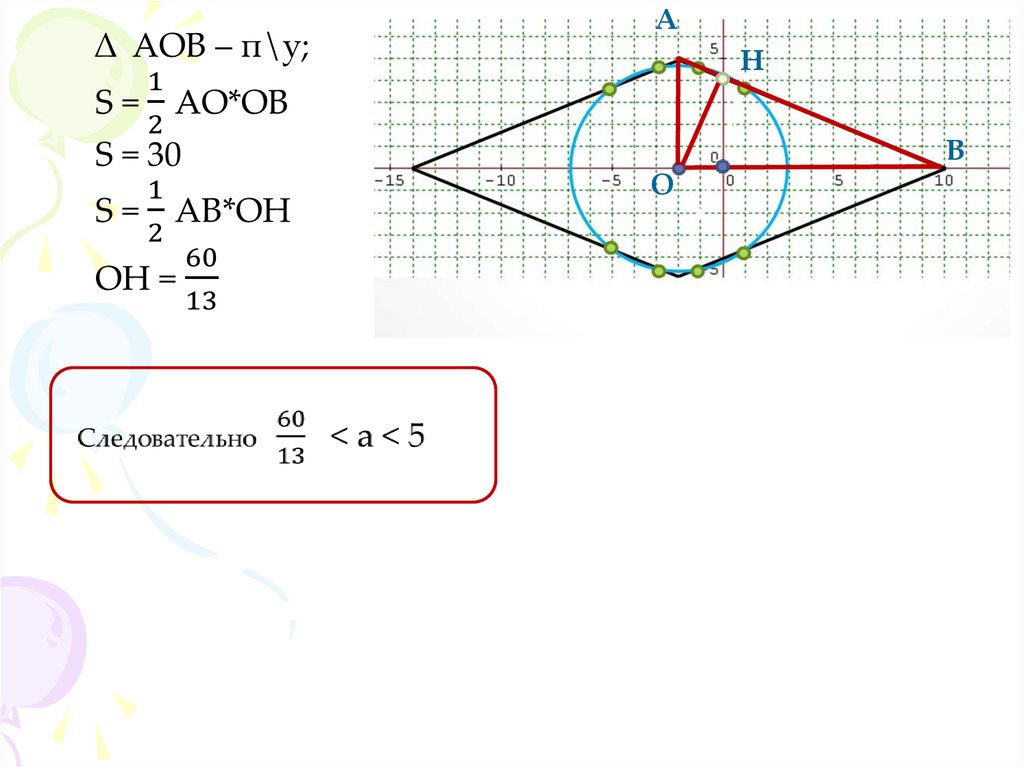
35.
АН
B
О
36.
f ( x) x 3 x a 5 x2
2
1.Найти а при котором данная
функция имеет более двух точек
экстремума
2.Найдите все значения параметра a
при каждом из которых функция
имеет хотя бы одну точку максимума
37. Раскрываем модуль: 1)
f ( x) x 3 x a 5 x2
2
Раскрываем модуль:
1) x 3x 3a 5 x x 8 x 3a
2
При х
2
a
2
2
2) x 3a 3x 5 x x 2 x 3a
2
При х
2
a
2
2
2
2
38. Найдем вершины парабол
b4
1) x0
2a
2) x0 1
Приравняем функции и найдем
значение а
x 8 x 3a x 2 x 3a
2
2
а =х
2
2
2
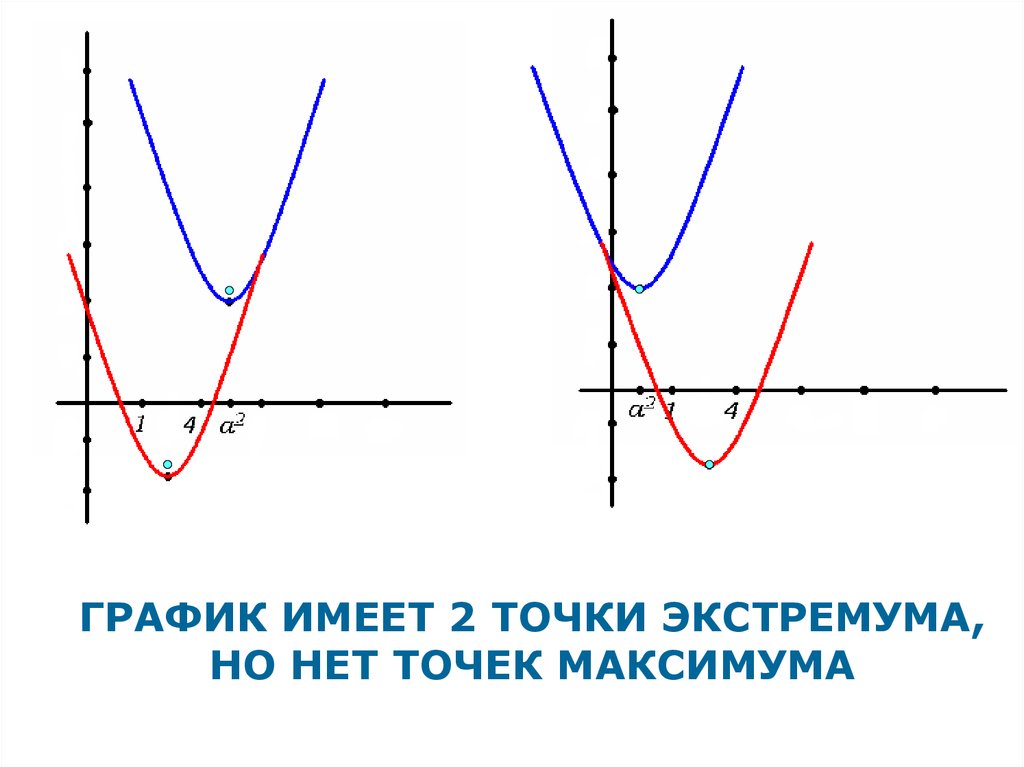
39.
ГРАФИК ИМЕЕТ 2 ТОЧКИ ЭКСТРЕМУМА,НО НЕТ ТОЧЕК МАКСИМУМА
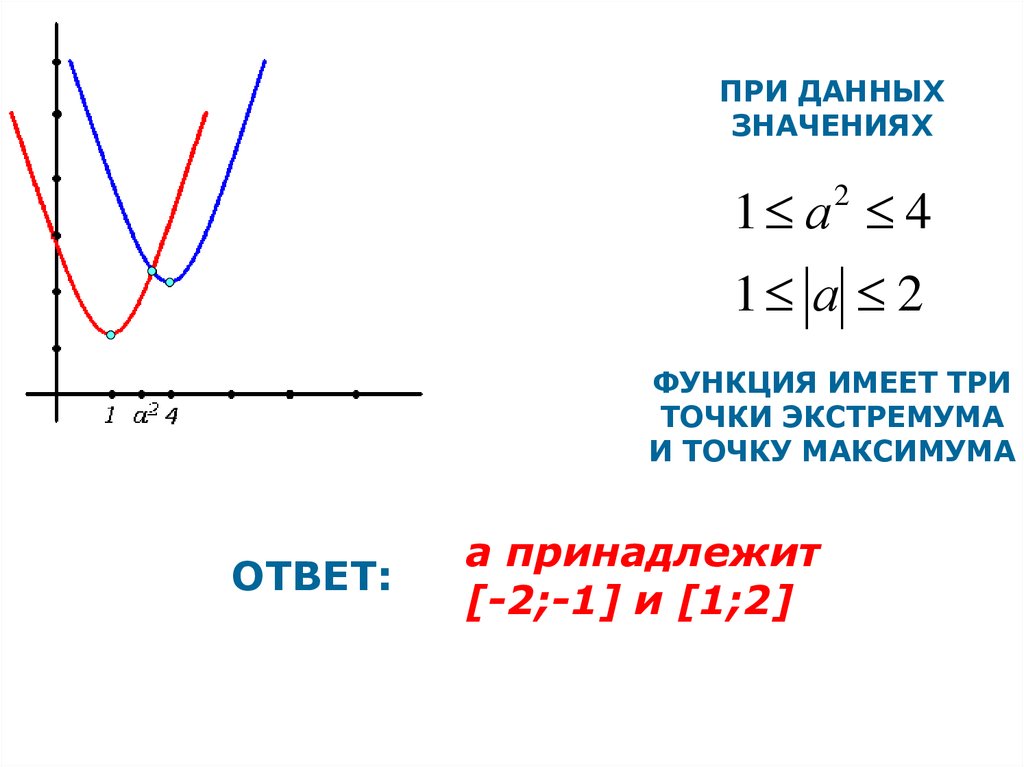
40.
ПРИ ДАННЫХЗНАЧЕНИЯХ
1 а 4
2
1 а 2
ФУНКЦИЯ ИМЕЕТ ТРИ
ТОЧКИ ЭКСТРЕМУМА
И ТОЧКУ МАКСИМУМА
ОТВЕТ:
а принадлежит
[-2;-1] и [1;2]
41. Благодорим ребят:
Радимушкина Дмитрия,Заботину Аллу,
Иванову Алину,
Клушенцову Александру,
Дорофееву Элеонору,
Сонину Маргариту,
Поводову Анастасию,
Янушевского Олега ,
ЗА ПОМОШЬ В ПОДГОТОВКЕ
ПРЕЗЕНТАЦИИ.








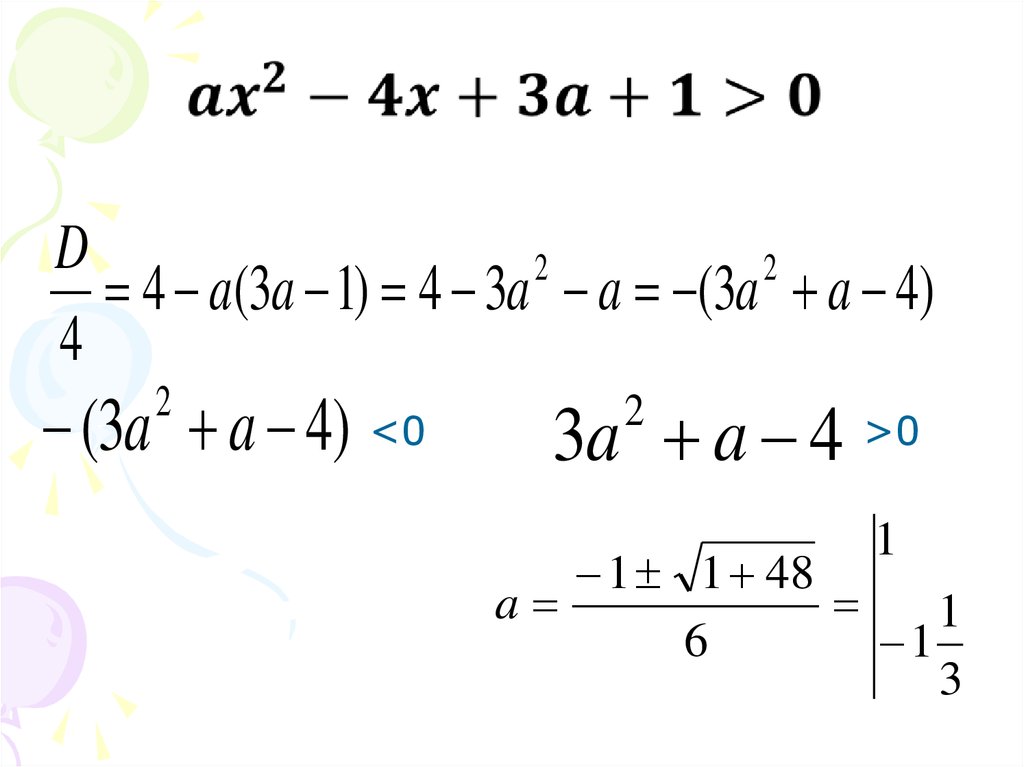











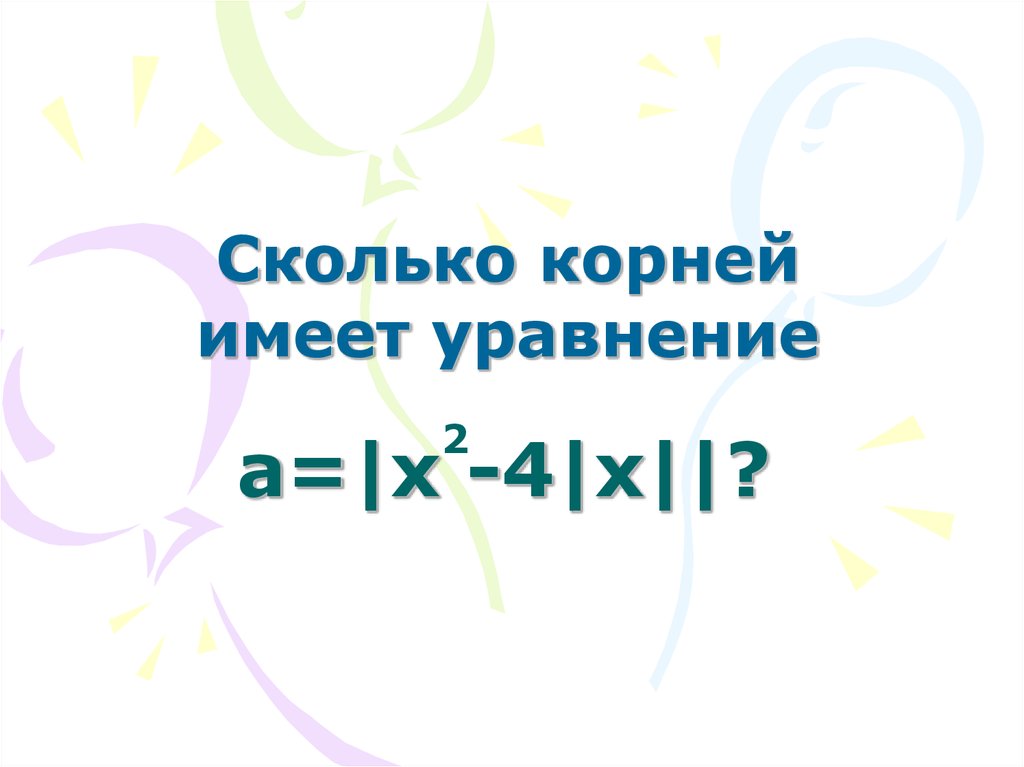
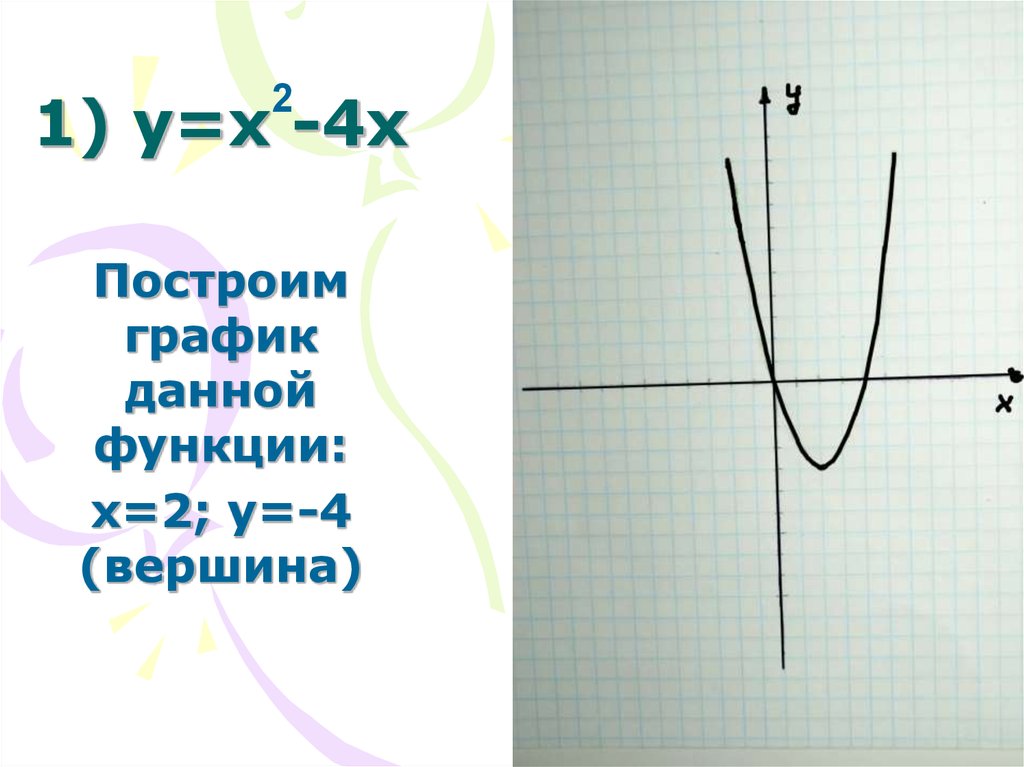






 mathematics
mathematics








