Уравнения повышенной сложности. Уравнения с параметрами

1. Уравнения повышенной сложности

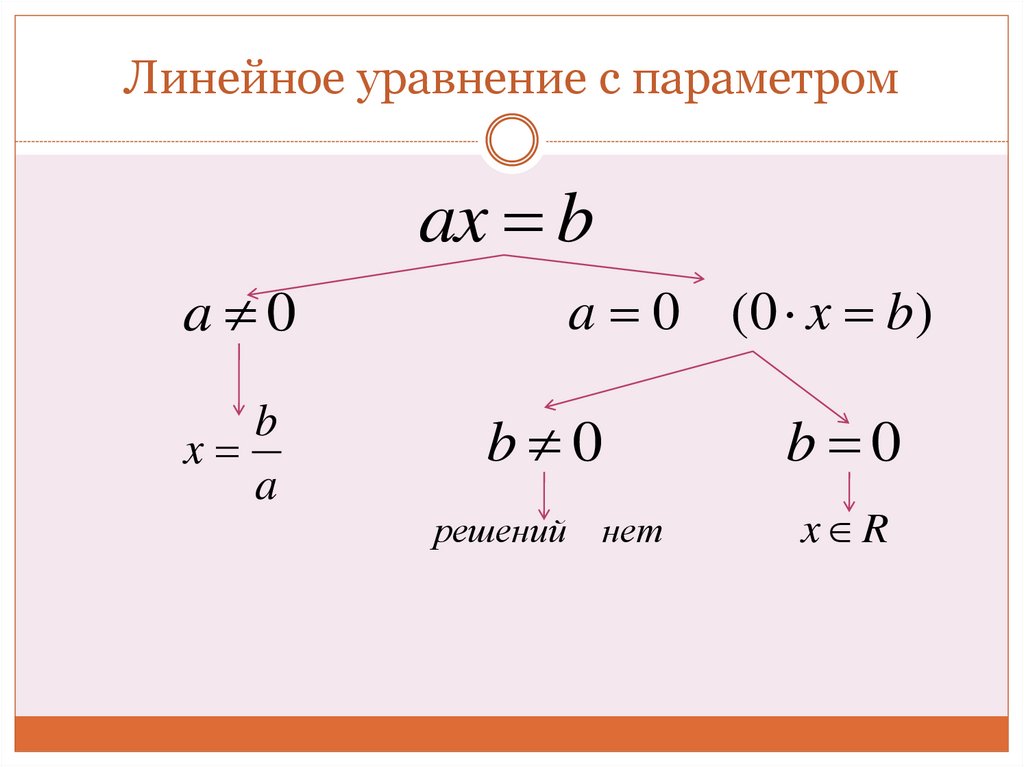
УРАВНЕНИЯ С ПАРАМЕТРАМИ

2. Уравнение с параметром

2x 5 2 x
2x 5 3 x
2 x 5 0,5 x
2x 5 a x

3. Уравнение с параметром. Основные понятия

Параметр - переменная величина, вместо
которой можно подставить числовое значение и
получить заданное уравнение.
Решить уравнение, содержащее
параметры, это значит, для каждой допустимой
системы значений этих параметров найти
множество всех решений заданного уравнения.

4. Типы заданий с параметрами

Тип 1. Уравнения, неравенства, их системы и совокупности, которые
необходимо решить либо для любого значения параметра
(параметров), либо для значений параметра, принадлежащих заранее
оговоренному множеству.
Тип 2. Уравнения, неравенства, их системы и совокупности, для
которых требуется определить количество решений в
зависимости от значения параметра (параметров).
Тип 3. Уравнения, неравенства, их системы и совокупности, для
которых требуется найти все те значения параметра, при
которых указанные уравнения, неравенства, их системы и
совокупности имеют заданное число решений (в частности, не
имеют или имеют бесконечное множество решений).
Тип 4. Уравнения, неравенства, их системы и совокупности, для
которых при искомых значениях параметра множество
решений удовлетворяет заданным условиям в области
определения.

5. Типы заданий

Для каждого значения параметра найти все
решения заданного уравнения (неравенства).
Найти все значения параметра, при каждом из
которых решения уравнения (неравенства)
удовлетворяют заданным требованиям.

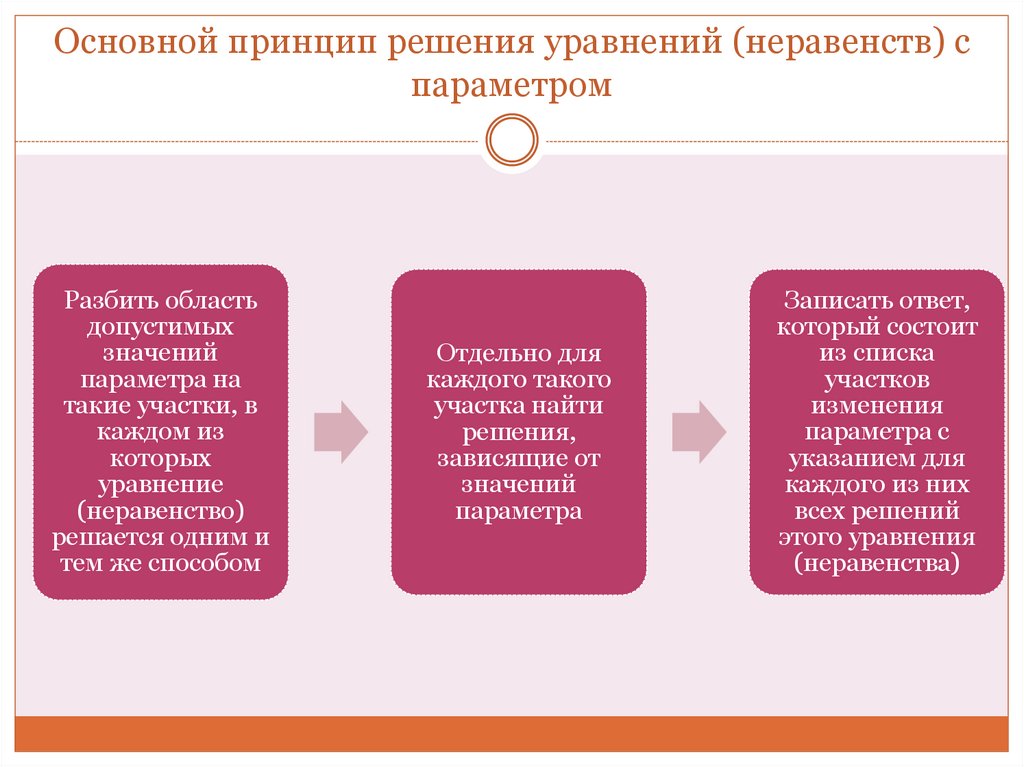
6. Основной принцип решения уравнений (неравенств) с параметром

Разбить область
допустимых
значений
параметра на
такие участки, в
каждом из
которых
уравнение
(неравенство)
решается одним и
тем же способом
Отдельно для
каждого такого
участка найти
решения,
зависящие от
значений
параметра
Записать ответ,
который состоит
из списка
участков
изменения
параметра с
указанием для
каждого из них
всех решений
этого уравнения
(неравенства)

7. Способы решения задач с параметрами

Способ I (аналитический). Это способ так называемого
прямого решения, повторяющего стандартные процедуры
нахождения ответа в задачах без параметра.
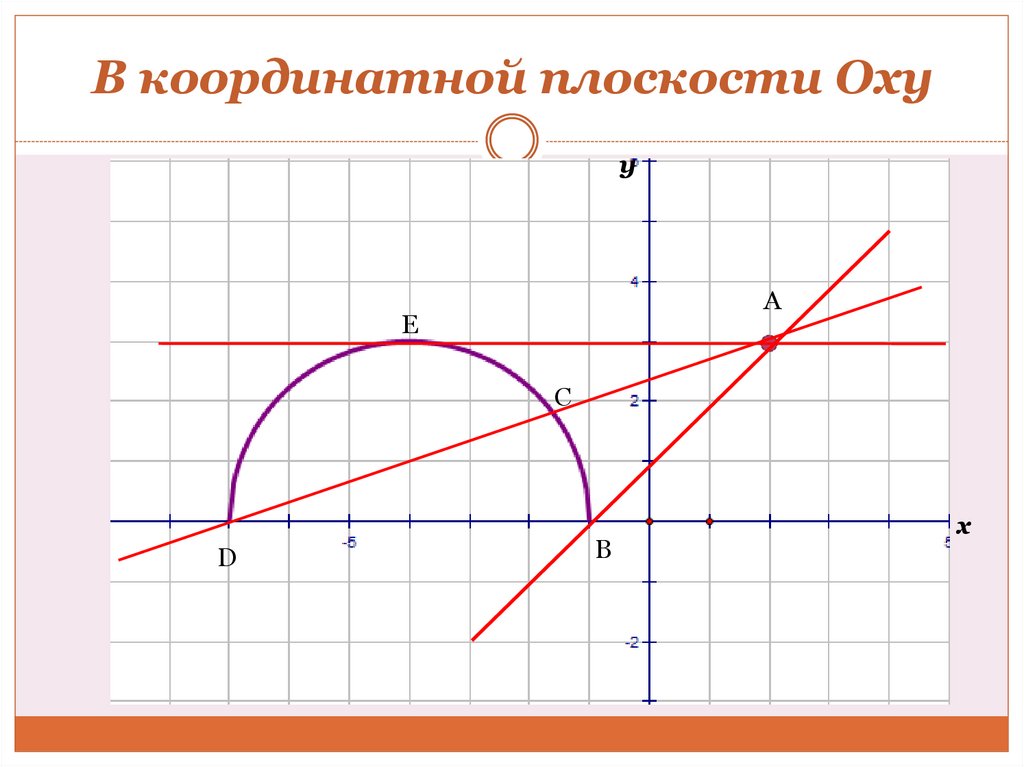
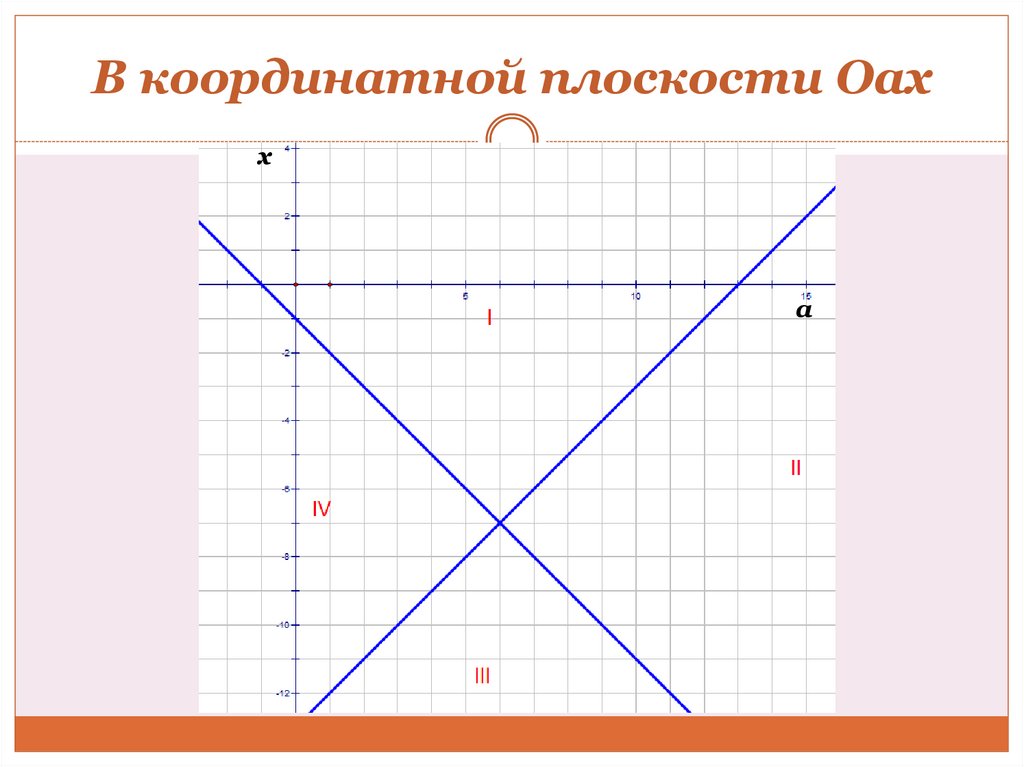
Способ II (графический). В зависимости от задачи (с
переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной
плоскости (x; a).
Способ III (решение относительно параметра). При
решении этим способом переменные x и a принимаются
равноправными и выбирается та переменная, относительно
которой аналитическое решение признается более простым.
После естественных упрощений возвращаемся к исходному
смыслу переменных x и a и заканчиваем решение.

8. Специфика уравнений (неравенств) с параметром состоит в том, что изменение значений параметра влечет за собой изменение не

только
коэффициентов,
но и ряда других
характеристик
Степень уравнения (Например,
уравнение