Целое уравнение с параметром

1. Целое уравнение с параметром

Методическая разработка к учебнику Ю.Макарычева
«Алгебра-9» углубленное изучение
Драгунова Е.Ю. учитель математики МОУ СОШ № 10 г.о.Жуковский

2. Что такое уравнение с параметром?

22.01.2017
Что такое уравнение с параметром?
• Решить уравнение:
6х-1 = х+6
6х-х = 6+1
5х = 7
х = 7:5
ах
х = 1,4
56х-1
= х+65
4х -1 = х + 4
3х – 1 = х + 3
-1=х+а
Это – уравнение
с параметром

3. Определения

22.01.2017
• Уравнение с переменной х в котором один или
несколько коэффициентов обозначены буквой,
называется уравнением с параметром.
• Параметр – это фиксированное число, значение
которого в каждом конкретном случае известно.
1
3х 7, 5 х 7, х 7, 0 х 7
3
ах = 7
х- переменная
а- параметр

4. Определения

22.01.2017
• Решить уравнение с параметром - это значит
установить соответствие, позволяющее для
любого значения параметра решить уравнение,
т.е. найти множество его корней.
Задания
в зависимости от параметра
Найти
количество корней
Решить уравнение
при каждом а

5. Вернемся к уравнению

22.01.2017
ах - 1 = х + а – линейное уравнение
ах – х = а + 1
х(а – 1) = а + 1
Не будем торопиться с делением на (а -1), т.к.
при а = 1 выражение обращается в нуль.
Рассмотрим возможные случаи:
1) Если а = 1, то уравнение имеет вид 0 х = 2 и
значит в этом случае данное уравнение не
имеет корней.
2) Если а = 1, то на (а – 1) = 0 можно делить
а 1
х
единственный корень
а 1

6.

22.01.2017
• На числовой прямой покажем, что мы не
пропустили ни одного значения параметра а, не
указав при этом значения х, которое соответствует
данному значению а
а 1
х
а 1
Ǿ
а 1
х
а 1
1
Ответ: при а = 1 корней нет;
а 1
при а =1 -
х
а 1
а

7. Пример 2 решить уравнение (а-2)(а+5)х = (а+1)(а – 2)

Пример 2
22.01.2017
решить уравнение
(а-2)(а+5)х = (а+1)(а – 2)
• Рассмотрим возможные случаи:
• 1) Если а = 2, то уравнение имеет вид 0х =0 и его
решением является любое действительное число;
• 2) Если а = -5, то уравнение имеет вид 0х = 28 и не имеет
корней;
• 3)Если а =2 и а = -5, то уравнение имеет единственный
корень
(а 1)( а 2) а 1
х
(а 2)( а 5) а 5
Ответ : приа 2 х R, при а 5 корней нет
а 1
при а ( ; 5) ( 5;2) (2; ) х
а 5

8. Квадратные уравнения с параметром

22.01.2017
Квадратные уравнения с параметром
Решить уравнение: (а+4)х2+2х(а+6)+2а+9=0
При любом ли значении а данное уравнение является квадратным?
1. Если (а+4)=0, то уравнение не будет квадратным
Если а = - 4, то уравнение имеет вид: 4х+1= 0 и х = -1/4
2. Если а = - 4, то уравнение квадратное, значит находим дискриминант
D (a 6) 2 (a 4)(2a 9) a(а 5)
-
-
+
-5
При а ( ; 5) (0; )
-4
а
0
D 0 корней нет
При а 0 или а 5 D 0 корень один
При аПри
( а5
; (4 )5 ;0() 4D
;0) 0D
0
корней
корней
два два

9.

D a(а 5)
22.01.2017
+
-5
-4
При а ( ; 5) (0; )
-
а
0
D 0 корней нет
При а ( 5; 4) ( 4;0) D 0 корней два
При а 0
или
(а 6) а(а 5)
х
а 4
а 5
х1 х2 1,5
D 0 корень один (ддвано совпавших)
х1 х2 1
1
Ответ : при а 4 х ;
4
при а ( ; 5) (0; ) корней нет
- (а 6) - а(а 5)
при а [ 5; 4) ( 4;0] х
а 4

10. Расположение нулей квадратичной функции на координатной прямой

22.01.2017
Расположение нулей квадратичной
функции на координатной прямой
• Пусть дана функция у = ах2+bх + с, а 0
• х1 и х2 нули этой функции (корни уравнения
ах2+bх + с=0) и х2 х1
• Числа α и β
Условия, которые придется учитывать:
1. Знак дискриминанта (корни должны быть)
2. Формула для нахождения координат вершины параболы
3. Направление ветвей параболы
4. Знак числа f(α) и f(β)

11.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
1)Оба корня меньше α
х1
х2
α
х
D 0
xв
a f ( ) 0

12.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
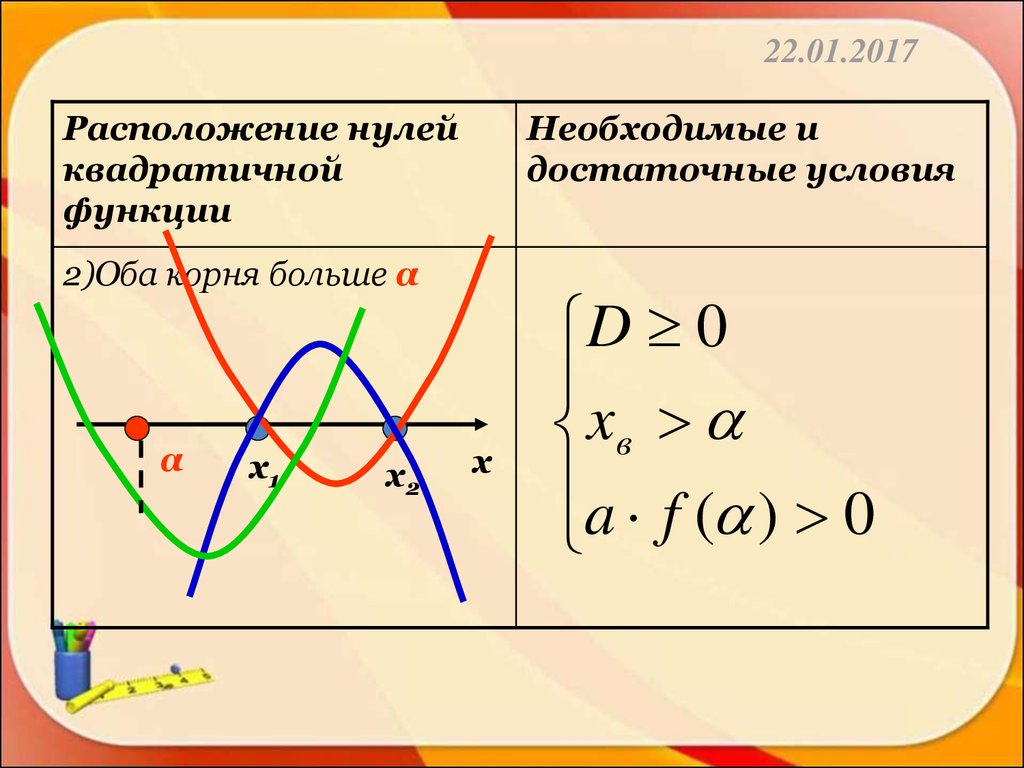
2)Оба корня больше α
α
х1
х2
х
D 0
xв
a f ( ) 0

13.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
3) α лежит между
корнями
х1
α
х2
х
D 0
a f ( ) 0

14.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
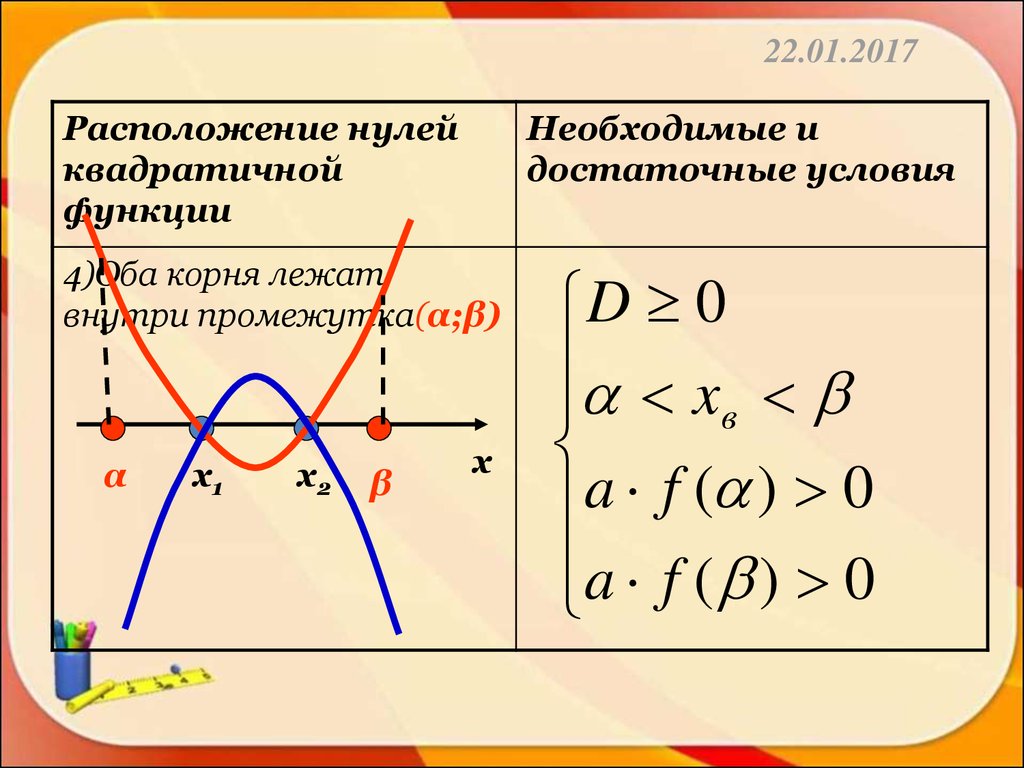
4)Оба корня лежат
внутри промежутка(α;β)
α
х1
х2
β
х
D 0
x
в
a f ( ) 0
a f ( ) 0

15.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
5)Меньший корень лежит
внутри промежутка(α;β)
α
х1
β
х2
х
D 0
a f ( ) 0
a f ( ) 0

16.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
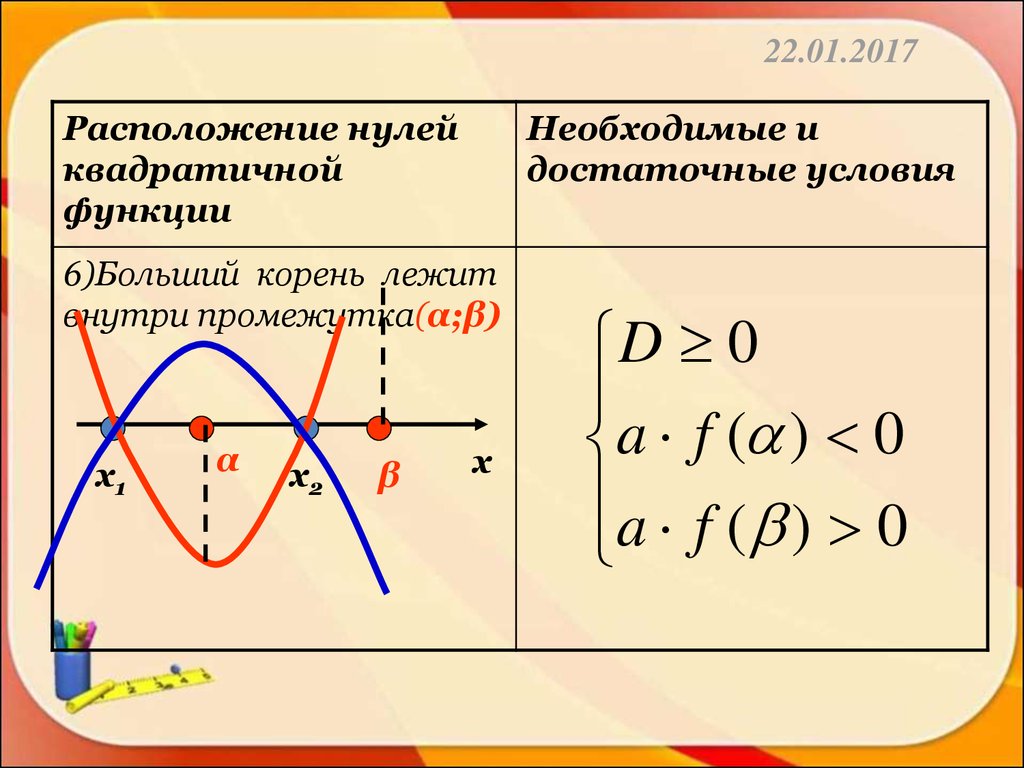
6)Больший корень лежит
внутри промежутка(α;β)
х1
α
х2
β
х
D 0
a f ( ) 0
a f ( ) 0

17.

22.01.2017
Расположение нулей
квадратичной
функции
Необходимые и
достаточные условия
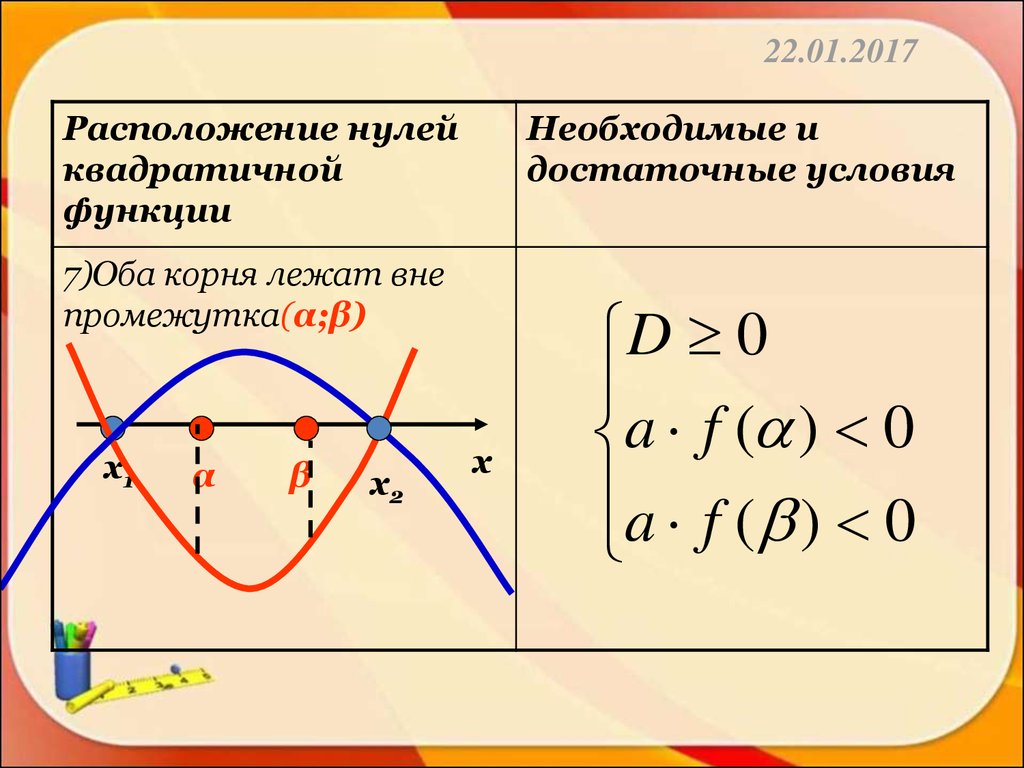
7)Оба корня лежат вне
промежутка(α;β)
х1
α
β
х2
х
D 0
a f ( ) 0
a f ( ) 0

18.

22.01.2017
х 2 ах 2
2,
2
х х 1
2
х ах 2 3.
х2 х 1
1. Найти все значения параметра а,
при которых решением системы
является вся прямая.
2. При каких значениях
параметра р функция
определена при всех хєR ?
5
у (4 р) х 5х (1 р)
8
3. При каких значениях параметра а
система неравенств
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечно много
решений?
2
х 2 8 х 15 0,
2
х (а 4) х 4а 0.

19.

1. Найти все значения параметра а,
при которых решением системы
является вся прямая.
Решение.
х 2 ах 2
2,
2
х х 1
2
х ах 2 3
х 2 х 1
х 2 ах 2
2,
2
х х 1
2
х ах 2 3.
х 2 х 1
х 2 ах 2 2 х 2 2 х 2
0,
2
х х 1
2
2
х
ах
2
3
х
3х 3
0
2
х х 1
22.01.2017
х 2 ( а 2) х 4
0,
2
х х 1
2
4 х (а 3) х 1 0.
х2 х 1
Так как квадратный трехчлен х2-х+1=(х2-2·0,5·х+0,25)+0,75= (х-0,5)2+0,75>0
Оцените
знаменатель
дробей.
при любом
значении
х, то получим систему
неравенств:
х 2 (а 2) х 4 0,
2
4 х (а 3) х 1 0.

20.

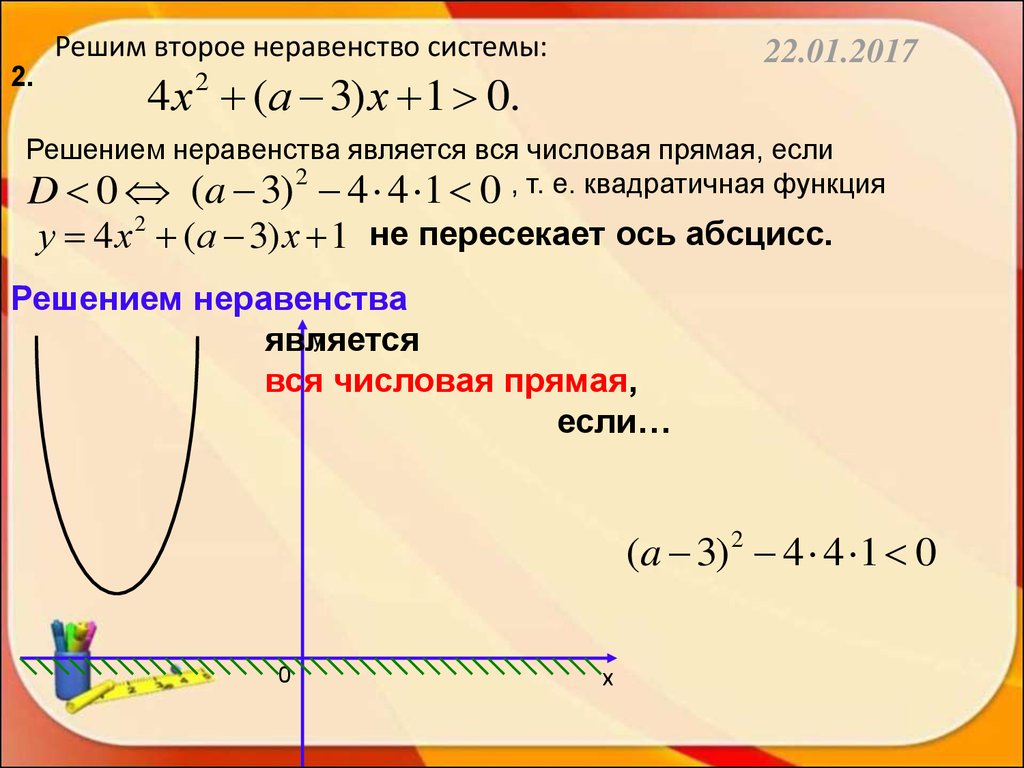
Решим второе неравенство системы:
2.
22.01.2017
4 х (а 3) х 1 0.
2
Решением неравенства является вся числовая прямая, если
D 0 (a 3) 2 4 4 1 0 , т. е. квадратичная функция
у 4 х 2 (а 3) х 1 не пересекает ось абсцисс.
Решением неравенства
у
является
вся числовая прямая,
если…
(a 3) 2 4 4 1 0
0
х

21. Решим систему неравенств:

(а 2) 2 16 0,
(а 3) 2 16 0
(а 6)( а 2) 0,
(а 1)( а 7) 0
+
-
а 2 4а 12 0,
2
а 6а 7 0
6 а 2,
1 а 7.
а
2
-
+
+
-6
22.01.2017
-1
Ответ: (-1;2).
-6
-1
2
7
а
+
7
а

22. 2. При каких значениях параметра р функция определена при всех хєR ?

22.01.2017
5
у (4 р) х 5х (1 р)
8
2
Решение.
Область определения функции - множество
действительных
чисел, удовлетворяющих условию…
5
(4 р ) х 2 5 х (1 р) 0
8
Какие условия должны выполняться, чтобы решением этого
неравенства (4 р ) х 2 5 х 5 (1 р ) 0 являлась вся числовая
8
прямая?
D 0,
4 р 0
5
25
4
(1 р)( 4 р ) 0,
8
р 4
р 1,
6,
р
р 4
р 1.
р 2 5 р 6 0,
р 4
Ответ:(-∞ ; -1].