Квадратные уравнения

1.

КОМПЬЮТЕРНАЯ ПРЕЗЕНТАЦИЯ
МЕТОДИЧЕСКОЙ РАЗРАБОТКИ РАЗДЕЛА
ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ
Выполнила
учитель математики
МБОУ СОШ №59
Спирина Т.В.
21.10.2013 г.

2. Тема: Квадратные уравнения

Цели:
Тема: Квадратные
уравнения
Образовательные
Выработать прочные навыки решения различных видов квадратных
уравнений, используя формулы для решения квадратных уравнений
или теоремы Виета и уравнений, сводящихся к квадратным, и
применять их к решению задач.
Воспитательные
Способствовать выработки у учащихся желания и потребности
обобщения изучаемых фактов: развивать самостоятельность и
творчество. Воспитывать аккуратность, доброжелательность,
взаимопомощь.Учить самоконтролю, взаимоконтролю.
Развивающие
Развивать внимание, логическое мышление, приемы сравнения,
умение анализировать полученный результат и делать выводы.
Развивать математическую речь, память.

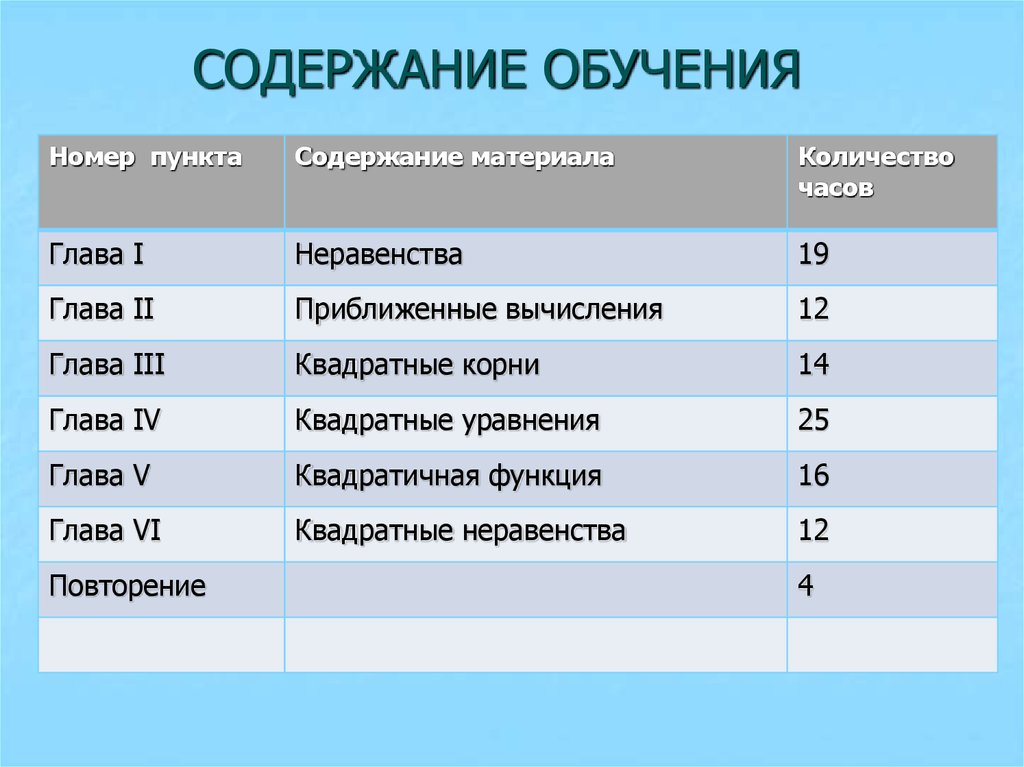
3. СОДЕРЖАНИЕ ОБУЧЕНИЯ

Номер пункта
Содержание материала
Количество
часов
Глава I
Неравенства
19
Глава II
Приближенные вычисления
12
Глава III
Квадратные корни
14
Глава IV
Квадратные уравнения
25
Глава V
Квадратичная функция
16
Глава VI
Квадратные неравенства
12
Повторение
4

4.

Биквадратные
уравнения
Дробнорациональные
уравнения
Квадратичная
функция
Квадратные
неравенства
Квадратные уравнения
Иррациональные
уравнения и
неравенства
Показательные
уравнения и
неравенства
Арифметическая
и геометрическая
прогрессии
Логарифмичес
кие уравнения
и неравенства
Производная
(исследование
функции)
Тригонометриче
ские уравнения
и неравенства
Интеграл
(нахождение
площадей фигур)

5.

Способы решения
квадратных уравнений
Метод
выделения
полного
квадрата
Формула
корней
квадратного
уравнения
Разложение левой
части уравнения на
множители
Формула
четного второго
коэффициента
Способ «переброски»
коэффициента
По теореме
Виета
По свойству
коэффициентов

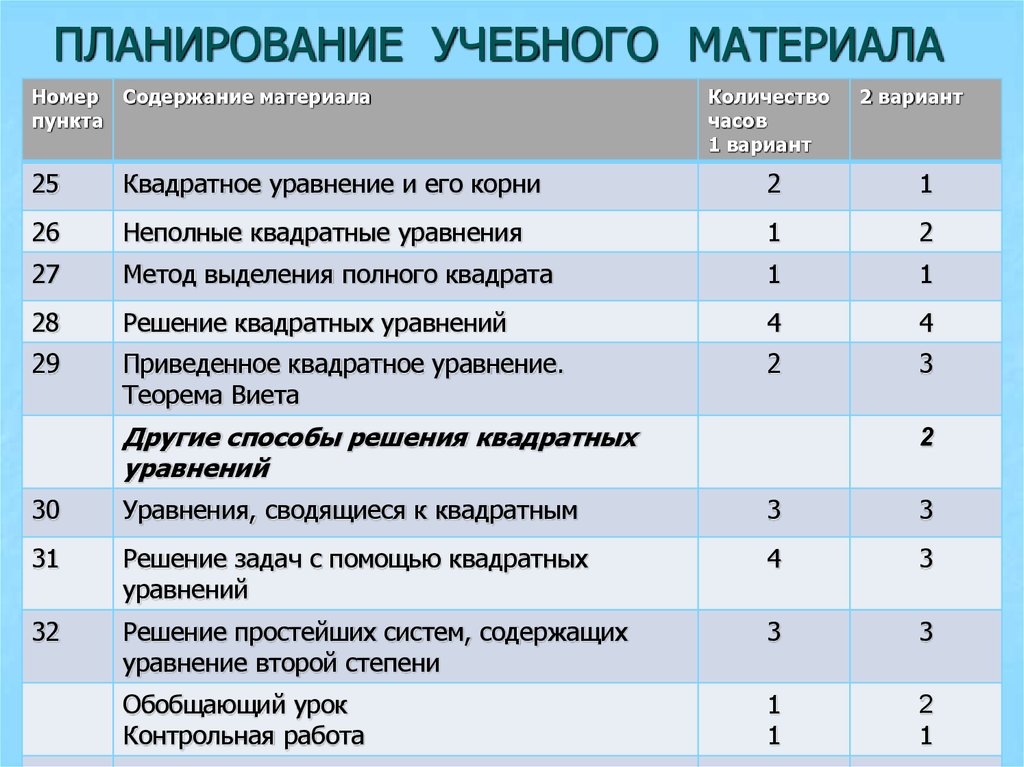
6. ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА

Номер Содержание материала
пункта
Количество
часов
1 вариант
2 вариант
25
Квадратное уравнение и его корни
2
1
26
Неполные квадратные уравнения
1
2
27
Метод выделения полного квадрата
1
1
28
Решение квадратных уравнений
4
4
29
Приведенное квадратное уравнение.
Теорема Виета
2
3
Другие способы решения квадратных
уравнений
2
30
Уравнения, сводящиеся к квадратным
3
3
31
Решение задач с помощью квадратных
уравнений
4
3
32
Решение простейших систем, содержащих
уравнение второй степени
3
3
Обобщающий урок
Контрольная работа
1
1
2
1

7. КВАДРАТНЫЕ УРАВНЕНИЯ

Решите задачу:
Прямоугольный газон обнесён
изгородью, длина которой 30 см.
Площадь газона 56 кв. см. Найдите
стороны газона.
15 - х
КВАДРАТНЫЕ УРАВНЕНИЯ
ПОЛНЫЕ
НЕПОЛНЫЕ
х
КВАДРАТНЫЕ УРАВНЕНИЯ
Х( 15 - х ) = 56
х 2 15 х 56 0
ПРИВЕДЕННЫЕ
НЕПРИВЕДЕННЫЕ

8. КВАДРАТНЫЕ УРАВНЕНИЯ

Запишите квадратное уравнение, у которого
первый коэффициент 3, второй коэффициент -5,
свободный член 2.
Запишите квадратное уравнение, у которого
первый коэффициент -7, второй коэффициент 2,
свободный член 0.
Запишите приведенное квадратное уравнение , у
которого второй коэффициент и свободный член
равны -2.
Запишите неполное квадратное уравнение, у
которого первый коэффициент равен -5, свободный
член равен 7.
Запишите приведенное неполное квадратное
уравнение , у которого второй коэффициент равен
9.
Запишите квадратное уравнение, если известны
его коэффициенты: а=2, в=3, с=-8.
Запишите квадратное уравнение, если известны его
коэффициенты: а=-1, в=0, с=9.
3х 5 х 2 0
2
7х 2х 0
2
х 2х 2 0
2
5х 7 0
2
х 9х 0
2
2 х 3х 8 0
2
х 9 0
2

9. Неполные квадратные уравнения

в о, с 0
ах 2 с 0
х2
ах вх 0
2
с
а
а и с имеют
разные знаки
а и с имеют
одинаковые
знаки
2 корня
Нет корней
х1, 2
с
а
в 0, с 0
х(ах в) 0
или
х 0
ах в 0
2корня
в
х 0илих
а
в 0, с 0
ах 2 0, а 0
х 0
2
1корень
х1, 2 0

10.

Алгоритм решения неполных квадратных
уравнений
Первый вид: ax2+bx=0 (при b≠0)
1.
2.
3.
Разложить на множители левую часть
уравнения
Произведение равно нулю тогда и только тогда,
когда один из множителей равен нулю
Решаем уравнения вида: ax+b=0 при a≠0
x(ax+b)=0
x=0 или ax+b=0
ax=-b
x
b
a
Второй вид: ax2+c=0 (при c≠0)
1.
Перенести свободный член уравнения в правую
часть и разделить обе части уравнения на a
x2
c
a
c
a
Так как c≠0, то 0
2.
если c 0 , то уравнение имеет два корня
a
если c 0
a
x1
c
и
a
, то уравнение не имеет корней.
Третий вид: ax2=0 (при a≠0)
Разделить обе части уравнения на a, получим
x2=0. Уравнение имеет единственный корень.
x=0
x1
c
a

11. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

ах вх с 0, а 0
2
D в 4ас
2
D 0
2 корня
D 0
1 корень
D 0
Нет корней
Формула корней:
х1, 2
х1, 2
в D
2а
в
D
2
4
2а

12.

Алгоритм решения полных квадратных уравнений
ax2+bx+c=0
1.
2.
Выполнить тождественные преобразования.
Выписать коэффициенты.
3.
Вычислить дискриминант и сравнить его с
нулём
4.
Если D>0, то уравнение имеет два корня
5.
Если D =0, то уравнение имеет один корень
6.
Если D <0, то корней нет.
D=b2- 4ac
b D
2a
b
x
2a
x1, 2

13. Задания для подготовки к ГИА

14. Задания для подготовки к ЕГЭ

15. ТЕОРЕМА ВИЕТА

х1
и
х2
корни уравнения
ах 2 вх с 0, а 0
х 2 рх q 0
в
х1 х2
а
с
х1 х2
а
х1 х2 р
х1 х2 q
ОБРАТНАЯ ТЕОРЕМА
Для чисел
х1 , х2
х1
, х2 , p, q
имеем:
корни уравнения
х1 х2 р
х1 х2 q
х 2 рх q 0

16.

17. СВОЙСТВО КОЭФФИЦИЕНТОВ

а+в+с=0
х1 1
с
х2
а
а-в+с=0
х1 1
самостоятельная работа
с
х2
а

18.

19.

20.

Контрольная работа
Решить уравнения:
9х 4
2
8х 7 х 0
2
3х 2 4 х 5 0
Решите задачу:
Периметр прямоугольника равен
32см. Найдите его стороны, если
известно , что площадь
прямоугольника равна 60 кв. см.
12 х 2 15 х 27 0
х 19 х 48 0
4
2
10 у
у 5
у 3
2
9 у 4 3 у 2 2 3 у.
Сократите дробь:
х 2 8х 7
х2 1
В уравнении
х 2 рх 18 0
один из его корней равен -9.
Найдите другой корень и
коэффициент р