Применение свойств квадратичной функции при решении уравнений с параметром

1. Презентация урока по алгебре в 9 классе.

Носкова Н.М., учитель математики
ГБОУ лицея № 344 Невского района
Санкт - Петербурга
1

2. Тема: Применение свойств квадратичной функции при решении уравнений с параметром.

Цель урока:
обобщить и систематизировать изученные
свойства квадратичной функции;
научить учащихся самостоятельно
формулировать теоремы о корнях квадратного
уравнения;
научить применять полученные теоремы для
решения задач с параметром;
развивать мыслительную деятельность, умение
анализировать, обобщать, делать выводы.
2

3.

Функция у = ax2 + bx + c, a ≠ 0 называется
квадратичной.
График квадратичной функции – парабола.
Если старший коэффициент квадратного
трехчлена больше нуля, то ветви параболы
направлены вверх.
Если старший коэффициент квадратного
трехчлена меньше нуля, то ветви параболы
направлены вниз.
3

4.

Если дискриминант больше нуля, то парабола
пересекает ось абсцисс в двух точках.
Если дискриминант равен нулю, то парабола
касается оси абсцисс.
Если дискриминант меньше нуля, то парабола
не имеет общих точек с осью абсцисс.
Абсцисса вершины параболы равна
b
x0
2a
.
Парабола пересекает ось ординат в точке ( 0; с).
4

5.

1. На рисунке изображён график квадратичной
функции у = ax2 + bx + c, a ≠ 0. Какое из
соотношений справедливо:
у
х
а) аb > 0;
б) са > 0; в) аb < 0; г) bс < 0 ?
5

6.

2. При каких значениях а парабола у = ах2 – 2х + 25
касается оси ОХ?
а) а = 25, б) а = 0 и а = 0,04; в) а = 0,04.
3. При каких значениях k уравнение kх2 – ( k – 7)х + 9 = 0
имеет два равных положительных корня?
а) k = 49, k = 1; б) k = 1;
в) k = 49.
4. При каких значениях а уравнение ах2 – 6х + а = 0 имеет
два различных корня?
а) (− 3; 0)U(0; 3);
б) (−3; 3);
в) (−∞; −3)U(3; +∞).
6

7. Правило 1.

Корни квадратного уравнения ax 2 bx c 0, a 0 больше
заданного числа M, если имеет место сиcтема:
у
f(M)
х0
М х1
х2
х
a 0,
D 0,
x0 M ,
f ( M ) 0,
у
М
х1
х0
f(M)
х2
х
a 0,
D 0,
x0 M ,
f ( M ) 0;
a f ( M ) 0,
D 0,
x M .
0
7

8. Правило 1.

a 0,
D
0
,
x0 M ,
a
f
(
M
)
0
,
f ( M ) 0,
M x1 x2
D 0,
a 0,
x M .
0
D 0,
x0 M ,
f ( M ) 0;
8

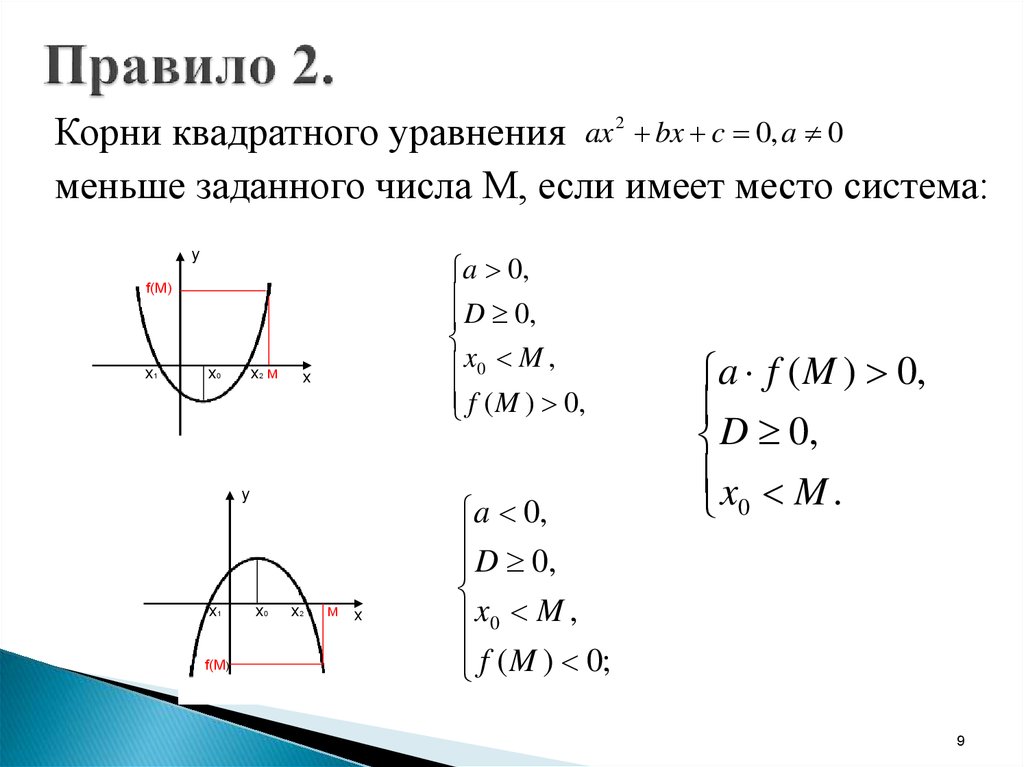
9. Правило 2.

Корни квадратного уравнения ax 2 bx c 0, a 0
меньше заданного числа М, если имеет место сиcтема:
у
a 0,
D 0,
x0 M ,
f ( M ) 0,
f(M)
х1
х0
х2 м
х
у
х1
f(M)
х0
х2
м х
a 0,
D 0,
x0 M ,
f ( M ) 0;
a f ( M ) 0,
D 0,
x M .
0
9

10. Правило 2.

a 0,
D
0
,
x0 M ,
a
f
(
M
)
0
,
f ( M ) 0,
x1 x2 M
D 0,
a 0,
x M .
0
D 0,
x0 M ,
f ( M ) 0;
10

11. Правило 3.

Корни квадратного уравнения ax 2 bx c 0, a 0 больше
заданного числа m и меньше заданного числа М, если
имеет место сиcтема:
у
f(M)
f(m)
m х1
х0
х2 м
х
a 0,
D 0,
m x0 M ,
f ( m) 0,
f ( M ) 0,
у
m
х1
х0
f(m)
f(M)
х2
м х
a 0,
D 0,
m x0 M ,
f ( m) 0,
f ( M ) 0;
a f ( m) 0,
a f ( M ) 0,
D 0,
m x0 M .
11

12. Правило 3.

a 0,
D 0,
m x0 M ,
a f (m) 0,
f (m) 0,
a f ( M ) 0,
f ( M ) 0,
m x1 x2 M
a 0,
D 0,
m x0 M .
D
0
,
m x0 M ,
f (m) 0,
f ( M ) 0;
12

13. Правило 4.

Заданное число М лежит между корнями квадратного
уравнения ax 2 bx c 0, a 0 ,если имеет место сиcтема:
у
х1
м х0
х2
х
f(M)
у
f(M)
хх1
1
м х0
х0
х2х2 х
a 0,
f ( M ) 0;
a f ( M ) 0.
a 0,
f ( M ) 0;
13

14. Правило 4.

a 0,
f
(
M
)
0
,
x1 M x 2
a f ( M ) 0.
a 0,
f ( M ) 0;
14

15.

Задание 1 (№ 2.36(1)).
При каких значениях а корни уравнения
х2 – 2ах + (а + 1)(а – 1) = 0
принадлежат промежутку [-5;5]?
Решение.
Рассмотрим функцию f(х) = х2 – 2ах + (а + 1)(а – 1).
у
f(M)
f(m)
m х1
х0
х2 м
х
15

16.

Условию задачи удовлетворяет система
f ( m) 0,
f ( M ) 0,
D 0,
m x 0 M .
Значит,
a 4,
a 6,
25 10a (a 1)( a 1) 0,
2
a 10a 24 0,
25 10a (a 1)( a 1) 0,
a 6,
2
a 10a 24 0,
4 a 4.
2
2
a (a 1) 0,
5 a 5;
a 4,
5 a 5;
5 a 5;
Ответ: [-4;4]
16

17.

Задание 2 (№ 2.38(1)).
При каких значениях а число 1 находится между
корнями квадратного трехчлена х2 + (а + 1)х - а2 ?
Решение.
Рассмотрим функцию f(х) = х2 + (а + 1)х - а2 .
у
х1
м х0
х2
х
f(M)
Условию задачи удовлетворяет неравенство f(М) < 0.
a. 2,
2
2
1 a 1 a 0 a a 2 0
a 1.
Ответ: (−∞;−1)U(2;+∞)
17

18.

Задание 3.
При каких значениях а уравнение
х4 + (1 – 2а) х2 + а2 – 1 = 0
имеет четыре разных решения?
Решение.
х4 + (1 – 2а) х2 + а2 – 1 = 0(1)
Пусть х2 = t. Тогда уравнение (1) примет вид:
t2 + (1 – 2а)t + а2 – 1 = 0.
Первоначальное уравнение имеет четыре решения
1
> 0;
;
тогда и только тогда, когда полученное
квадратное
2
уравнение имеет два разных положительных
решения, то есть 0 < t1 < t2.
18

19.

Рассмотрим функцию
f (t ) t 2 (1 2a)t a 2 1.
у
f(M)
М х1
Имеет место система:
х0
х2
х
f ( M ) 0,
D 0,
t M .
0
a 1,
a 2 1 0,
a 1,
4
a
5
0
,
a 1,25, 1 a 1,25.
2a 1
a 0,5;
0;
2
Ответ: (1;1,25)
19

20.

Домашнее задание:
№ 2.37(1),
№ 2.40(1),
№ 2.42(1).
Спасибо за урок.
20