Similar presentations:
Лекция 1 МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
1. АЛГЕБРА
2. ГЛАВА IV. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
3. § 1. Операции над матрицами
4. § 1. Операции над матрицами
Опр 1. Прямоугольной (m n)-матрицей над полем P наз. прямоугольнаятаблица из m строк и n столбцов элементов из P, записанная виде:
11 12
22
A 21
m1 m 2
1n
2n
mn
Числа ik , где i = 1. 2,…, m; k = 1. 2,…, n, называются элементами
матрицы A.
Если m = n, то матрица A наз. квадратной матрицей порядка n.
Опр 2. Две (m n)-матрицы считаются равными тогда и только тогда, когда
равны их соответственные элементы.
Если все элементы матрицы равны нулю, то матрица называется
нулевой и обозначается буквой O.
5. § 1. Операции над матрицами
Опр. 3. Суммой двух (m n)-матриц A и B наз. такая (m n)-матрица A + B,каждый элемент которой равен сумме соответствующих элементов
матриц A и B .
Пример 1.
1 2 2 2 3 0
3
4
3
1
0
5
5 6 4 5 1 1
.
Опр. 4. Произведением (m n)-матрицы A на число наз. такая
(m n) -матрица A, каждый элемент которой равен произведению
соответственного элемента матрицы A на число .
Пример 2.
1 3 1 2 2 6 2 4
2
2
4
31
2
4
8
62
4
.
Обе эти операции бинарные, причем сложение – алг. операция на
множество M (m n,P) всех (m n)-матриц над полем P, а умножение
матриц на число - внешняя композиция, так как P, а
A M(m n,P) .
6. § 1. Операции над матрицами
Легко проверяется, что для любых (m n)-матриц A, B, C илюбых чисел , P справедливы следующие свойства:
I. Свойства операции сложения матриц
1. A + B = B + A – сложение матриц коммутативно;
2. (A + B) + C = (A + B) + C – сложение матриц ассоциативно;
3. A + O = A – существует нулевая матрица;
4. A + (-A) = O – существует противоположная матрица
–A = (-1)A.
Замечание 1. Св-ва 1 - 4 сложения матриц показывают, что
множество M(m n,P) всех (m n)-матриц над полем P
является абелевой группой относительно операции
сложения.
7. §1. Операции над матрицами
II. Свойства операции умножения матриц на число:5. 1A=A;
6. ( A)=( )A.
III. Свойства, связывающие слож. и умн. матриц на число:
7. ( + )A = A + A;
8. (A +B) = A + B.
8. § 1. Операции над матрицами
Казалось бы, естественно умножать матрицы по тому жеправилу, что и при сложении, т.е. перемножать
соответствующие элементы умножаемых матриц.
Однако, такое умножение не имеет в математике больших
приложений. Мы укажем другое правило умножения
матриц.
Дадим его сначала для квадратных матриц порядка n .
Напомним, что квадратной матрицей порядка n наз.
(m n)-матрица, т.е. матрица имеющая n строк и n столбцов.
Для квадратных матриц порядка n будем использовать
краткие обозначения:
A = ( ik) и B = ( ik ) и т.п.
9. § 1. Операции над матрицами
Опр. 5. Произведением квадратных матриц A = ( ik) и B = ( ik ) порядкаn называется квадратная матрица AB = ( ik) того же порядка n, каждый
элемент ik ( i, k = 1,2,…,n) которой, находящийся в i-ой строке и k-ом
столбце, равен сумме произведений элементов i-ой строки матрицы A
на соответственные элементы k-го столбца матрицы B, т.е.
ik= i1 1k + i2 2k +…+ in nk .
Пример 3.
3 2 1 0
1 0
1)
2 1 3 1 1 2
4 1 2 2 4 3
1 2 0 ( 1) 3 4
1 0 0 2 3 3 8 13 9
1 2 0 1 3 2
2 2 ( 1) 1 3 2 2 1 ( 1) ( 1) 3 4 2 0 ( 1) 2 3 3 9 15 7
4 2 1 1 ( 2) 2 4 1 1 ( 1) ( 2) 4 4 0 1 2 ( 2) 3 5 5 4 .
10. § 1. Операции над матрицами
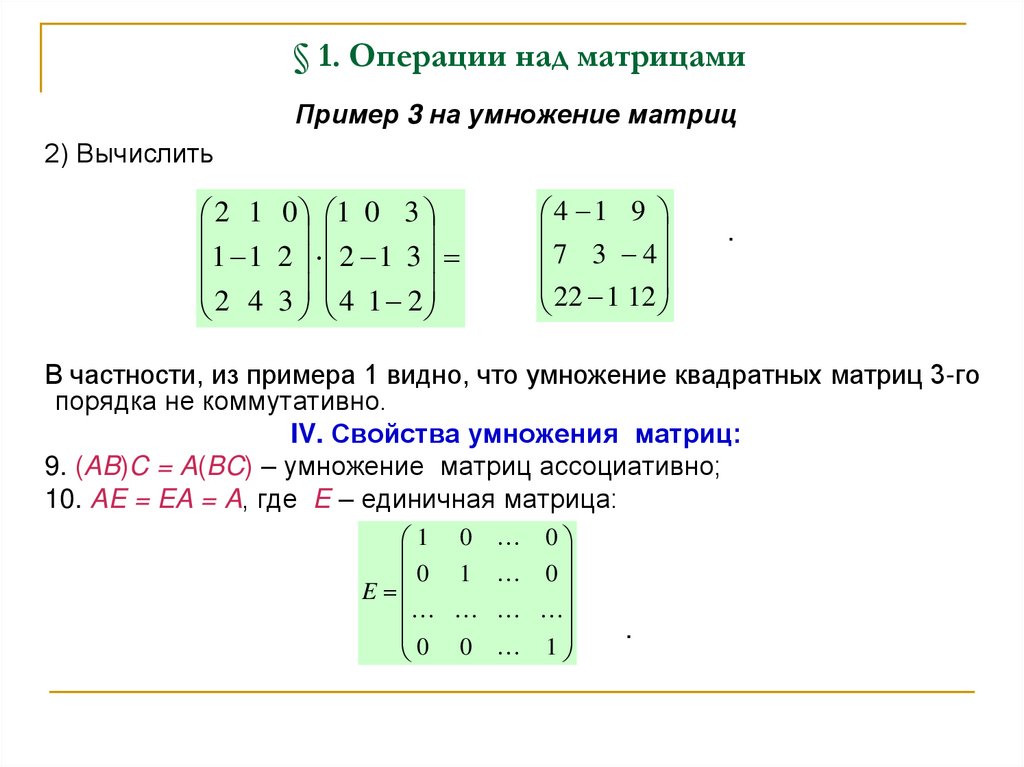
Пример 3 на умножение матриц2) Вычислить
2 1 0 1 0 3
1 1 2 2 1 3
2 4 3 4 1 2
4 1 9
7 3 4
22 1 12
.
В частности, из примера 1 видно, что умножение квадратных матриц 3-го
порядка не коммутативно.
IV. Свойства умножения матриц:
9. (AB)C = A(BC) – умножение матриц ассоциативно;
10. AE = EA = A, где E – единичная матрица:
1 0 0
0 1 0
E
0
0
1
.
11. §1. Операции над матрицами
IV. Свойства умножения матриц:11. Умножение квадратных матриц порядка n > 1 не коммутативно.
□ Обоснуем последнее свойство. Обозначим через Eik (i , k = 1. 2,…, n)
квадратную матрицу, в которой элемент, находящийся в i-ой строке и kом столбце, равен 1, а все остальные элементы равны 0.
Такие матрицы называют матричными единицами.
Нетрудно проверить следующее правило умножения матричных единиц:
Eim , если j k ;
Eij Ekm
O, если j k .
.
отсюда следует, что E12E21 = E11 E22 = E21E12. ◘
Замечание 2. Св-ва 9 - 11 умн. матриц показывают, что множество
M(n n,P) всех квадратных матриц порядка n над полем P является
моноидом, причем некоммутативным при n > 1.
В частности,
12. § 1. Операции над матрицами
.V. Свойства, связывающие умн. матриц со слож. и умн. на число:12. (A + B)C = AC+ BC, C(A + B) = CA + CB – умножение
матриц дистрибутивно относительно сложения;
13. (AB) = ( A)B = A( B) – свойство линейности
умножения.
Замечание 3. Св - ва 1 - 4 и 9 - 12 слож. и умн. матриц
показывают, что множество M(n n,P) всех квадратных
матриц порядка n над полем P является кольцом с
единицей E, причем при n > 1 некоммутативным и с
делителями нуля (напр., E11E22 = O).
13. § 1. Операции над матрицами
Опр. 6. Обратной для квадратной матрицы A порядка nназ. квадратная матрица A-1 того же порядка, для которой
A A-1 = A-1 A = E,
где E - единичная матрица.
Замечание 4. Вопрос о характеризации обратимых
матриц и способах нахождения обратных матриц будет
изложен позже. Сейчас отметим только, что множество
M(n n,P)-1 всех обратимых матриц кольца M(n n,P)
является группой, которую называют полной
линейной группой и обозначают GL(n,P).
14. § 1. Операции над матрицами
Правило умножения квадратных матриц можно распространить ина прямоугольные матрицы, если
число столбцов первого сомножителя равно числу строк
второго сомножителя.
При этом получится матрица, число строк у которой тоже, что у
первого сомножителя, а число столбцов тоже, что у второго
сомножителя.
При этом, если умножается (k m)-матрица на (m n)-матрицу, то
получится (k n)-матрица. Схематично это правило можно
изобразить так:
k m
Пример 4.
m n
=
k n
2
1 2 0 1 1 4
3 1 0 2 3 5
0
.
.
15. § 1. Операции над матрицами
В заключение этого параграфа рассмотрим еще одну унарнуюоперацию над прямоугольными матрицами.
Опр. 7. Транспонированием (m n)-матрицы A называют
переход к (n m)-матрице AT , которая получается заменой строк
матрицы A столбцами в том же порядке следования.
Матрицу AT называют транспонированной по отношению к A.
Пример 5. Eсли
2 1 4
A
3
0
5
, то
2 3
AT 1 0
4 5
.
16. § 1. Операции над матрицами
Отметим некоторые очевидные свойства операциитранспонирования, необходимые для дальнейшего. Для любых
(m n) -матриц A, B и числа из поля P имеют место свойства:
14. (A + B)T = AT + BT ;
15. ( A)T = AT ;
С помощью математической индукции можно доказать
следующее свойство, которое имеет место для любого
натурального числа n, для любых (m n)-матриц A1, A2, …, An и
чисел 1, 2, …, n :
( 1 A1 2 A2 k Ak )T 1 A1T 2 A2T k Ak T
.
Полезно иметь в виду ещё одно свойство, справедливое для
любых прямоугольных матриц A, B, для которых умножение
определено:
16. (AB)T = BTAT .
17. § 2. Определители
1. Понятие определителя2. Свойства определителя
3. Миноры и алгебраические дополнения
4. Методы вычисления определителей
18. 1. Понятие определителя
19. 1. Понятие определителя
Всякое произведение элементов матрицы11 12
22
A 21
...
...
n1 n 2
... 1n
... 2 n
... ...
... nn
,
взятых по одному и только одному из каждой строки и каждого
столбца, можно записать в виде
,
i j i j ... i j
i1
j1
i2 in
j2 jn
1 1
2 2
(1)
n n
где
– некоторая подстановка множества
{1,2,…,n}.
Ясно, что если изменить порядок сомножителей, то ни само
произведение (1), ни его подстановка не изменятся – изменится только
их запись.
В частности, различных таких произведений можно составить столько,
сколько подстановок n -ой степени, т.е. n! .
Имея это в виду, введем
20. 1. Понятие определителя
Опр. 1. Определителем квадратной матрицы A порядка nс элементами из поля P (или просто определителем n -го
порядка) называется число, равное сумме n! всевозможных
произведений элементов, взятых по одному и только одному
из каждой строки и каждого столбца матрицы , причем любое
такое произведение берется со знаком «плюс», если его
подстановка четная, и со знаком «минус», если его
подстановка нечетная.
Каждое произведение указанного выше вида вместе с его
знаком называется членом определителя.
21. Простейшие свойства определителя
Из опр. 1 вытекают следующие простейшие свойства определителя n-гопорядка.
10. Каждое произведение, входящее в определитель n-го порядка,
содержит n сомножителей.
20. Каждое произведение, входящее в определитель n-го порядка, имеет
вид
i j i j ... i j
1 1 2 2
n n
(1);
если расположить сомножители в порядке возрастания номеров строк, то
оно будет иметь вид
1k1 2 k 2 ... nk n
(2)
где k1, k2 …, kn – некоторая перестановка множества {1,2,…,n}.
30. Каждому произведению, входящему
в определитель n-го порядка,
соответствует подстановка n-ой степени , наоборот, а разным
произведениям соответствуют разные подстановки.
22. Простейшие свойства определителя
40. При n 2половина произведений, входящих в определитель
n-го порядка, берется со знаком «плюс», а половина со знаком
«минус», так как среди n! подстановок имеется n!/2 четных и n!/2
нечетных.
50. Каждый член определителя можно записать в
( 1) r 1k1 2k 2 ... nk n
где
r –
число инверсий
в перестановке
виде
,
k1, k2 …, kn.
23. Простейшие свойства определителя
Определитель матрицы обозначают det(A) или буквами , D, d и т.д.;но чаще всего пользуются обозначением |A| или в развернутом виде
11 12 ... 1n
21 22 ... 2n
...
...
n1 n 2
...
...
n1 n 2
.
Последнее обозначение хотя и громоздко, но позволяет
формулировать ряд свойств определителя без вычисления самого
определителя.
Из определения 1 вытекает, что
11 12
21 22
... ...
... nn
... 1n
... 2 n
( 1) I ( ) 1 (1) 2 ( 2) ... n ( n )
... ... S n
... nn
,
где – знак суммы, I( ) – число инверсий в перестановке .
Подчеркнем, что определитель – это число, а матрица – таблица.
24. Определители 2-го и 3-го порядков
На основании определения легко получить правилавычисления определителей 2-го т 3-го порядков:
α
α
11 12 13
21 22 23
31 32 33
α
α α α α
α
11 22 33 12 23 31 13 21 32
13 32 31 12 21 33 11 23 32
.
(правило треугольников)
Пример 1.
1
2
4
2 3
3
1
5
3
1 3 3 + 2 1 4 + 2 5 (-3) - (-3) 3 4 -1 1 5 -2 2 3 =
= 9 + 8 – 30 +36 – 5 – 12 = 53 -47 = 6.
























 mathematics
mathematics








