Similar presentations:
Математика. Место и содержание курса
1. Математика
Данчул Александр Николаевичзав. кафедрой информационных
технологий в управлении,
д.т.н., профессор
436-03-23, каб.2125 (2 корп.)
DANCH@UR.RAGS.RU
2012 г.
2. Место и содержание курса
1. Логика2. Математика
а) линейная алгебра
б) математический анализ
в) теория вероятностей
3. Основы математического моделирования
социально-экономических процессов
4. Методы принятия управленческих решений
5. Статистика
3.
ТемаЛекции Семин.
1 Матрицы и определители
4
6
2 Системы линейных алгебраических уравнений
2
6
3 Линейные пространства и преобразования
2
6
4 Функции одной переменной. Числовые последовательности. Пределы последовательностей и функций
4
4
5 Дифференциальное исчисление
4
4
6 Неопределенный и определенный интегралы
4
4
7 Ряды
4
4
8 Функции нескольких переменных
4
4
9 Случайные события
2
6
10 Случайные величины
4
4
4. Основная литература
1. Высшая математика для экономических специальностей.Учебник и Практикум (части I и II) / Под ред. Н.Ш. Кремера.
М.: Высшее образование, 2008.
2. Теория вероятностей и математическая статистика. Н.Ш.
Кремер. М.: ЮНИТИ, 2007.
5. Тема 1. Матрицы и определители Лекция 1
6. Матрицы. Определение и виды.
Опр. 1. Матрицей размера m n (m на n) называетсяпрямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа - элементы матрицы А обозначаются aij, где первый
индекс i – номер строки, а второй индекс j – номер столбца.
a11
a21
A
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
Сокращенная запись
Amn=[aij]mn или A=[aij].
j
i
aij
Пример
1 0 2
; a21 5
A23
5 4 3
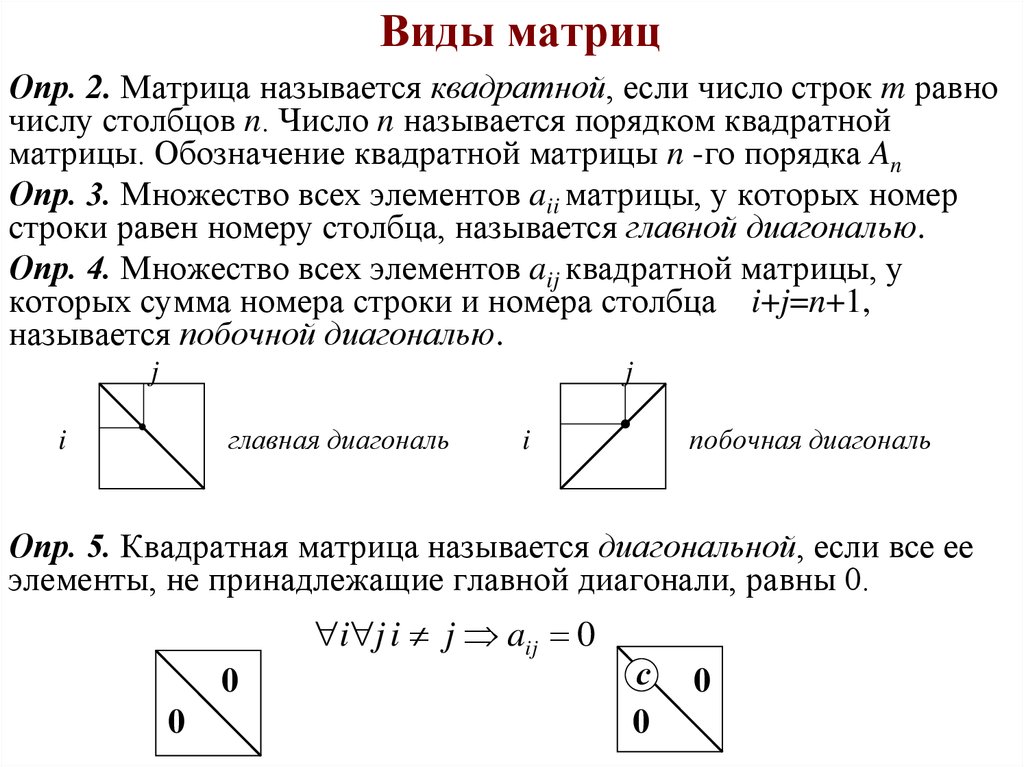
7. Виды матриц
Опр. 2. Матрица называется квадратной, если число строк m равночислу столбцов n. Число n называется порядком квадратной
матрицы. Обозначение квадратной матрицы n -го порядка An
Опр. 3. Множество всех элементов aii матрицы, у которых номер
строки равен номеру столбца, называется главной диагональю.
Опр. 4. Множество всех элементов aij квадратной матрицы, у
которых сумма номера строки и номера столбца i+j=n+1,
называется побочной диагональю.
j
j
главная диагональ
i
побочная диагональ
i
Опр. 5. Квадратная матрица называется диагональной, если все ее
элементы, не принадлежащие главной диагонали, равны 0.
i j i j aij 0
0
0
с
0
0
8. Виды матриц
Опр. 6. Диагональная матрица называется скалярной, если все ееэлементы, принадлежащие главной диагонали, равны одному и
тому же числу с.
Опр. 7. Скалярная матрица называется единичной, если все ее
элементы, принадлежащие главной диагонали, равны 1.
Обозначается Еn.
Опр. 8. Прямоугольная матрица называется нулевой, если все ее
элементы равны 0. Обозначается 0mn
1 0 0
1 0
0 0 0
;
0
Е3 = 0 1 0
0
023=
0 0 1
0 0 0
Опр. 9. Квадратная матрица называется верхней (нижней)
треугольной, если все ее элементы, находящиеся ниже (выше)
главной диагонали, равны 0.
1 3 0
1 0 0
0
*
0
2
5
3 0 0
*
0
0 0 1
4 1 2
нижняя треугольная матрица
верхняя треугольная матрица
9. Виды матриц
Опр. 10. Прямоугольная матрица называетсяверхней трапециедальной, если m<n и все ее
элементы, находящиеся ниже главной диагонали,
равны 0.
Опр. 11. Прямоугольная матрица с одним
столбцом (n=1) называется вектором-столбцом,
прямоугольная матрица с одной строкой (m=1)
называется вектором-строкой.
2
*
1 0 1
;
1 3 2
1
m
0
n
0 2 0
верхняя трапециедальная матрица
0
вектор-столбец
вектор-строка
10. Матрицы и основные операции над ними
Опр. 12. Две матрицы А и В равны, если у ниходинаковый размер и они совпадают поэлементно.
Amn Bmn i j aij bij
Df
Над матрицами определены две одноместные операции
1. Транспонирование
Строки матрицы становятся столбцами (а столбцы – строками)
с тем же номером
j
i
AT [aij ]Tmn [a ji ]nm
1 0 2
31 4
T
1 3
0 1
2 4
j
i
2. Умножение матрицы на число λ
A [aij ]mn [ aij ]mn
A ( 1) A
A
AT
1 0 2 2 0 4
2
31 4 6 2 8
11. Матрицы и основные операции над ними
Над матрицами определены три двухместные операции1. Сложение матриц
Складываются соответствующие элементы матриц
одинакового размера
[cij ]mn [aij ]mn [bij ]mn [aij bij ]mn
Df
Сложение матриц имеет те же свойства, что и сложение чисел
A+B=B+A; (A+B)+C=A+(B+C); A+0=0+A= A; A+(-A)= (-A)+A=0
2. Вычитание матриц
[cij ]mn [aij ]mn [bij ]mn [aij ]mn ( 1) [bij ]mn [aij bij ]mn
Df
1 0 2 0 3 2 1 3 4
31 4 11 5 4 2 9
1 0 2 0 3 2 1 3 0
3 1 4 1 1 5 2 0 1
12. Матрицы и основные операции над ними
3. Умножение матрицопределено, если число столбцов в первом сомножителе равно
числу строк во втором сомножителе.
Результатом умножения матрицы A размера m k на матрицу B
размера k n является матрица С размера m n , каждый
элемент cij которой равен сумме всех попарных произведений
элементов, стоящих на одинаковых
местах в i-ой строке
матрицы А и в j-ом столбце матрицы B.
k
cij ail blj ai1 b1 j ai 2 b2 j ... aik bkj
Amk ·Bkn= Cmn
1
i
m
l
k
A
ail
Df
1
l
k
х
l 1
j
j
n
B
blj
i
Σ
m
n
сij
C
13. Матрицы и основные операции над ними
Умножение матриц имеет ряд свойств, что и у умножения чисел:(A·B)·C=A·(B·C) – при соответствии размеров;
Amn·En = Em ·Amn= Amn
n
cij ail elj
Df
l 1
n
a
l 1, l j
il
elj aij e jj
n
a
l 1, l j
il
0 aij 1 aij
В то же время умножение матриц не только не всегда
возможно, но и в общем случае некоммутативно
C33= A32 · B23≠ D22= B23 · A32
Даже если умножаются квадратные матрицы A·B ≠ B·A
1
0
0
1
2 0
0 1
2 1
0 0
2 1 0 2 1
0 0 0 0 1
2 0 1 2 0
0 1 1 0 0
1 2 2 0 2
0 2 0 0 0
0 2 2 0 0
1 2 0 0 1
2
0
0
2
14. Свойства операций над матрицами
Большинство свойств (при соответствующих размерахматриц) аналогичны свойствам операций над числами:
1) A B A B B A
2) A B C A ( B C ) ( A B) C
3) A ( ) A ( A)
4) A ( ) A ( A A)
5) A B ( A B) A B
6) A B C A ( B C ) ( A B) C
сложение
умножение на
число
сложение и умножение на число
умножение
умножение и умножение на число
7) A B ( A B) ( A) B
8) A B C A ( B C ) A B A C ( A B) C A C B C
Однако в общем случае:
A B B A
сложение и умножение
15. Геометрическая интерпретация векторов
Опр. 13. Геометрическим вектором на плоскости (впространстве) с прямоугольной системой координат
называется отрезок, направленный из начала координат в
произвольную точку плоскости (пространства).
Координатами вектора называются координаты этой
точки.
Алгебраическому вектору-строке
2
ā
a = (a1, a2)
а2
(или столбцу) можно поставить в
соответствии
геометрический
вектор
а
1 1
0
на плоскости с координатами a1 и a2 .
Вектору a = (a1, a2 , a3)
сопоставляется геометрический
вектор в пространстве с
координатами a1, a2 и a3.
16. Геометрическая интерпретация векторов
Результаты операций над геометрическими векторамисоответствуют результатам операций над
соответствующими алгебраическими векторами.
a a (a1 , a2 )
a a ( a1 , a2 )
b b (b1 , b2 )
a b a b (a1 b1 , a2 b2 )
2
2
ā
а2
λа1
λā
ā+ b
а2+ b2
b2 b
0
λа2
λ<0
а1 1
а2
0
b1
1
ā
а1 а1+ b1
17. Определитель квадратной матрицы
Важнейшей числовой характеристикой квадратнойматрицы является ее определитель (детерминант).
В общем случае определитель матрицы размера n
вычисляется как составленная по определенным
правилам алгебраическая сумма n! слагаемых, каждое
из которых является произведением n элементов
матрицы, причем из каждой строки (и из каждого
столбца) матрицы входит в это произведение ровно
один элемент.
Обозначения: detA, d(A), A
Зададим правила вычислений определителей 2-го и 3-го порядка,
а затем приведем формулу для вычисления определителя
n-го порядка.
18. Определитель квадратной матрицы 1-го и 2-го порядка
n=1. A=(a11)detA= a11 = a11
n=2. Определитель равен разности произведений
элементов, стоящих на главной и побочной диагонали.
a11
a12
a21 a22
a1 a2
b1
b2
a11a22 a12a21;
3 1
1 2
1 2
3 1
+
2
3 2 1 1 5 S
1 1 3 2 5 S
2
b
S
1
0
1
ā
3
1
19. Определитель квадратной матрицы 3-го порядка
a11Определитель квадратной матрицы
3-го порядка
a12
a13
a21 a22
a23 a11a22 a33 a12 a23a31 a13a21a32
a31
a33
a32
a13a22 a31 a12 a21a33 a11a23a32
+
1
-
0 2
1 3 4 1 3 5 0 4 ( 2) 2 ( 1) 1 2 3 ( 2) 0 ( 1) 5 1 4 1
2 1 5
15 0 ( 2) ( 12) 0 4 21


















 mathematics
mathematics








