Объемы и площади поверхности многогранников и тел вращения 1

1. Тема занятия «Объемы и площади поверхности многогранников и тел вращения»

2026 г

2. Содержание

Цилиндр
Конус
Шар
Базовый уровень
(задания ЕГЭ базовый №16)
Повышенный уровень
(задания ЕГЭ профильный №8)
Высокий уровень
(задания ЕГЭ профильный №14)

3. Базовый уровень (задания ЕГЭ базовый №16)

МЕНЮ
Базовый уровень
(задания ЕГЭ базовый №16)
Vц S
б.п.ц
Старт/стоп
Vк
S
п.ш
Vш S
б.п.к

4. Объем цилиндра (Vц)

Каталог
заданий
Объем цилиндра (Vц)
Справк
а
Даны два цилиндра. Радиус основания и высота первого равны
соответственно 2 и 6, а второго — 6 и 7.
Во сколько раз объём второго цилиндра
больше объёма первого?
Решение
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма второго шара к первому:
Решение
Ответ: 10,5.
Ответ

5. Площадь боковой поверхности цилиндра (Sб.п.ц)

Каталог
заданий
Площадь боковой поверхности Справка
цилиндра (Sб.п.ц)
Даны два цилиндра. Радиус основания и высота первого равны
соответственно 4 и 18, а второго — 2 и 3.
Во сколько раз площадь боковой поверхности
первого цилиндра больше площади
боковой поверхности второго?
Решение
Площадь боковой поверхности цилиндра
находится по формуле:
Найдём Sб.п первого цилиндра:
Найдём Sб.п второго цилиндра:
Найдём отношение площади боковой поверхности
цилиндра первого цилиндра ко второму:
Решение
Ответ: 12
Ответ

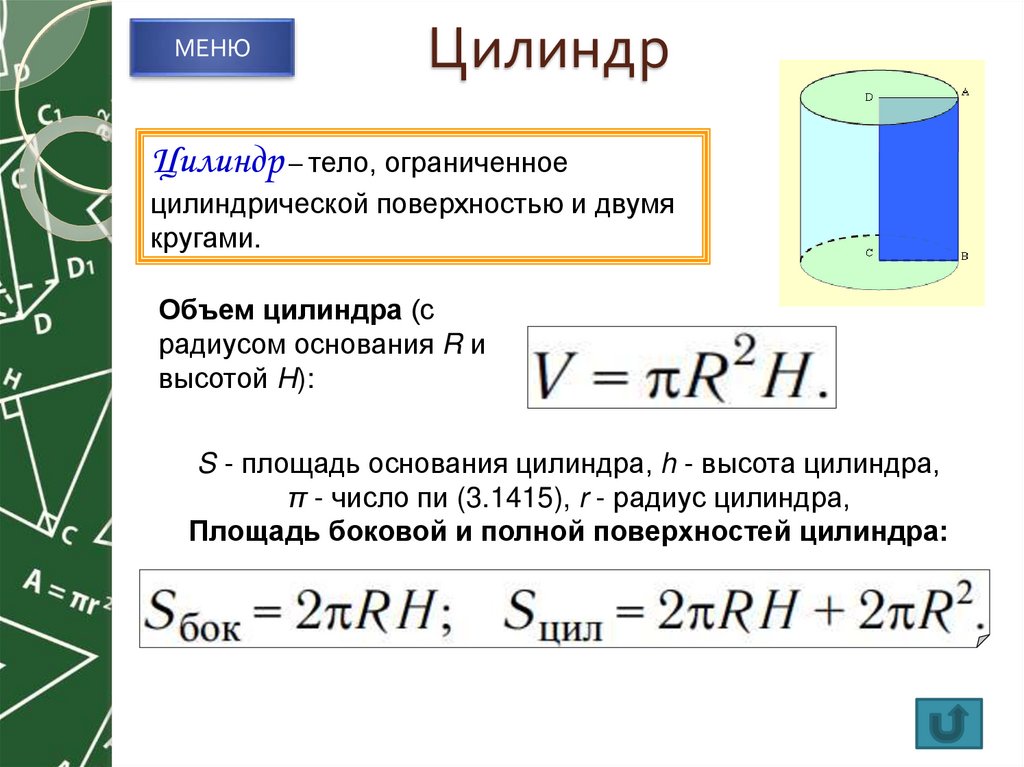
6. Цилиндр

МЕНЮ
Цилиндр
Цилиндр – тело, ограниченное
цилиндрической поверхностью и двумя
кругами.
Объем цилиндра (с
радиусом основания R и
высотой H):
S - площадь основания цилиндра, h - высота цилиндра,
π - число пи (3.1415), r - радиус цилиндра,
Площадь боковой и полной поверхностей цилиндра:

7. Объем конуса (Vк)

Каталог
заданий
Объем конуса (Vк)
Справка
Объем конуса равен 16. Через середину высоты
параллельно основанию конуса проведено
сечение, которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Решение
Меньший конус подобен большему с коэффициентом 0,5.
Объемы подобных тел относятся как куб коэффициента
подобия. Поэтому объем меньшего конуса в восемь раз
меньше объема большего конуса.
Решение
Ответ: 2.
Ответ

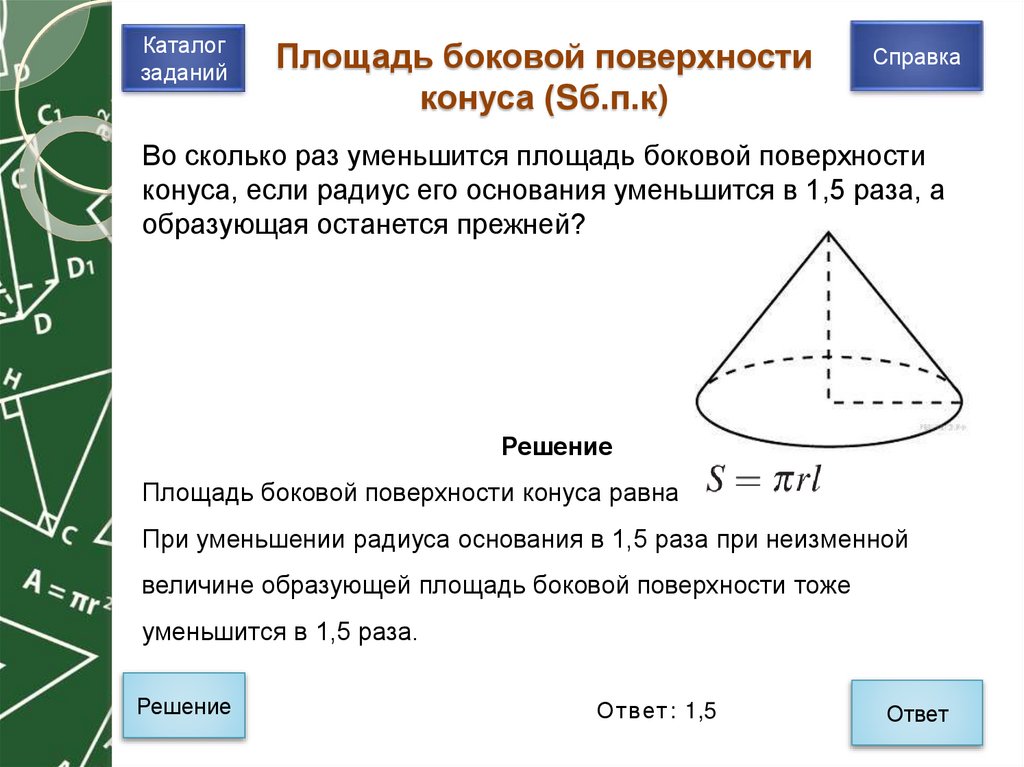
8. Площадь боковой поверхности конуса (Sб.п.к)

Каталог
заданий
Площадь боковой поверхности
конуса (Sб.п.к)
Справка
Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 1,5 раза, а
образующая останется прежней?
Решение
Площадь боковой поверхности конуса равна
При уменьшении радиуса основания в 1,5 раза при неизменной
величине образующей площадь боковой поверхности тоже
уменьшится в 1,5 раза.
Решение
Ответ: 1,5
Ответ

9. Конус

МЕНЮ
Конус
Ко́нус —
тело, которое состоит из круга –
основания конуса, точки, не лежащей в
плоскости этого круга, - вершины конуса и всех
отрезков, соединяющих вершину конуса с точками
основания.
Объем конуса (с радиусом
основания R и высотой H):
Площадь боковой поверхности конуса равна:
где R — радиус основания, l — длина образующей.

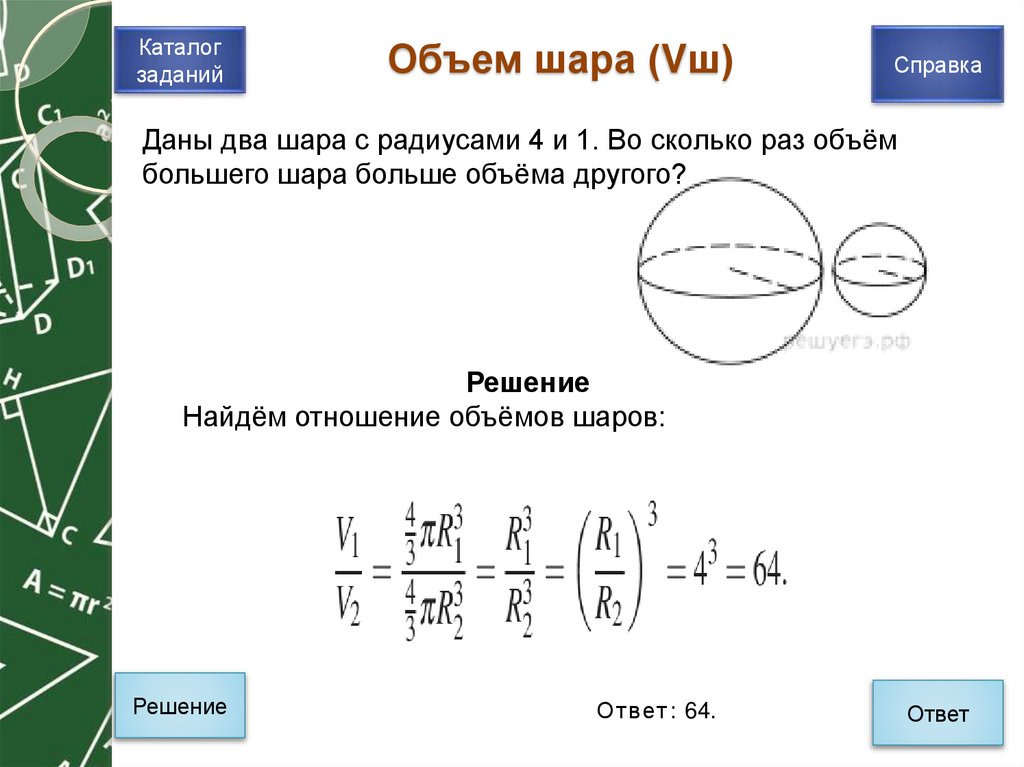
10. Объем шара (Vш)

Каталог
заданий
Объем шара (Vш)
Справка
Даны два шара с радиусами 4 и 1. Во сколько раз объём
большего шара больше объёма другого?
Решение
Найдём отношение объёмов шаров:
Решение
Ответ: 64.
Ответ

11. Площадь поверхности шара (Sш)

Каталог
заданий
Площадь поверхности
Справка
шара (Sш)
Даны два шара с радиусами 9 и 3. Во сколько раз площадь
поверхности большего шара больше площади поверхности
меньшего?
Решение
Площади шаров относятся как квадраты их радиусов,
следовательно, площадь поверхности второго шара в
раз
больше площади поверхности первого.
Решение
Ответ: 9
Ответ

12. Шар

МЕНЮ
Шар
Шар — геометрическое тело,
ограниченное поверхностью, все
точки которой отстоят на равном
расстоянии от центра. Это
расстояние называется радиусом
шара.
Объем шара (с радиусом
основания R ):
4
3
S R
3
Площадь поверхности шара:
S 4 R
2

13. Повышенный уровень (задания ЕГЭ профильный №8)

МЕНЮ
Повышенный уровень
(задания ЕГЭ профильный №8)
Vц S
б.п.ц
Старт/стоп
Vк
S
п.ш
Vш S
б.п.к

14. Объем цилиндра (Vц)

Каталог
заданий
Объем цилиндра (Vц) Справка
Шар, объём которого равен 42, вписан в цилиндр. Найдите
объём цилиндра.
Решение
Высота цилиндра равна двум радиусам вписанного в цилиндр шара, поэтому
объем цилиндра, выраженный через радиус вписанного в него шара, даётся
формулой
Объём шара вычисляется по формуле
откуда имеем:
Тем самым, объём цилиндра равен 63.
Решение
Ответ: 63
Ответ

15. Площадь боковой поверхности цилиндра (Sб.п.ц)

Каталог Площадь боковой поверхности
заданий
Справка
цилиндра (Sб.п.ц)
Длина окружности основания цилиндра равна 3,
высота равна 2. Найдите площадь
боковой поверхности цилиндра.
Решение
Площадь боковой поверхности цилиндра равна:
где C – длина окружности основания. Поэтому
Решение
Ответ: 6
Ответ

16. Объем конуса (Vк)

Каталог
заданий
Объем конуса (Vк)
Справка
Цилиндр и конус имеют общие основание и высоту.
Объём цилиндра равен 18. Найдите объём конуса.
Решение
Поскольку, конус и цилиндр имеют общую высоту и основание, имеем:
Решение
Ответ: 6.
Ответ

17. Площадь боковой поверхности конуса (Sб.п.к)

Каталог
заданий
Справка
Площадь боковой поверхности
конуса (Sб.п.к)
Длина окружности основания конуса равна 3,
образующая равна 2. Найдите площадь
боковой поверхности конуса.
Решение
Площадь боковой поверхности конуса равна
,
где С — длина окружности основания, а l — образующая. Тогда
Ответ: 3
Решение
Ответ

18. Объем шара (Vш)

Каталог
заданий
Объем шара (Vш)
Справка
Цилиндр описан около шара. Объем цилиндра равен 33.
Найдите объем шара.
Решение
Выразим из формулы для объёма цилиндра
подставим в формулу для объёма шара
Решение
Ответ: 22
и
Ответ

19. Домашнее задание: Площадь поверхности шара (Sш)

Каталог
заданий
Домашнее задание:
Площадь поверхности
шара (Sш)
Справка
Даны два шара. Радиус первого шара в 2 раза
больше радиуса второго. Во сколько раз площадь
поверхности первого шара больше площади
поверхности второго?