Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет

1.

Конусом называется фигура, полученная
при вращении прямоугольного
треугольника вокруг оси, содержащей его
катет.
Sбок rl
Sполн r rl
2
1
1 2
V Sоснh r h
3
3
21.10.2021
1

2.

Площади подобных фигур относятся
как коэффициент подобия в квадрате.
Объемы подобных фигур относятся
как коэффициент подобия в кубе.
21.10.2021
2

3.

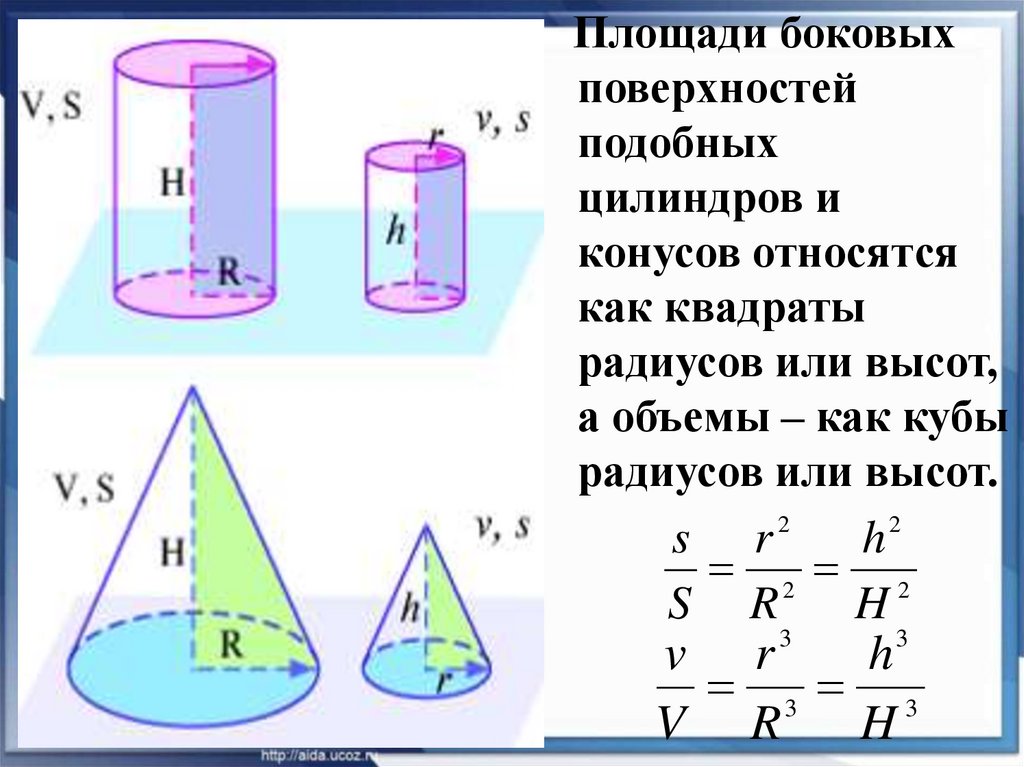
Площади боковых
поверхностей
подобных
цилиндров и
конусов относятся
как квадраты
радиусов или высот,
а объемы – как кубы
радиусов или высот.
2
2
s r
h
2 2
S R
H
3
3
v r
h
3 3
V R
H

4. Площадь боковой поверхности конуса равна 48π, а площадь основания равна 36π. Найдите длину образующей конуса.

21.10.2021
4

5.

Площадь боковой поверхности конуса равна 48π, а площадь боковой
поверхности усеченного конуса с такими же основанием и углом
наклона образующей к плоскости основания равна 36π. Найдите
высоту усеченного конуса, если высота исходного конуса равна 10.
21.10.2021
5

6.

• Высота конуса равна 15, а диаметр
основания – 16. Найдите образующую
конуса.
21.10.2021
6

7.

. Длина окружности основания конуса равна
образующая равна Найдите площадь боковой поверхности конуса.
• Длина окружности основания конуса
равна 5, образующая равна 8. Найдите
площадь боковой поверхности конуса.
21.10.2021
7

8.

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?
• Во сколько раз увеличится площадь
боковой поверхности конуса, если его
образующую увеличить в 9 раз?
21.10.2021
8

9.

Во сколько раз увеличится объем конуса, если
радиус его основания увеличится в 17 раз,
а высота останется прежней?
21.10.2021
9

10.

• Площадь полной поверхности конуса
равна 148. Параллельно основанию конуса
проведено сечение, делящее высоту
пополам. Найдите площадь полной
поверхности отсеченного конуса.
21.10.2021
10

11.

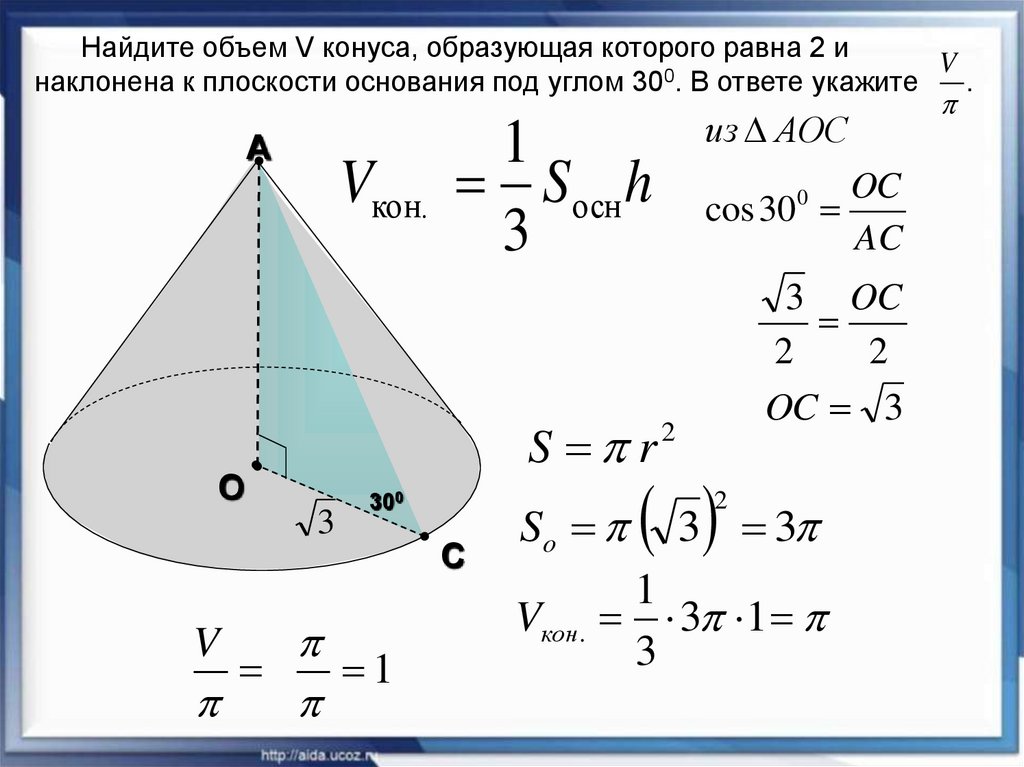
Найдите объем V конуса, образующая которого равна 2 и
V
0
наклонена к плоскости основания под углом 30 . В ответе укажите
.
А
Vкон.
S r
О
3
300
1
V
из АОС
1
S осн h
3
С
So
Vкон.
OC
cos 30
AC
0
3 OC
2
2
OC 3
2
3 3
2
1
3 1
3

12.

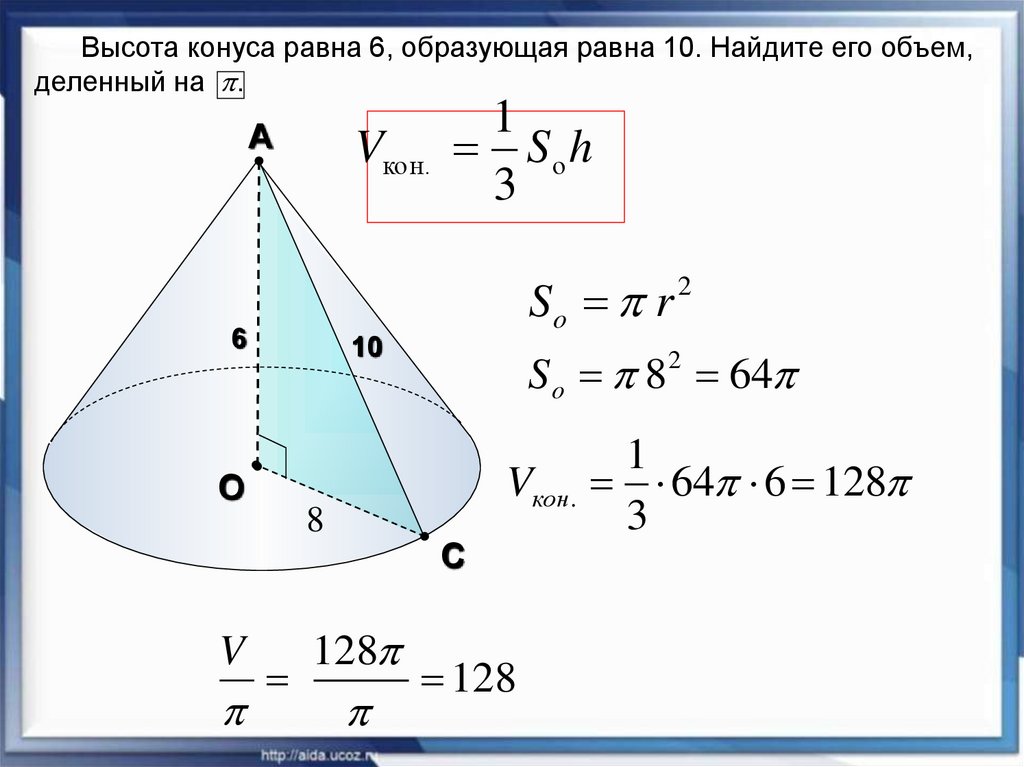
Высота конуса равна 6, образующая равна 10. Найдите его объем,
деленный на .
А
Vкон.
So r
6
10
О
V
1
Sо h
3
S o 8 64
2
Vкон.
8
С
128
2
128
1
64 6 128
3

13.

Конус получается при вращении равнобедренного прямоугольного
треугольника АВС вокруг катета, равного 6. Найдите его объем,
деленный на .
Vкон.
А
1
Sо h
3
So r 2
6
S o 6 36
1
Vкон. 36 6 72
3
2
В
С
V
72
72

14.

Объем конуса равен 16. Через середину высоты параллельно
основанию конуса проведено сечение, которое является
основанием меньшего конуса с той же вершиной. Найдите
объем меньшего конуса.
Решение:
1
k
2
Конусы подобны
Vм 1
Vб
2
3
Vм
1
16 1
Vм
2
16
8
8
Ответ: 2

15.

Во сколько раз уменьшится объем конуса, если его высота
уменьшится в 3 раза, а радиус основания останется
прежним?
Решение:
3h
r
h
r
1 2
V1 r 3 h
3
1 2
V2 r h
3
Составим отношение:
1
r 2 3h
V1
3
3
в три раза
1
V2
1
r 2 h
3
Ответ: 3
Чунин Павел 11«А»

16.

Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 5 раз?
1
Sо h
5
V1
3
V2 1 S 1 h 1
о
3 5
V1
h
1
V = SoH
3
1
h
5
О
V2
r

17.

Во сколько раз увеличится объем конуса, если радиус его
основания увеличится в 1,5 раза, а высота останется
прежней?
h
h
r
1,5 r
Решение:
1 2
V1 r h
3
1
V2 ( 1,5 r )2 h
3
Составим отношение:
1
r 2 h
3
V1
1
в 2,25 раза
1
V2
2 ,25 r 2 h 2 ,25
3
Ответ: 2 ,
2 5

18.

Во сколько раз увеличится площадь боковой поверхности
конуса, если его образующая увеличится в 3 раза, а радиус
основания останется прежним?
Решение:
Sбок 1 rl
3l
Sбок 2 r 3l
l
r
r
Составим отношение:
Sбок 1
rl
1
Sбок 2
r 3 l
3
Ответ: 3
в три раза

19.

Во сколько раз увеличится объём конуса, если радиус его основания
увеличить в 8 раз, а высоту оставить прежней?
21.10.2021
19

20.

Площадь боковой поверхности конуса в два раза больше
площади основания. Найдите угол между образующей
конуса и плоскостью основания.
21.10.2021
20

21. Площадь основания конуса равна 36 π, высота – 10. Найти площадь осевого сечения этого конуса.

21.10.2021
21

22.

Площадь полной поверхности конуса равна 12. Параллельно
основанию конуса проведено сечение, делящее высоту
пополам. Найдите площадь полной поверхности отсеченного
конуса.
Решение:
k
Конусы подобны
Sм
1
Sб
2
Sм
1
12
4
Ответ: 3
Sм
1
2
2
12 1
3
4

23. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.

21.10.2021
23

24.

Конус и цилиндр имеют общее основание и общую высоту
(конус вписан в цилиндр). Вычислите объём конуса, если объём
цилиндра равен 150.
Решение:
Vц r 2 h
h
h
1 2
Vк r h
3
r
Составим отношение:
Vц
r 2 h
1
3
150
3
Vк 150 1 50
1 2
1
Vк
1
Vк
1
3
r h
3
3
Ответ: 5 0

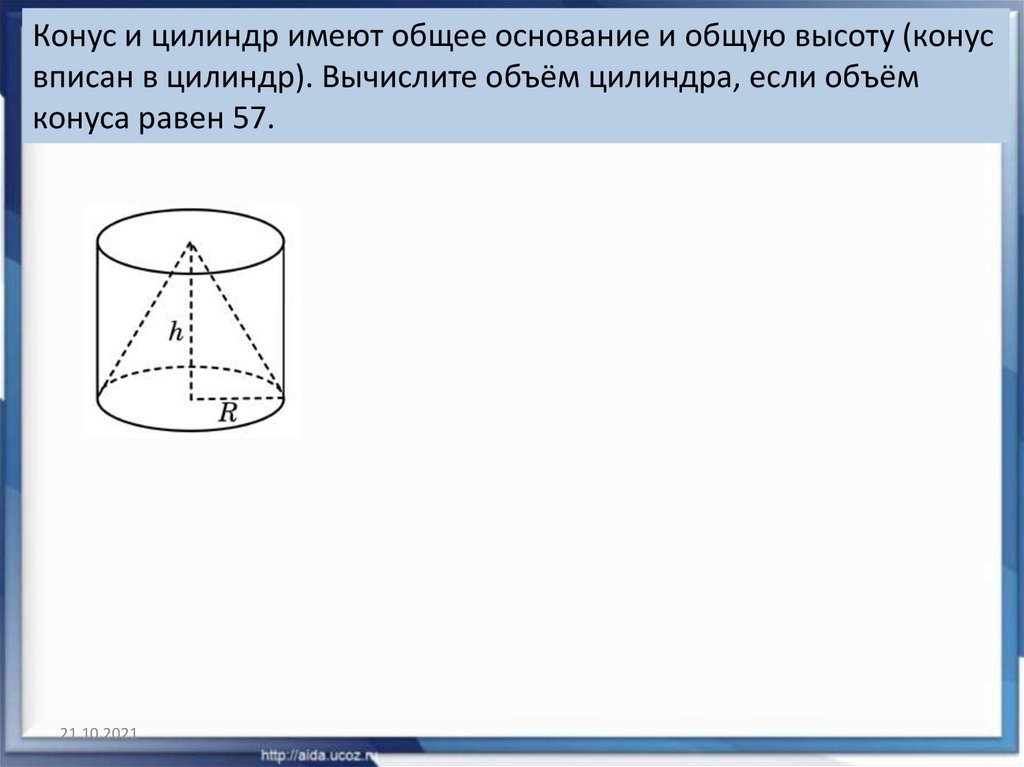
25. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса

равен 25.
Решение:
Vк
1
R 2 h
3
Vц R 2 h
Составим отношение объема конуса к объему цилиндра.
1
R2 h
Vк
1
3
2
Vц
R h
3
25
1
Vц
3
25 3
Vц
75
1
Ответ:
21.10.2021
7 5
25

26. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Причем радиус основания равен высоте. Найдите

площадь боковой поверхности цилиндра, если площадь
боковой поверхности конуса равна 7√2.
21.10.2021

27. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса

равен 57.
21.10.2021

28.

Площадь основания конуса равна 48. Плоскость,
параллельная плоскости основания конуса, делит
его высоту на отрезки длиной 15 и 45 считая от
вершины. Найдите площадь сечения конуса этой
плоскостью.
21.10.2021
28

29.

Площадь полной поверхности конуса равна 50.
Параллельно основанию конуса проведено сечение,
делящее высоту в отношении 3:2, считая от вершины
конуса. Найдите площадь полной поверхности
отсечённого конуса.
21.10.2021
29

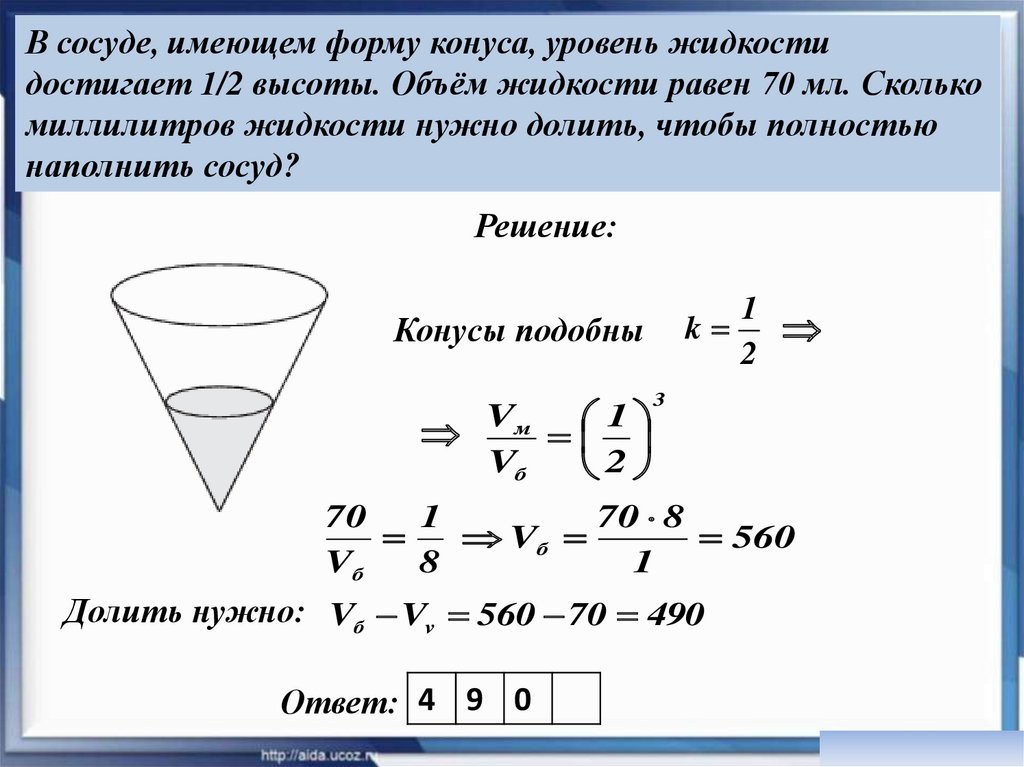
30.

В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
Решение:
k
Конусы подобны
Vм 1
Vб
2
1
2
3
70 8
70
1
Vб
560
1
Vб
8
Долить нужно: Vб Vv 560 70 490
Ответ: 4 9 0

31.

В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 54 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?

32.

В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 25
мл.Сколько миллилитров жидкости нужно долить, чтобы
полностью наполнить сосуд?

33.

В сосуде, имеющем форму конуса, уровень жидкости
достигает 2/3 высоты. Объём жидкости равен 16
мл.Сколько миллилитров жидкости нужно долить, чтобы
полностью наполнить сосуд?