Решение задач на нахождение объемов тел вращения

1.

Практическое занятие
Тема. Решение задач на
нахождение объемов тел
вращения
© Фокина Лидия Петровна

2. Указания к выполнению заданий

• С презентацией необходимо работать в режиме
демонстрации, тогда гиперссылки будут активны.
• К каждой задаче есть подсказки в виде чертежей,
формул и ответа для самопроверки.
• Рекомендовано решить 10 задач на ваш выбор +3
как ДЗ, оформить их в соответствии требований.
• Фотоотчет выполненных заданий + дз присылать на
электронный адрес [email protected] с пометкой
«14.05_ФИ_ 11» до начала следующего занятия.
• Внимание! 17.05 контрольная работа по теме!
© Фокина Лидия Петровна

3.

© Фокина Лидия Петровна

4. Содержание

1
2
3
4
5
6
7
8
9
10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26
© Фокина Лидия Петровна
27

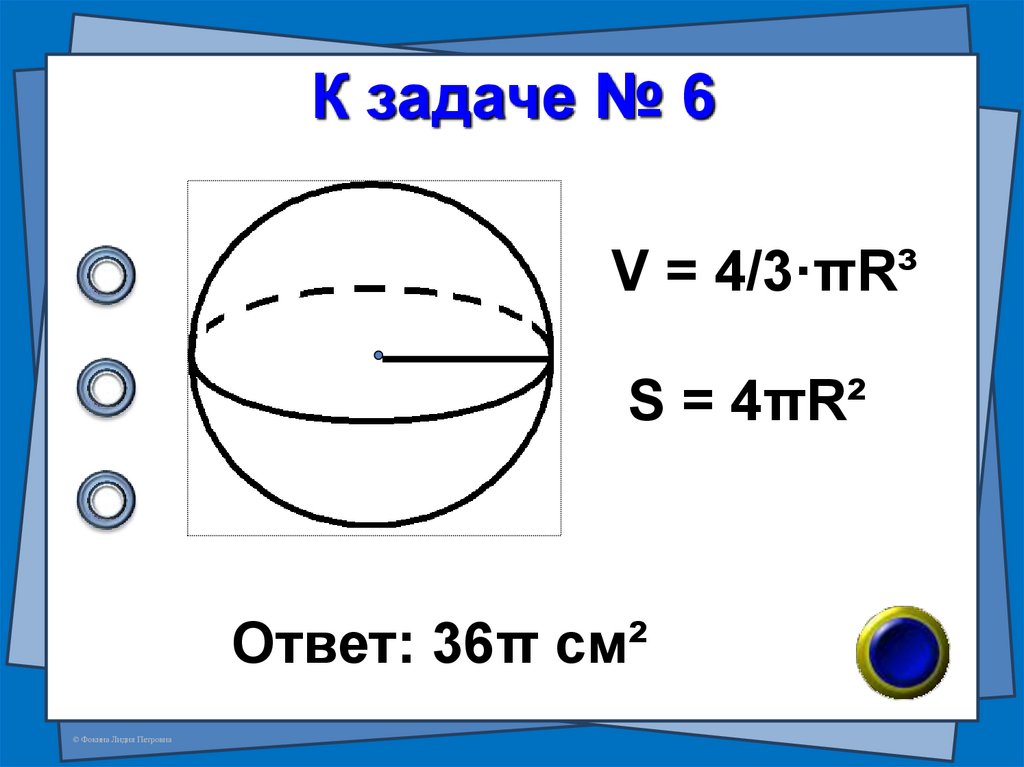
5. В-25 №7 Объём шара равен 36π см³. Найдите площадь поверхности шара.

№6
В-25 №7
Объём шара равен
36π см³. Найдите площадь
поверхности шара.
© Фокина Лидия Петровна

6. К задаче № 6

V = 4/3·πR³
S = 4πR²
Ответ: 36π см²
© Фокина Лидия Петровна

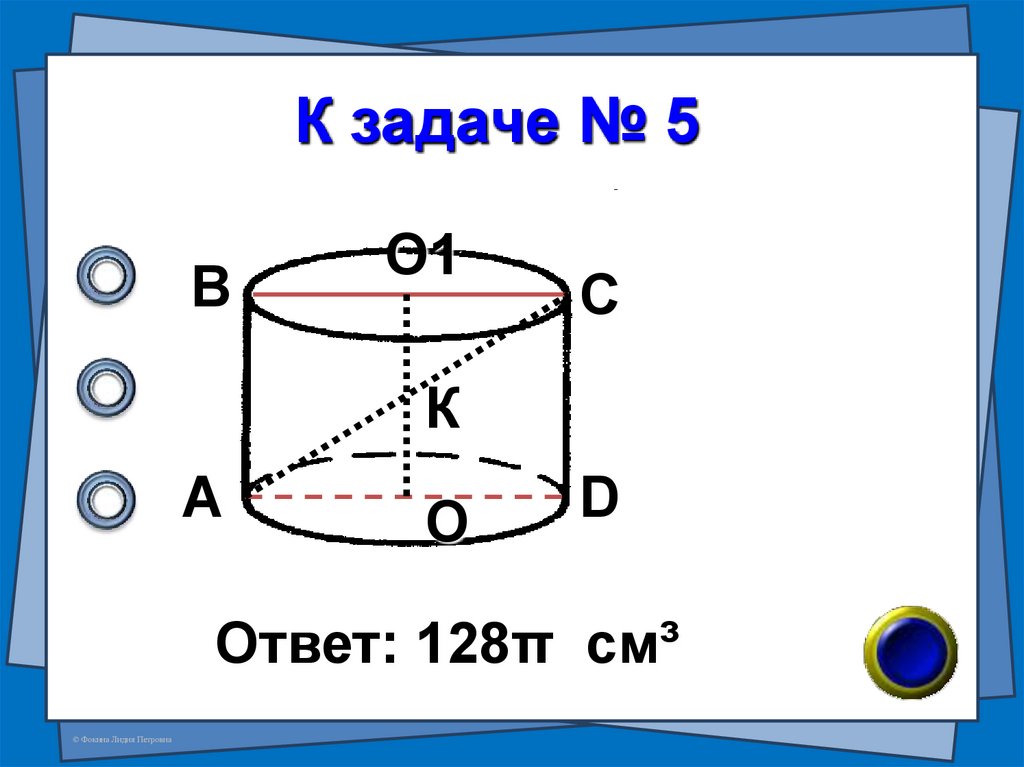
7. № 5 (В-18 №7)

Осевым сечением цилиндра
является квадрат,
диагональ которого равна
8√2 см.Найдите объем
цилиндра.
© Фокина Лидия Петровна

8. К задаче № 5

В
О1
С
К
А
О
D
Ответ: 128π см³
© Фокина Лидия Петровна

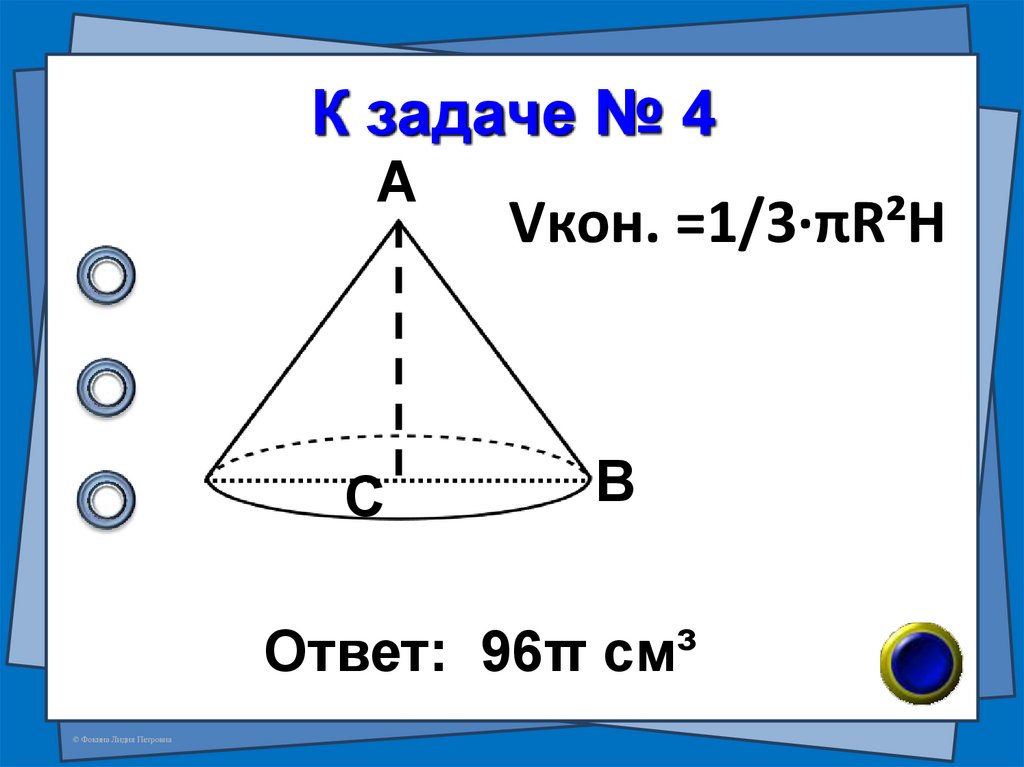
9. №4 (В-13 №7)

Найдите объём тела,
полученного при вращении
прямоугольного треугольника
с катетом 6см и гипотенузой
10см вокруг большего катета.
© Фокина Лидия Петровна

10. К задаче № 4

А
С
Vкон. =1/3·πR²H
В
Ответ: 96π см³
© Фокина Лидия Петровна

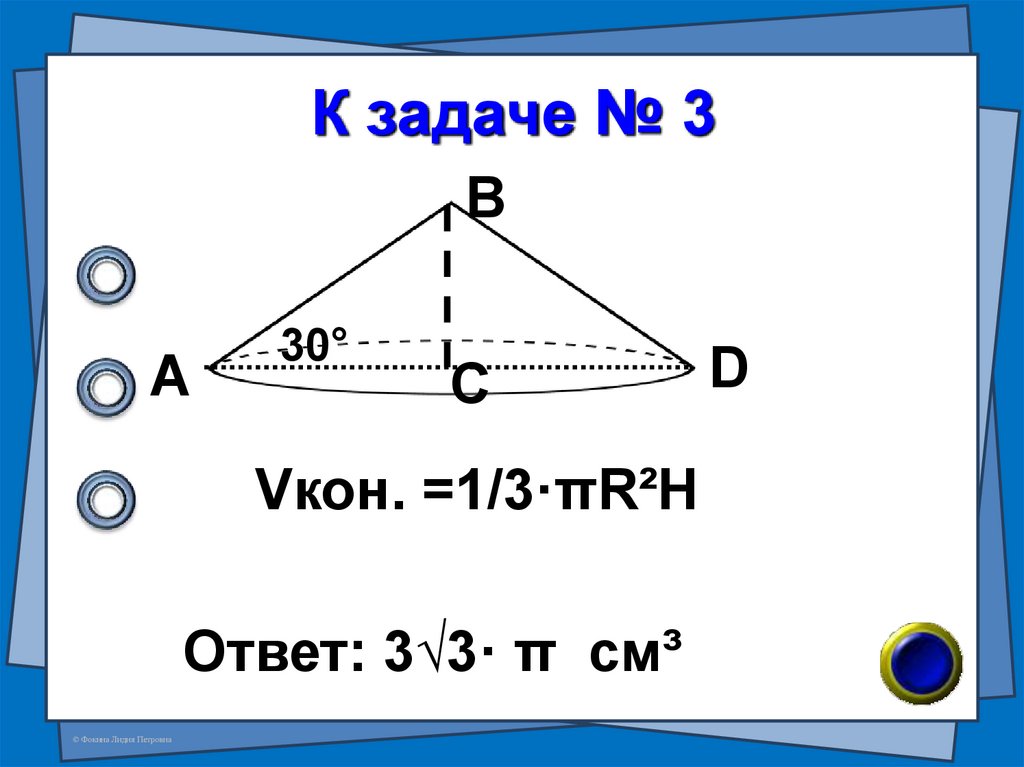
11. № 3 (В-9 №7)

Найдите объём тела,
полученного при вращении
прямоугольного треугольника
с катетом 3см и прилежащим
углом 30° вокруг меньшего
катета.
© Фокина Лидия Петровна

12. К задаче № 3

В
А
30°
С
Vкон. =1/3·πR²H
Ответ: 3√3· π см³
© Фокина Лидия Петровна
D

13. № 2 (В-4 №7)

Радиус основания цилиндра
равен 4см, площадь
боковой поверхности
вдвое больше площади
основания. Найдите объём
цилиндра.
© Фокина Лидия Петровна

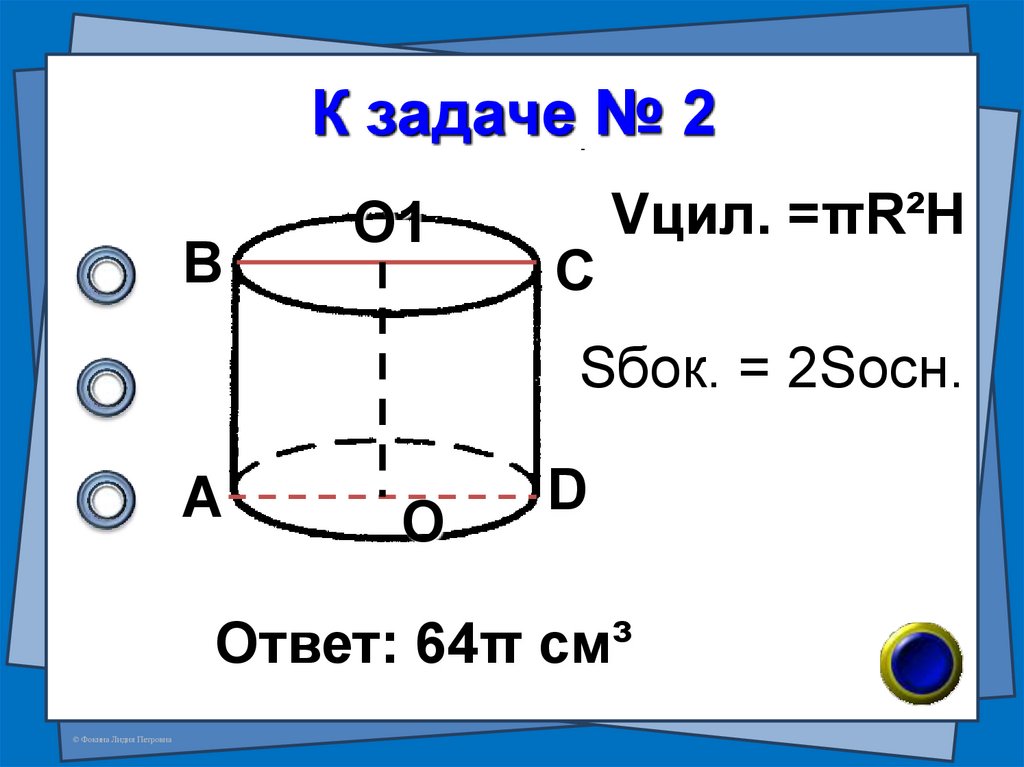
14. К задаче № 2

В
О1
С
Vцил. =πR²H
Sбок. = 2Sосн.
А
О
D
Ответ: 64π см³
© Фокина Лидия Петровна

15. № 1

№1
Равнобедренная трапеция,
основания которой равны
6 см и 10 см, а острый угол 60°,
вращается вокруг большего
основания. Найдите объем
тела вращения.
© Фокина Лидия Петровна

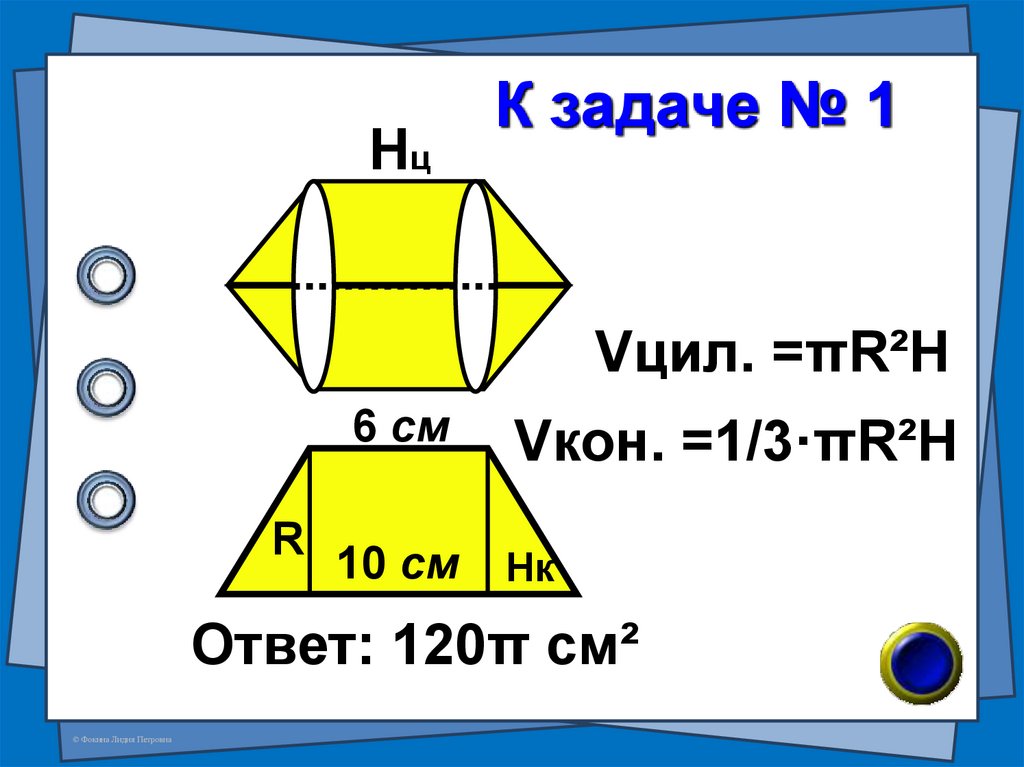
16. К задаче № 1

Hц
К задаче № 1
Vцил. =πR²H
R
6 см
Vкон. =1/3·πR²H
10 см
Hк
Ответ: 120π см²
© Фокина Лидия Петровна

17. № 8 (В-31 №7)

Площадь боковой поверхности
конуса равна 20π см², а
площадь его основания на
4π см² меньше. Найдите
объём конуса.
© Фокина Лидия Петровна

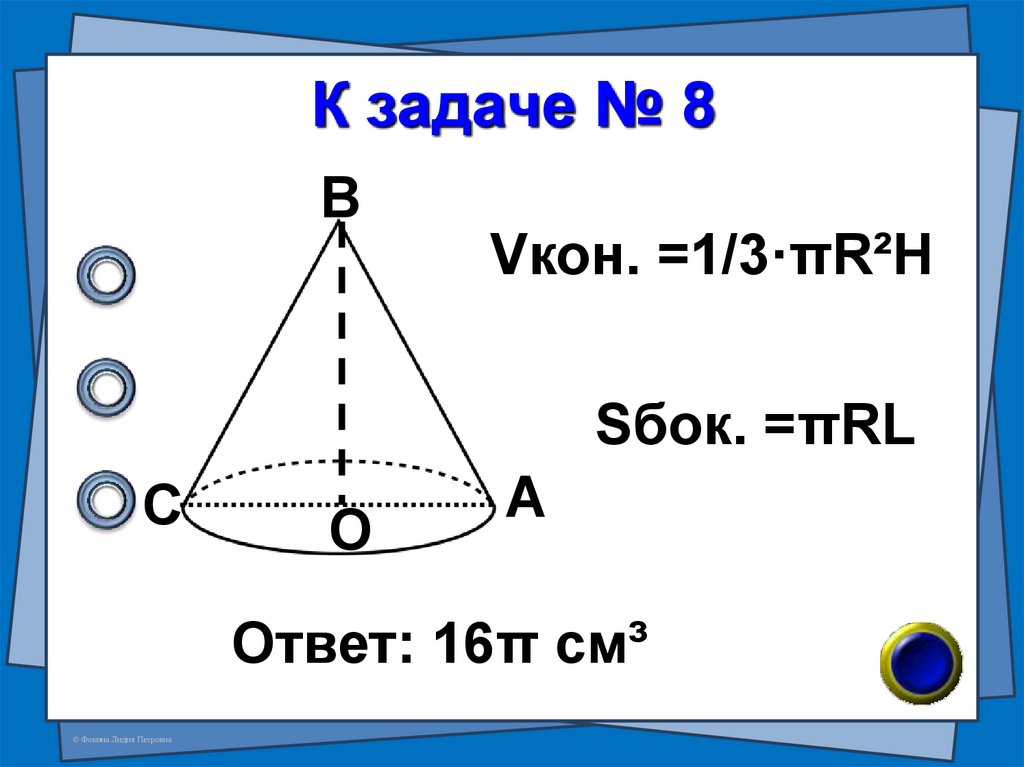
18. К задаче № 8

В
Vкон. =1/3·πR²H
Sбок. =πRL
С
О
А
Ответ: 16π см³
© Фокина Лидия Петровна

19. № 16 (В-63 №7)

Высота цилиндра равна 6см, а
его площадь боковой
поверхности вдвое меньше
площади его полной
поверхности. Найдите объём
цилиндра.
© Фокина Лидия Петровна

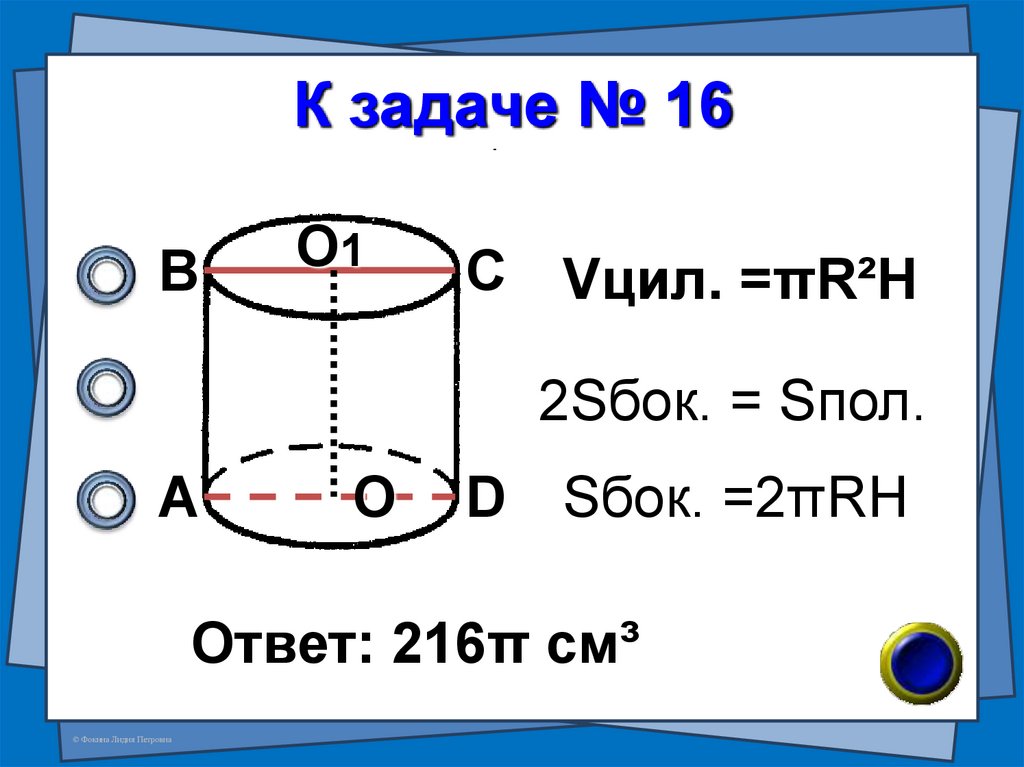
20. К задаче № 16

В
О1
С Vцил. =πR²H
2Sбок. = Sпол.
А
О
D Sбок. =2πRH
Ответ: 216π см³
© Фокина Лидия Петровна

21. № 15 (В-62 №7)

Образующая конуса равна
5см, а площадь его
боковой поверхности
равна 15π². Найдите
объём конуса.
© Фокина Лидия Петровна

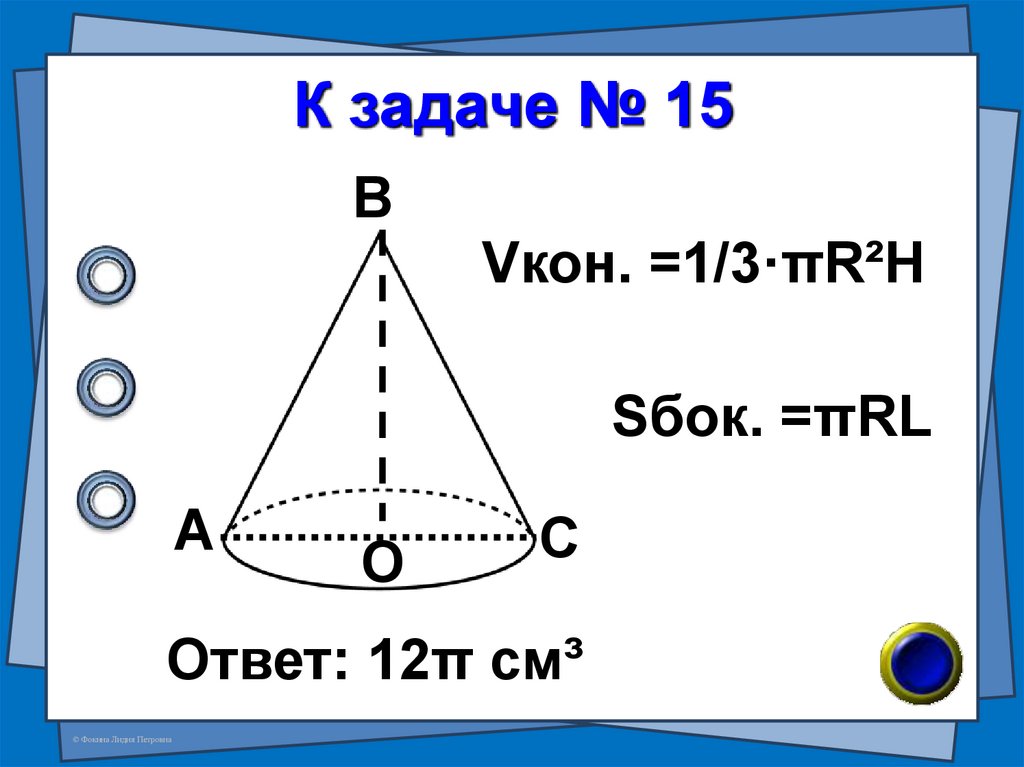
22. К задаче № 15

В
Vкон. =1/3·πR²H
Sбок. =πRL
А
О
С
Ответ: 12π см³
© Фокина Лидия Петровна

23. № 14 (В-60 №7)

Радиус основания конуса
равен 5 см, а образующая
конуса равна 13 см.
найдите объём конуса.
© Фокина Лидия Петровна

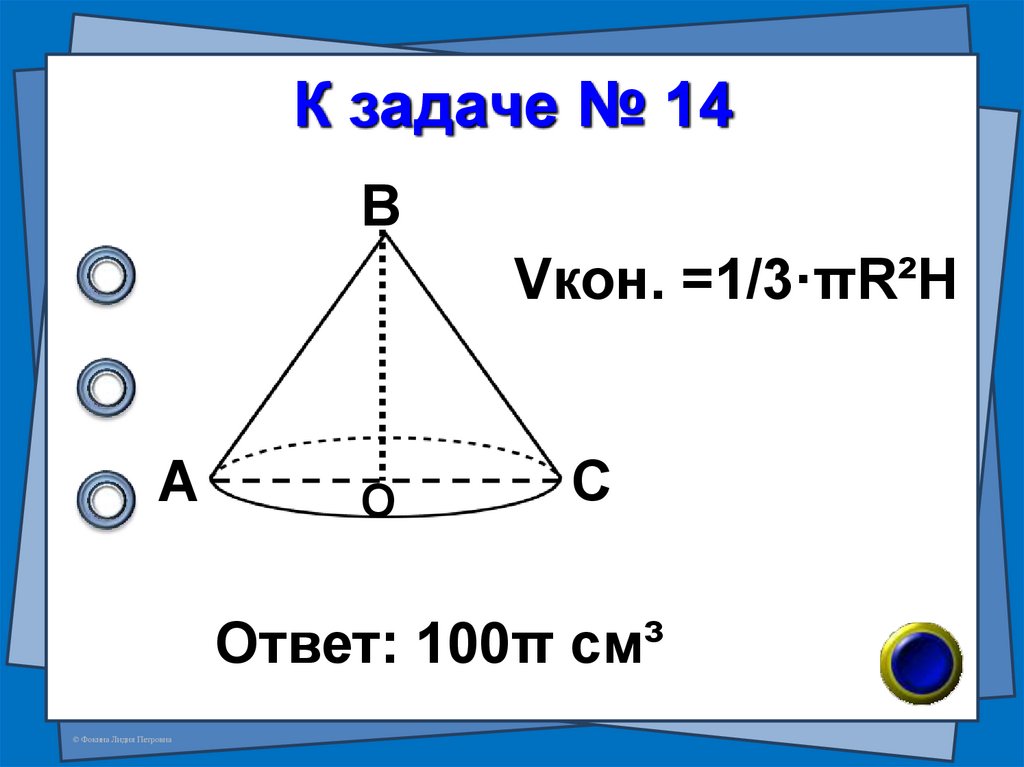
24. К задаче № 14

В
Vкон. =1/3·πR²H
А
О
С
Ответ: 100π см³
© Фокина Лидия Петровна

25. № 13 (В-51 №7)

Найдите объём тела,
полученного при вращении
прямоугольного треугольника
с гипотенузой 10см и острым
углом 30° вокруг меньшего
катета.
© Фокина Лидия Петровна

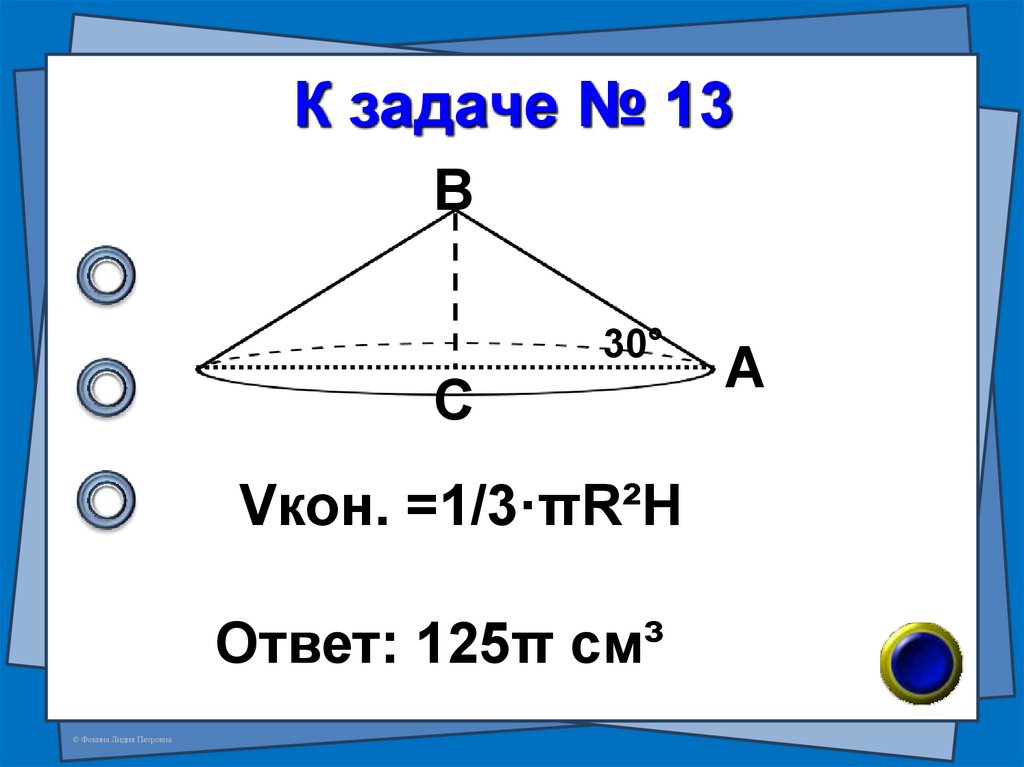
26. К задаче № 13

В
30°
С
Vкон. =1/3·πR²H
Ответ: 125π см³
© Фокина Лидия Петровна
А

27. № 12 (В-48 №7)

Найдите объём тела,
полученного при
вращении прямоугольника
со сторонами 6см и 10см
вокруг большей стороны.
© Фокина Лидия Петровна

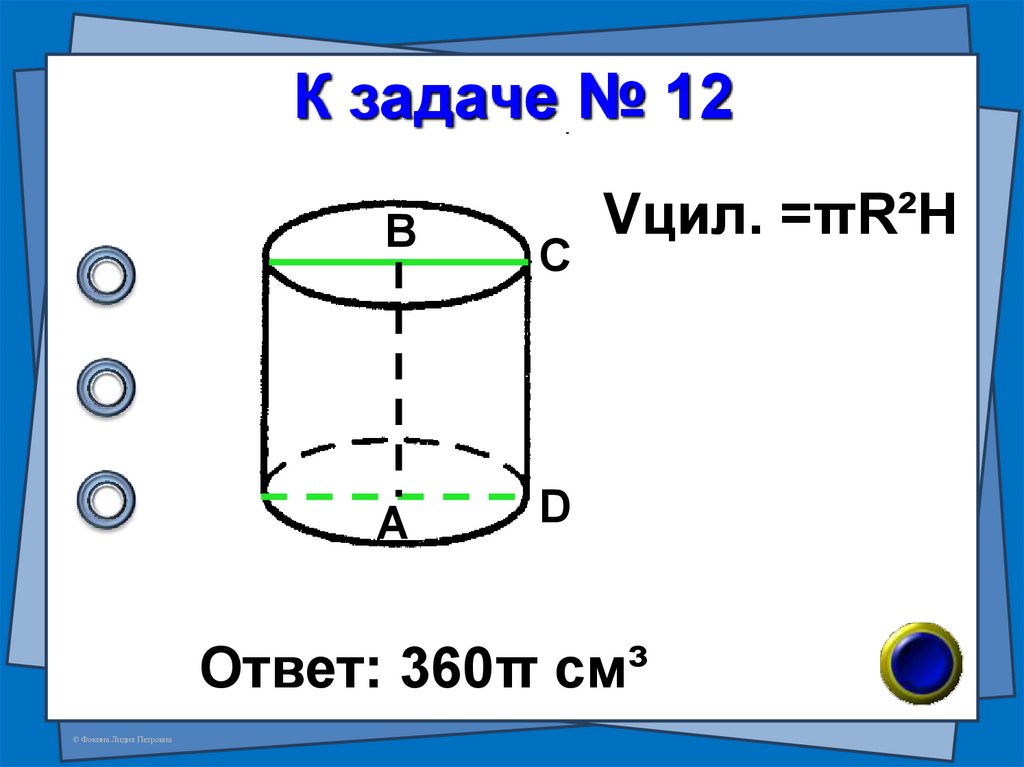
28. К задаче № 12

В
А
С
Vцил. =πR²H
D
Ответ: 360π см³
© Фокина Лидия Петровна

29. № 11 (В- 41 №7)

Найдите объём тела,
полученного при вращении
прямоугольника со сторонами
4см и 6см вокруг прямой,
проходящей через середины
его больших сторон.
© Фокина Лидия Петровна

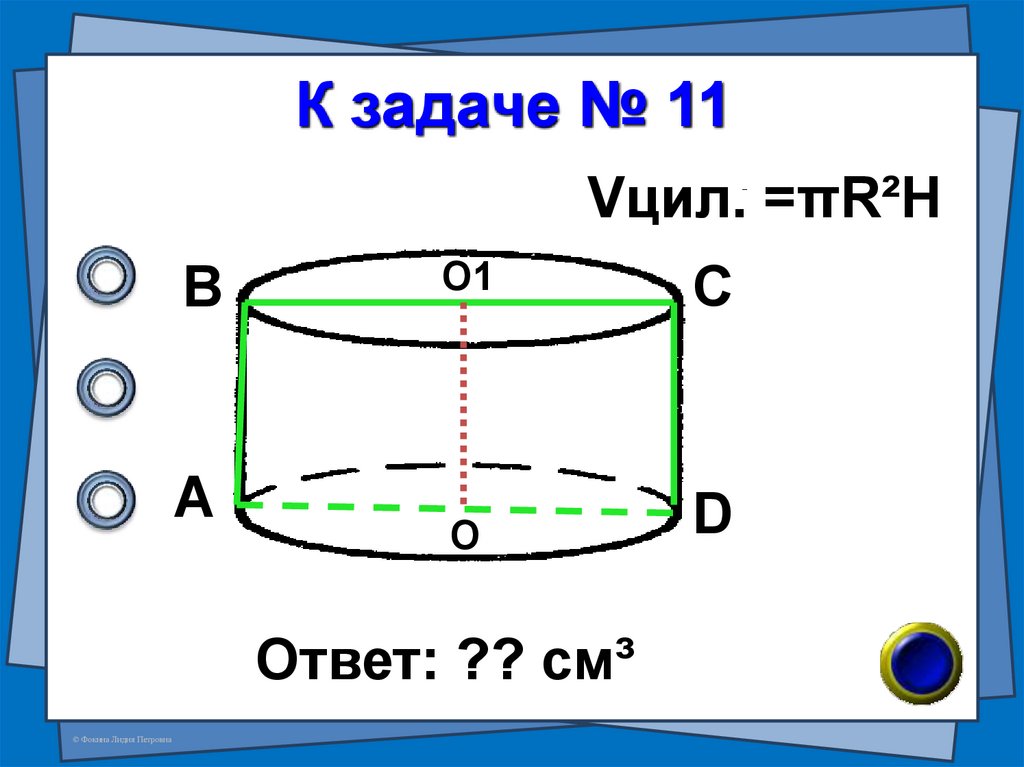
30. К задаче № 11

Vцил. =πR²H
В
А
О1
С
О
D
Ответ: ?? см³
© Фокина Лидия Петровна

31. № 10 (В – 37 №7)

Радиус основания цилиндра
равен 8см, площадь
боковой поверхности
вдвое меньше площади
основания. Найдите объём
цилиндра.
© Фокина Лидия Петровна

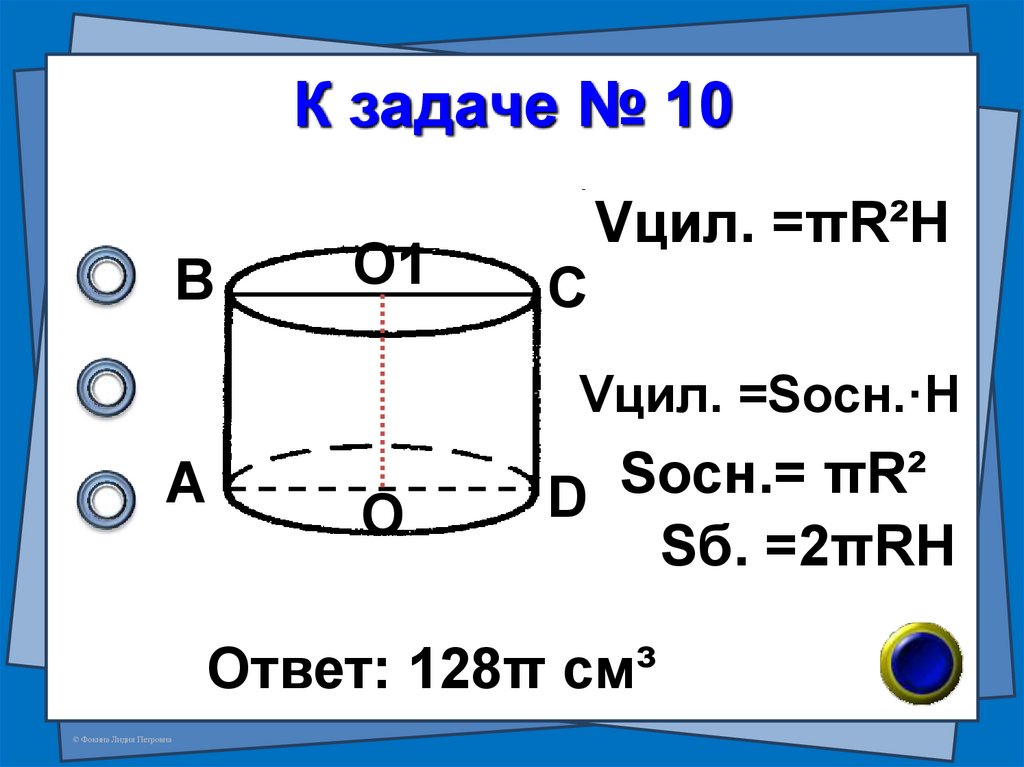
32. К задаче № 10

В
О1
Vцил. =πR²H
С
Vцил. =Sосн.·H
А
О
Sосн.=
πR²
D
Sб. =2πRH
Ответ: 128π см³
© Фокина Лидия Петровна

33. (В-29 №7) Образующая конуса равна 12 см и составляет с плоскостью основания угол в 30°. Найдите объём конуса.

№ 7 (В-29 №7)
Образующая конуса равна
12 см и составляет с
плоскостью основания
угол в 30°. Найдите объём
конуса.
© Фокина Лидия Петровна

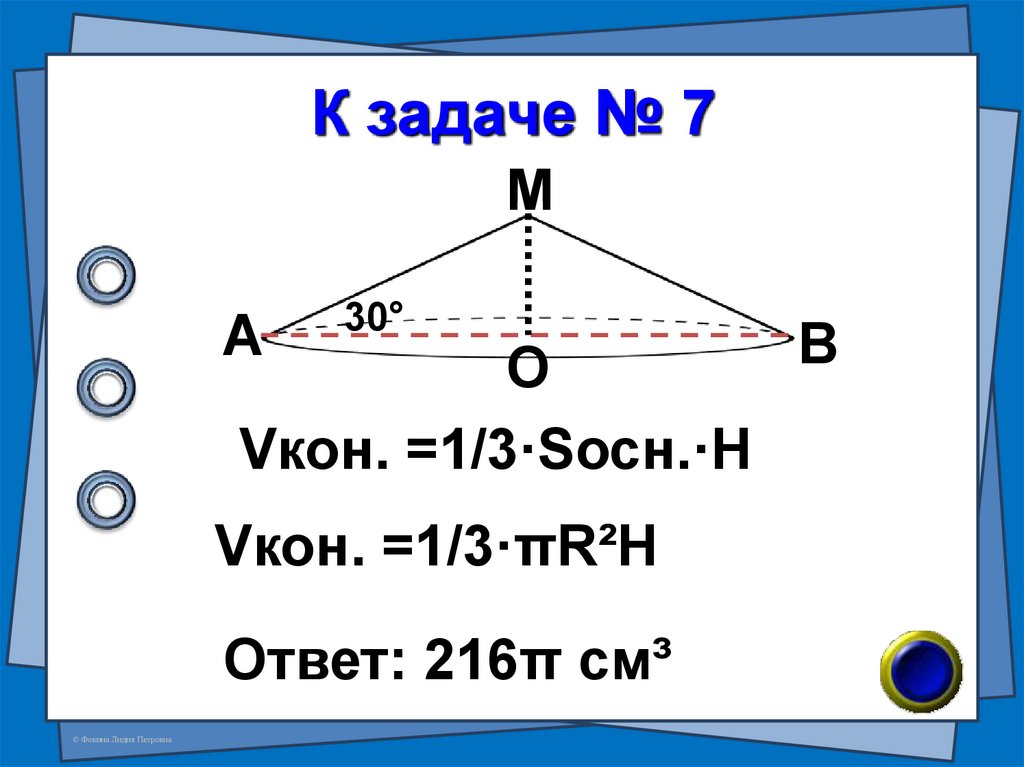
34. К задаче № 7

М
А
30°
О
Vкон. =1/3·Sосн.·H
Vкон. =1/3·πR²H
Ответ: 216π см³
© Фокина Лидия Петровна
В

35. (В-32 №7) Объём конуса с радиусом 6 см равен 96π см³. Найдите площадь боковой поверхности конуса.

№9
(В-32 №7)
Объём конуса с радиусом
6 см равен 96π см³.
Найдите площадь
боковой поверхности
конуса.
© Фокина Лидия Петровна

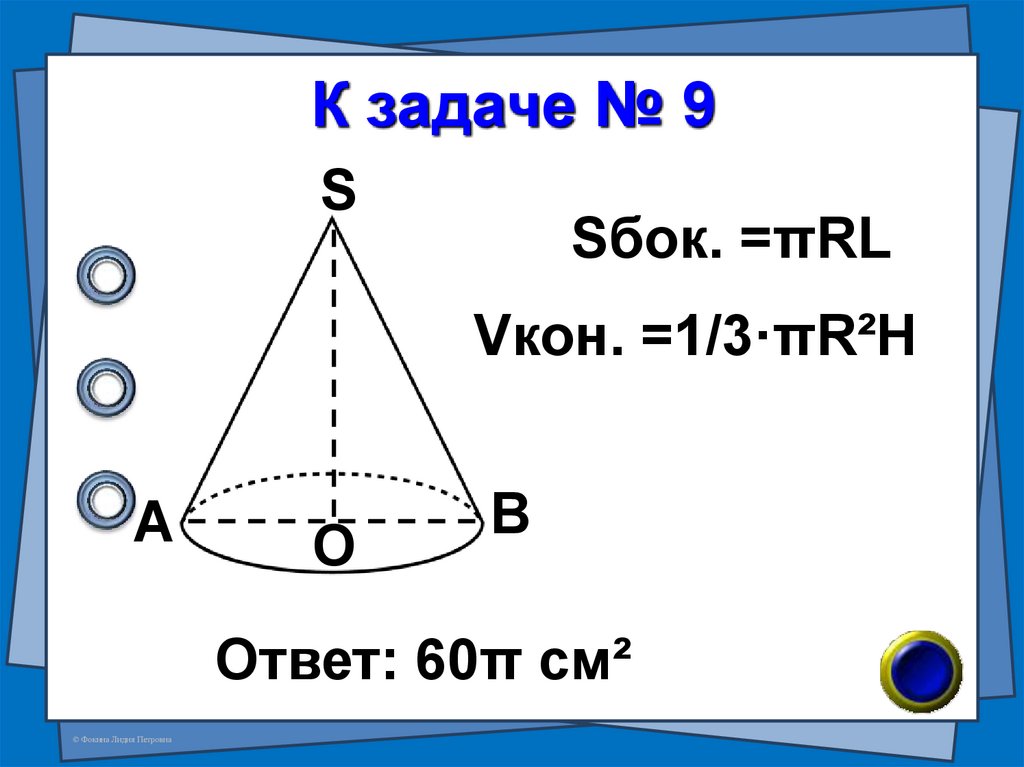
36. К задаче № 9

S
Sбок. =πRL
Vкон. =1/3·πR²H
А
О
В
Ответ: 60π см²
© Фокина Лидия Петровна

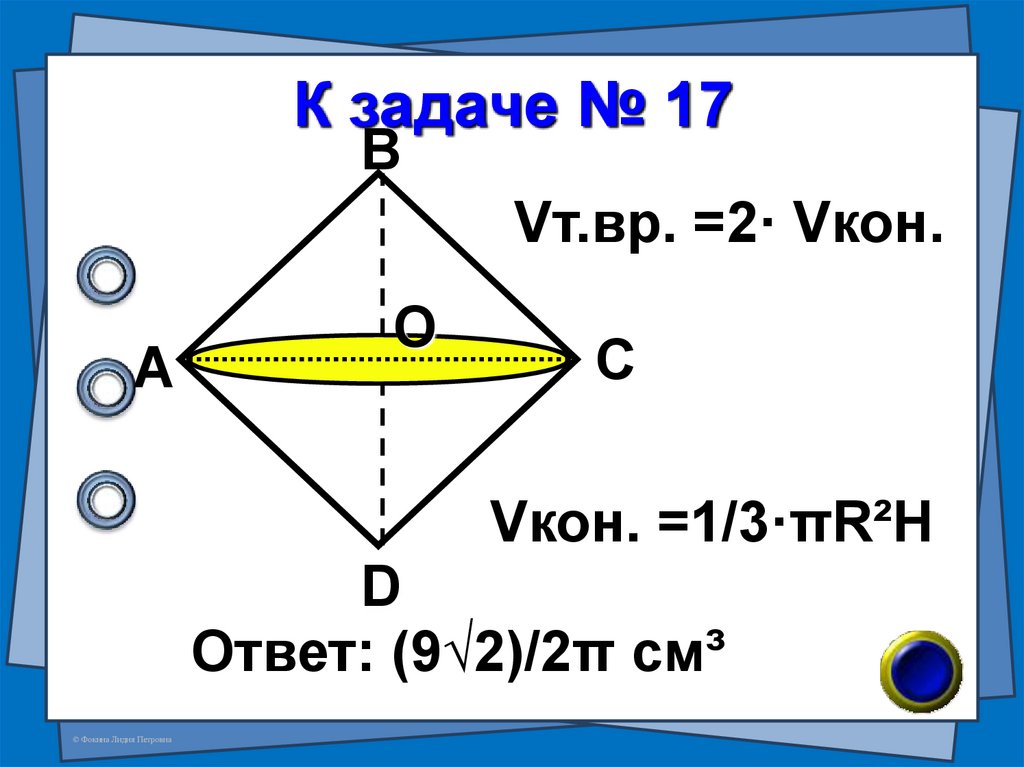
37. (В – 68 №7) Квадрат со стороной 3см вращается вокруг своей диагонали. Найдите объём тела вращения.

№ 17
(В – 68 №7)
Квадрат со стороной 3см
вращается вокруг своей
диагонали. Найдите
объём тела вращения.
© Фокина Лидия Петровна

38. К задаче № 17

В
Vт.вр. =2· Vкон.
А
О
С
Vкон. =1/3·πR²H
D
Ответ: (9√2)/2π см³
© Фокина Лидия Петровна

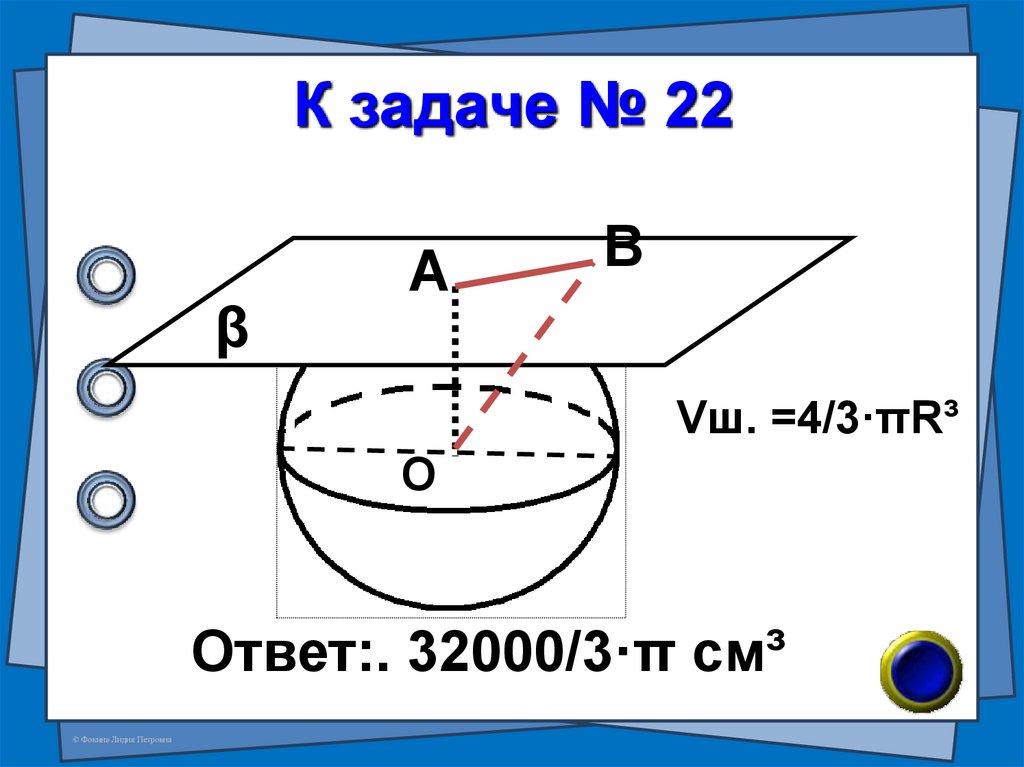
39. (В-84 №7) Шар с центром в точке О касается плоскости в точка А. Точка В лежит в плоскости касания. Найдите объём шара, если

№ 22
(В-84 №7)
Шар с центром в точке О
касается плоскости в точка А.
Точка В лежит в плоскости
касания. Найдите объём
шара, если АВ=21см,
ВО=29см.
© Фокина Лидия Петровна

40. К задаче № 22

β
А
В
Vш. =4/3·πR³
О
Ответ:. 32000/3·π см³
© Фокина Лидия Петровна

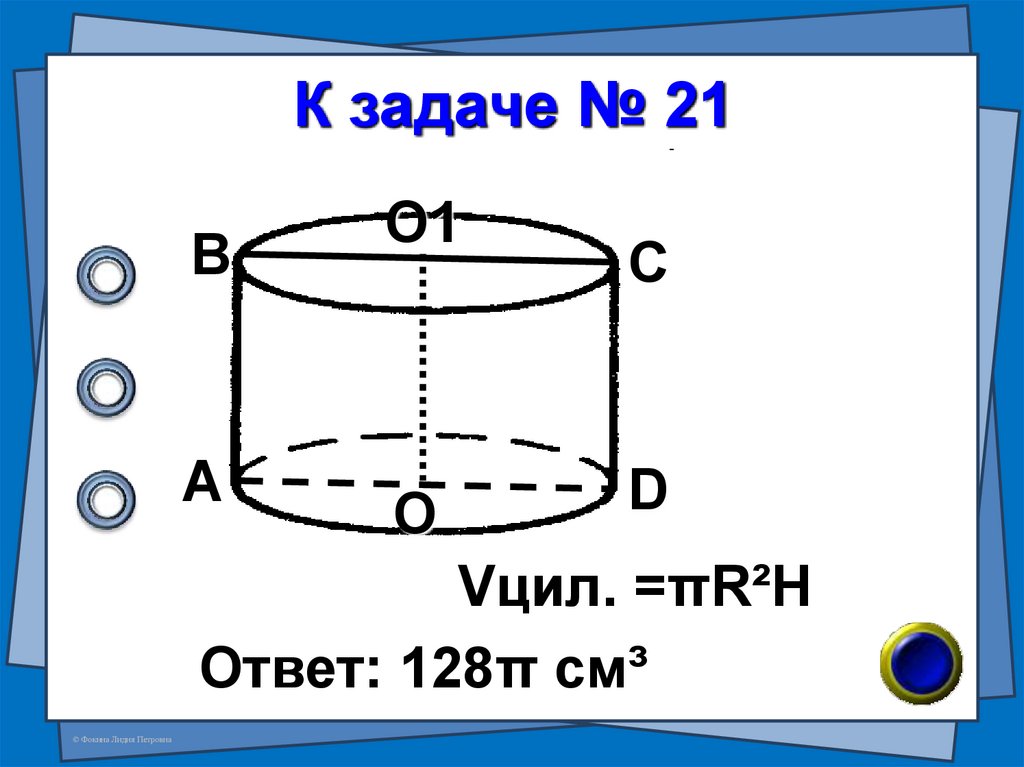
41. № 21 (В-82 №7)

Площадь осевого сечения
цилиндра равна 64см², а
его образующая равна
диаметру основания.
Найдите объём цилиндра.
© Фокина Лидия Петровна

42. К задаче № 21

В
А
О1
О
С
D
Vцил. =πR²H
Ответ: 128π см³
© Фокина Лидия Петровна

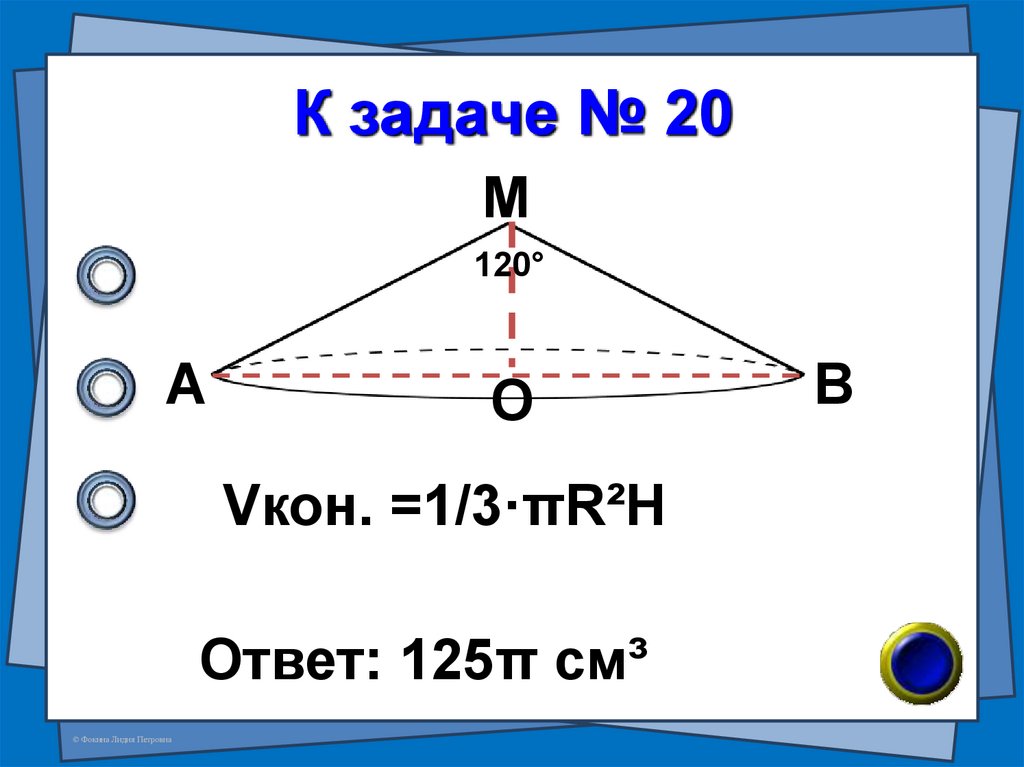
43. № 20 (В-78 №7)

Высота конуса равна 5см, а
угол при вершине осевого
сечения равен 120°.
Найдите объём конуса.
© Фокина Лидия Петровна

44. К задаче № 20

М
120°
А
О
Vкон. =1/3·πR²H
Ответ: 125π см³
© Фокина Лидия Петровна
В

45. № 19 (В-70 №7)

Найдите объём тела,
полученного при вращении
квадрата со стороной 7см
вокруг прямой, соединяющей
середины противолежащих
сторон.
© Фокина Лидия Петровна

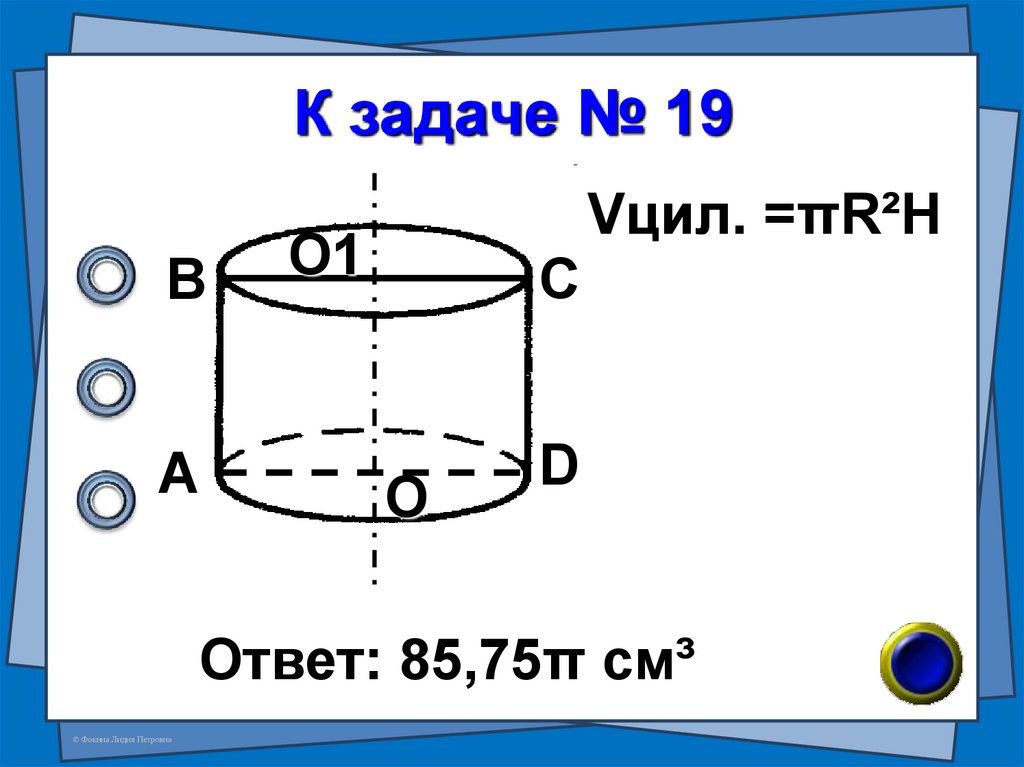
46. К задаче № 19

В
А
Vцил. =πR²H
О1
С
О
D
Ответ: 85,75π см³
© Фокина Лидия Петровна

47. № 18 (В-69 №7)

Найдите объём тела,
полученного при вращении
прямоугольника со
сторонами 6см и 8см вокруг
прямой, которая проходит
через середины его меньших
сторон.
© Фокина Лидия Петровна

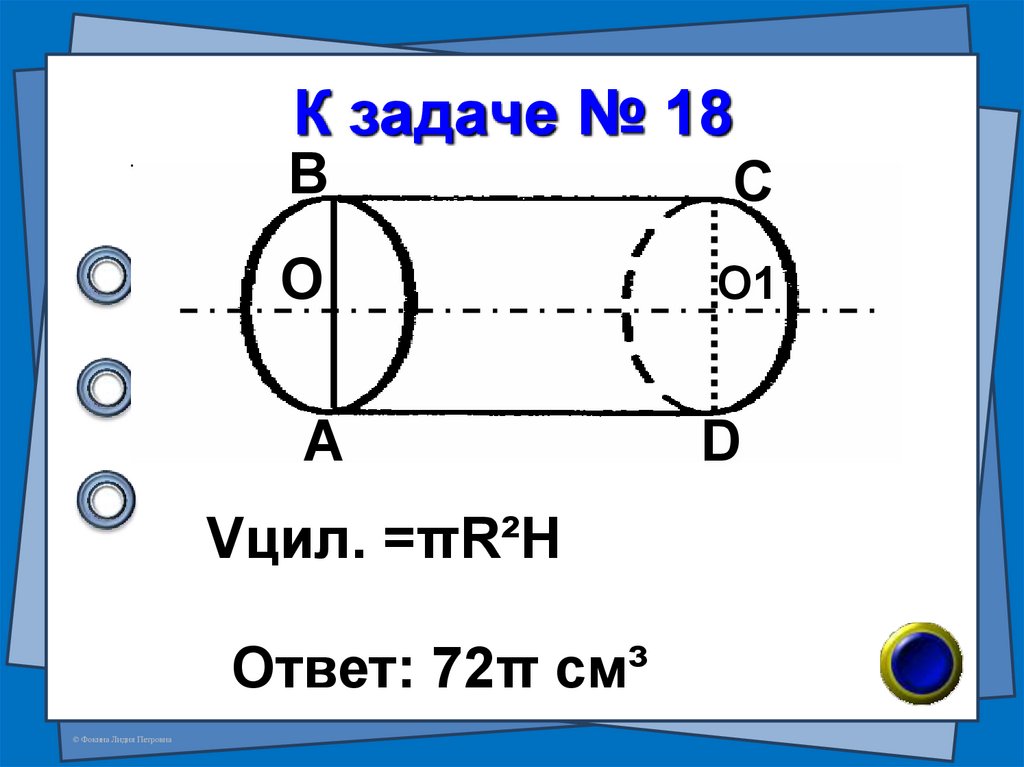
48. К задаче № 18

В
С
О
О1
А
D
Vцил. =πR²H
Ответ: 72π см³
© Фокина Лидия Петровна

49. (В-85 №7) Полукруг свернут в виде боковой поверхности конуса. Радиус основания конуса 5см. Найдите объём конуса.

№ 23
(В-85 №7)
Полукруг свернут в виде
боковой поверхности
конуса. Радиус основания
конуса 5см. Найдите
объём конуса.
© Фокина Лидия Петровна

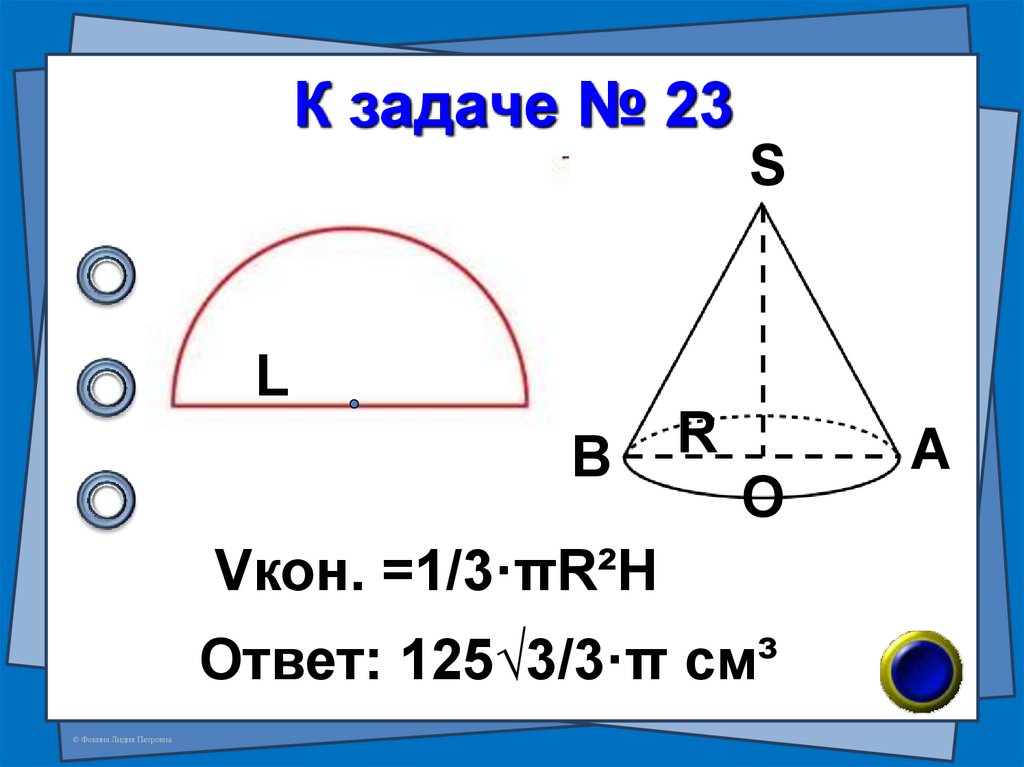
50. К задаче № 23

S
L
В
R
О
Vкон. =1/3·πR²H
Ответ: 125√3/3·π см³
© Фокина Лидия Петровна
А

51. (В-88 №7) Ромб со стороной 5см и углом 60° вращается вокруг своей меньшей диагонали. Определите объём тела вращения.

№ 24
(В-88 №7)
Ромб со стороной 5см и
углом 60° вращается
вокруг своей меньшей
диагонали. Определите
объём тела вращения.
© Фокина Лидия Петровна

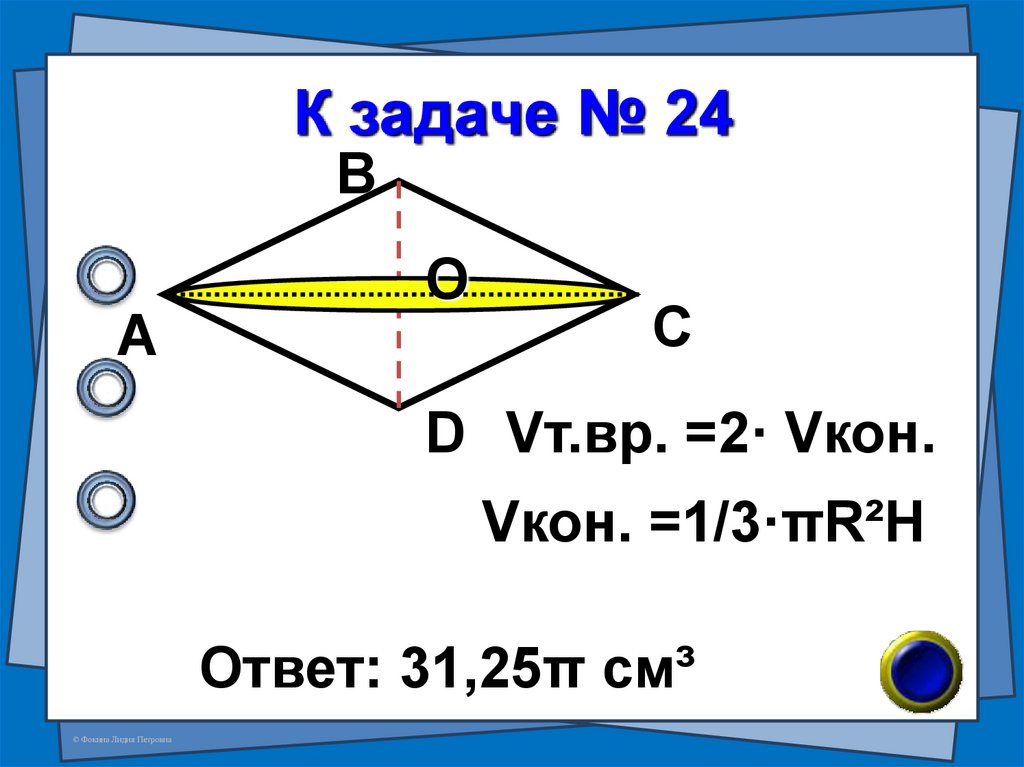
52. К задаче № 24

В
А
О
С
D Vт.вр. =2· Vкон.
Vкон. =1/3·πR²H
Ответ: 31,25π см³
© Фокина Лидия Петровна

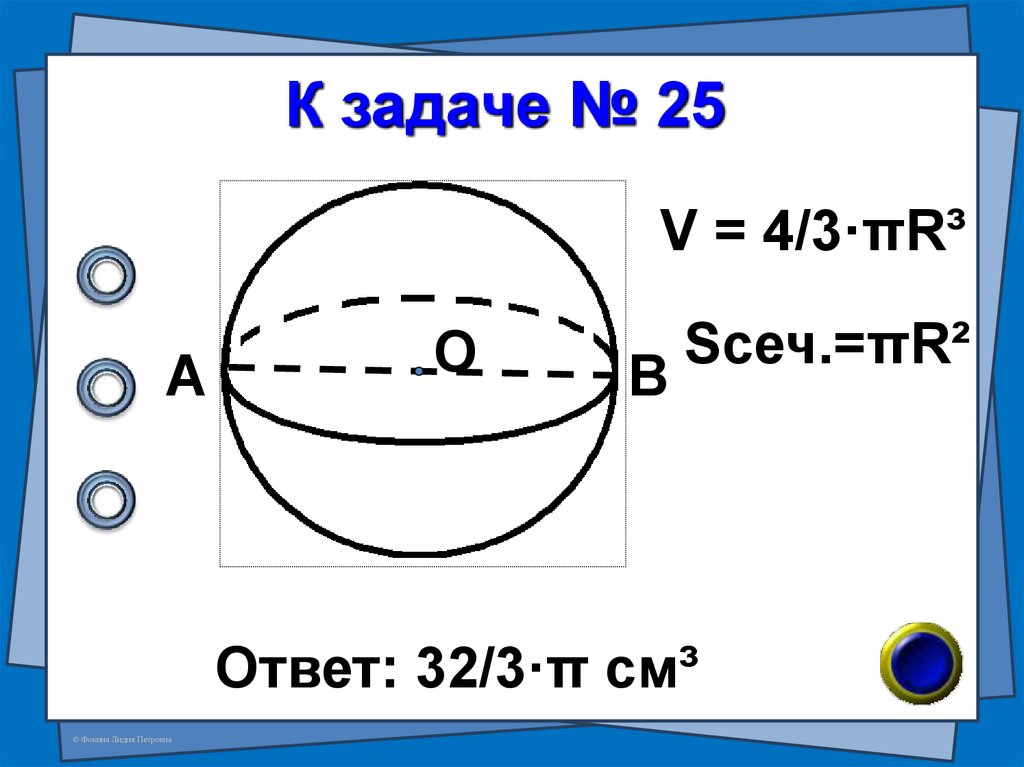
53. № 25 (В-89 №7)

Площадь сечения шара
плоскостью, проходящей
через его центр, равна
4π см². Найдите объём
шара.
© Фокина Лидия Петровна

54. К задаче № 25

V = 4/3·πR³
А
О
В
Sсеч.=πR²
Ответ: 32/3·π см³
© Фокина Лидия Петровна

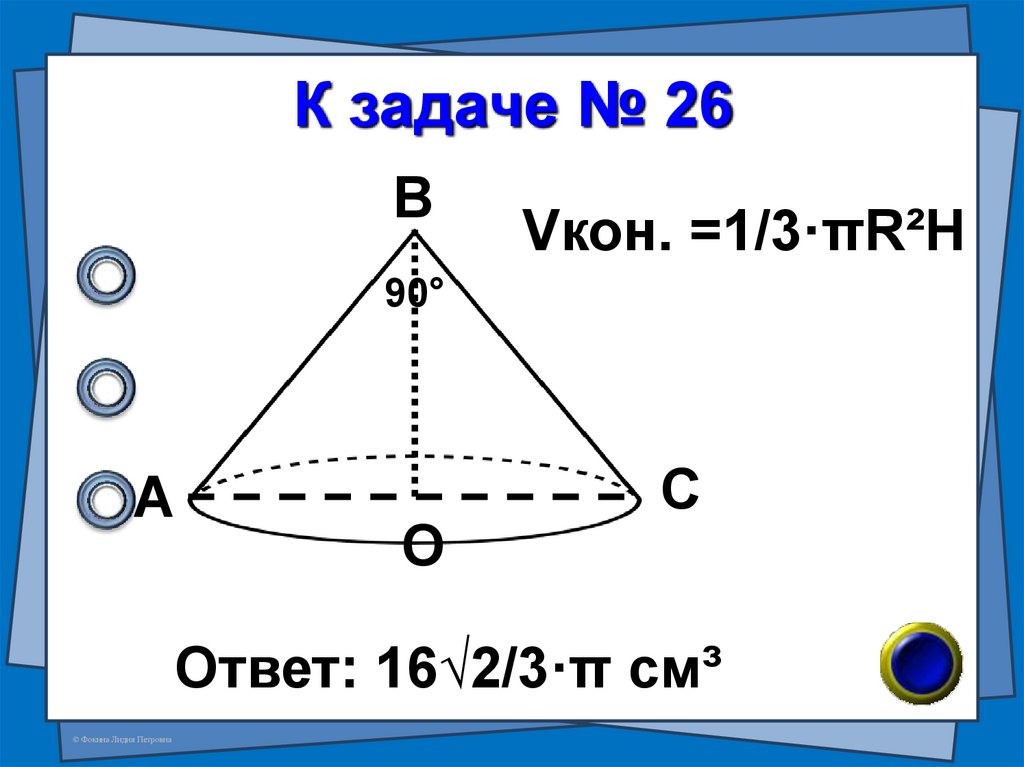
55. № 26 (В-91 №7)

Образующая конуса равна
4см, а угол при вершине
осевого сечения равен 90°.
Найдите объём конуса.
© Фокина Лидия Петровна

56. К задаче № 26

В
Vкон. =1/3·πR²H
90°
А
О
С
Ответ: 16√2/3·π см³
© Фокина Лидия Петровна

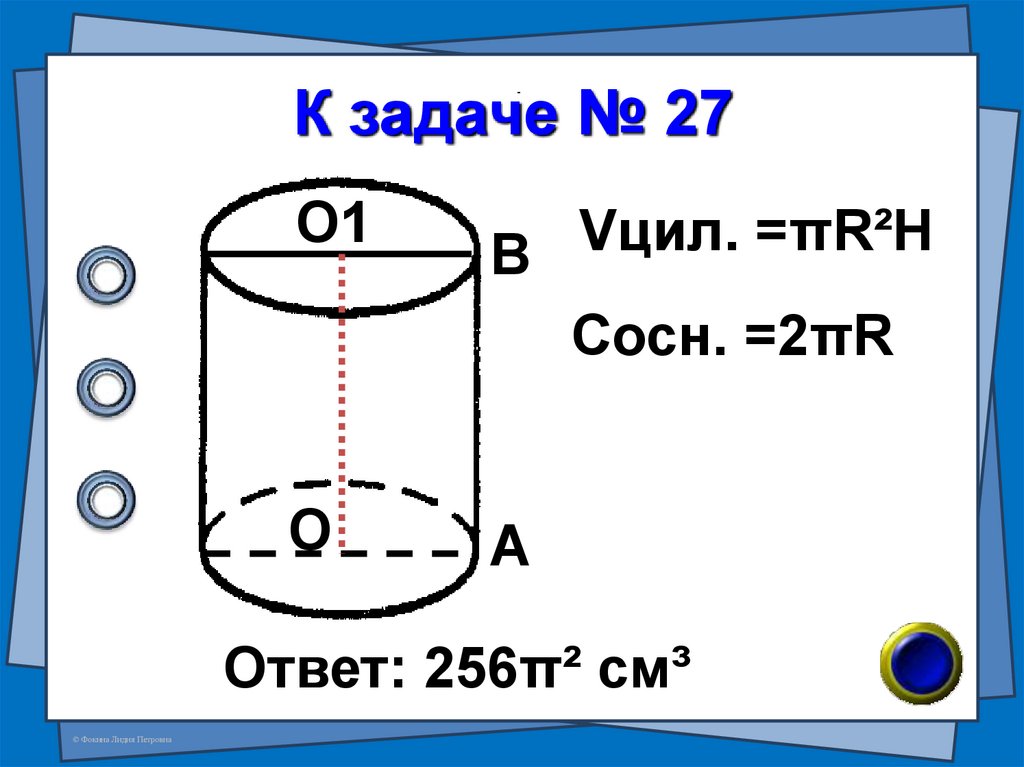
57. № 27 (в-96 №7)

Радиус основания цилиндра
равен 4см, высота в два
раза больше длины
окружности основания.
Найдите объём цилиндра.
© Фокина Лидия Петровна

58. К задаче № 27

О1
Vцил.
=πR²H
В
Сосн. =2πR
О
А
Ответ: 256π² см³
© Фокина Лидия Петровна