Тела вращения

1. ТЕЛА ВРАЩЕНИЯ

ПОУ. Геометрия. 11 класс

2.

1.
2.
3.
4.
5.
ФИО
Место работы
Должность
Предмет
Класс
Терентьева Татьяна Авенировна
МБОУ СОШ № 62 г. Архангельск
Учитель
Математика
11
6. Цель урока: систематизация и обобщение знаний по теме
«Тела вращения».
7. Задачи:
а) повторить понятия цилиндра, конуса и сферы, их элементов;
б) повторить формулы площади поверхностей и объемов тел
вращения;
в) закрепить способы решения задач на тела вращения.
8. Формы работы учащихся:
Фронтальная, самостоятельная работа, индивидуальная работа,
работа с презентацией
9. Необходимое техническое оборудование: компьютер; проектор;
экран
10. Структура и ход урока

3. План урока

ПЛАН УРОКА
Д/з:
Прототипы В13
(открытый банк заданий)
№ 1 – 20 из 60
(письменно и обязательно).
mathege.ru

4. План урока

ПЛАН УРОКА
1.Повторение теории
2.Решение задач
3.Тест
4.Самостоятельная работа
5.Подведение итогов

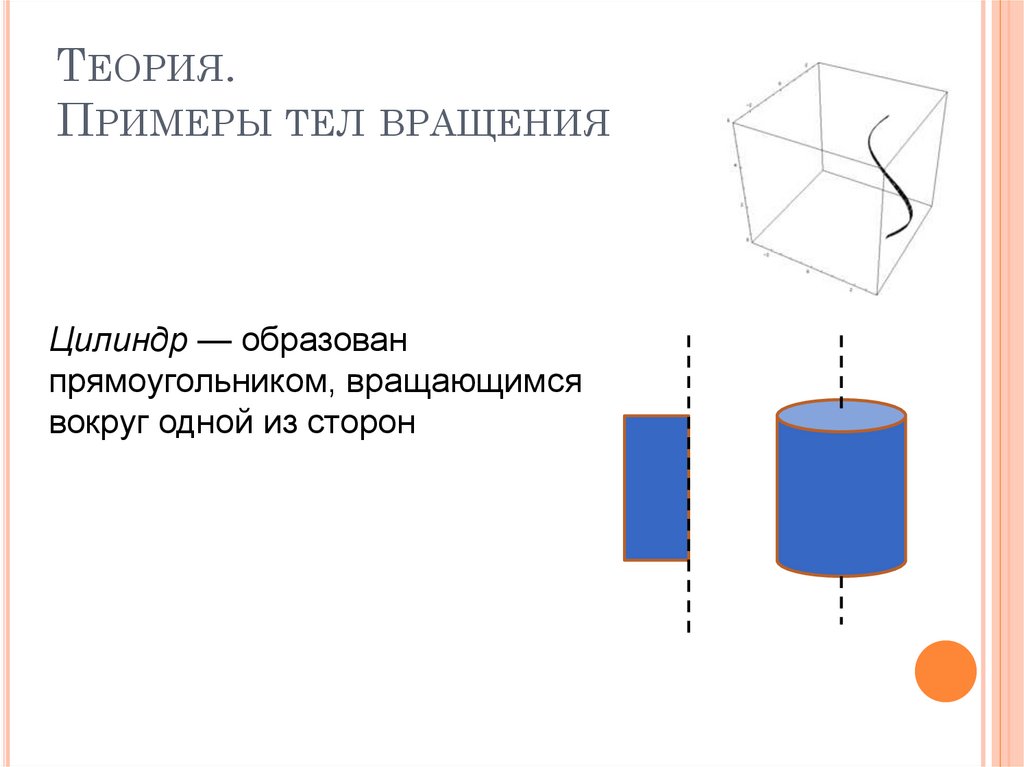
5. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Цилиндр — образован
прямоугольником, вращающимся
вокруг одной из сторон

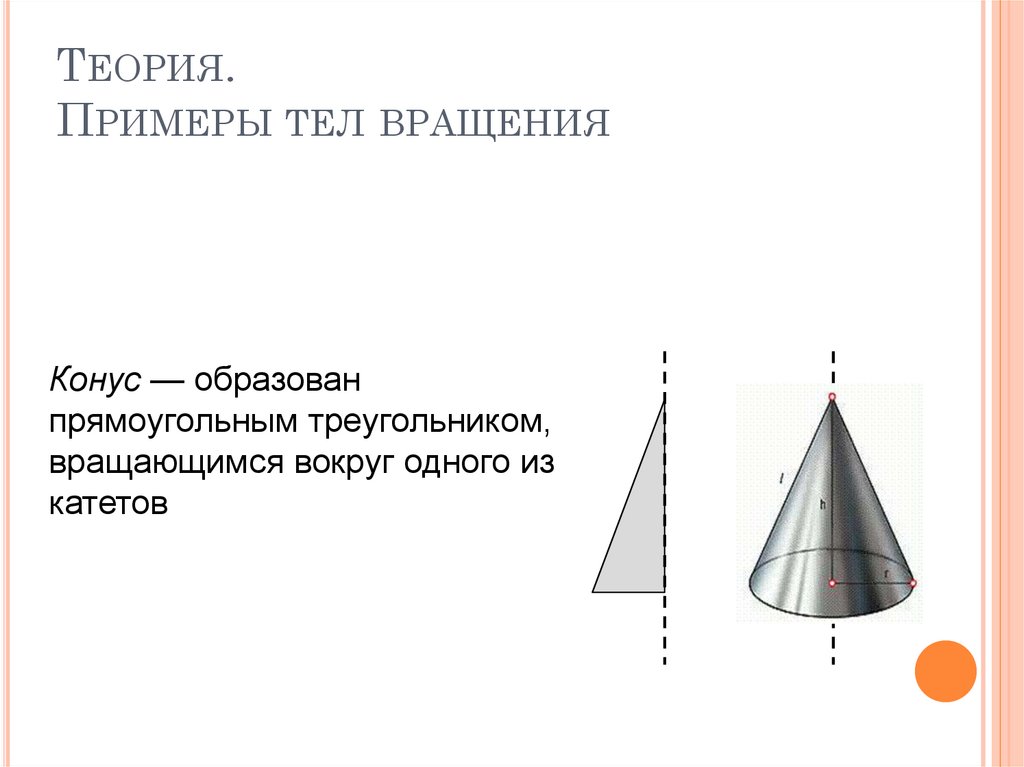
6. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Конус — образован
прямоугольным треугольником,
вращающимся вокруг одного из
катетов

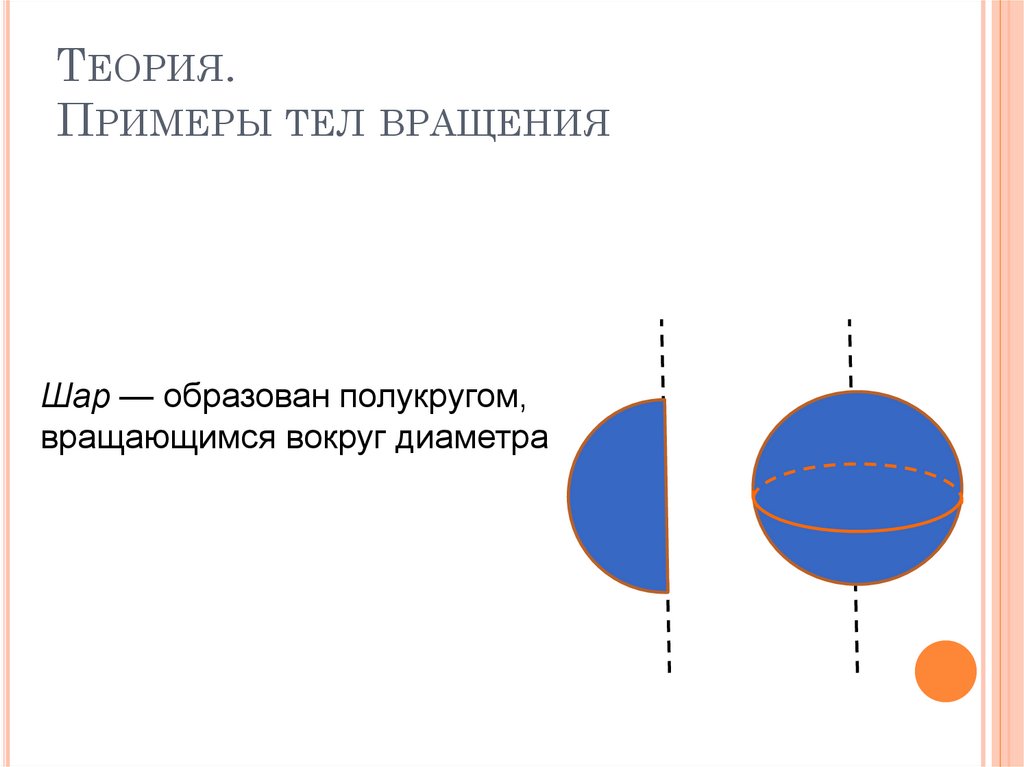
7. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Шар — образован полукругом,
вращающимся вокруг диаметра

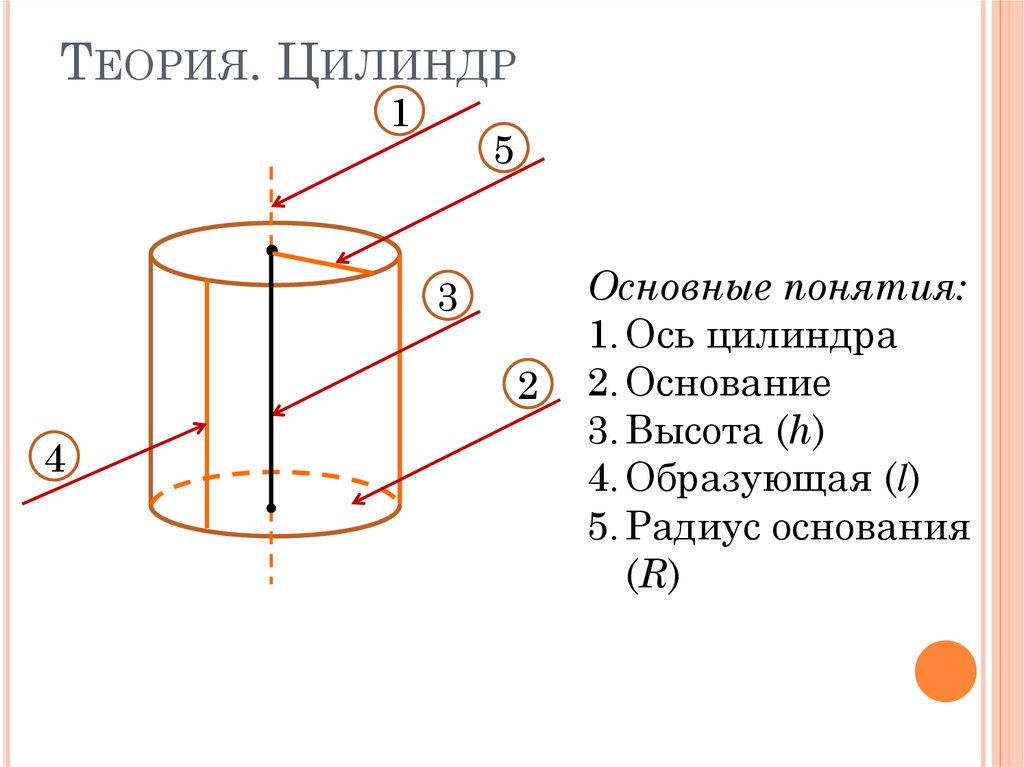
8. Теория. Цилиндр

ТЕОРИЯ. ЦИЛИНДР
1
.
5
3
2
4
.
Основные понятия:
1. Ось цилиндра
2. Основание
3. Высота (h)
4. Образующая (l)
5. Радиус основания
(R)

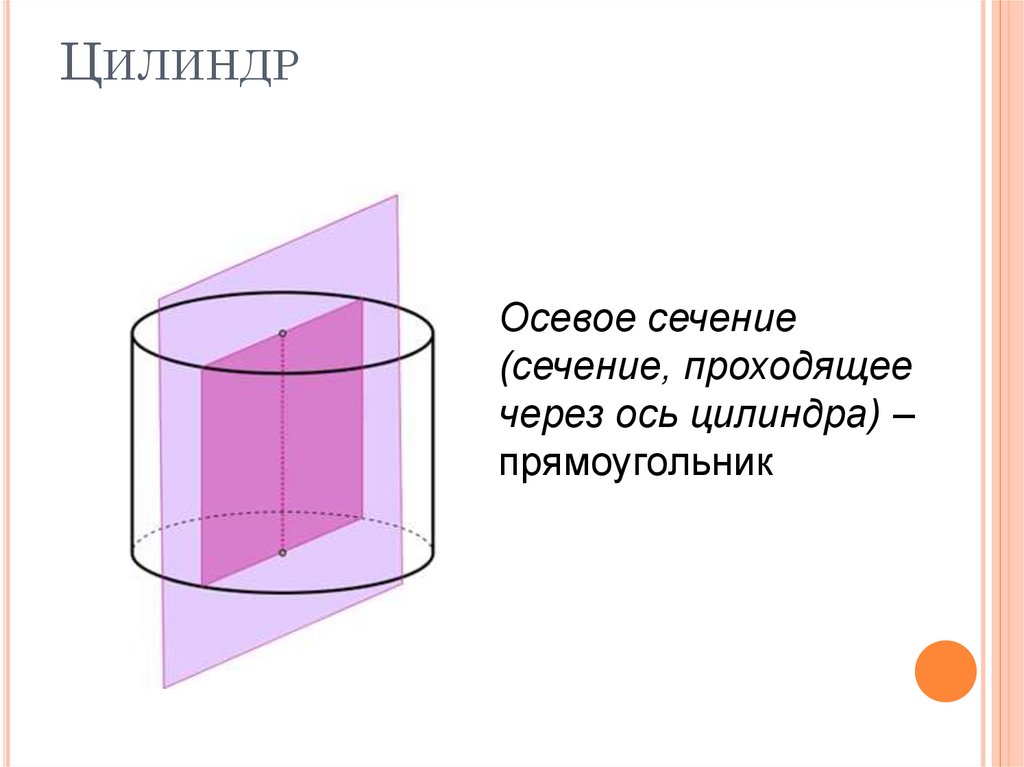
9. Цилиндр

ЦИЛИНДР
Осевое сечение
(сечение, проходящее
через ось цилиндра) –
прямоугольник

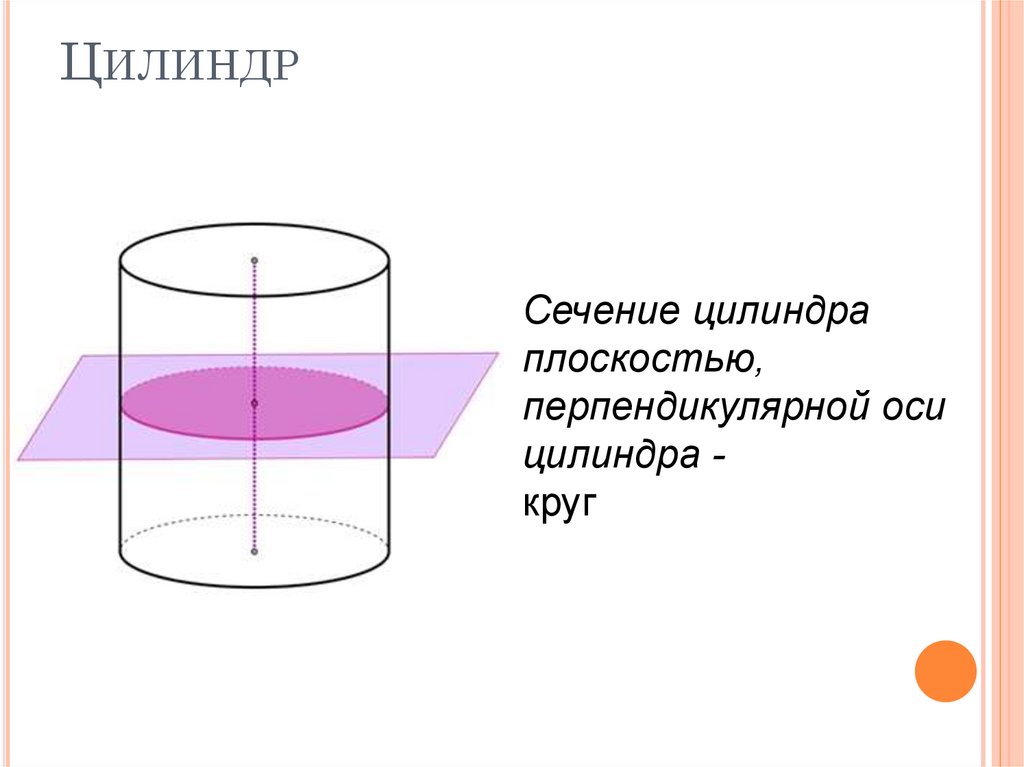
10. Цилиндр

ЦИЛИНДР
Сечение цилиндра
плоскостью,
перпендикулярной оси
цилиндра круг

11. Цилиндр

ЦИЛИНДР
Формулы:
S осн R
2
- площадь основания
S бок 2 Rh
- площадь боковой
поверхности
V R 2 h
- объем
R радиус; h высота

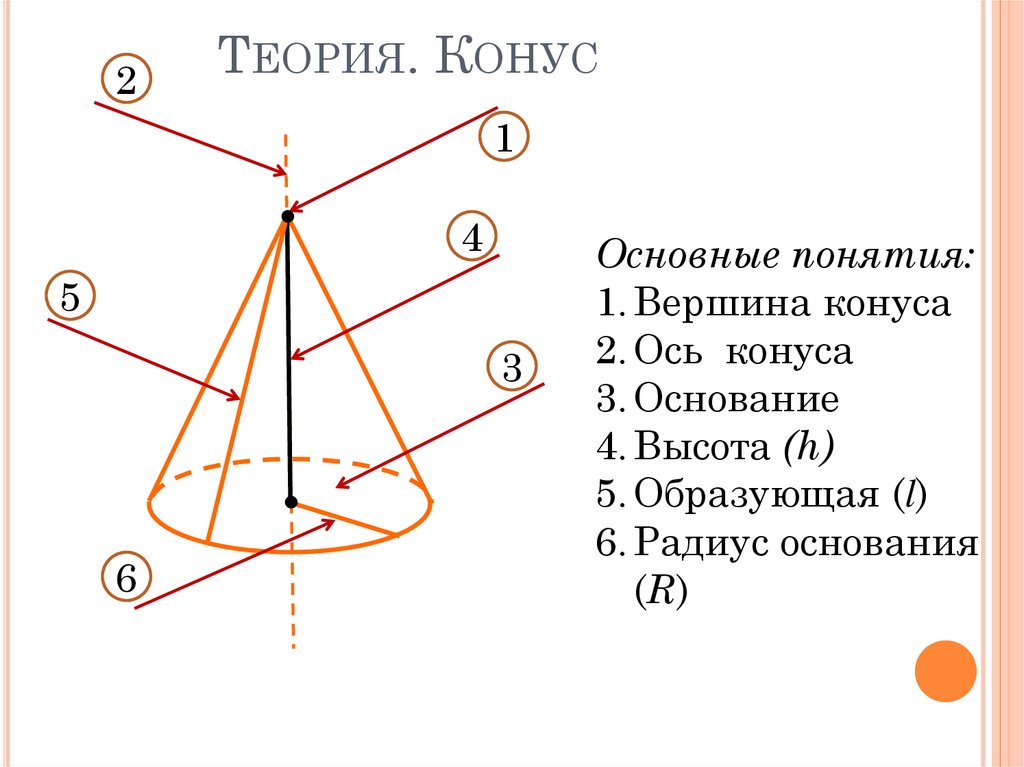
12. Теория. Конус

2
ТЕОРИЯ. КОНУС
.
1
4
5
3
.
6
Основные понятия:
1. Вершина конуса
2. Ось конуса
3. Основание
4. Высота (h)
5. Образующая (l)
6. Радиус основания
(R)

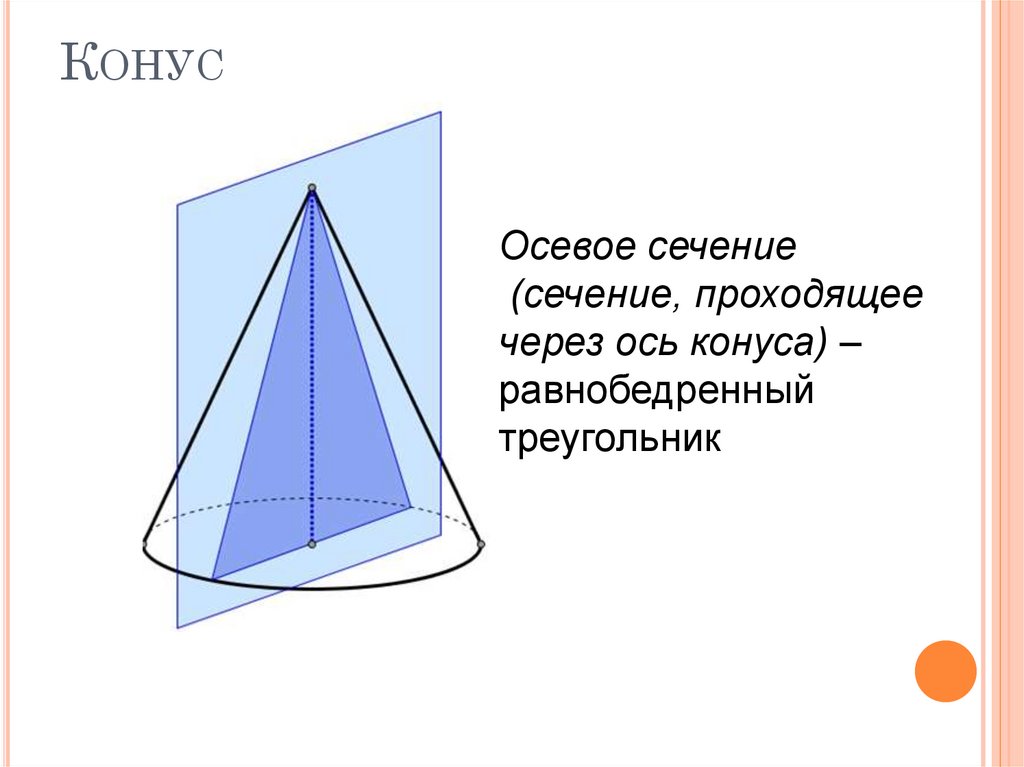
13. Конус

КОНУС
Осевое сечение
(сечение, проходящее
через ось конуса) –
равнобедренный
треугольник

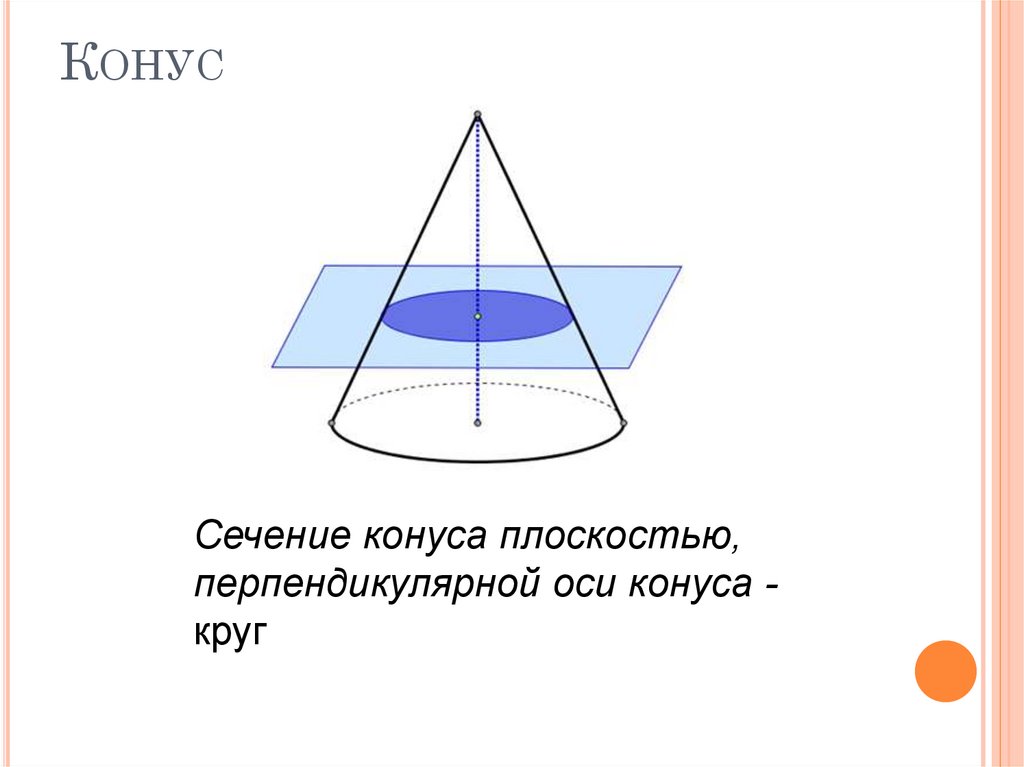
14. Конус

КОНУС
Сечение конуса плоскостью,
перпендикулярной оси конуса круг

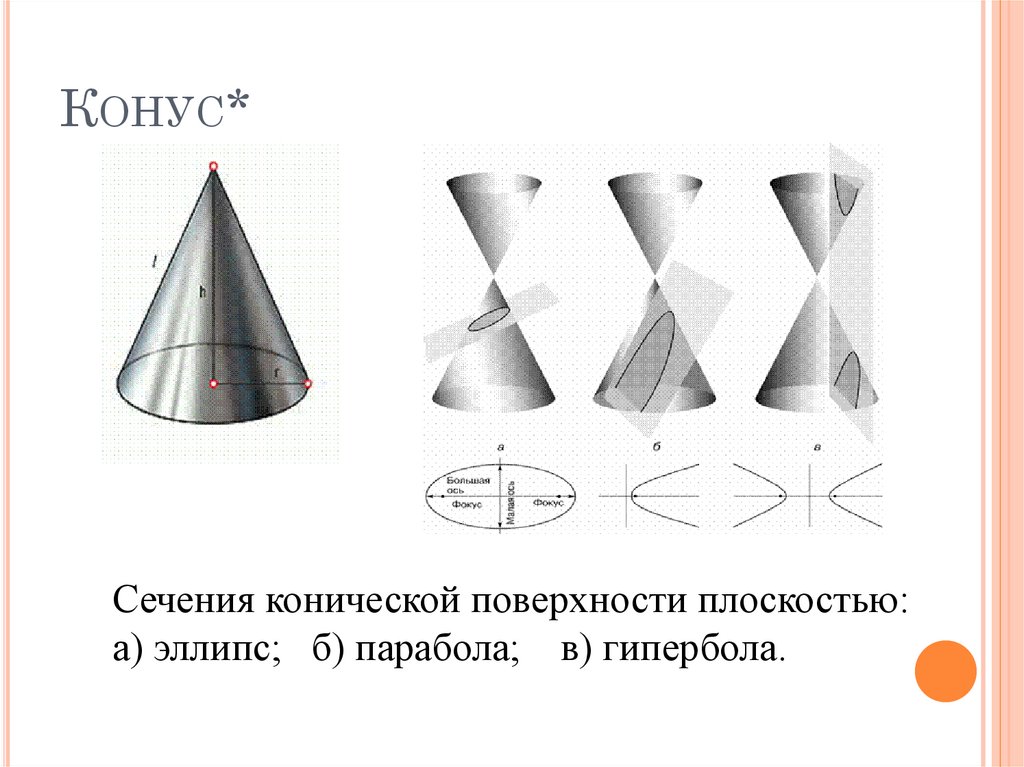
15. Конус*

КОНУС*
Сечения конической поверхности плоскостью:
а) эллипс; б) парабола; в) гипербола.

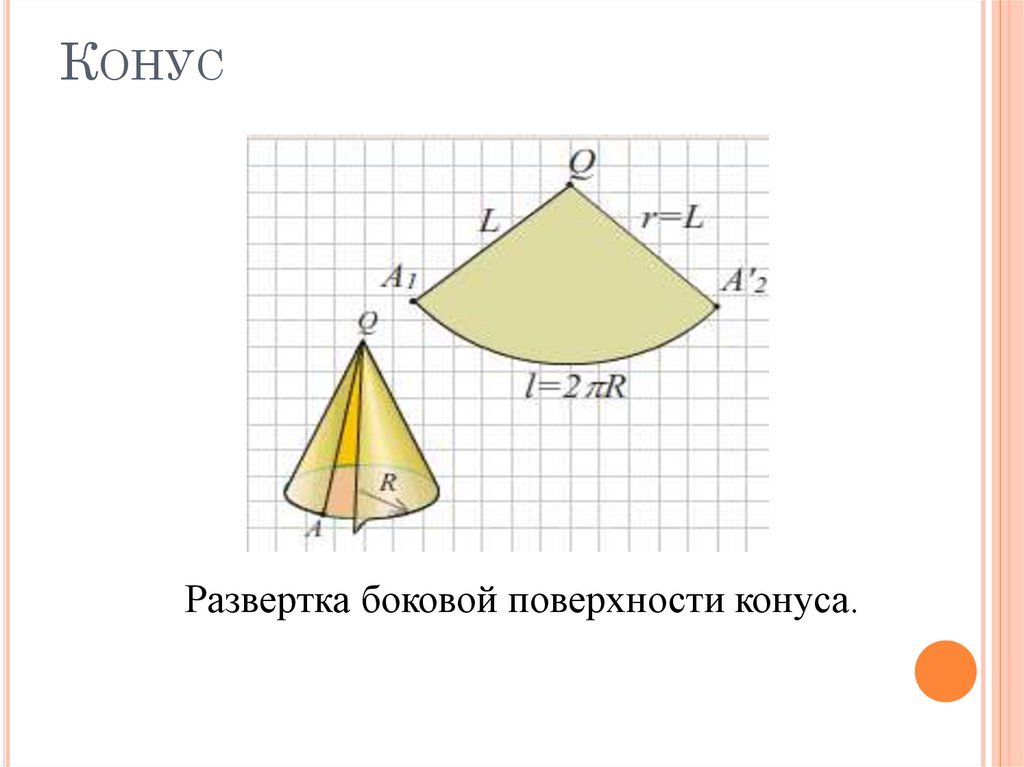
16. Конус

КОНУС
Развертка боковой поверхности конуса.

17. Конус

КОНУС
Формулы:
S осн R
2
- площадь основания
Sбок Rl
- площадь боковой
поверхности
1 2
V R h
3
- объем
R радиус; h высота; l образующая

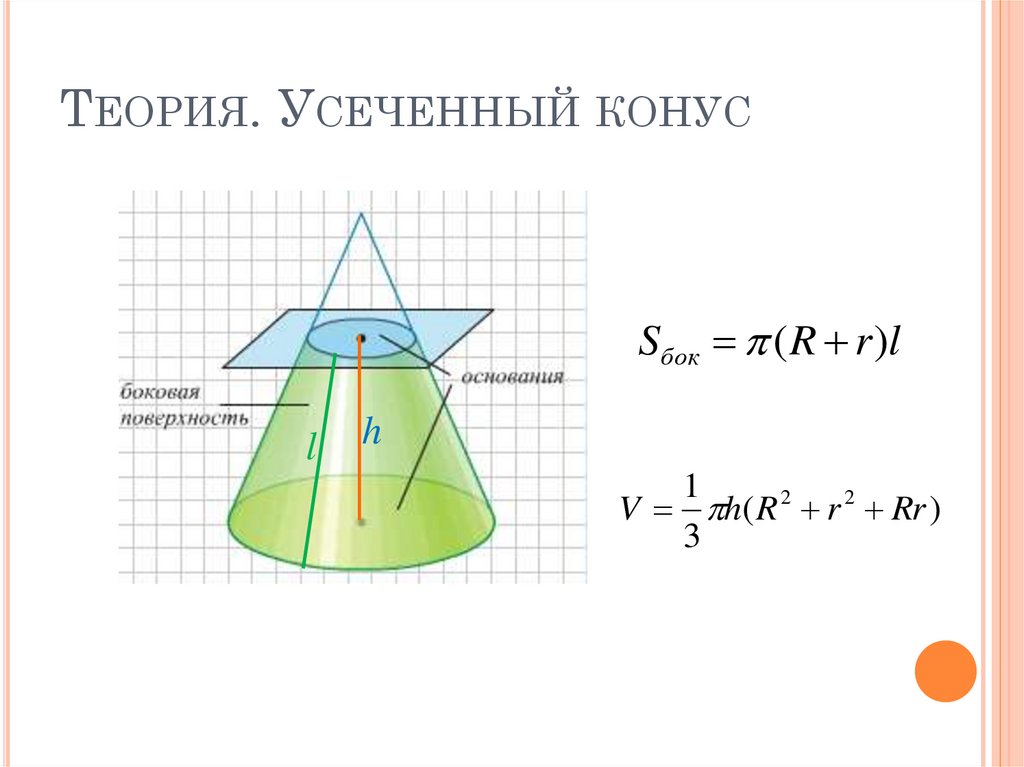
18. Теория. Усеченный конус

ТЕОРИЯ. УСЕЧЕННЫЙ КОНУС
Sбок ( R r )l
l
h
1
V h( R 2 r 2 Rr )
3

19. Теория. Сфера и шар

ТЕОРИЯ. СФЕРА И ШАР
т.О – центр
сферы
R - радиус
Площадь поверхности:
S 4 R 2
Объём:
4 3
V R
3

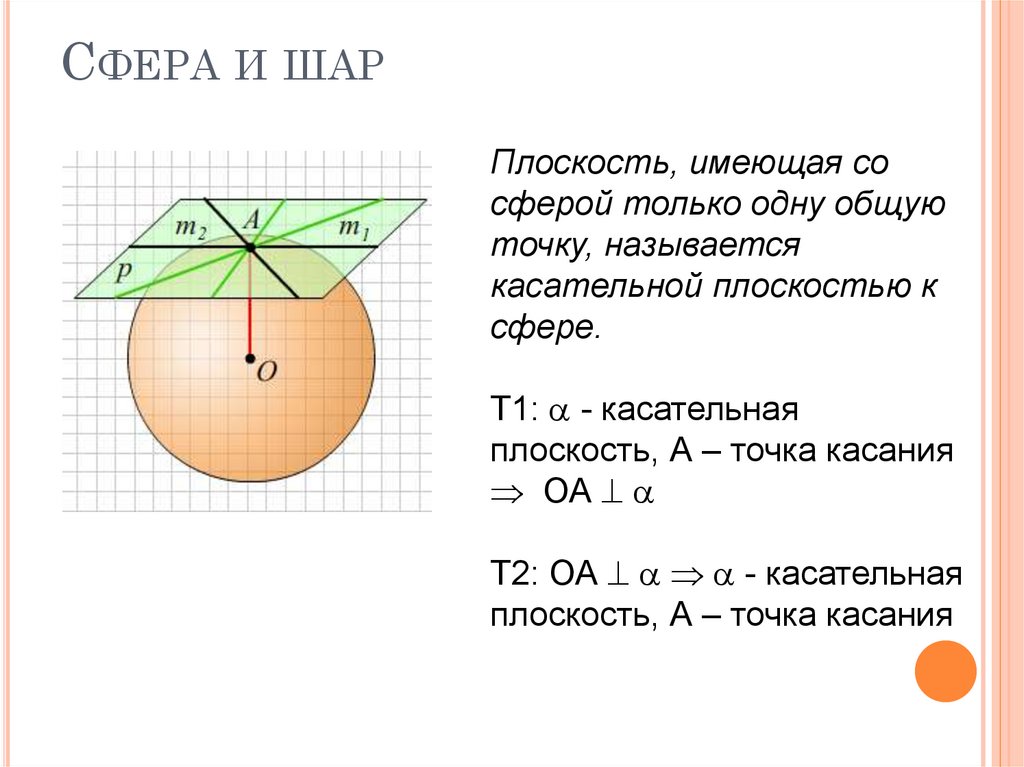
20. Сфера и шар

СФЕРА И ШАР
Плоскость, имеющая со
сферой только одну общую
точку, называется
касательной плоскостью к
сфере.
Т1: - касательная
плоскость, А – точка касания
ОА
Т2: ОА - касательная
плоскость, А – точка касания

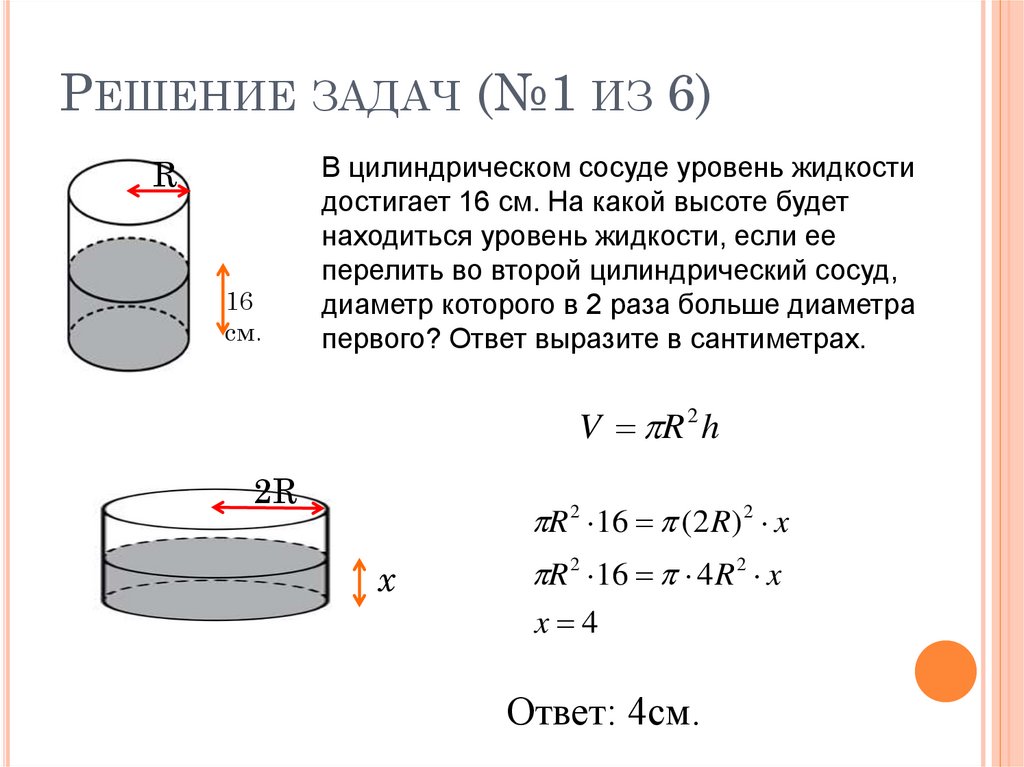
21. Решение задач (№1 из 6)

РЕШЕНИЕ ЗАДАЧ (№1 ИЗ 6)
R
16
см.
В цилиндрическом сосуде уровень жидкости
достигает 16 см. На какой высоте будет
находиться уровень жидкости, если ее
перелить во второй цилиндрический сосуд,
диаметр которого в 2 раза больше диаметра
первого? Ответ выразите в сантиметрах.
V R 2 h
2R
R 2 16 (2 R) 2 x
x
R 2 16 4 R 2 x
x 4
Ответ: 4см.

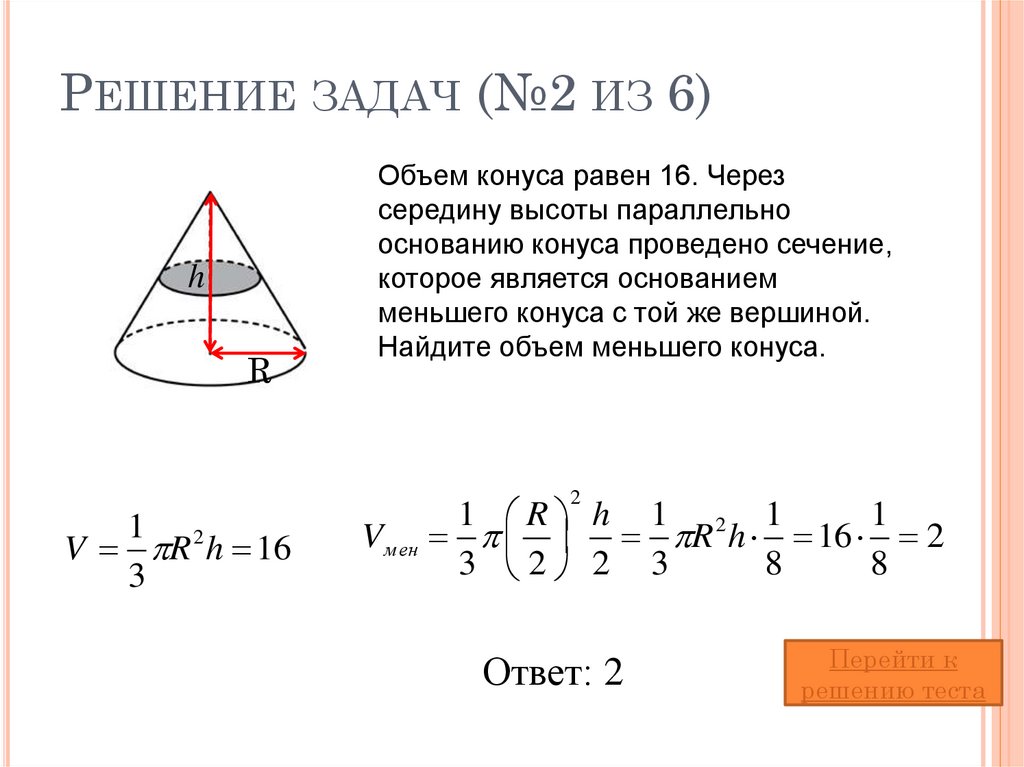
22. Решение задач (№2 из 6)

РЕШЕНИЕ ЗАДАЧ (№2 ИЗ 6)
h
R
Объем конуса равен 16. Через
середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием
меньшего конуса с той же вершиной.
Найдите объем меньшего конуса.
2
1 2
V R h 16
3
1 R h 1 2 1
1
Vм ен R h 16 2
3 2 2 3
8
8
Ответ: 2
Перейти к
решению теста

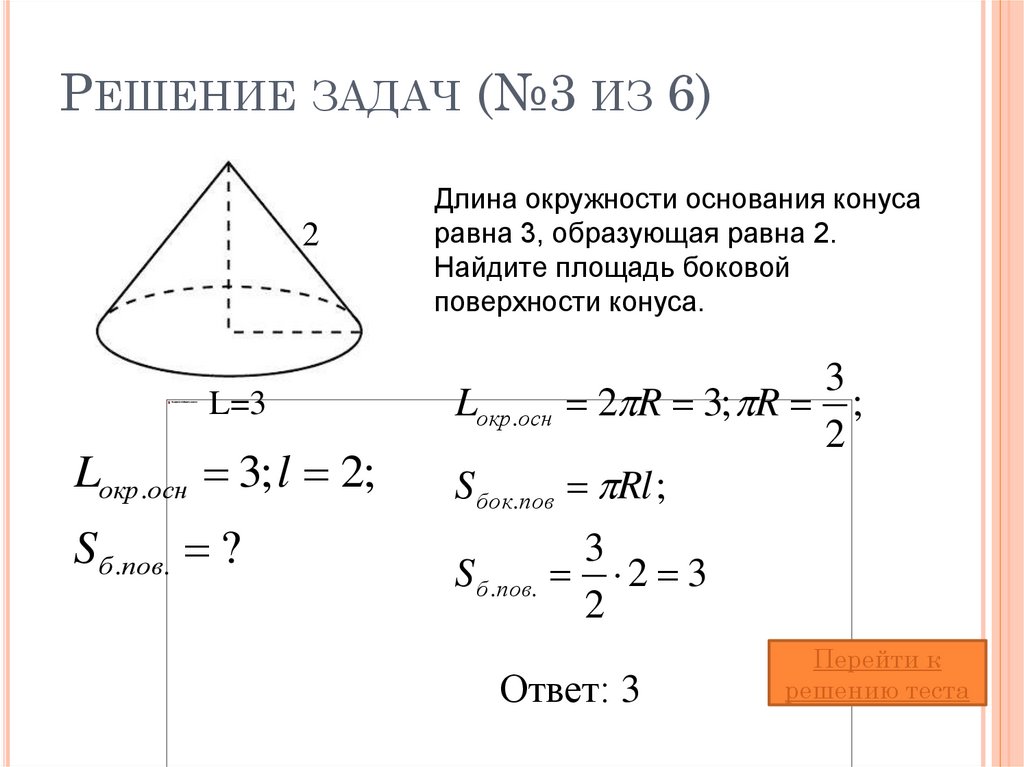
23. Решение задач (№3 из 6)

РЕШЕНИЕ ЗАДАЧ (№3 ИЗ 6)
2
L=3
Lокр.осн 3; l 2;
S б .пов. ?
Длина окружности основания конуса
равна 3, образующая равна 2.
Найдите площадь боковой
поверхности конуса.
3
Lокр.осн 2 R 3; R ;
2
S бок.пов Rl ;
S б .пов.
3
2 3
2
Ответ: 3
Перейти к
решению теста

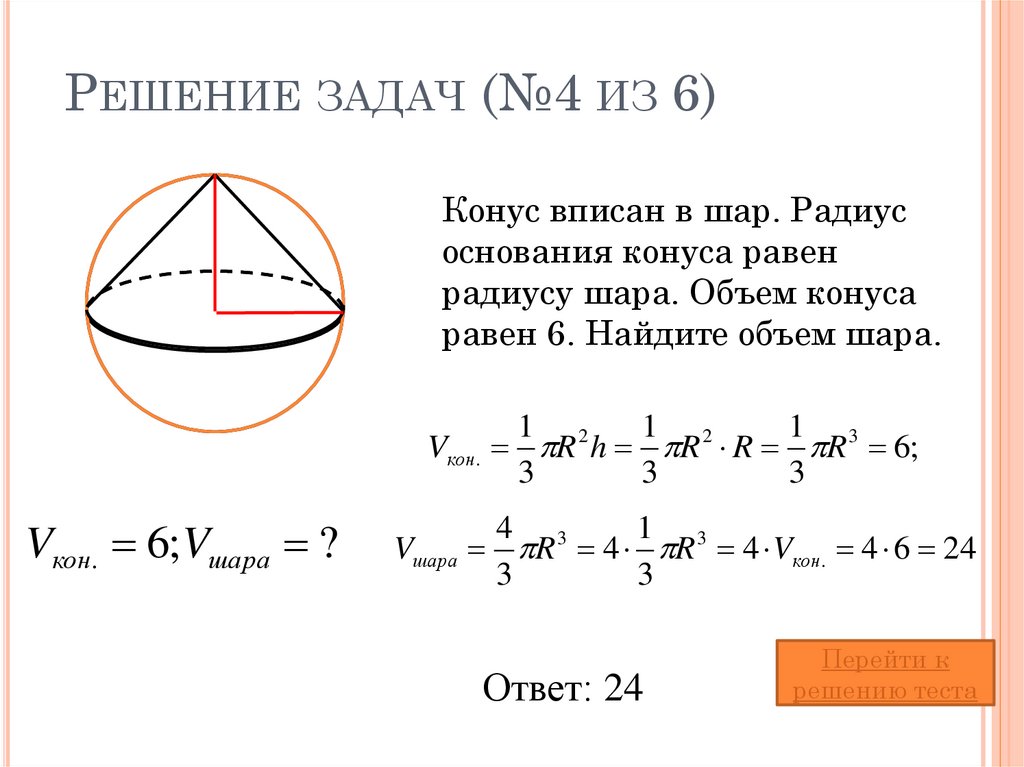
24. Решение задач (№4 из 6)

РЕШЕНИЕ ЗАДАЧ (№4 ИЗ 6)
Конус вписан в шар. Радиус
основания конуса равен
радиусу шара. Объем конуса
равен 6. Найдите объем шара.
Vкон.
Vкон. 6;Vшара ?
Vшара
1 2
1 2
1 3
R h R R R 6;
3
3
3
4 3
1 3
R 4 R 4 Vкон. 4 6 24
3
3
Ответ: 24
Перейти к
решению теста

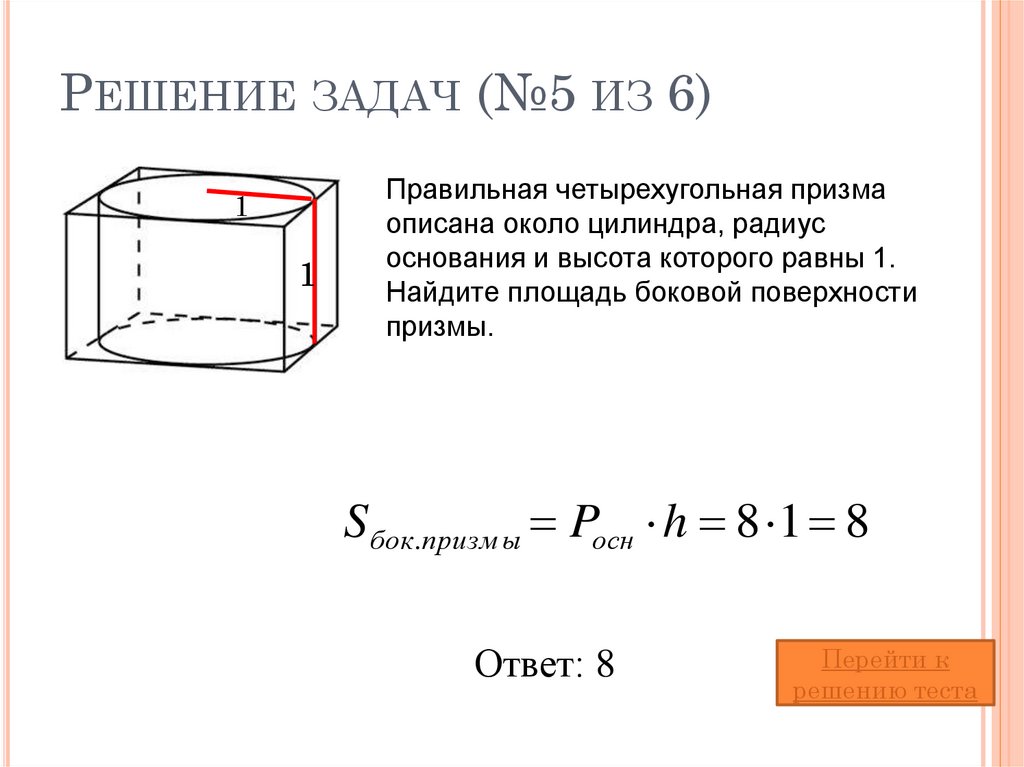
25. Решение задач (№5 из 6)

РЕШЕНИЕ ЗАДАЧ (№5 ИЗ 6)
1
1
Правильная четырехугольная призма
описана около цилиндра, радиус
основания и высота которого равны 1.
Найдите площадь боковой поверхности
призмы.
S бок.призм ы Pосн h 8 1 8
Ответ: 8
Перейти к
решению теста

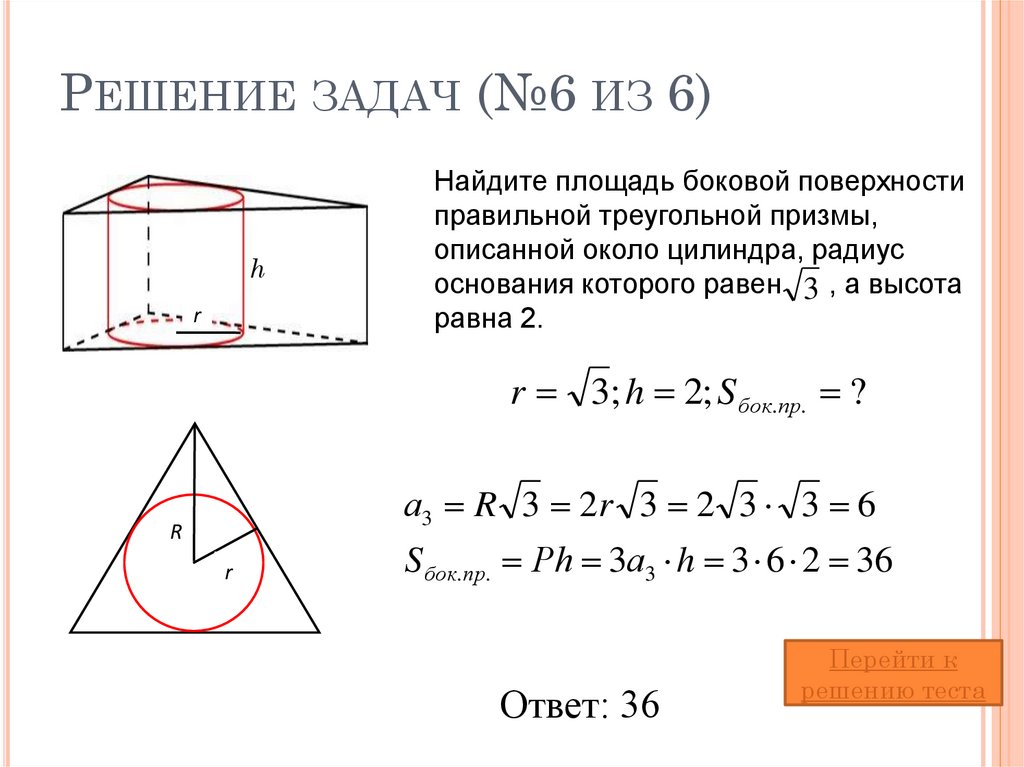
26. Решение задач (№6 из 6)

РЕШЕНИЕ ЗАДАЧ (№6 ИЗ 6)
h
r
Найдите площадь боковой поверхности
правильной треугольной призмы,
описанной около цилиндра, радиус
основания которого равен 3 , а высота
равна 2.
r 3; h 2; S бок.пр. ?
а3 R 3 2r 3 2 3 3 6
R
rr
S бок.пр. Рh 3а3 h 3 6 2 36
Ответ: 36
Перейти к
решению теста

27. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
а) его высота увеличится в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

28. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
б) его радиус увеличится в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

29. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
в) его высота и радиус увеличатся
в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

30. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
а) его высота увеличится в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

31. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
б) диаметр основания увеличится
в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

32. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
в) его радиус увеличится в 2 раза,
а высота уменьшится в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

33. Тест

ТЕСТ
3. Диаметр шара увеличился в 2 раза.
а) Во сколько раз увеличился его объем
в 2 раза
в 4 раза
в 8 раз
в 16 раз

34. Тест

ТЕСТ
3. Диаметр шара увеличился в 2 раза.
б) Во сколько раз увеличилась площадь
его поверхности
в 2 раза
в 4 раза
в 8 раз
в 16 раз

35. Самостоятельная работа

САМОСТОЯТЕЛЬНАЯ РАБОТА
1. Радиус основания цилиндра равен 2, высота
равна 3. Найдите площадь боковой
поверхности цилиндра, деленную на .
2. Площадь большого круга шара равна 3.
Найдите площадь поверхности шара.
3.
Площадь боковой поверхности конуса в два
раза больше площади основания. Найдите
угол между образующей конуса и плоскостью
основания. Ответ дайте в градусах.
Дополнительны
е задачи
Перейти к
проверке

36. Самостоятельная работа (задача 1)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
1)
Радиус основания цилиндра
равен 2, высота равна 3. Найдите
площадь боковой поверхности
цилиндра, деленную на .
R 2; h 3;
S бок
?
S бок 2 Rh 2 2 3 12 ;
S бок
12
12
Ответ: 12

37. Самостоятельная работа (задача 2)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
2)
Площадь большого круга шара
равна 3. Найдите площадь
поверхности шара.
S круга 3;
S кр R 2 3;
S пов.шара ?
S пов.шара 4 R 2 4 3 12
Ответ: 12

38. Самостоятельная работа (задача 3)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
3)
A
C
B
S бок
2; ABC ?
S осн
Площадь боковой поверхности
конуса в два раза больше
площади основания. Найдите
угол между образующей конуса
и плоскостью основания. Ответ
дайте в градусах
S бок Rl
2 2;
S осн R
l
2;
R
BAC 30 ; ABC 60
Ответ: 60 .

39. Дополнительные задачи

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
1. Осевое сечение конуса прямоугольный треугольник.
Найдите площадь боковой поверхности конуса, если его
радиус основания равен R.
Ответ : R
2
2
2. Цилиндр образован вращением прямоугольника
вокруг одной из его сторон. Выразите объем цилиндра
через площадь S прямоугольника и длину С окружности
основания цилиндра.
S C
Ответ :
2
Продолжение
доп. задач
Вернуться к
с/р

40. Дополнительные задачи

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
3. В щар с единичным радиусом вписан конус, образующая
которого равна 3.
Найдите величину угла при вершине осевого сечения
конуса.
Ответ :120
4. В цилиндр, радиус основания которого равен 6, вписан
конус. Основание конуса совпадает с основанием
цилиндра, а вершина конуса совпадает с центром верхнего
основания цилиндра. Площадь боковой поверхности
конуса равна 60 . Найдите площадь боковой поверхности
цилиндра.
Ответ : 96
Вернуться к
с/р

41.

42. Правильно!

ПРАВИЛЬНО!

43. Не верно!

НЕ ВЕРНО!