продолжение Тригонометрические уравнения

1.

Тригонометрические
уравнения (продолжение)

2.

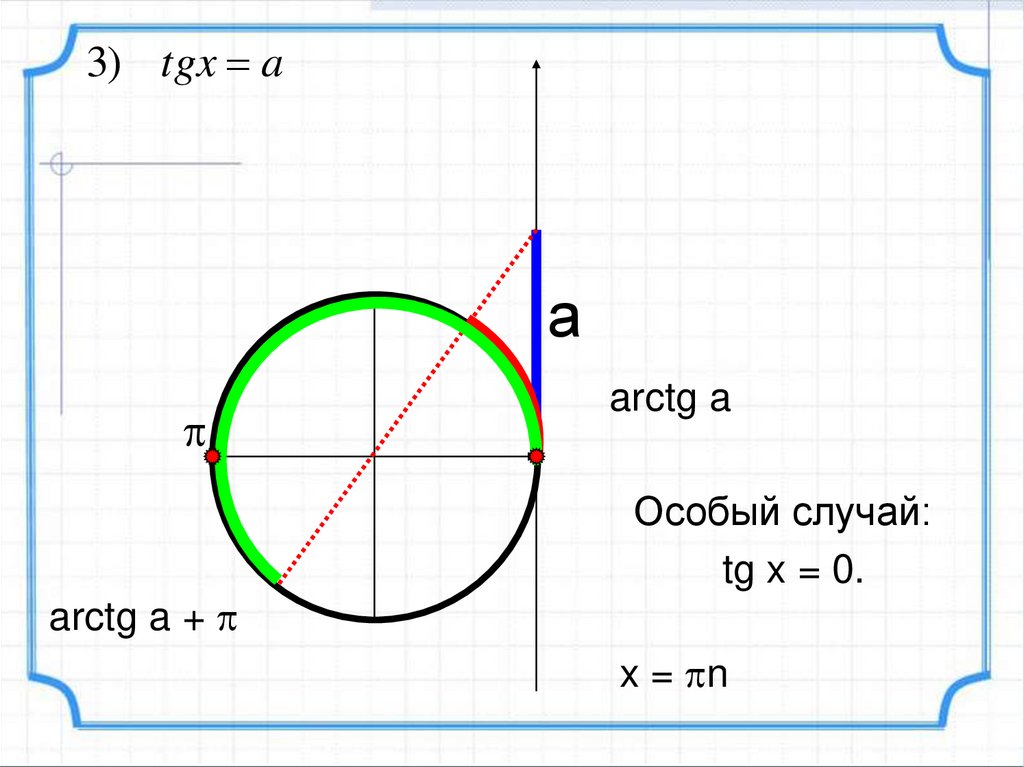
3) tgx a
а
arctg a +
arctg a
Особый случай:
tg x = 0.
x = n

3.

На ; уравнение tgx a имеет единственный
2 2
корень x arctga
Т.к. функция у = tg x периодическая с основным периодом , то
значение функции будет повторяться через k, k Z.
Следовательно,
x = arctg a + πk, kЄZ
- все решения
уравнения tg x = a

4.

Пример 3. Решите уравнение
a) tgx 3 ,
x arctg 3 k , k Z ,
x
б ) tgx 1,
x
4
3
k , k Z .
x arctg 1 k , k Z.
k , k Z .
в ) ctgx 3 ,
1
tgx
,
3
1
x arctg
k , k Z ,
3
x
6
k , k Z .

5.

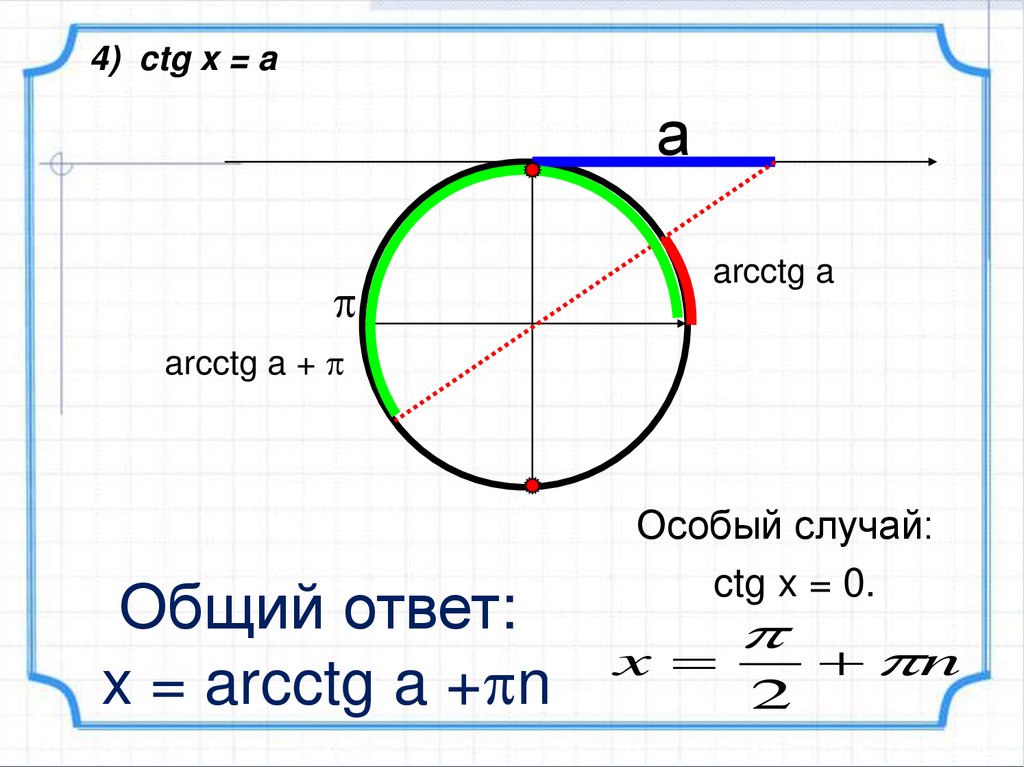
4) ctg x = a
а
arcctg a
arcctg a +
Общий ответ:
x = arcctg a + n
Особый случай:
ctg x = 0.
x
2
n

6.

Арктангенсом числа a R называется такое число
[- /2; /2], тангенс которого равен a:
arctg a = , если tg = a и - /2 /2
Арккотангенсом числа a R называется такое
число [0; ], котангенс которого равен a:
arcctg a = , если ctg = a и 0