1. Презентация динамика

1.

СИЛЫ
В
МЕХАНИКЕ
1

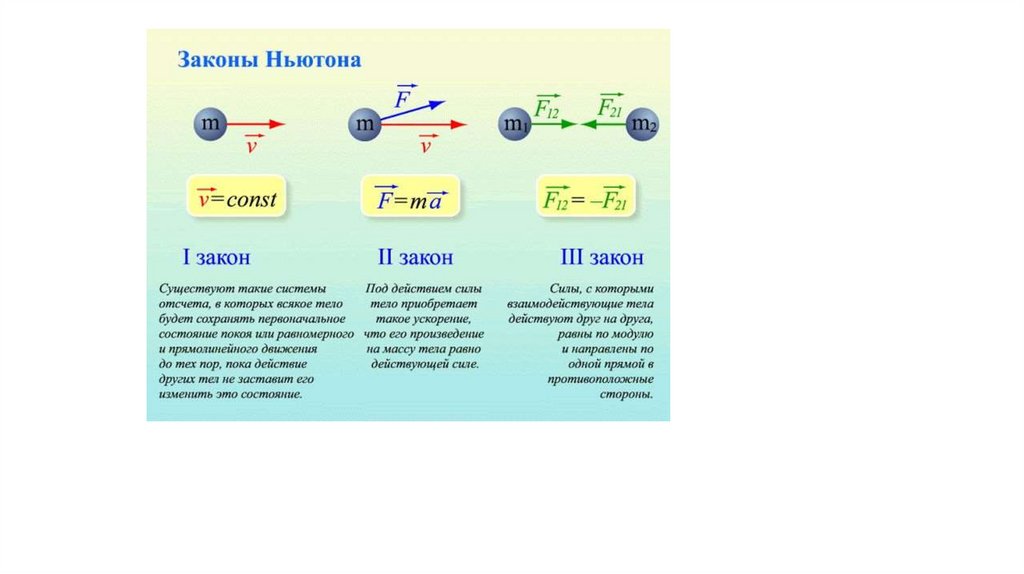
2.

3. В механике используется принцип освобождаемости связей

• Несвободное тело можно считать свободным, если действие тел
заменить их cвязями.
3

4.

Сила тяжести
Сила тяжести – сила,
с которой тело притягивается к земле.
FT mg
Направление
– вертикально вниз.
Точка приложения
– центр масс тела.
Величина – Fт = mg.
4

5.

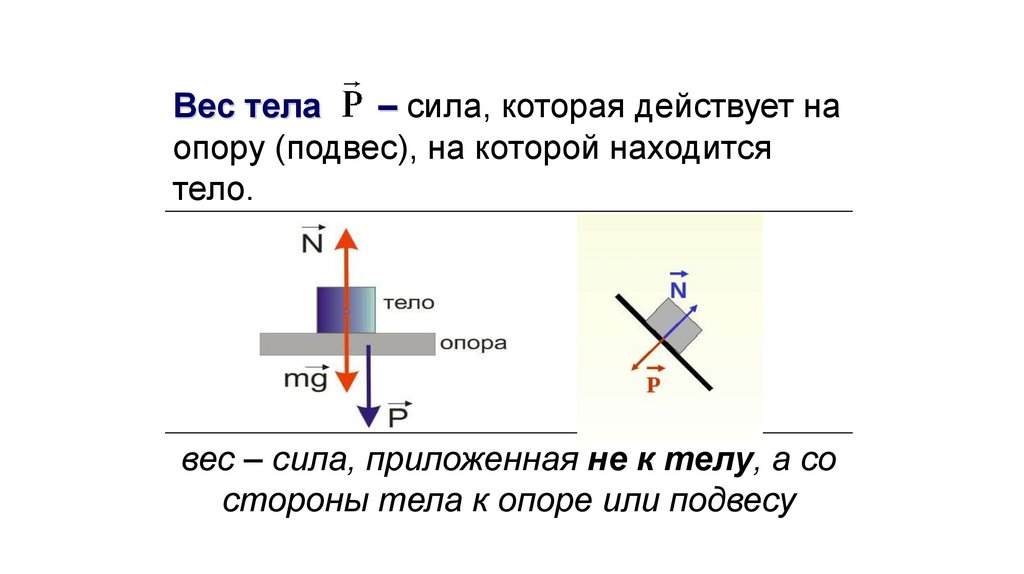
Вес тела
– сила, которая действует на
опору (подвес), на которой находится
тело.
вес – сила, приложенная не к телу, а со
стороны тела к опоре или подвесу

6.

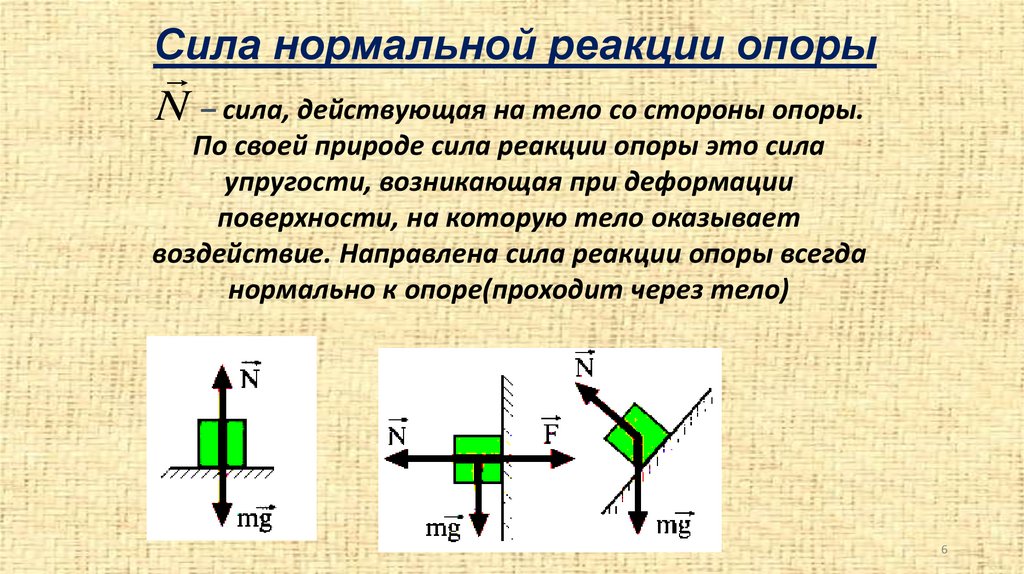
Сила нормальной реакции опоры
N – сила, действующая на тело со стороны опоры.
По своей природе сила реакции опоры это сила
упругости, возникающая при деформации
поверхности, на которую тело оказывает
воздействие. Направлена сила реакции опоры всегда
нормально к опоре(проходит через тело)
N
6

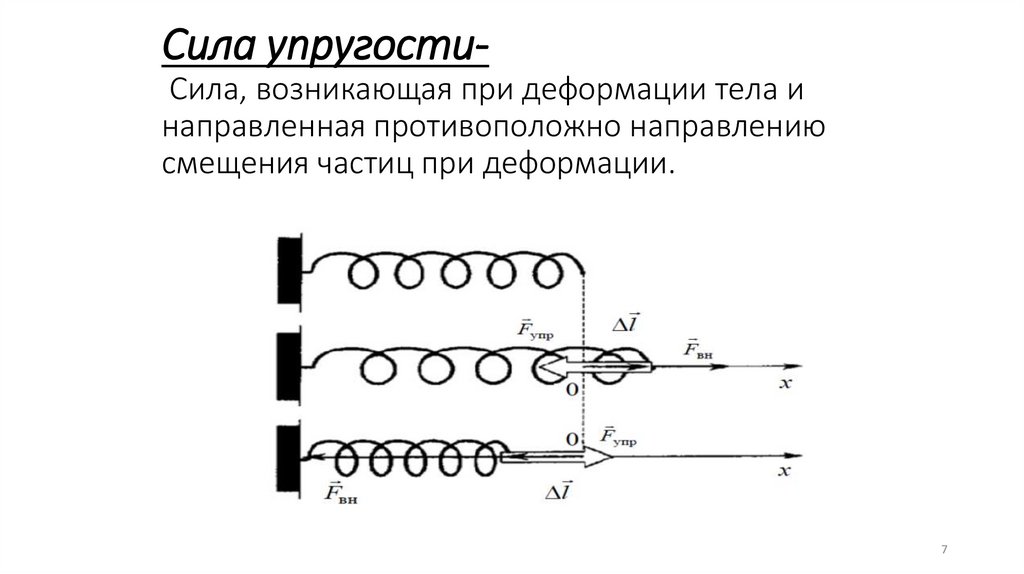
7. Сила упругости- Сила, возникающая при деформации тела и направленная противоположно направлению смещения частиц при деформации.

Сила упругостиСила, возникающая при деформации тела и
направленная противоположно направлению
смещения частиц при деформации.
7

8.

Сила трения скольжения
Сила трения - сила, возникающая в плоскости
касания тел при их относительном
перемещении.
Сила трения зависит от силы давления тел
друг на друга, от материалов трущихся
поверхностей, от скорости относительного
движенияи не зависит от площади
соприкосновения
8

9.

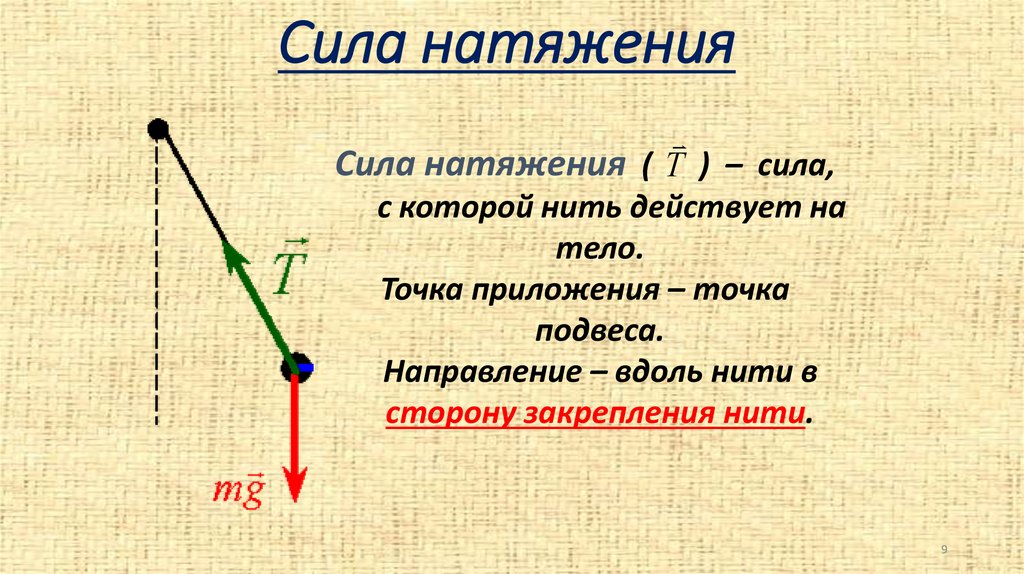
Сила натяжения
Сила натяжения ( Т ) – сила,
с которой нить действует на
тело.
Точка приложения – точка
подвеса.
Направление – вдоль нити в
сторону закрепления нити.
9

10.

2 занятие
Динамика
вращательного
движения.

11.

11

12.

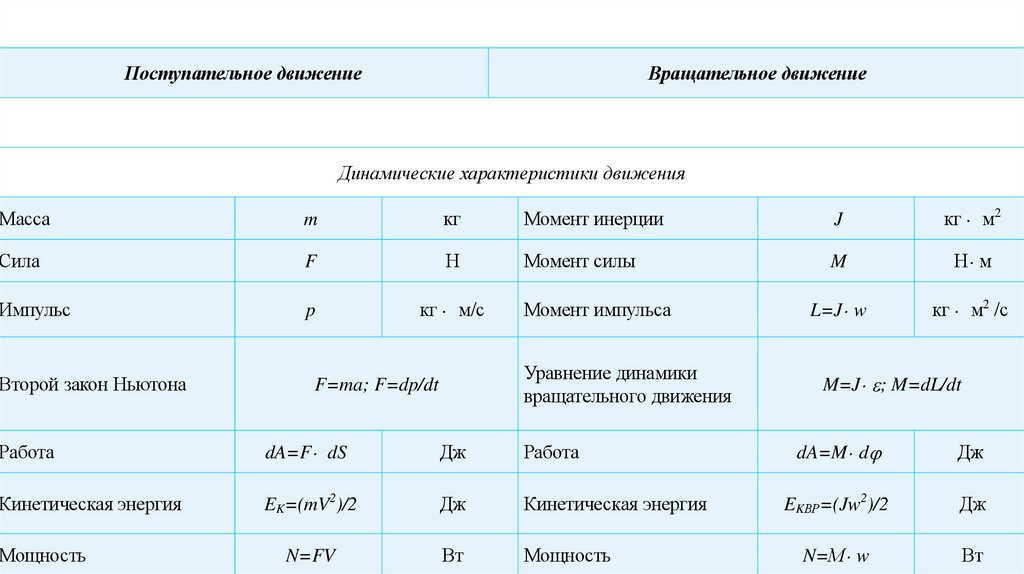
Поступательное движение
Вращательное движение
Динамические характеристики движения
Масса
m
кг
Момент инерции
J
кг м2
Сила
F
Н
Момент силы
M
Н м
Импульс
p
кг м/с
Момент импульса
L=J w
кг м2 /с
Второй закон Ньютона
F=ma; F=dp/dt
Уравнение динамики
вращательного движения
M=J e; M=dL/dt
Работа
dA=F dS
Дж
Работа
dA=M dj
Дж
Кинетическая энергия
EK=(mV2)/2
Дж
Кинетическая энергия
EKВР=(Jw2)/2
Дж
N=FV
Вт
Мощность
Мощность
N=М w
12
Вт

13. Основные физические величины динамики вращательного движения

•момент инерции,
• момент силы,
• момент импульса.
13

14.

По аналогии с массой и поступательным движением момент инерции – это мера
инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при
вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в
килограммах, умноженных на квадратный метр.
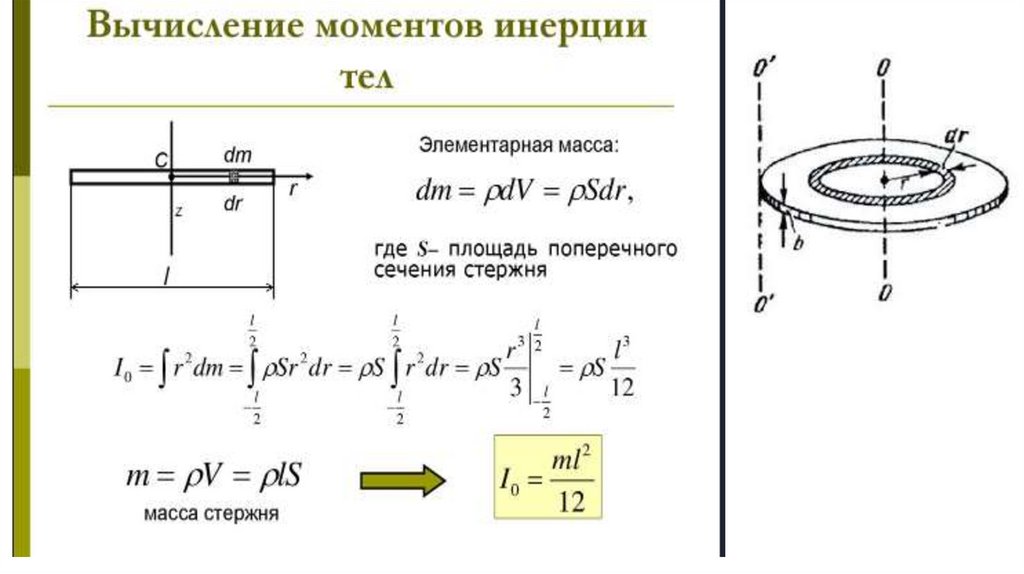
Как посчитать момент инерции? Есть общая формула, по которой в физике
вычисляется момент инерции любого тела.
Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет
равен сумме произведений этих элементарных масс на квадрат расстояния до оси
вращения.
J=mr2

15.

15

16.

17.

18.

19.

20.

21.

22.

22

23.

24.

25.

26.

27.

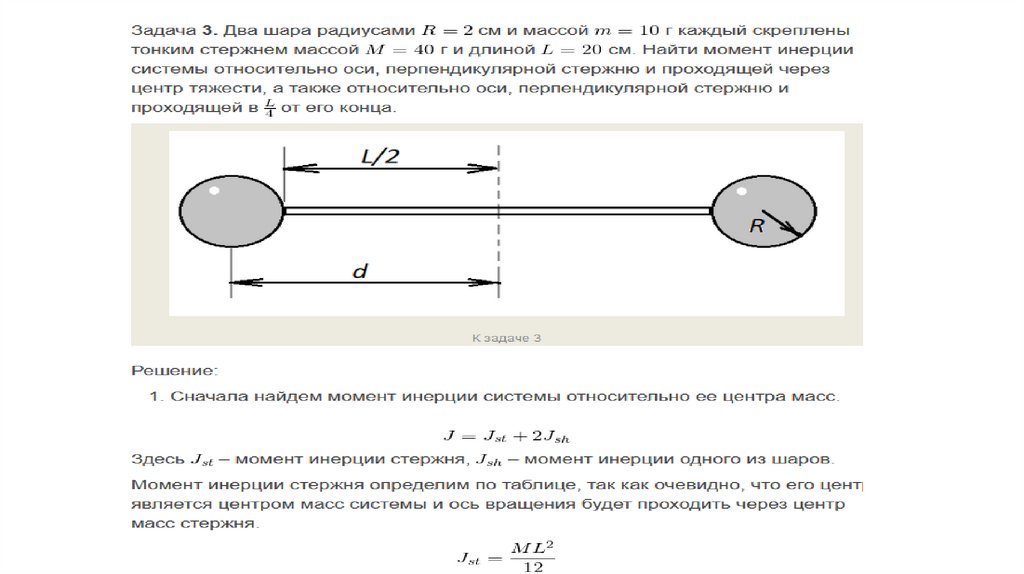
1. Определить момент инерции J тонкого однородного стержня длиной l = 50 см и массой m =
360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня;
2) точку, отстоящую от конца стержня на 1/6 его длины.

28.

29.

29

30.

30

31.

31

32.

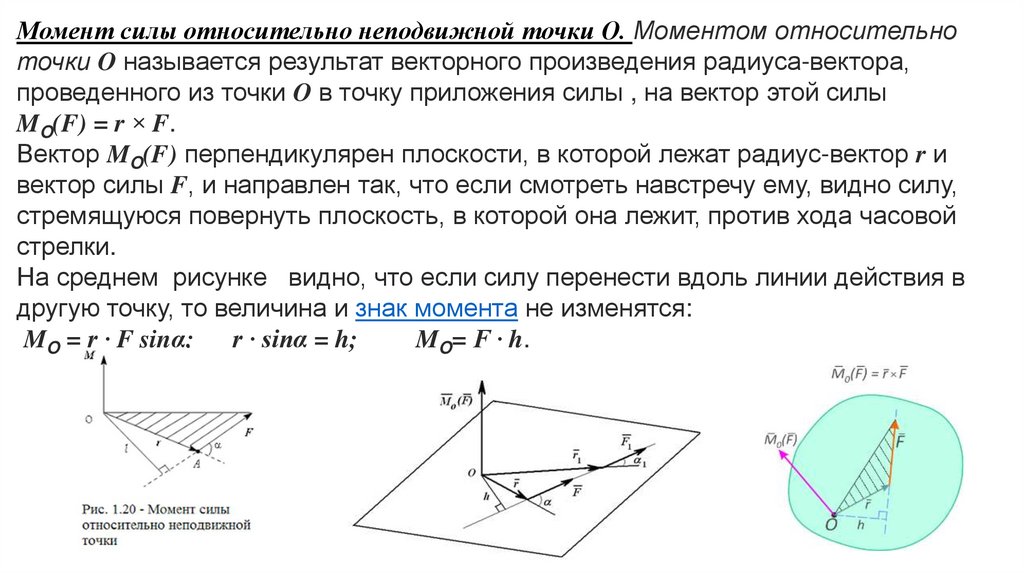
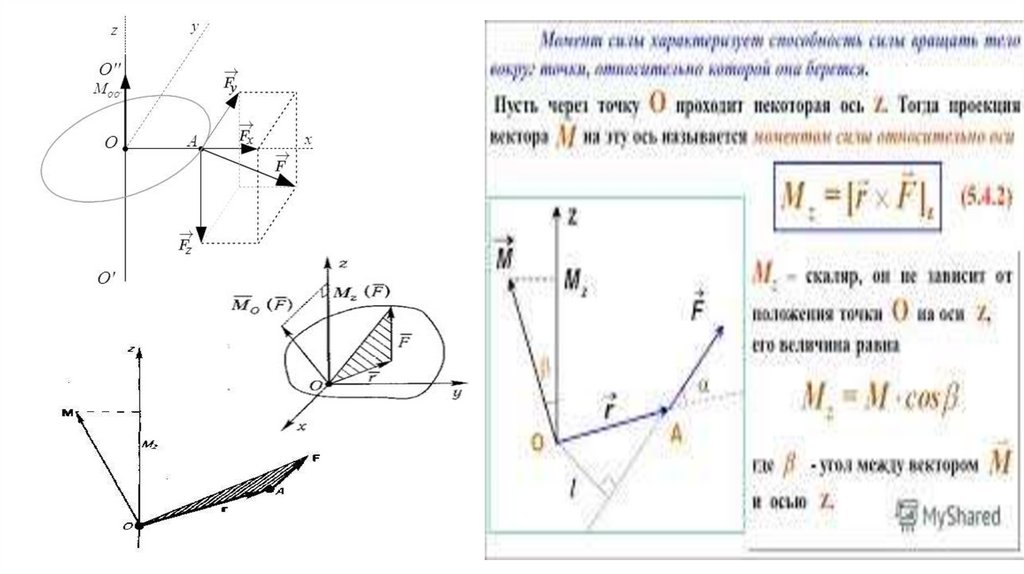
Момент силы относительно неподвижной точки О. Моментом относительно
точки O называется результат векторного произведения радиуса-вектора,
проведенного из точки O в точку приложения силы , на вектор этой силы
MO(F) = r × F.
Вектор MO(F) перпендикулярен плоскости, в которой лежат радиус-вектор r и
вектор силы F, и направлен так, что если смотреть навстречу ему, видно силу,
стремящуюся повернуть плоскость, в которой она лежит, против хода часовой
стрелки.
На среднем рисунке видно, что если силу перенести вдоль линии действия в
другую точку, то величина и знак момента не изменятся:
MO = r ∙ F sinα; r ∙ sinα = h;
MO= F ∙ h.

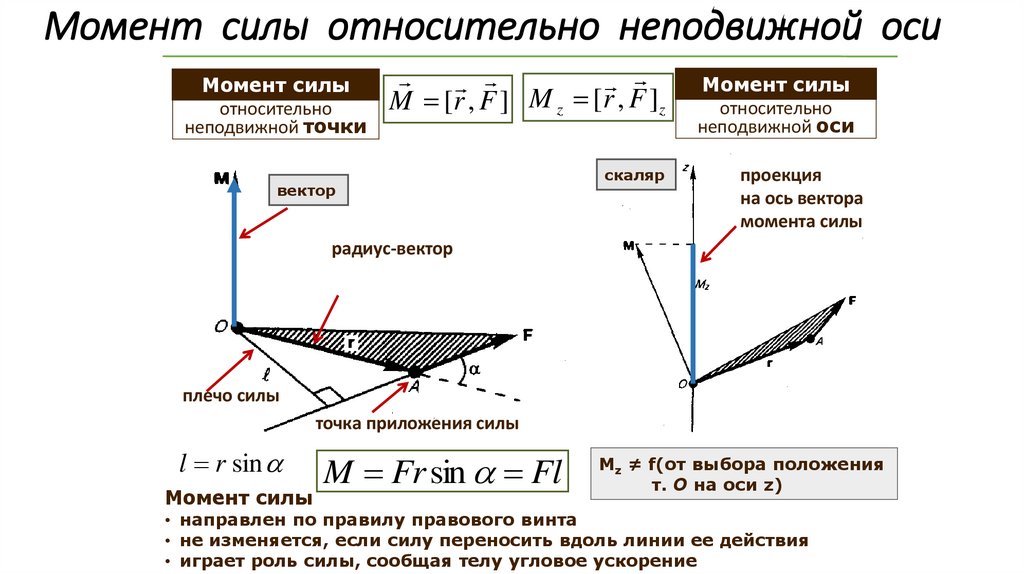
33. Момент силы относительно неподвижной оси

Момент силы
относительно
неподвижной точки
M [r , F ] M z [r , F ]z
вектор
скаляр
Момент силы
относительно
неподвижной оси
проекция
на ось вектора
момента силы
радиус-вектор
плечо силы
точка приложения силы
l r sin
Момент силы
M Fr sin Fl
Мz ≠ f(от выбора положения
т. О на оси z)
• направлен по правилу правового винта
• не изменяется, если силу переносить вдоль линии ее действия
• играет роль силы, сообщая телу угловое ускорение

34.

35.

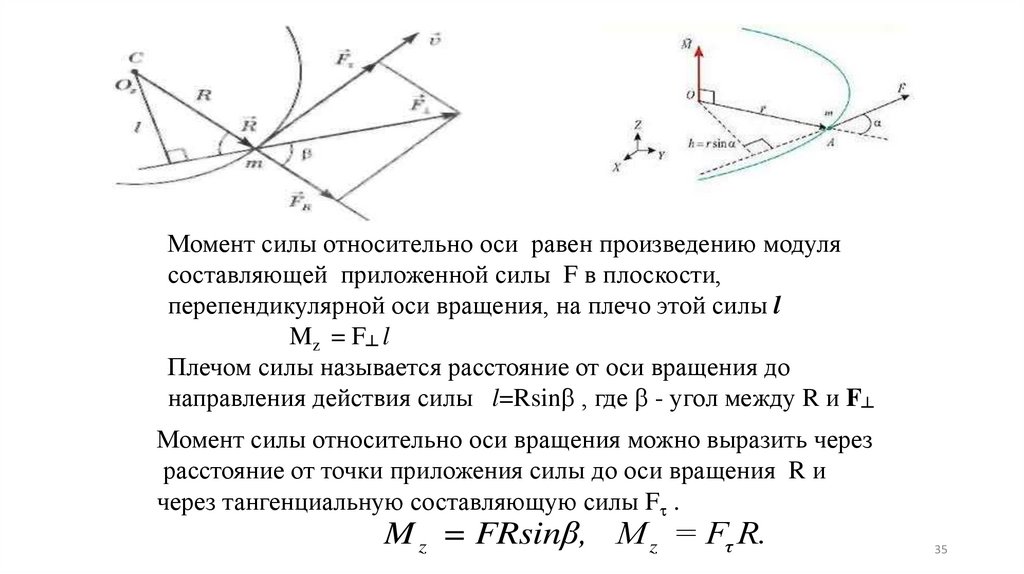
Момент силы относительно оси равен произведению модуля
составляющей приложенной силы F в плоскости,
перепендикулярной оси вращения, на плечо этой силы l
Mz = F┴ l
Плечом силы называется расстояние от оси вращения до
направления действия силы l=Rsin , где - угол между R и F┴
Момент силы относительно оси вращения можно выразить через
расстояние от точки приложения силы до оси вращения R и
через тангенциальную составляющую силы F .
M z = FRsinβ, M z = Fτ R.
35

36. Второй закон Ньютона для вращения

37.

38.

38

39.

40.

41.

42. ГРУЗЫ НА НИТИ

Г

43.

В задачах для грузов( груз 1 и 2 ), подвешенных на нити,
перекинутой чеоез вращающейся блок (его масса не равна
нулю или в задаче задан вид блока-момент инерции не равен
нулю) принято считать, что
1. Нить невесома- ускорение в любой точке нити одинаково
(справа и слева от блока)
2. Нить нерастяжима-сила натяжения нити от блока до
закрепленного груза одинакова , но( см.п.4)
3. Отсутствует проскальзывание нити по блоку
4. Силы натяжения нити по разные стороны блока имеют
различные значения, за счет этого блок приводится в
движение (вращается).

44.

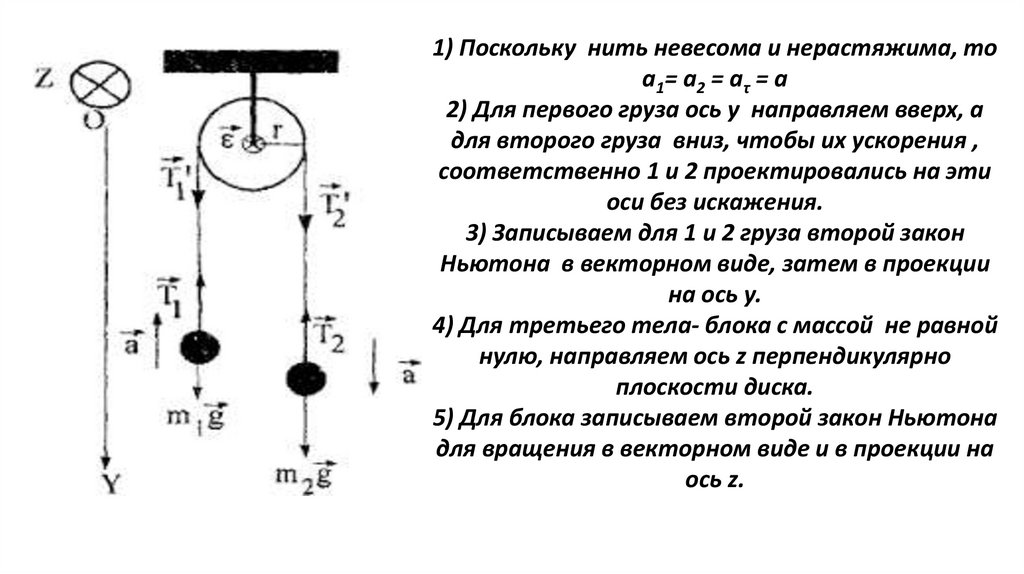
1) Поскольку нить невесома и нерастяжима, то
а1= а2 = аτ = а
2) Для первого груза ось у направляем вверх, а
для второго груза вниз, чтобы их ускорения ,
соответственно 1 и 2 проектировались на эти
оси без искажения.
3) Записываем для 1 и 2 груза второй закон
Ньютона в векторном виде, затем в проекции
на ось у.
4) Для третьего тела- блока с массой не равной
нулю, направляем ось z перпендикулярно
плоскости диска.
5) Для блока записываем второй закон Ньютона
для вращения в векторном виде и в проекции на
ось z.