Similar presentations:
1 геометрия 8 23.12.2025
1. § 1. Площадь параллелограмма, треугольника и трапеции.
51. Площадь параллелограмма.55. Площадь треугольника .
53. Площадь трапеции.
2.
Площадь параллелограмма3. Задачи нашего урока
• доказать теорему оплощади
параллелограмма и
вывести следствие из
неё; использовать их
при решении задач.
• Будут выведены формулы,
по которым можно
вычислить площадь
параллелограмма.
• Все эти формулы широко
используются не только при
решении геометрических
задач, но и в обыденной
практике, при различных
расчётах, связанных с
техникой, производством,
конструированием.
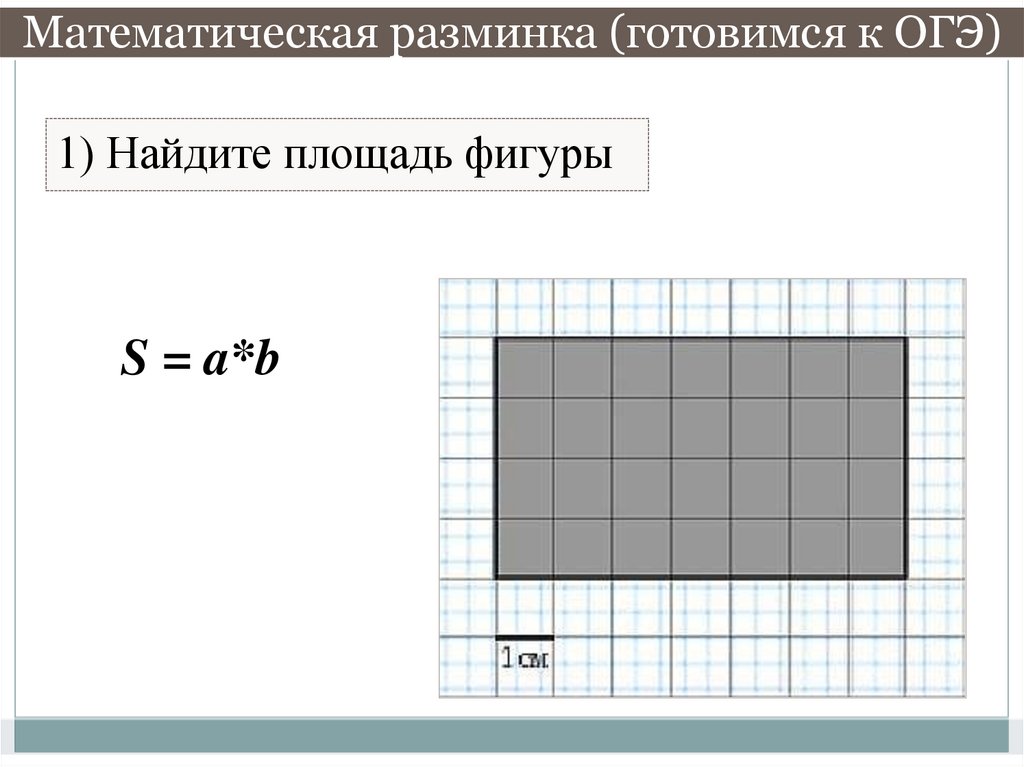
4. Математическая разминка (готовимся к ОГЭ)
1) Найдите площадь фигурыS = a*b
5. 2) Периметр квадрата равен 40. Найдите площадь квадрата.
P = 4*aa= ¼*P
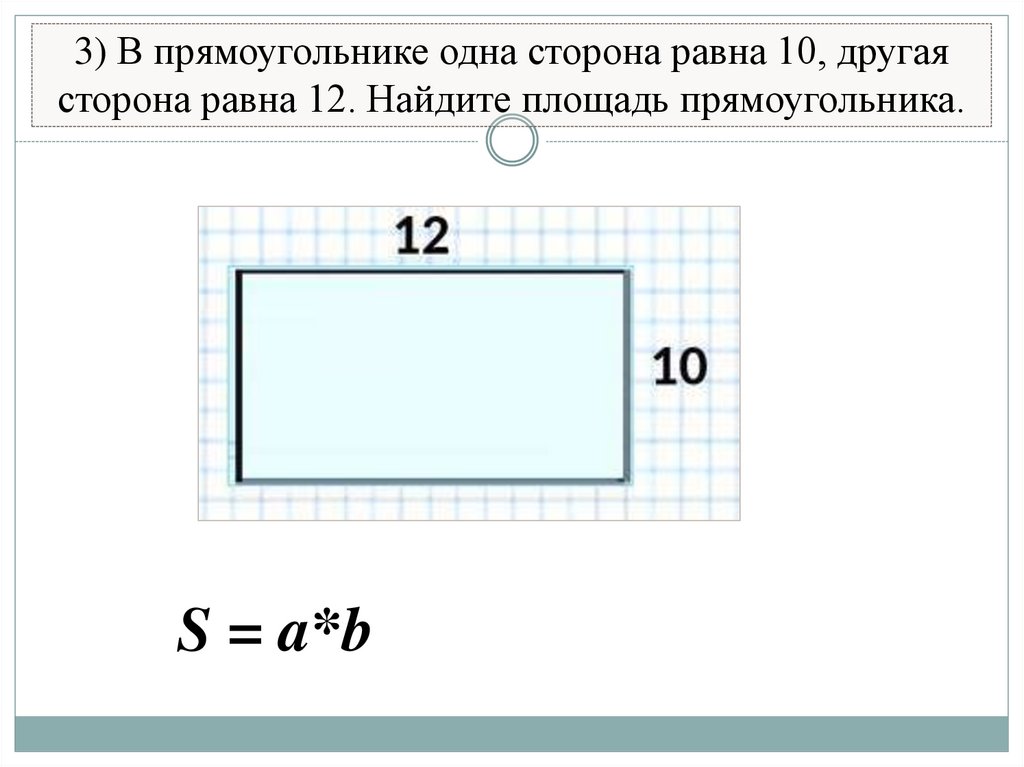
6. 3) В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3) В прямоугольнике одна сторона равна 10, другаясторона равна 12. Найдите площадь прямоугольника.
S = a*b
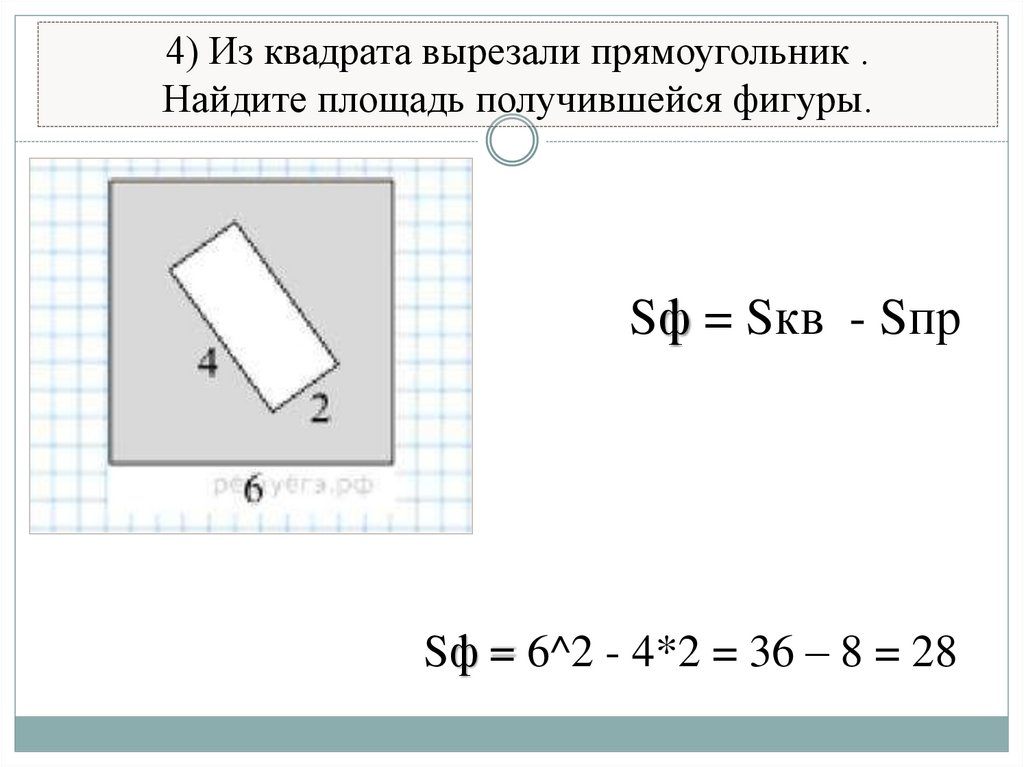
7. 4) Из квадрата вырезали прямоугольник . Найдите площадь получившейся фигуры.
Sф = Sкв - SпрSф = 6^2 - 4*2 = 36 – 8 = 28
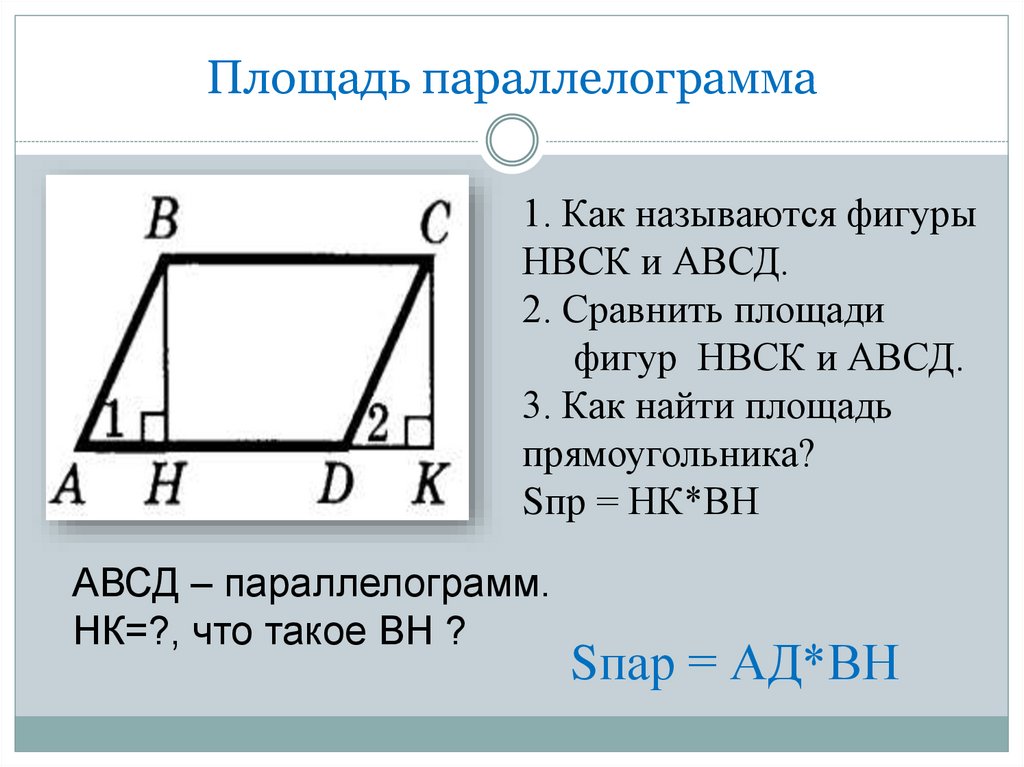
8. Площадь параллелограмма
1. Как называются фигурыНВСК и АВСД.
2. Сравнить площади
фигур НВСК и АВСД.
3. Как найти площадь
прямоугольника?
Sпр = НК*ВН
АВСД – параллелограмм.
НК=?, что такое ВН ?
Sпар = АД*ВН
9. Площадь параллелограмма
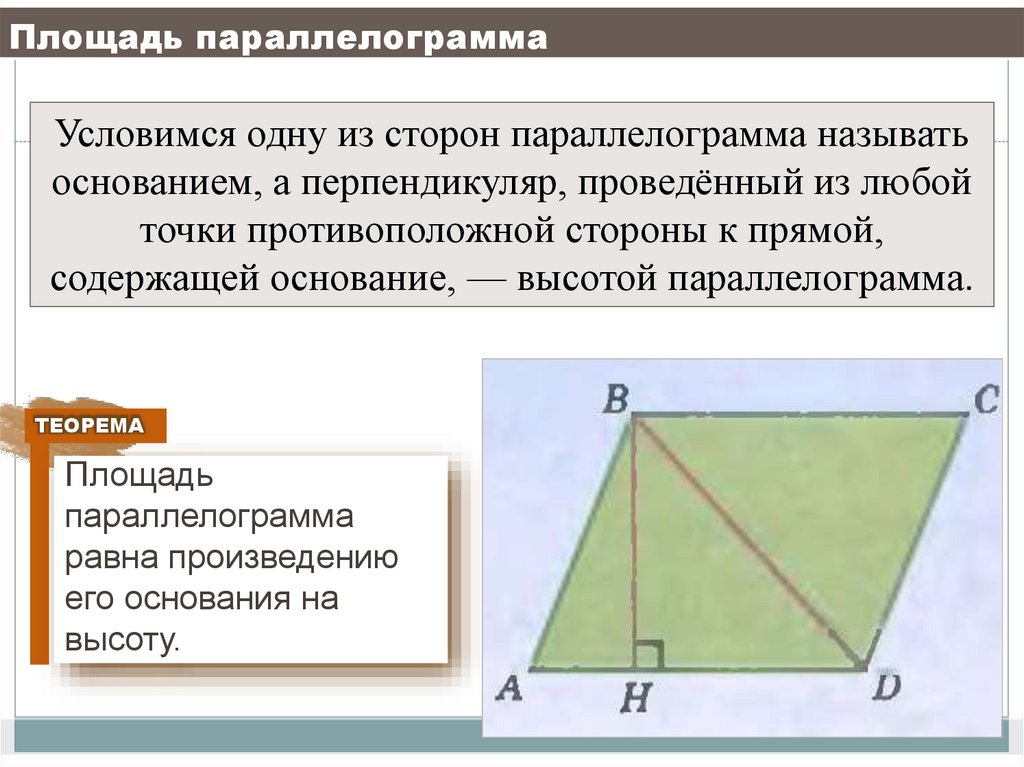
Условимся одну из сторон параллелограмма называтьоснованием, а перпендикуляр, проведённый из любой
точки противоположной стороны к прямой,
содержащей основание, — высотой параллелограмма.
ТЕОРЕМА
Площадь
параллелограмма
равна произведению
его основания на
высоту.
10. Теорема (формула площади параллелограмма по стороне и высоте)
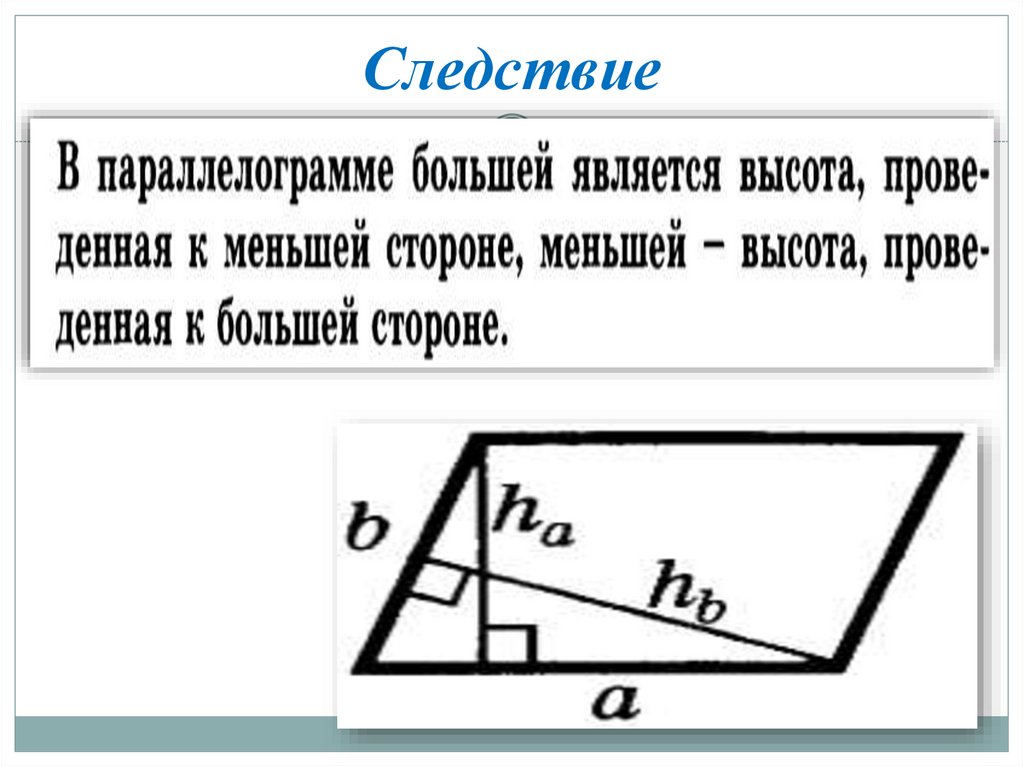
11. Следствие
12. Метод вспомогательных площадей (метод площадей)
13. Повторение материала из 7 класса
1. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.2. СООТНОШЕНИЯ СТОРОН В
ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
14. Смежные углы.
15. Вертикальные углы.
16. Следствия.
17.
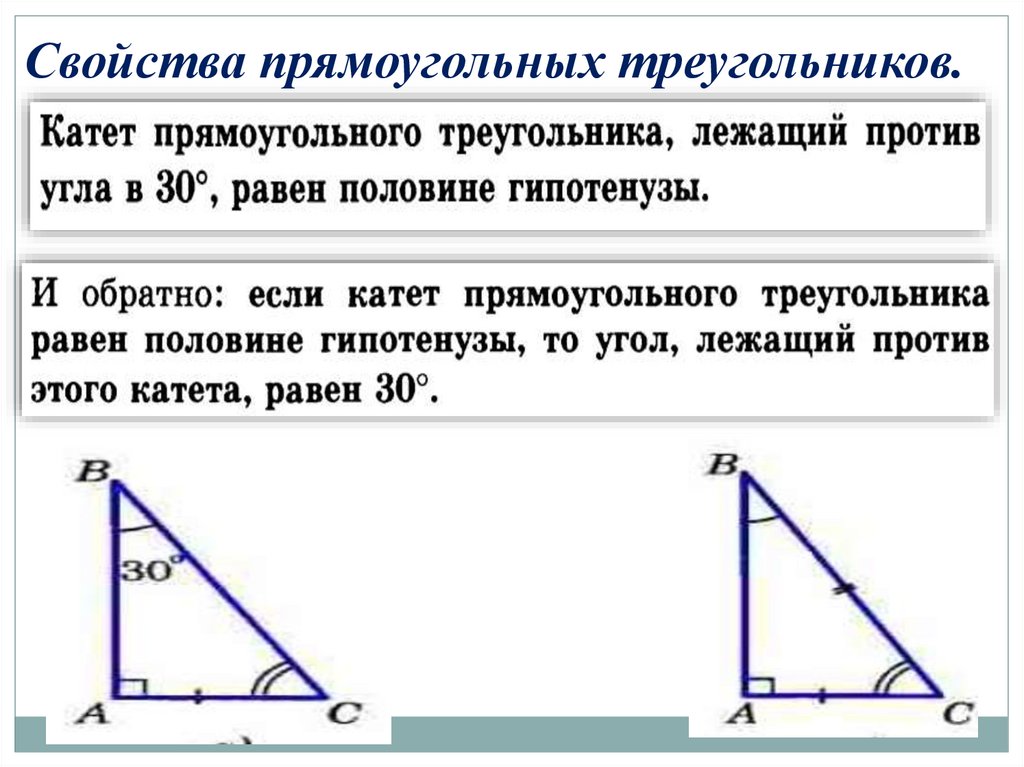
18. Свойства прямоугольных треугольников.
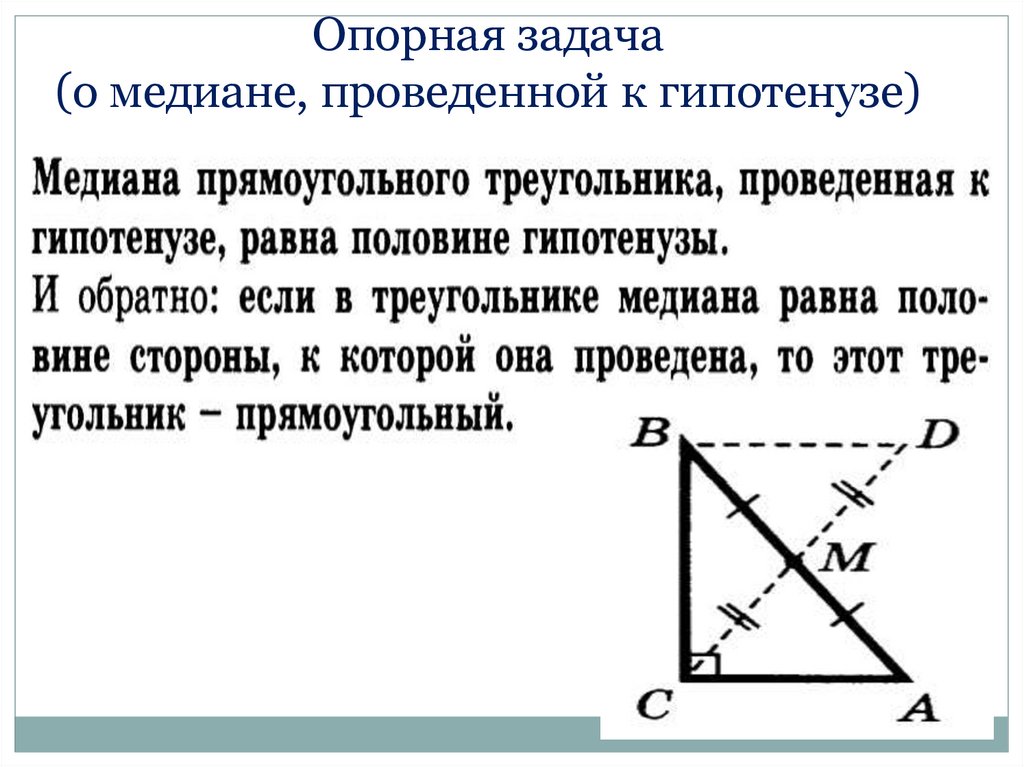
19. Опорная задача (о медиане, проведенной к гипотенузе)
20. Решение задач
21.
22.
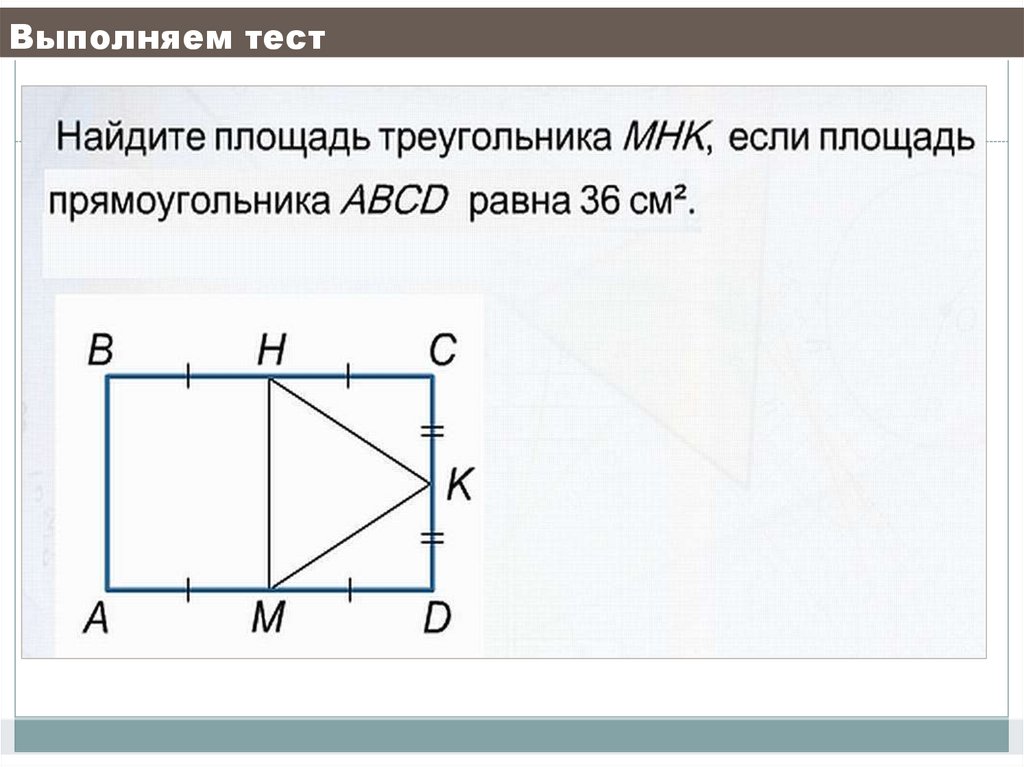
23. Выполняем тест
24. Домашнее задание:
Изучить пункт 52; выполнить задание на выборНа 3 № 459 (а), 460
На 4, 5 1. Пусть а – основание, h – высота, а S –
площадь параллелограмма. Найдите а, если S=45
см2, h=7,5 см.
2. Смежные стороны параллелограмма 12 см и 16
см, а его тупой угол 150. Найдите площадь
параллелограмма.
25.
Площадь треугольника26. Задачи нашего урока
• вывести несколькоформул площади
треугольника;
• рассмотреть задачи,
в которых
используются эти
формулы.
• Будут выведены формулы, по
которым можно вычислить
площади треугольника.
• Некоторые из этих формул вы
уже знаете.
• Все эти формулы широко
используются не только при
решении геометрических задач,
но и в обыденной практике, при
различных расчётах, связанных с
техникой, производством,
конструированием.
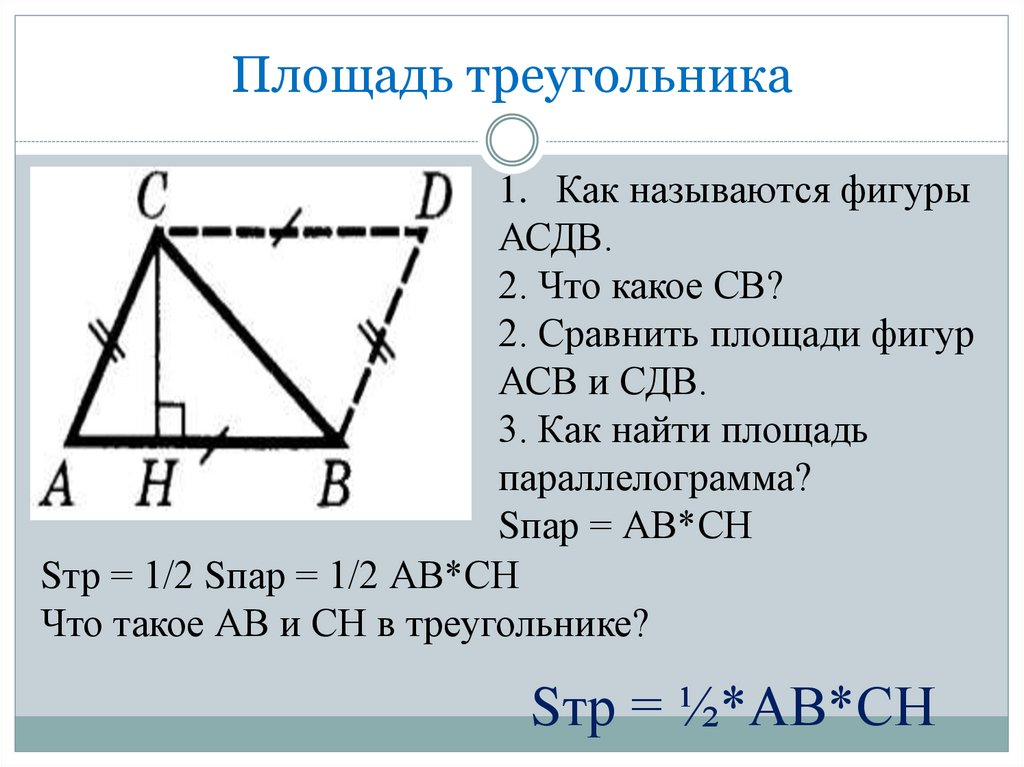
27. Площадь треугольника
1. Как называются фигурыАСДВ.
2. Что какое СВ?
2. Сравнить площади фигур
АСВ и СДВ.
3. Как найти площадь
параллелограмма?
Sпар = АВ*СН
Sтр = 1/2 Sпар = 1/2 АВ*СН
Что такое АВ и СН в треугольнике?
Sтр = ½*АВ*СН
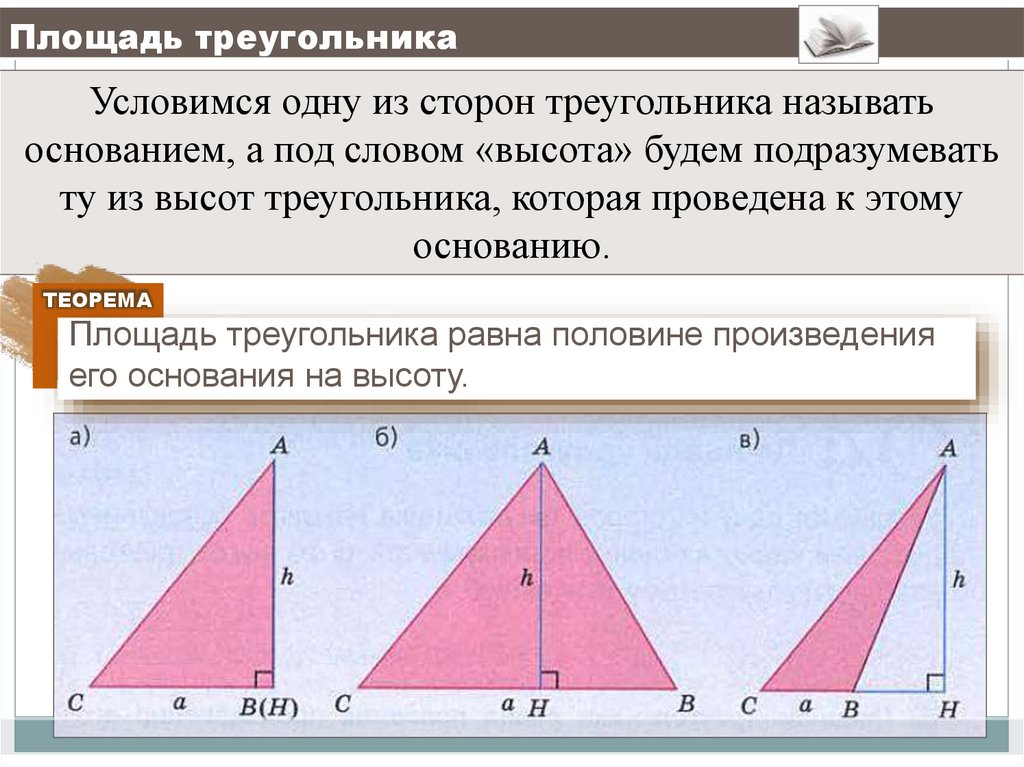
28. Площадь треугольника
Условимся одну из сторон треугольника называтьоснованием, а под словом «высота» будем подразумевать
ту из высот треугольника, которая проведена к этому
основанию.
ТЕОРЕМА
Площадь треугольника равна половине произведения
его основания на высоту.
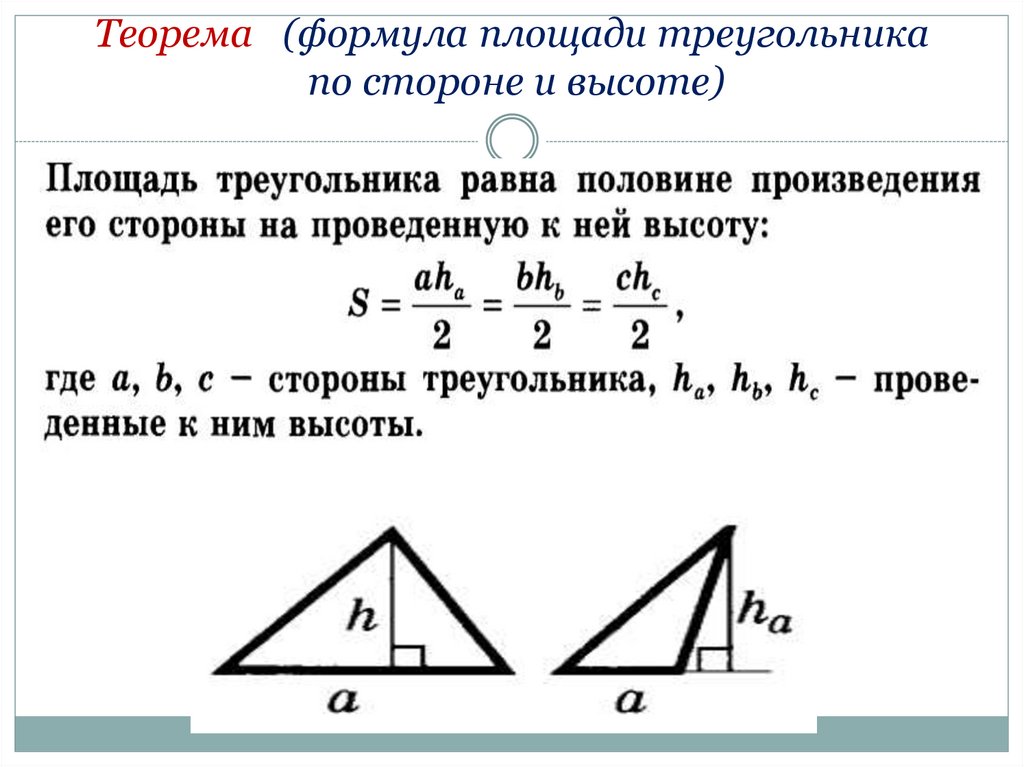
29. Теорема (формула площади треугольника по стороне и высоте)
30.
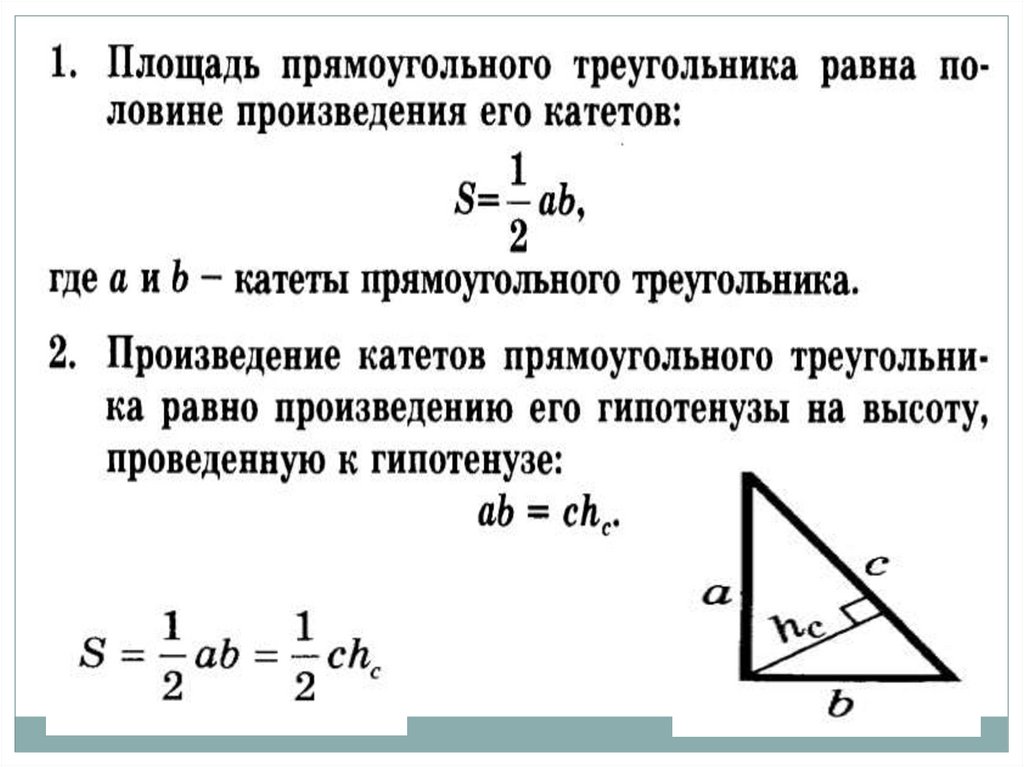
31. Следствия.
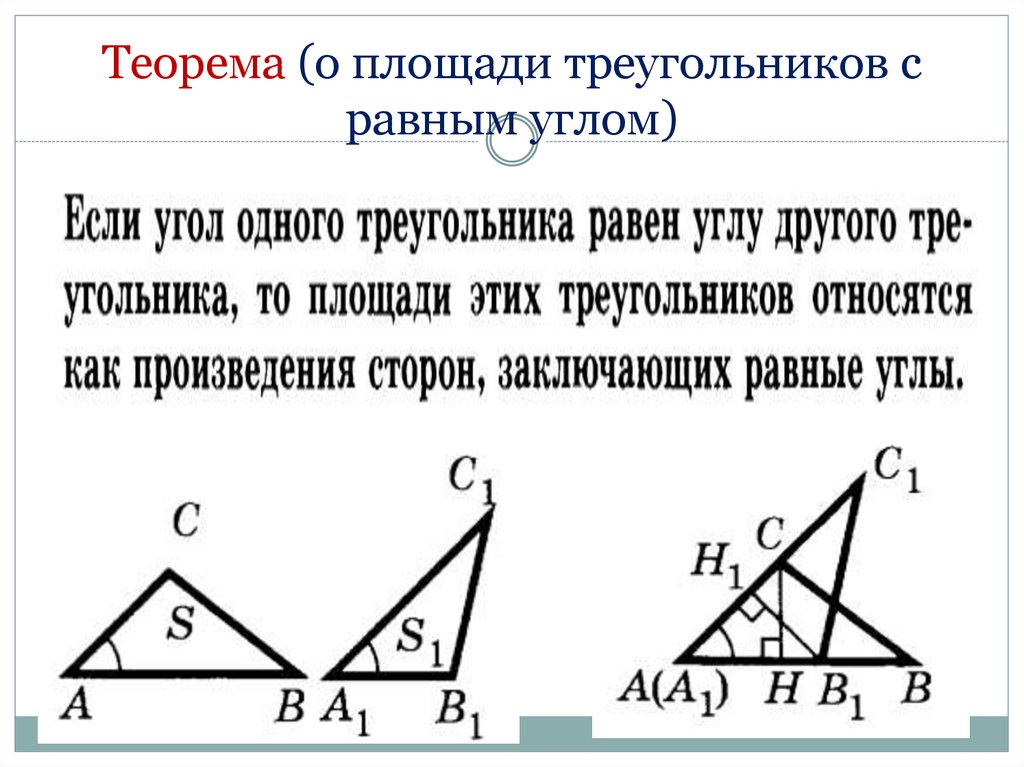
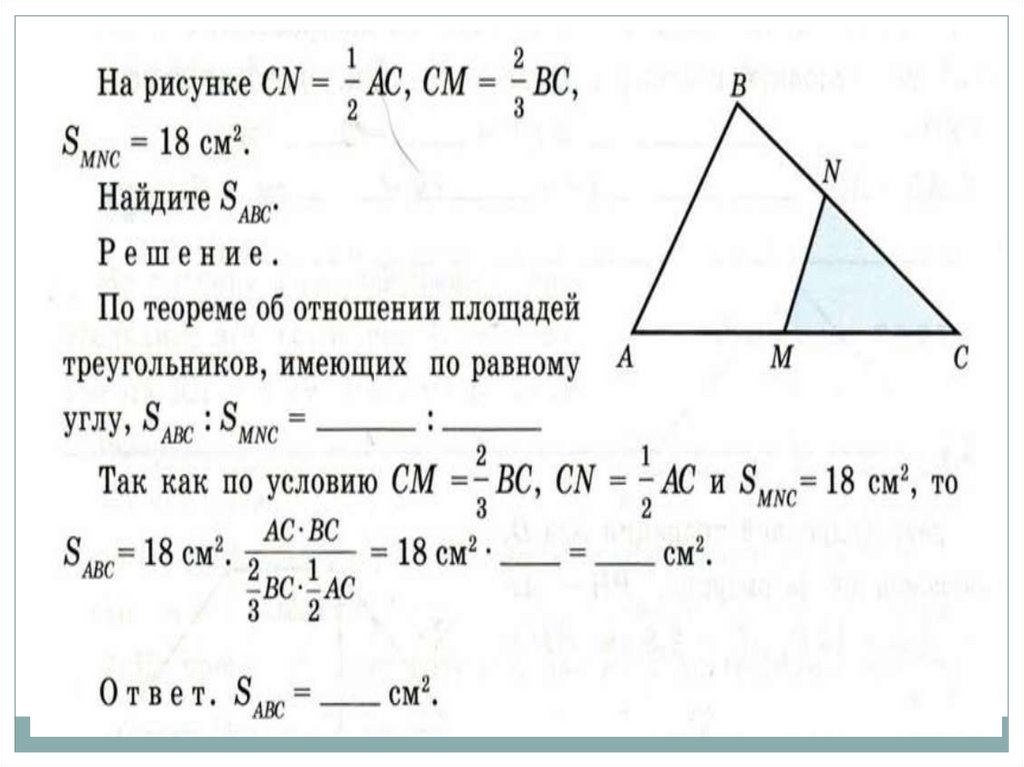
32. Теорема (о площади треугольников с равным углом)
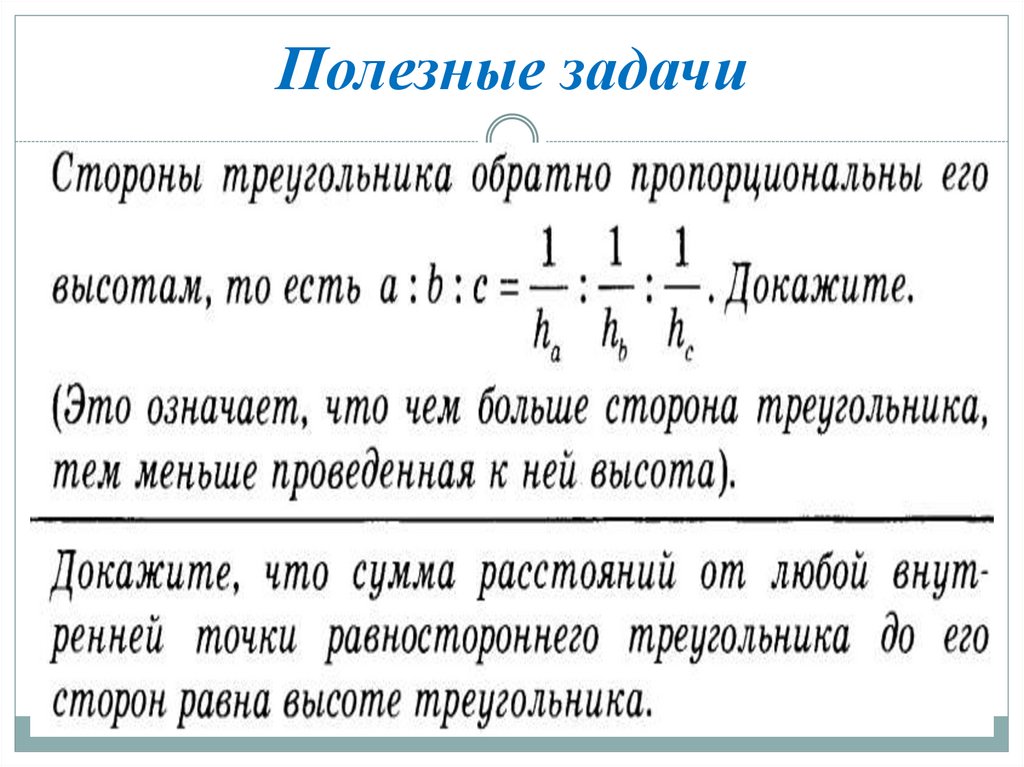
33. Полезные задачи
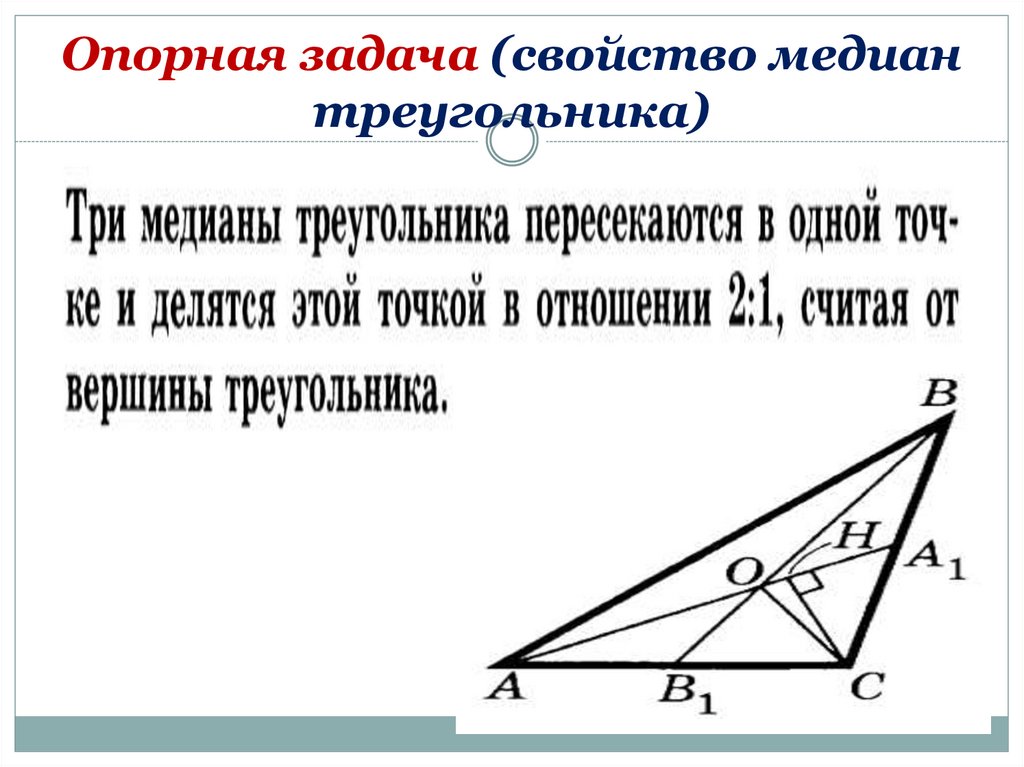
34. Опорная задача (свойство медиан треугольника)
35.
36.
37. Полезные задачи.
38.
Решениезадач
39.
Решениезадач
40.
41. Знаменитый треугольник
С понятием треугольника мывстречаемся во многих сферах
деятельности человека и в
повседневной жизни: в
архитектуре, строительстве и
даже в медицине. Вспомните,
например, из уроков географии
о загадочном месте в
Атлантическом океане,
расположенном между
Бермудскими островами,
государством Пуэрто-Рико и
полуостровом Флорида, по
форме напоминающем
геометрическую фигуру
треугольник.
Как называется это место?
Речь идет о «бермудском
треугольнике» или так называемом
«треугольнике проклятых».
Загадочность
??? этого места
заключается в том, что в нем
бесследно исчезают корабли и
самолеты, изменяется
пространство и время. Тайны
«бермудского треугольника» не
раскрыты до конца и по сей день.
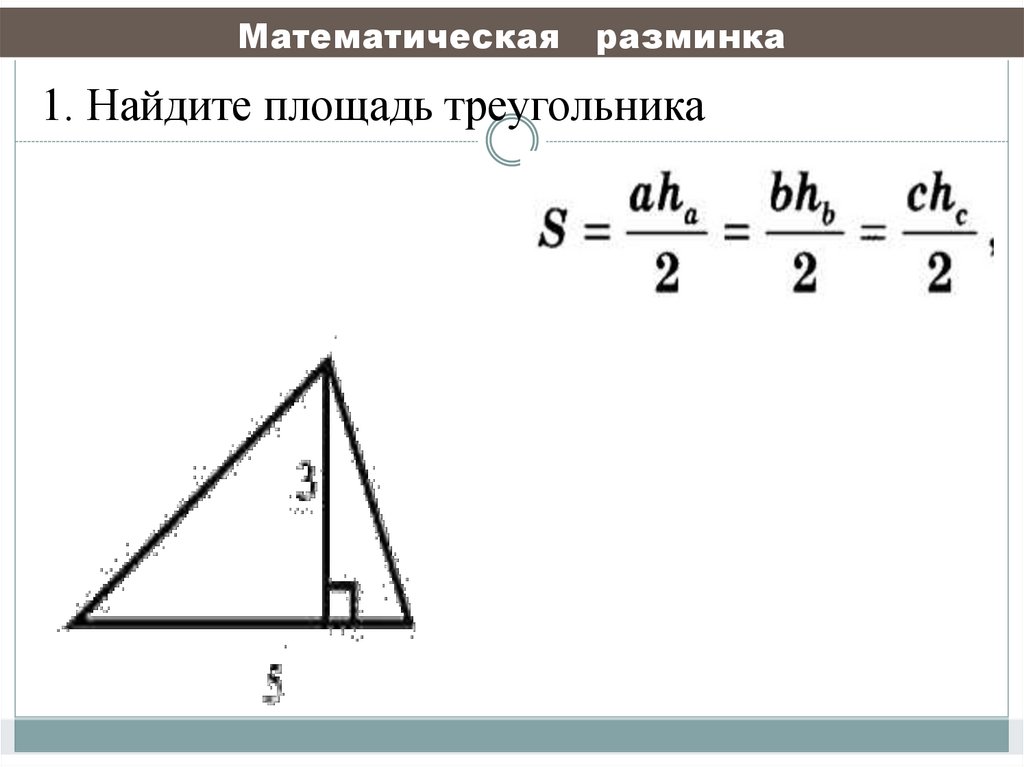
42. Математическая разминка
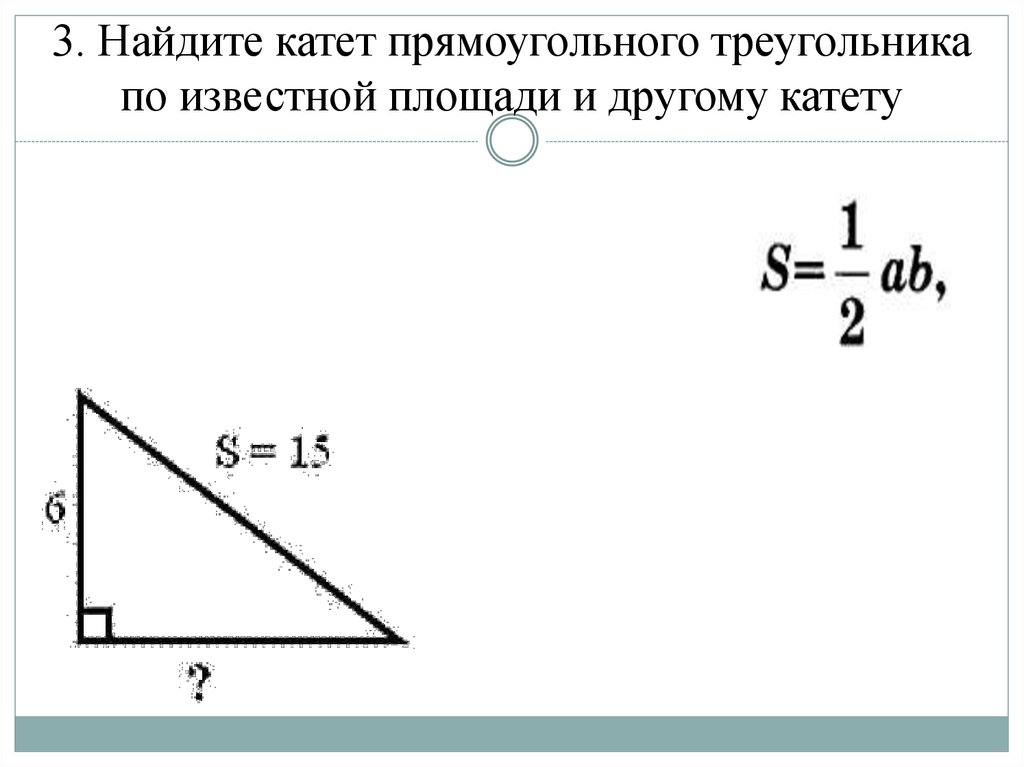
1. Найдите площадь треугольника43. 3. Найдите катет прямоугольного треугольника по известной площади и другому катету
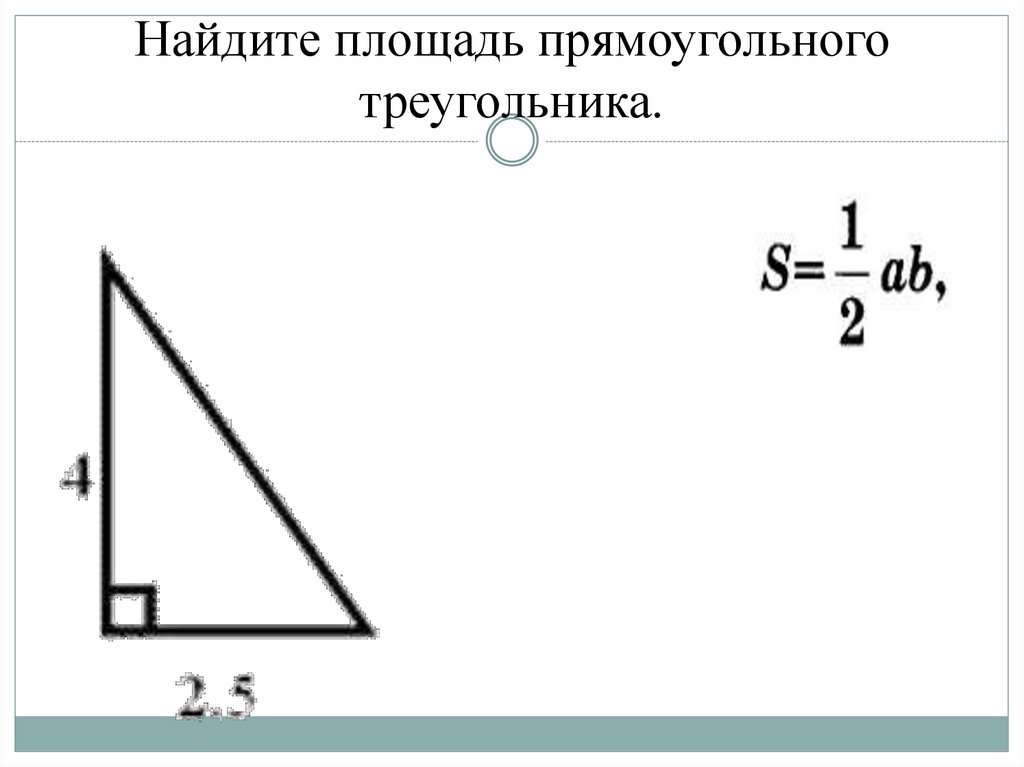
44. Найдите площадь прямоугольного треугольника.
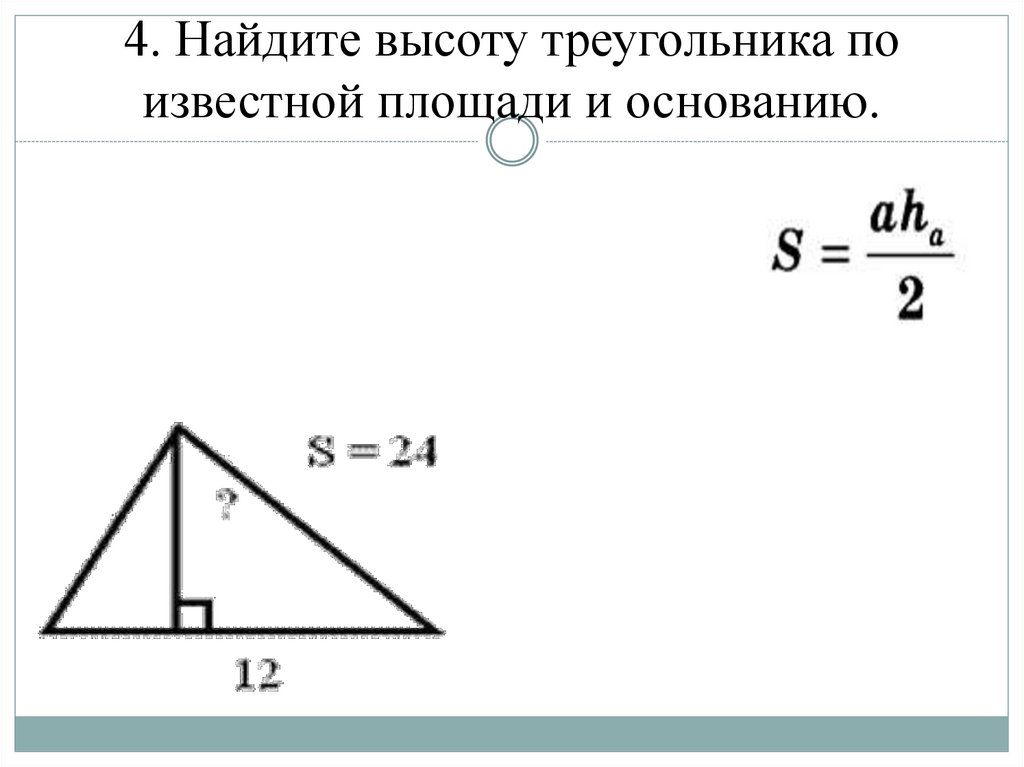
45. 4. Найдите высоту треугольника по известной площади и основанию.
46. Площадь трапеции
47. Задачи нашего урока
• вывести формулуплощади трапеции;
• использовать её при
решении задач;
• Будет выведена формула, по
которой можно вычислить
площадь трапеции.
• Все эти формулы широко
используются не только при
решении геометрических задач,
но и в обыденной практике, при
различных расчётах, связанных
с техникой, производством,
конструированием.
48. Математическая разминка
• Дать определение трапеции.• Какие виды трапеций вы знаете?
• На доске изображена трапеция ABCD. Укажите на
данном чертеже, что является основаниями, боковой
стороной, средней линией.
• Что такое площадь фигуры?
• Сформулируйте свойства площади для простых фигур.
B
A
C
D
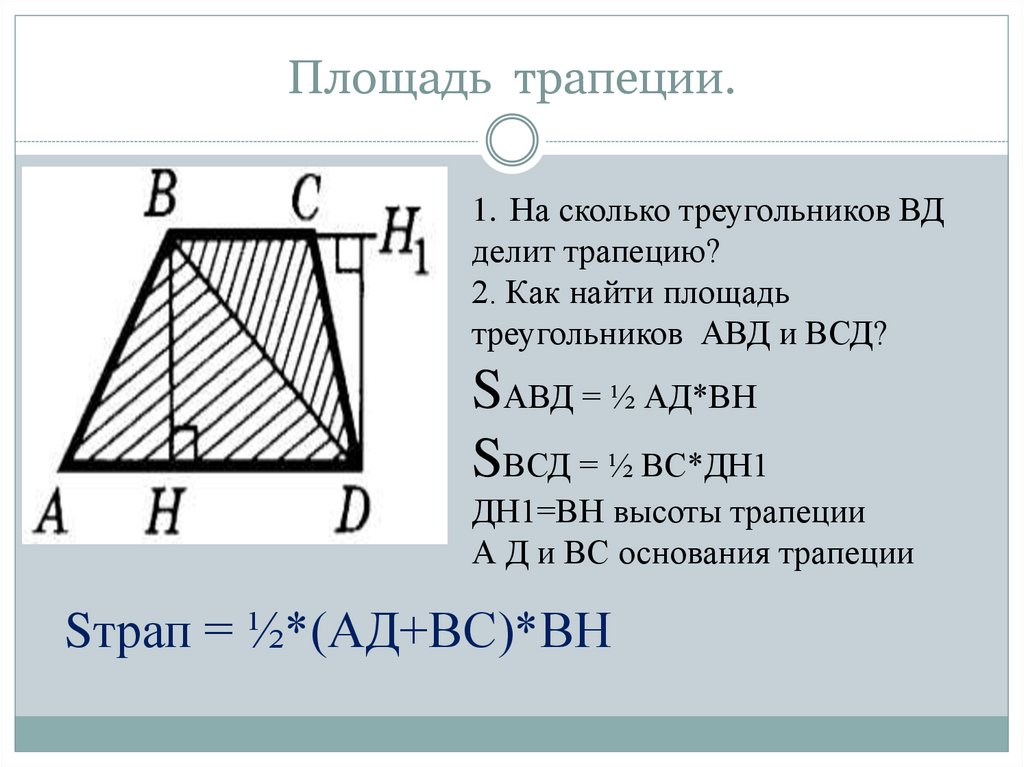
49. Площадь трапеции.
1. На сколько треугольников ВДделит трапецию?
2. Как найти площадь
треугольников АВД и ВСД?
SАВД = ½ АД*ВН
SВСД = ½ ВС*ДН1
ДН1=ВН высоты трапеции
А Д и ВС основания трапеции
Sтрап = ½*(АД+ВС)*ВН
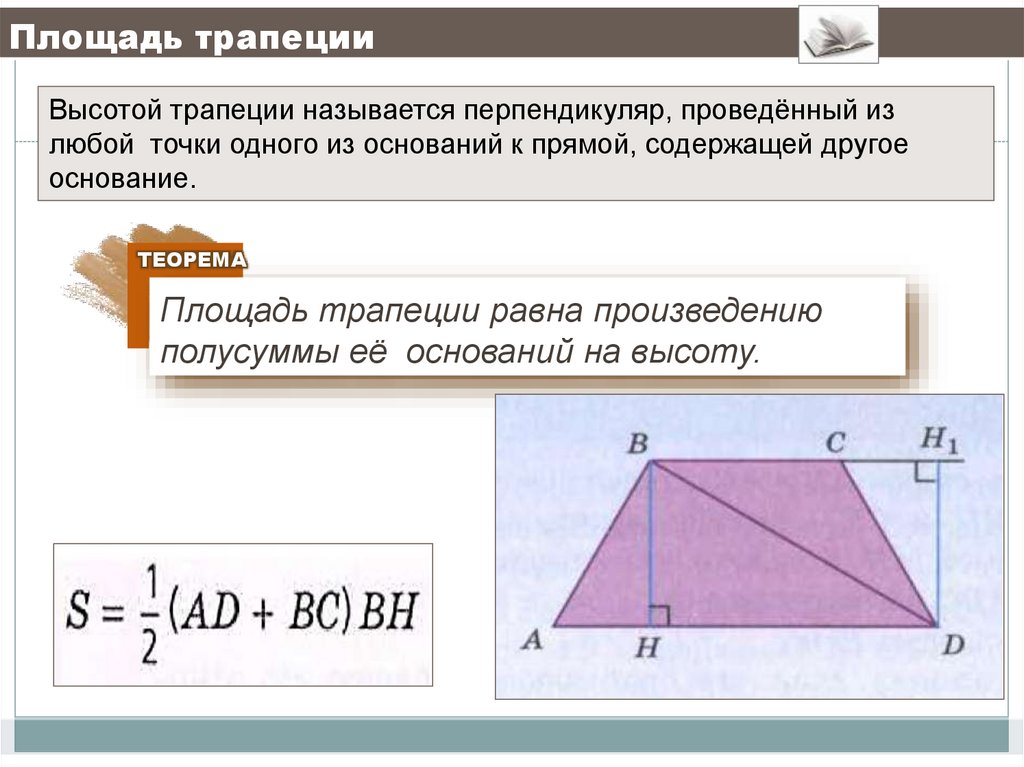
50. Площадь трапеции
Высотой трапеции называется перпендикуляр, проведённый излюбой точки одного из оснований к прямой, содержащей другое
основание.
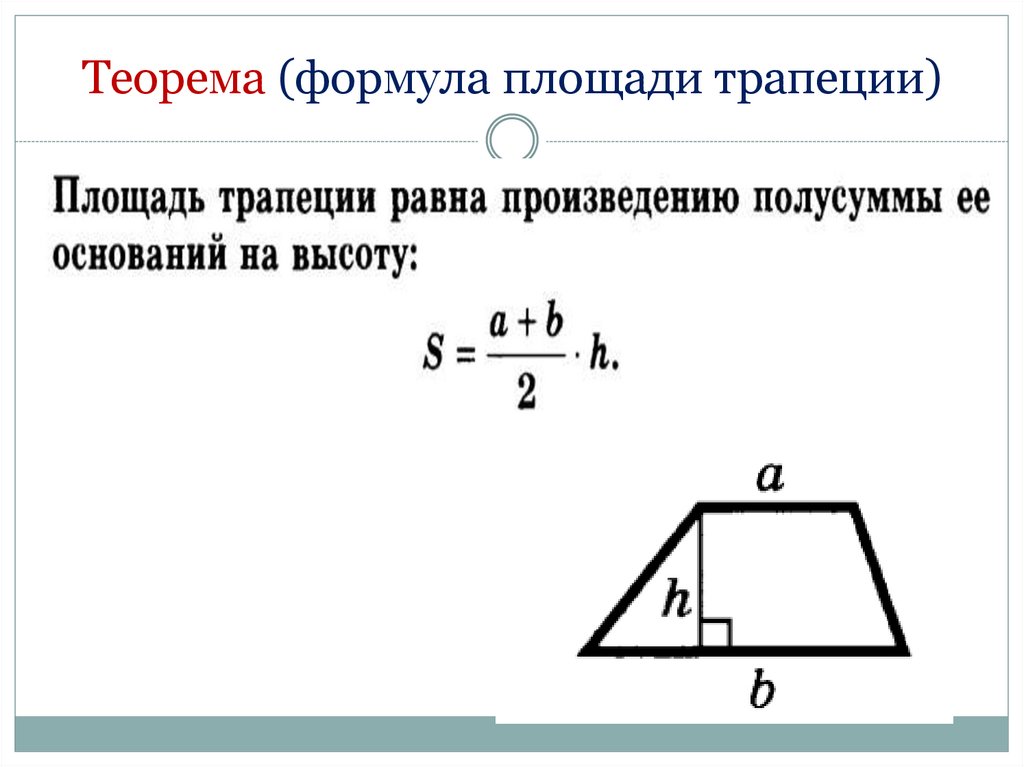
ТЕОРЕМА
Площадь трапеции равна произведению
полусуммы её оснований на высоту.
51. Теорема (формула площади трапеции)
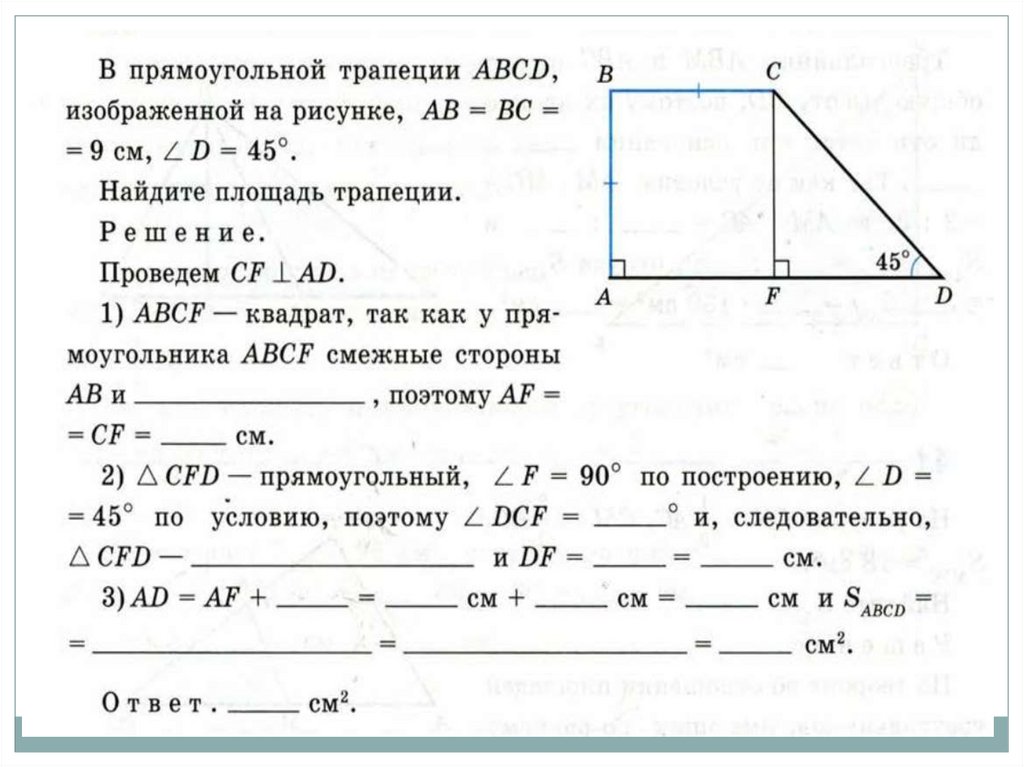
52.
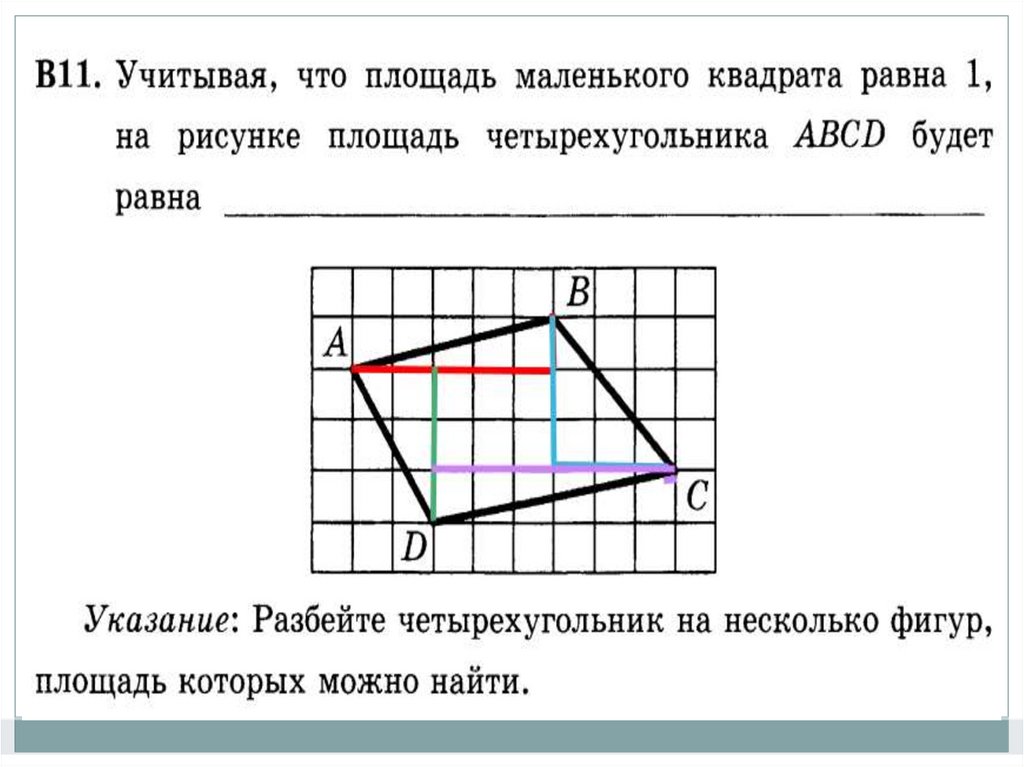
53.
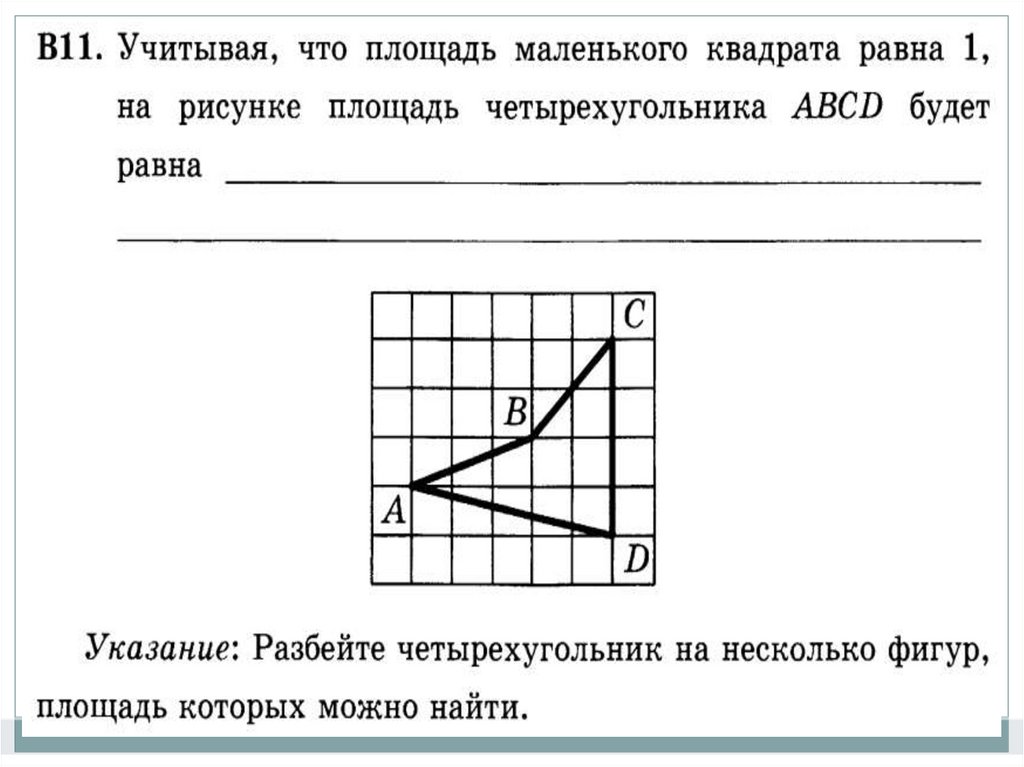
54.
55.
56.
57.
58. Притча
Шел мудрец, а навстречу ему три человека, которыевезли под горячим солнцем тележки с камнями для
строительства. Мудрец остановился и задал каждому по
вопросу. У первого спросил: “Что ты делал целый день?”
И тот с ухмылкой ответил, что целый день возил
проклятые камни. У второго мудрец спросил: “А что ты
делал целый день?”, и тот ответил: “А я добросовестно
выполнял свою работу”. А третий улыбнулся, его лицо
засветилось радостью и удовольствием: “А я принимал
участие в строительстве храма”
– Кто работал так, как первый человек?
– Кто работал добросовестно?
– Кто принимал участие в строительстве храма
знаний?
59. Итоги…
1. Какие у вас былизатруднения на уроке?
2. Нашли ли вы выход из
затруднения?
3. Остались ли у вас
затруднения после
окончания урока?
4. Над чем необходимо
продолжить работу?





























 mathematics
mathematics








