Повторение планиметрии

1. Презентация к открытому уроку «Повторение планиметрии»

ГБОУ Дудинская ВСШ
Учитель: Серебрянская Л.А.

2. Повторение теории ответы к тесту

1)Трапеция
2)Параллелограмм
3)Прямоугольник
4)Ромб
5)Квадрат
6)Хорда
7)Диаметр
8)Радиус
9)Медиана
10) Прямой
11) Периметр
12)Равнобедренный
13)Прямоугольная
14)Гипотенуза
15)Центральный

3.

Название плоских
фигур
1.
Квадрат
2.
Прямоугольник
3.
Трапеция
4.
Параллелограмм
5
Ромб
6.
Треугольник
7.
Круг
Формулы для
вычисления
площади
плоских фигур
Плоские фигуры

4. Квадрат

Площадь квадрата равна квадрату его стороны

5. Прямоугольник

Площадь прямоугольника равна произведению
его смежных сторон

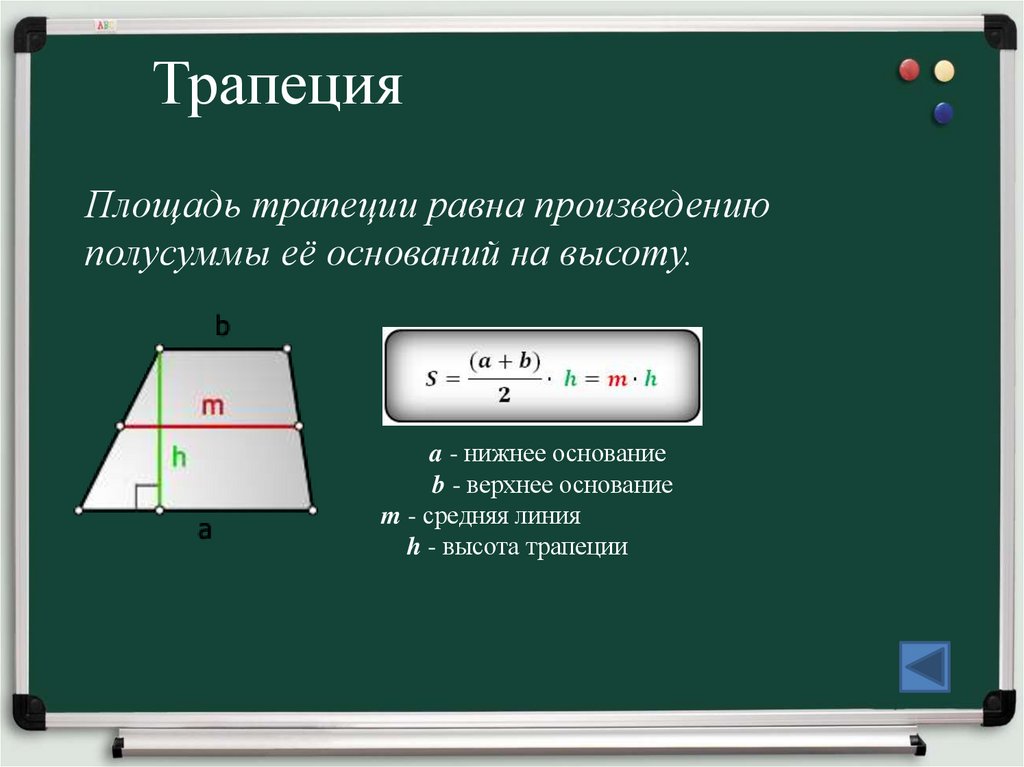
6. Трапеция

Площадь трапеции равна произведению
полусуммы её оснований на высоту.
a - нижнее основание
b - верхнее основание
m - средняя линия
h - высота трапеции

7. Параллелограмм

Площадь параллелограмма равна
произведению его основания на высоту.

8. Ромб

Площадь ромба равна половине произведения
его диагоналей.

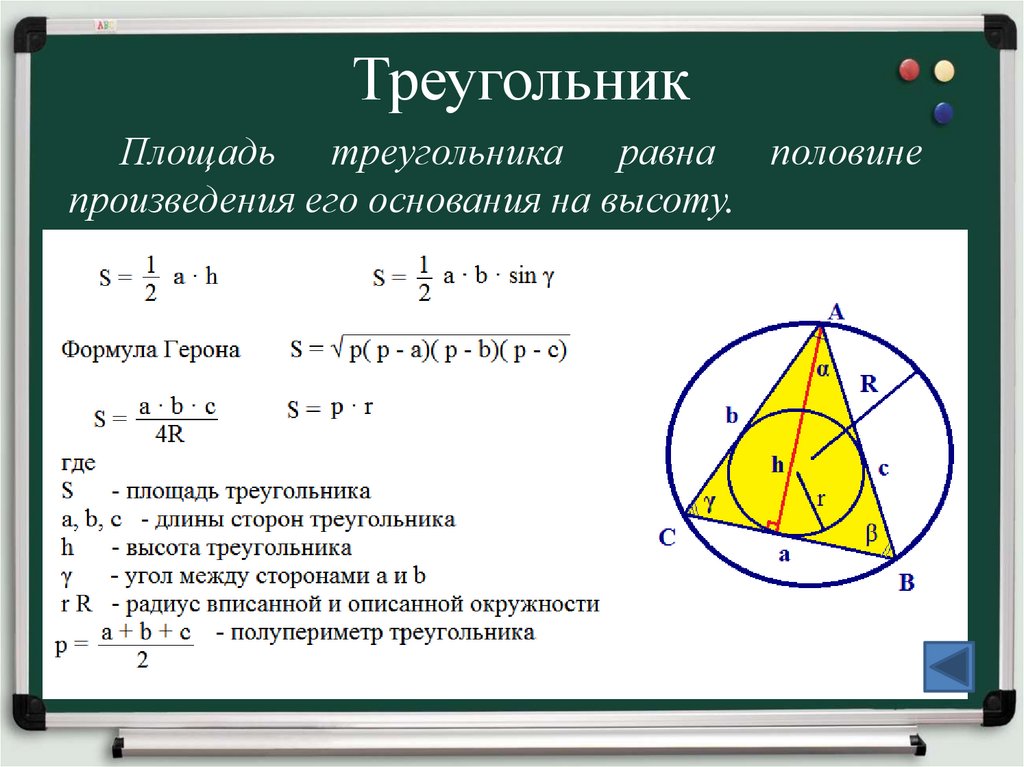
9. Треугольник

Площадь треугольника равна половине
произведения его основания на высоту.

10. Круг

Площадь круга равна произведению квадрата радиуса
на число пи (3.1415).

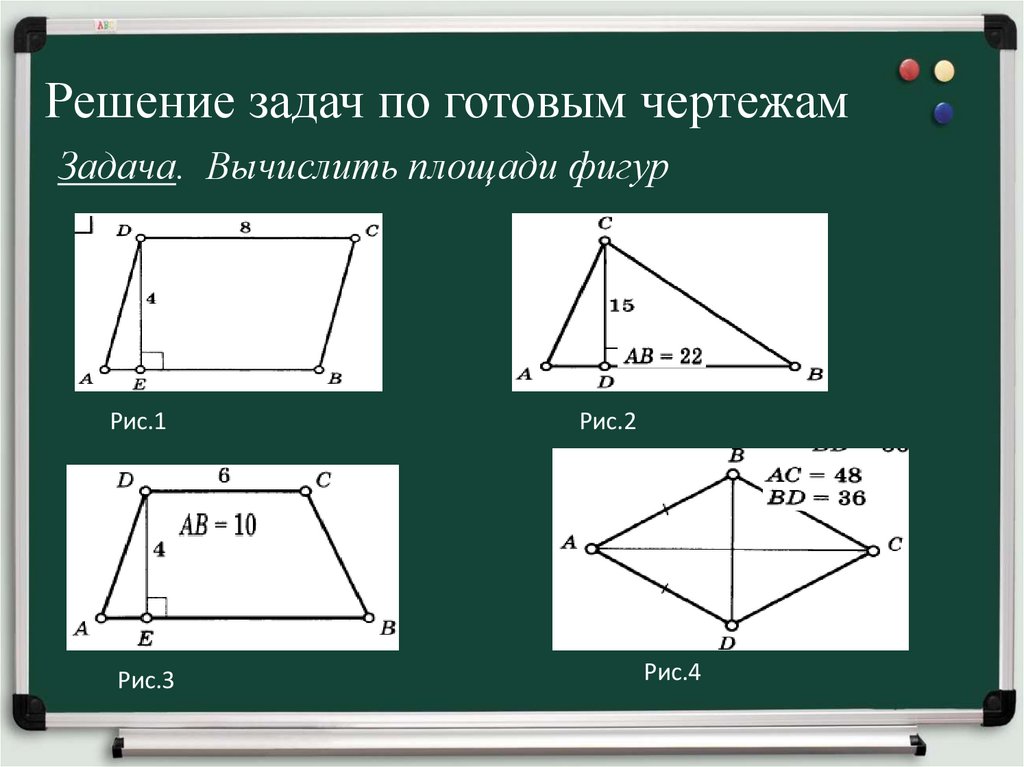
11. Решение задач по готовым чертежам Задача. Вычислить площади фигур

Рис.1
Рис.3
Рис.2
Рис.4

12. Задача. В прямоугольной трапеции основания равны 6 см и 9 см, а большая боковая сторона равна 5 см. Найдите площадь этой

трапеции.
Дано: ABCD – прямоугольная трапеция
А – прямой, ВС, AD – основания
ВС = 6 см ,АD = 9 см, СD = 5 см
Найти: SABCD - ?
Решение:
1) ABCD – прямоугольная трапеция, BC, AD – основания, А – прямой
AB AD CD – большая боковая сторона.
2) проведём __________СН СН AD СНD – _____________
АВСН – _________________
(ВС АН, АВ АН, СН АН).
3) АВСН – ________________ ВС = АН = 6 см, HD = AD – AH = 9 – 6 = 3 (см).
4) в _______________ СНD по теореме Пифагора:

13. Теорема Пифагора

В прямоугольном треугольнике квадрат длины
гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы
треугольника через c, а длины катетов через a и b:

14. Интернет ресурсы:

• http://www-formula.ru/index.php/