Планиметрия. Материалы ЕГЭ и Г(И)А. 2013 - 2014 год

1.

материалы ЕГЭ и Г(И)А
2013 - 2014г.

2.

ПОЯСНИТЕЛЬНАЯ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ЗАПИСКА
Геометрия
Геометрия является
является одним
одним из
из центральных
центральных разделов
разделов школьной
школьной
математики.
математики. Но
Но по
по ряду
ряду причин
причин иногда
иногда изучение
изучение именно
именно этого
этого раздела
раздела
вызывает
вызывает уу учащихся
учащихся затруднения.
затруднения.
Геометрия
Геометрия –
– наиболее
наиболее уязвимое
уязвимое звено
звено школьной
школьной математики.
математики.
Задания
Задания частей
частей В
Ви
иС
С единого
единого государственного
государственного экзамена
экзамена содержат
содержат
задания
задания по
по геометрии,
геометрии, в
в том
том числе
числе и
и из
из планиметрии.
планиметрии. Итоги
Итоги предыдущих
предыдущих лет
лет
показали,
показали, что
что учащиеся
учащиеся сс данными
данными заданиями
заданиями справлялись
справлялись хуже,
хуже, а
а иногда
иногда
даже
даже не
не выполняли
выполняли их,
их, что
что связано
связано сс малым
малым опытом
опытом решения
решения геометрических
геометрических
задач.
задач. Одно
Одно из
из назначений
назначений данной
данной презентации
презентации восполнить
восполнить этот
этот пробел.
пробел.
Все
Все задачи
задачи взяты
взяты из
из открытого
открытого банка
банка задач:
задач: http://mathege.ru/
http://mathege.ru/

3. содержание

треугольник
параллелограмм
прямоугольник, ромб, квадрат
трапеция
вписанная окружность и описанная
окружность
• площади

4.

Задача:
Гипотенуза прямоугольного треугольника равна 26.
Один из его катетов равен 10. Найдите другой катет.
Решение:
∆ ABС – прямоугольный.
АВ = 26; ВС =10.
по теореме Пифагора:
Ответ: 24
содержание

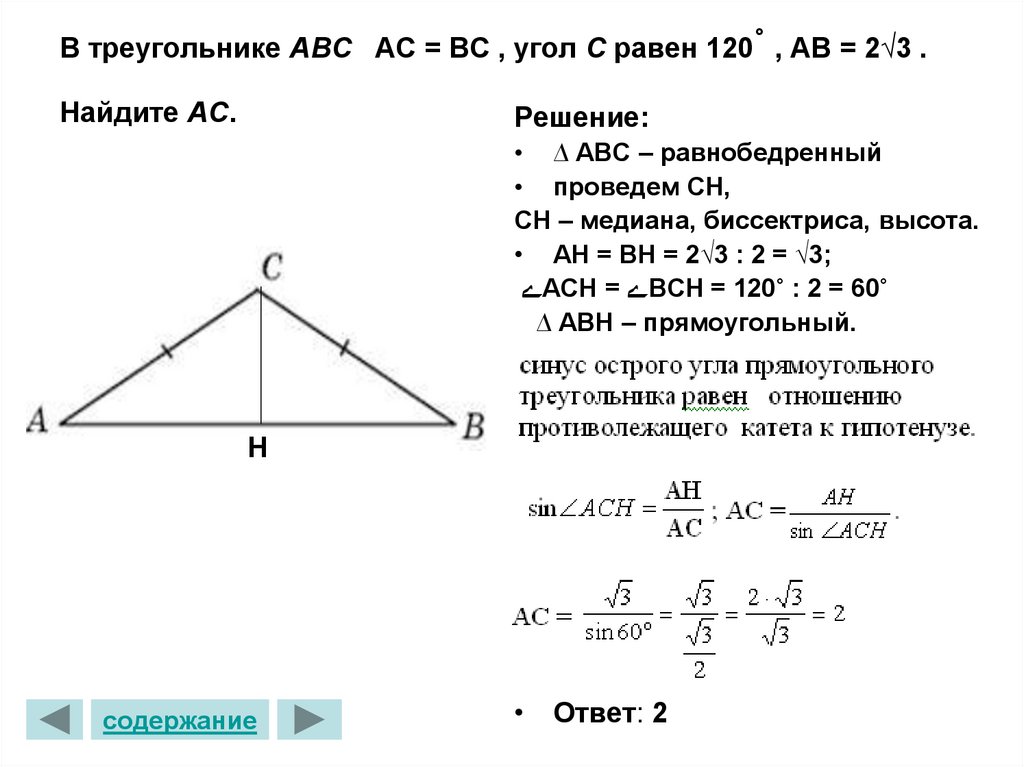
5. В треугольнике ABC  АС = ВС , угол C равен 120˚ , АВ = 2√3 . Найдите AC.

В треугольнике ABC АС = ВС , угол C равен 120˚ , АВ = 2√3 .
Найдите AC.
Решение:
• ∆ ABС – равнобедренный
• проведем СН,
СН – медиана, биссектриса, высота.
• АН = ВН = 2√3 : 2 = √3;
‫ے‬AСН = ‫ے‬BСН = 120˚ : 2 = 60˚
∆ ABН – прямоугольный.
Н
содержание
• Ответ: 2

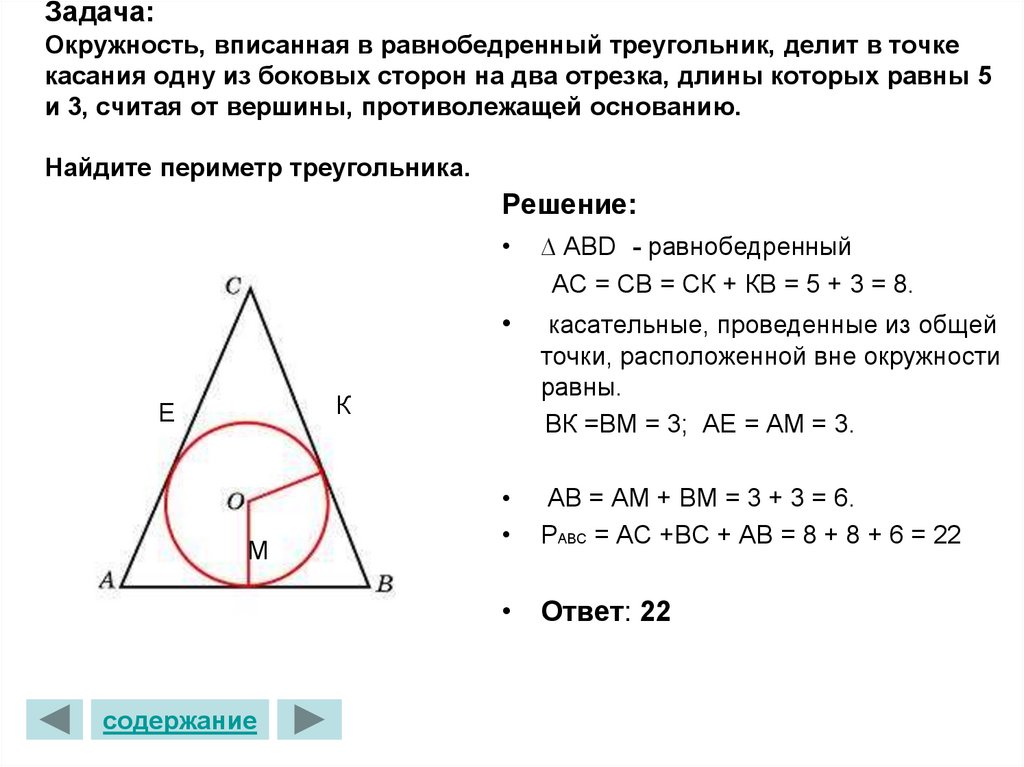
6. Задача: Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины

которых равны 5
и 3, считая от вершины, противолежащей основанию.
Найдите периметр треугольника.
Решение:
∆ ABD - равнобедренный
АС = СВ = СК + КВ = 5 + 3 = 8.
касательные, проведенные из общей
точки, расположенной вне окружности
равны.
ВК =ВМ = 3; АЕ = АМ = 3.
AB = АМ + ВМ = 3 + 3 = 6.
РАВС = АС +ВС + АВ = 8 + 8 + 6 = 22
К
Е
М
• Ответ: 22
содержание

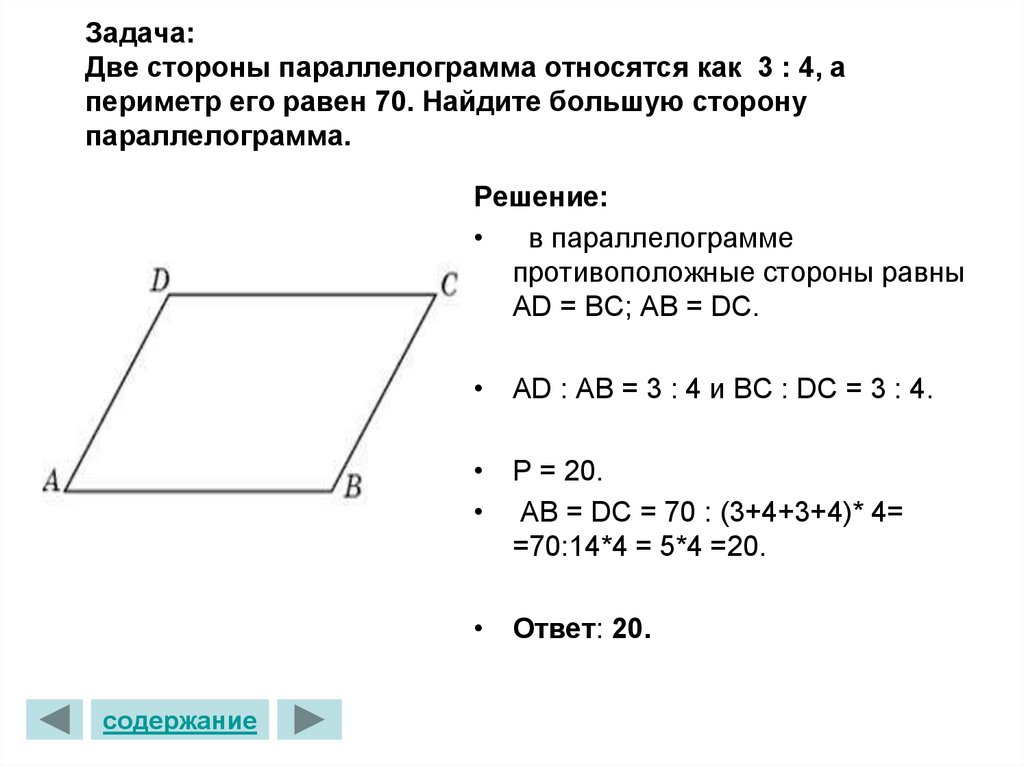
7. Задача: Две стороны параллелограмма относятся как  3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.

Задача:
Две стороны параллелограмма относятся как 3 : 4, а
периметр его равен 70. Найдите большую сторону
параллелограмма.
Решение:
в параллелограмме
противоположные стороны равны
АD = BC; AB = DC.
• AD : AB = 3 : 4 и BC : DC = 3 : 4.
• Р = 20.
• AB = DC = 70 : (3+4+3+4)* 4=
=70:14*4 = 5*4 =20.
• Ответ: 20.
содержание

8. Задача: Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого

Задача:
Биссектриса тупого угла параллелограмма делит противоположную
сторону в отношении 4 : 3, считая от вершины острого угла. Найдите
большую сторону параллелограмма, если его периметр равен 88.
К
содержание
Решение:
по условию АК : ВК = 4 : 3.
биссектриса параллелограмма
отсекает равнобедренный
треугольник.
АВК – равнобедренный;
AD = AK.
• AD : АВ = 4 :7.
• РABCD = 88.
• АВ = DC = 88 : (4+7+4+7)*7 =
= 88 : 22*7 = 4*7 = 28
Ответ: 28

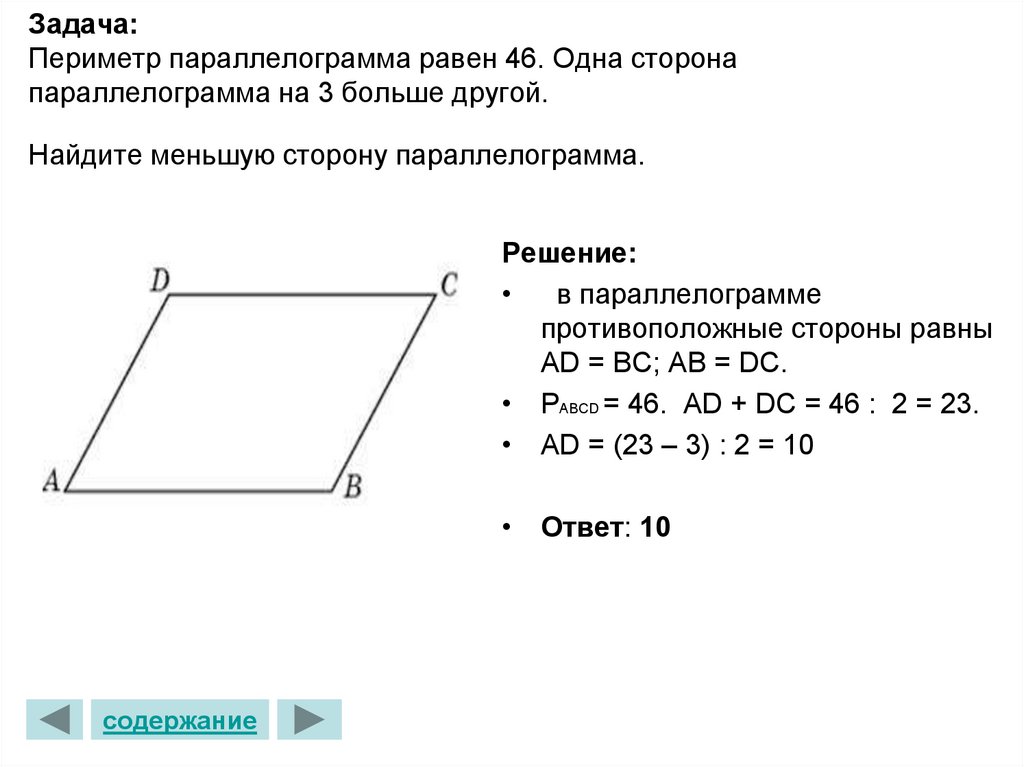
9. Задача: Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону

параллелограмма.
Решение:
в параллелограмме
противоположные стороны равны
АD = BC; AB = DC.
• РABCD = 46. AD + DC = 46 : 2 = 23.
• AD = (23 – 3) : 2 = 10
• Ответ: 10
содержание

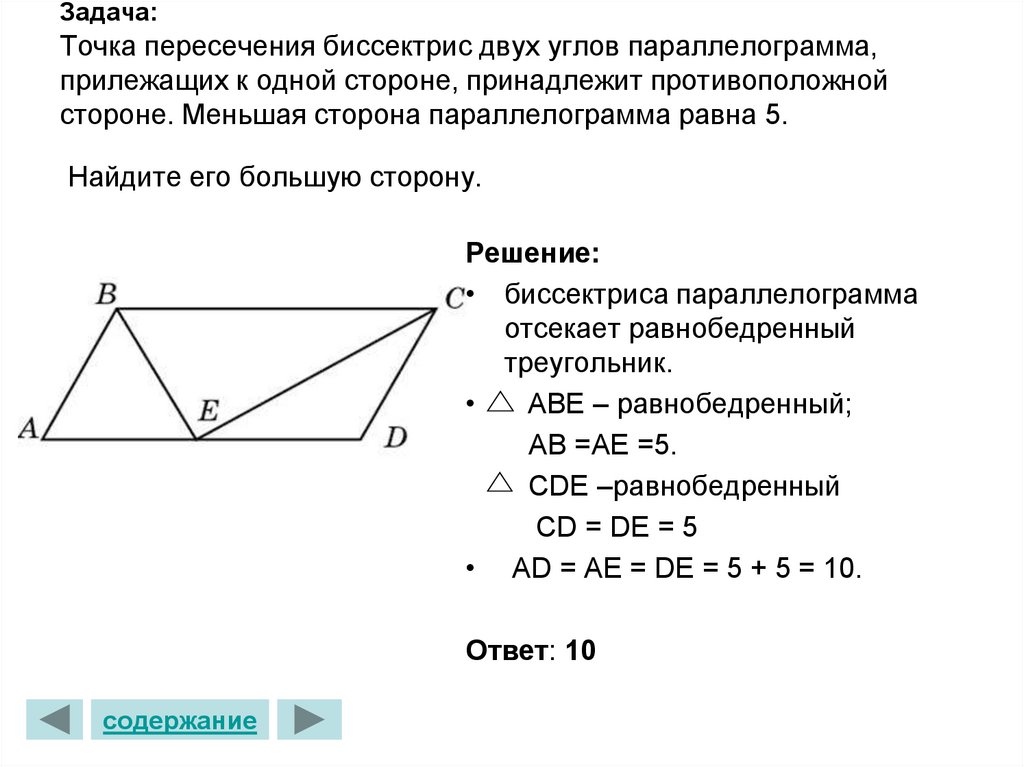
10. Задача: Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной

стороне. Меньшая сторона параллелограмма равна 5.
Найдите его большую сторону.
Решение:
• биссектриса параллелограмма
отсекает равнобедренный
треугольник.
АВЕ – равнобедренный;
АВ =АЕ =5.
СDE –равнобедренный
CD = DE = 5
• AD = AE = DE = 5 + 5 = 10.
Ответ: 10
содержание

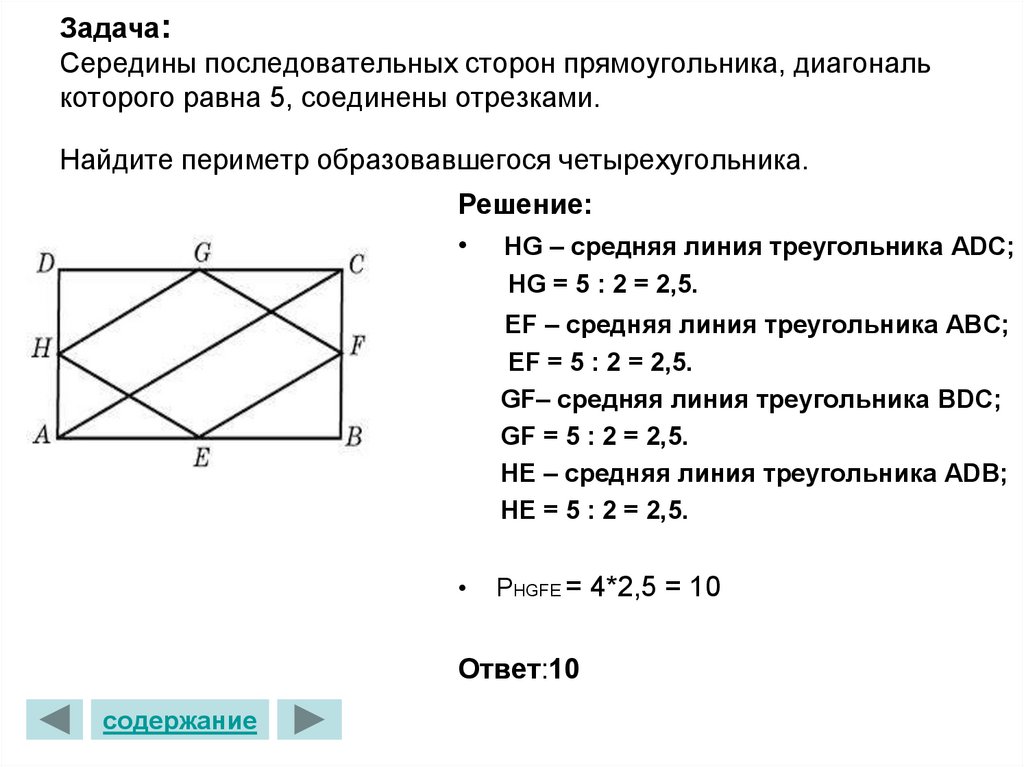
11. Задача: Середины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр

образовавшегося четырехугольника.
Решение:
• HG – средняя линия треугольника ADC;
HG = 5 : 2 = 2,5.
EF – средняя линия треугольника ABC;
EF = 5 : 2 = 2,5.
GF– средняя линия треугольника BDC;
GF = 5 : 2 = 2,5.
HE – средняя линия треугольника ADB;
HE = 5 : 2 = 2,5.
PHGFE = 4*2,5 = 10
Ответ:10
содержание

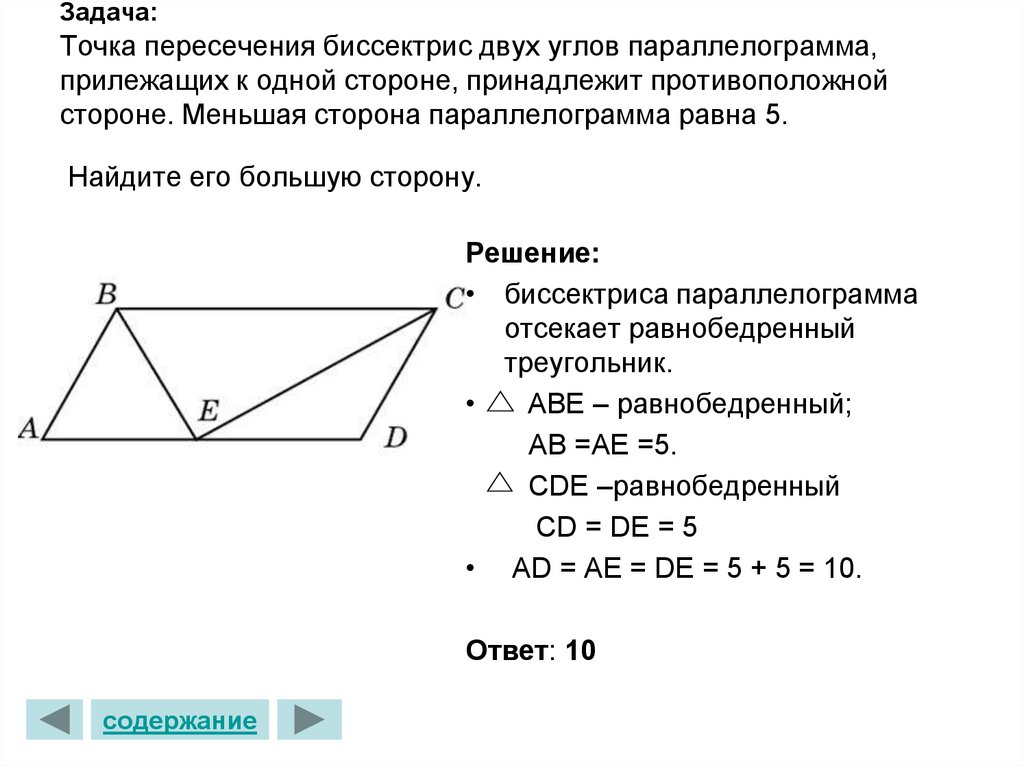
12. Задача: Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной

стороне. Меньшая сторона параллелограмма равна 5.
Найдите его большую сторону.
Решение:
• биссектриса параллелограмма
отсекает равнобедренный
треугольник.
АВЕ – равнобедренный;
АВ =АЕ =5.
СDE –равнобедренный
CD = DE = 5
• AD = AE = DE = 5 + 5 = 10.
Ответ: 10
содержание

13. Задача: Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ

разделила прямоугольник, равен 24
Решение:
• у прямоугольника
противоположные стороны равны
АD = BC; AB = DC.
• РABCD = 28;
AD + DC = 28 : 2 = 14.
• PABC =24.
AD + DC + AC = 24.
• AC = PABC – (AD + DC) = 24 -14 =10.
• Ответ: 10
содержание

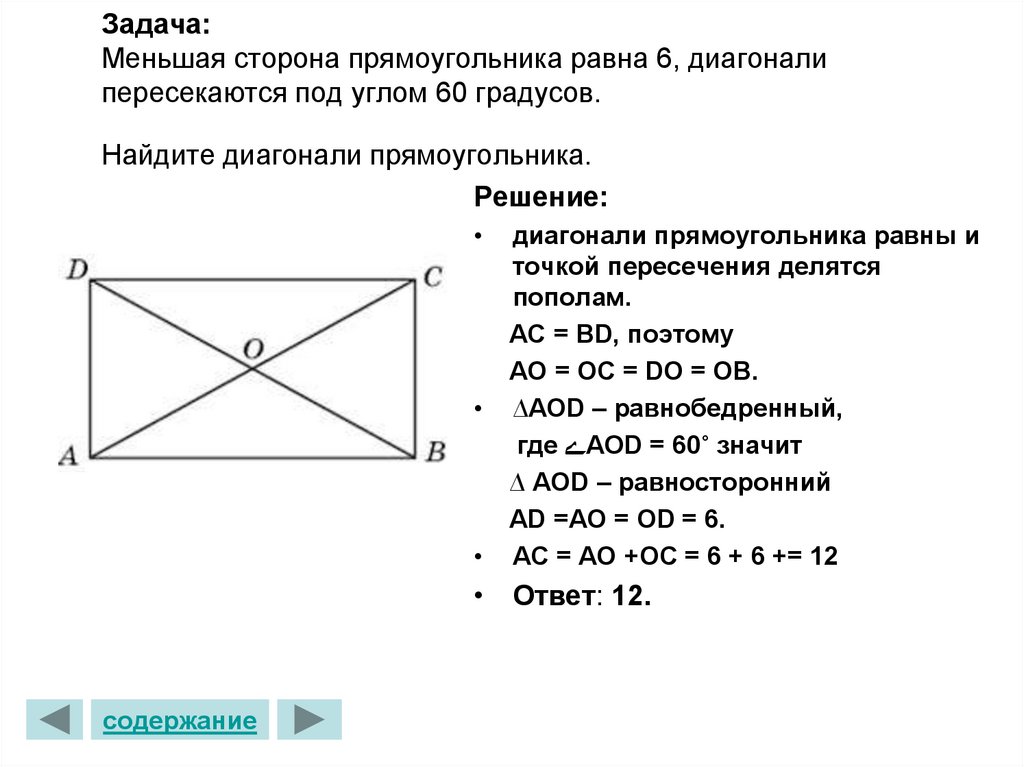
14. Задача: Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 60 градусов. Найдите диагонали прямоугольника.

Задача:
Меньшая сторона прямоугольника равна 6, диагонали
пересекаются под углом 60 градусов.
Найдите диагонали прямоугольника.
Решение:
диагонали прямоугольника равны и
точкой пересечения делятся
пополам.
AC = BD, поэтому
AO = OC = DO = OB.
∆АОD – равнобедренный,
где ‫ے‬АОD = 60˚ значит
∆ АОD – равносторонний
АD =AO = OD = 6.
AC = AO +OC = 6 + 6 += 12
• Ответ: 12.
содержание

15. . Задача: В прямоугольнике диагональ делит угол в отношении  1 : 2, меньшая его сторона равна 6. Найдите диагональ данного

.
Задача:
В прямоугольнике диагональ делит угол в отношении 1 : 2,
меньшая его сторона равна 6. Найдите диагональ данного
прямоугольника
Решение:
• ∆ ABD – прямоугольный.
‫ے‬BAС + ‫ے‬AСD = 90˚.
‫ ے‬BAС : ‫ے‬AСD = 2 : 1.
‫ ے‬BAС = 90˚ :3 = 30˚
• катет, лежащий против угла в 30˚ равен
половине гипотенузы.
ВС = АС : 2. АС = 2* ВС = 2*6 =12.
Ответ: 12.
содержание

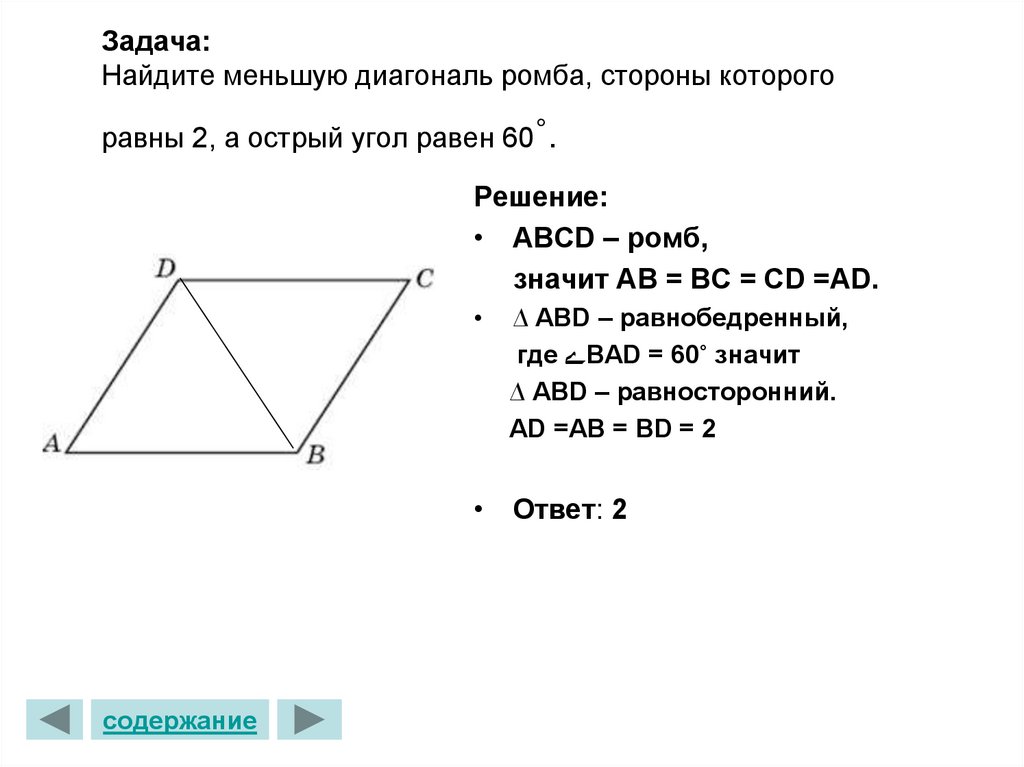
16. Задача: Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен 60˚.

Решение:
• ABCD – ромб,
значит AB = BC = CD =AD.
∆ ABD – равнобедренный,
где ‫ے‬BAD = 60˚ значит
∆ АBD – равносторонний.
AD =AB = BD = 2
• Ответ: 2
содержание

17. Задача: Найдите высоту ромба, сторона которого равна √3 , а острый угол равен 60˚.

Задача: Найдите высоту ромба, сторона которого равна √3
, а острый угол равен 60˚.
содержание

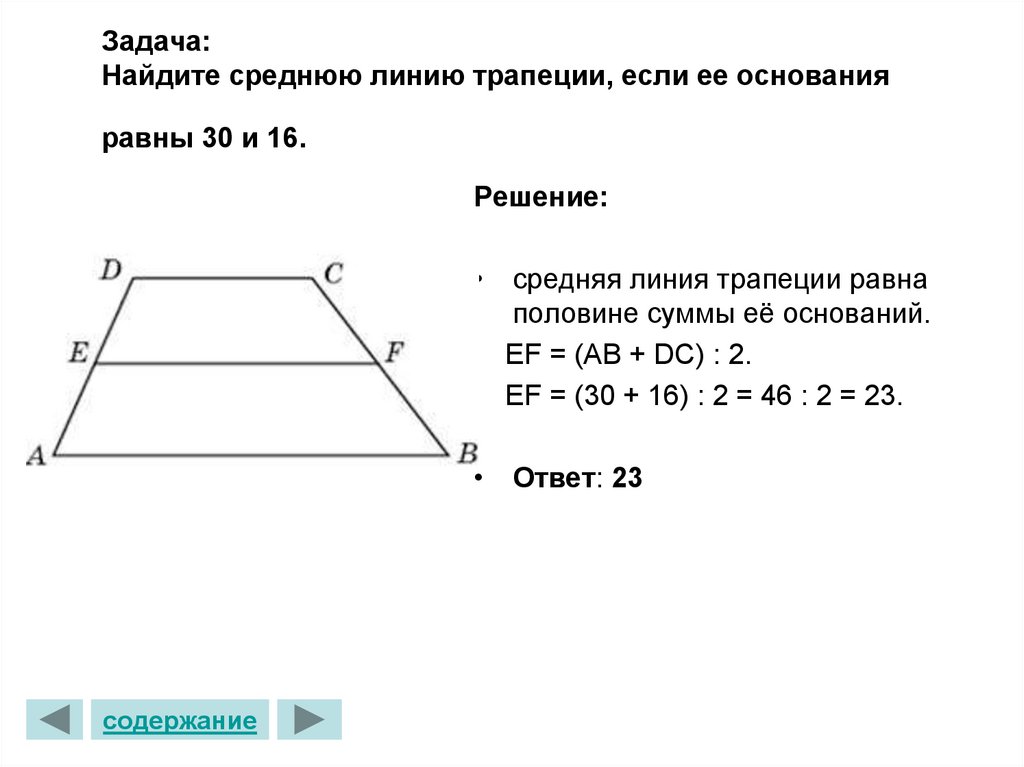
18. Задача: Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Решение:
• средняя линия трапеции равна
половине суммы её оснований.
ЕF = (AB + DC) : 2.
ЕF = (30 + 16) : 2 = 46 : 2 = 23.
• Ответ: 23
содержание

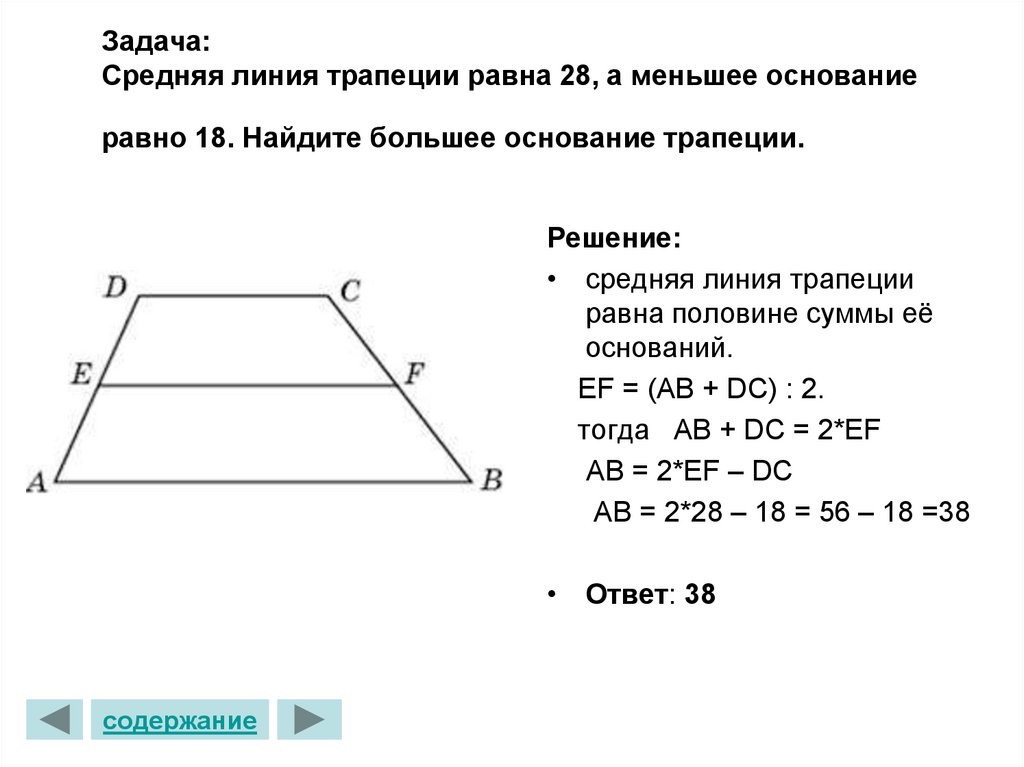
19. Задача: Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Решение:
• средняя линия трапеции
равна половине суммы её
оснований.
ЕF = (AB + DC) : 2.
тогда AB + DC = 2*EF
AB = 2*EF – DC
AB = 2*28 – 18 = 56 – 18 =38
• Ответ: 38
содержание

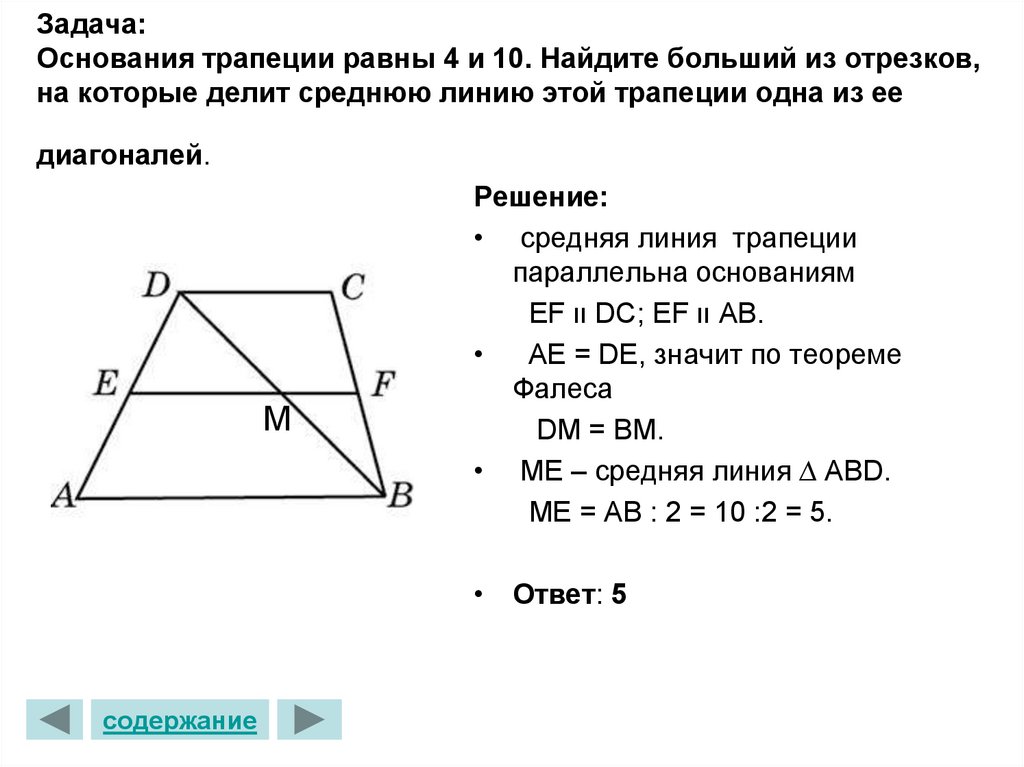
20. Задача: Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее

диагоналей.
M
Решение:
• средняя линия трапеции
параллельна основаниям
EF ‫ װ‬DC; EF ‫ װ‬AB.
AE = DE, значит по теореме
Фалеса
DM = BM.
• ME – средняя линия ∆ ABD.
ME = AB : 2 = 10 :2 = 5.
• Ответ: 5
содержание

21. Задача: Около окружности, радиус которой равен √8, описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

Задача:
Около окружности, радиус которой равен √8, описан
квадрат. Найдите радиус окружности, описанной около
этого квадрата.
О
содержание
М

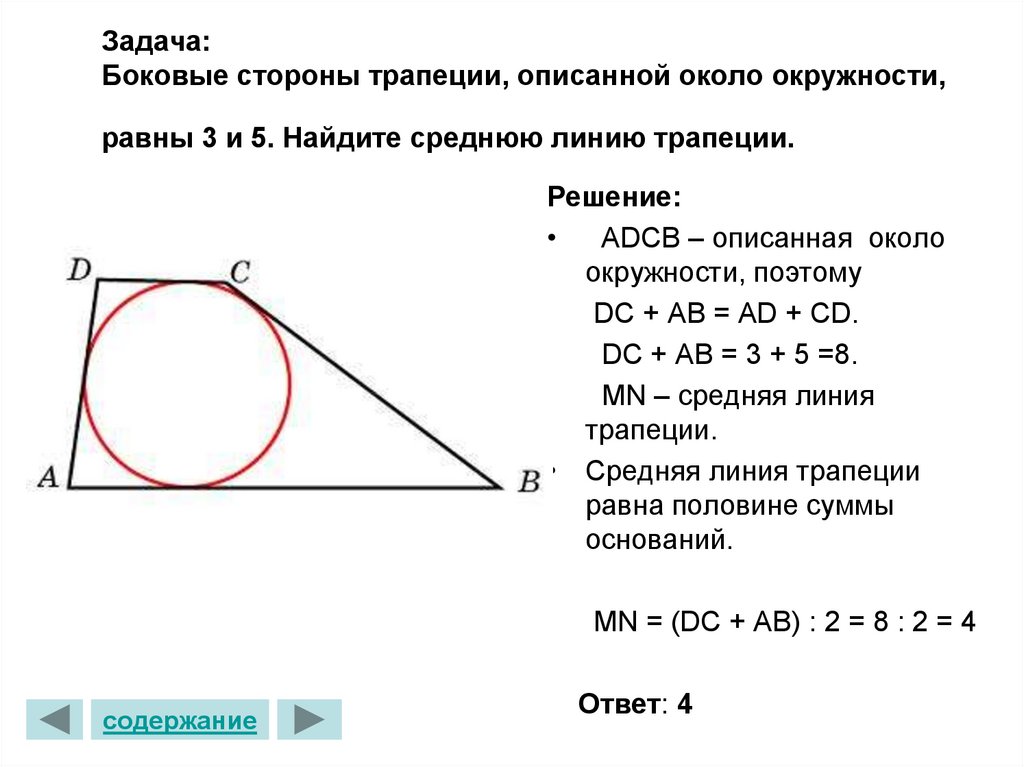
22. Задача: Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

Решение:
АDCB – описанная около
окружности, поэтому
DC + AB = AD + CD.
DC + AB = 3 + 5 =8.
MN – средняя линия
трапеции.
• Средняя линия трапеции
равна половине суммы
оснований.
MN = (DC + AB) : 2 = 8 : 2 = 4
содержание
Ответ: 4

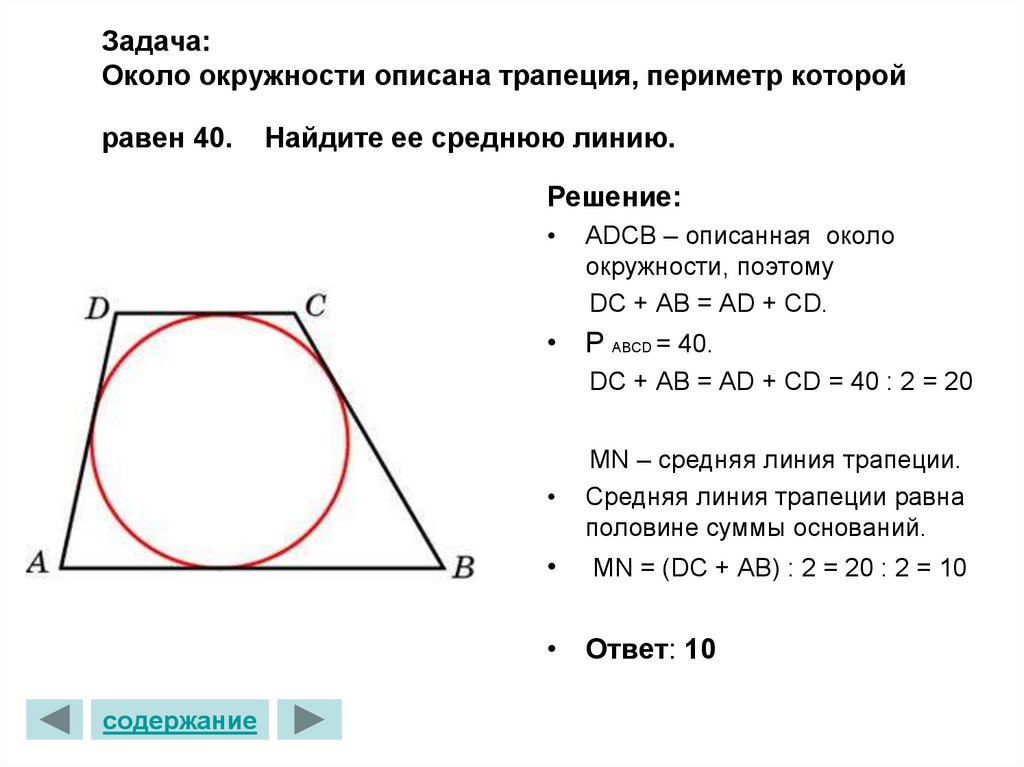
23. Задача: Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Решение:
АDCB – описанная около
окружности, поэтому
DC + AB = AD + CD.
• Р ABCD = 40.
DC + AB = AD + CD = 40 : 2 = 20
MN – средняя линия трапеции.
Средняя линия трапеции равна
половине суммы оснований.
MN = (DC + AB) : 2 = 20 : 2 = 10
• Ответ: 10
содержание

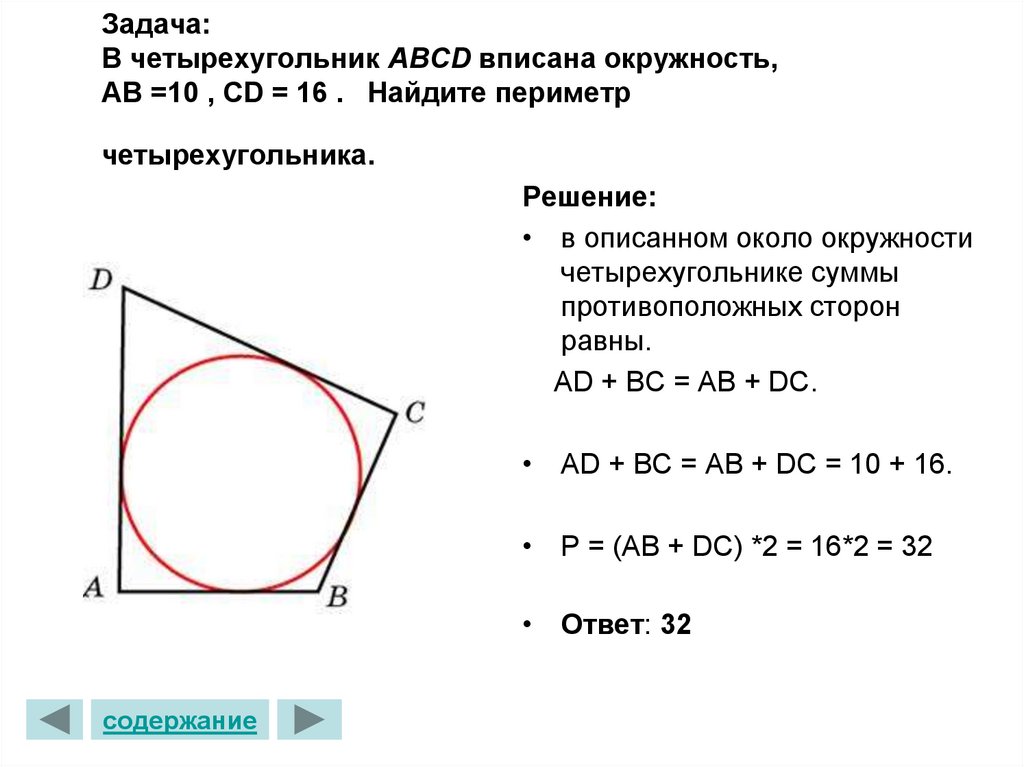
24. Задача: В четырехугольник ABCD вписана окружность,  АВ =10 , СD = 16 . Найдите периметр четырехугольника.   

Задача:
В четырехугольник ABCD вписана окружность,
АВ =10 , СD = 16 . Найдите периметр
четырехугольника.
Решение:
• в описанном около окружности
четырехугольнике суммы
противоположных сторон
равны.
АD + BC = AB + DC.
• АD + BC = AB + DC = 10 + 16.
• Р = (AB + DC) *2 = 16*2 = 32
• Ответ: 32
содержание

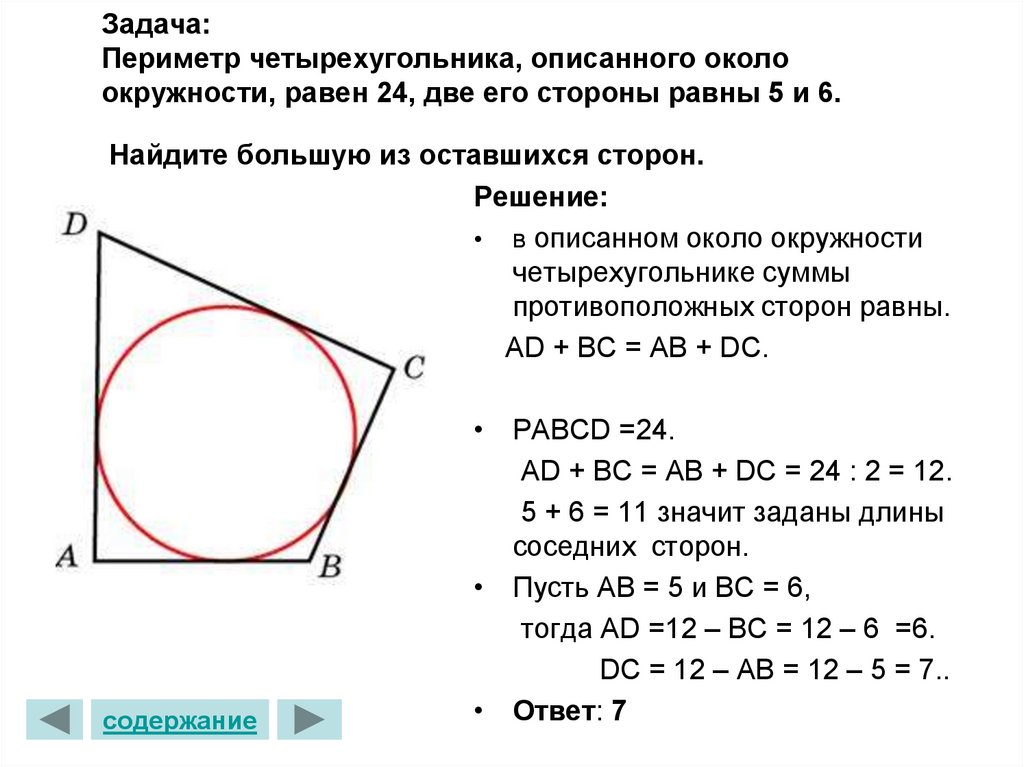
25. Задача: Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из

оставшихся сторон.
Решение:
• в описанном около окружности
четырехугольнике суммы
противоположных сторон равны.
АD + BC = AB + DC.
содержание
• РABCD =24.
АD + BC = AB + DC = 24 : 2 = 12.
5 + 6 = 11 значит заданы длины
соседних сторон.
• Пусть АВ = 5 и ВС = 6,
тогда АD =12 – BС = 12 – 6 =6.
DC = 12 – АВ = 12 – 5 = 7..
• Ответ: 7

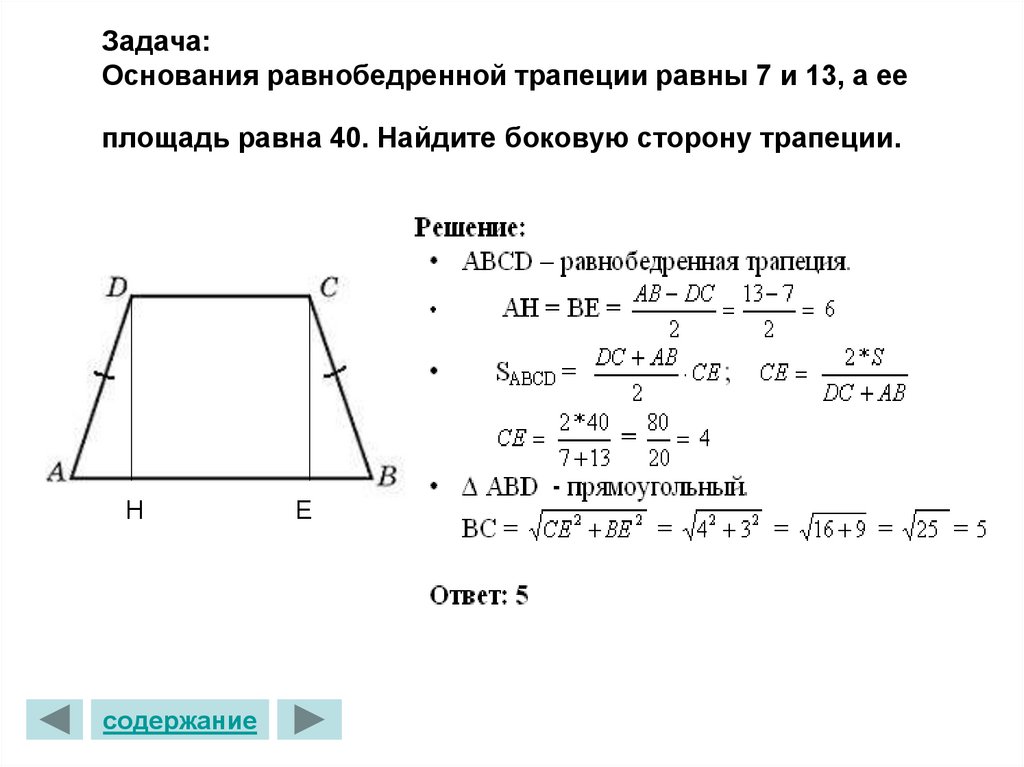
26. Задача: Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции. 

Задача:
Основания равнобедренной трапеции равны 7 и 13, а ее
площадь равна 40. Найдите боковую сторону трапеции.
Н
содержание
Е

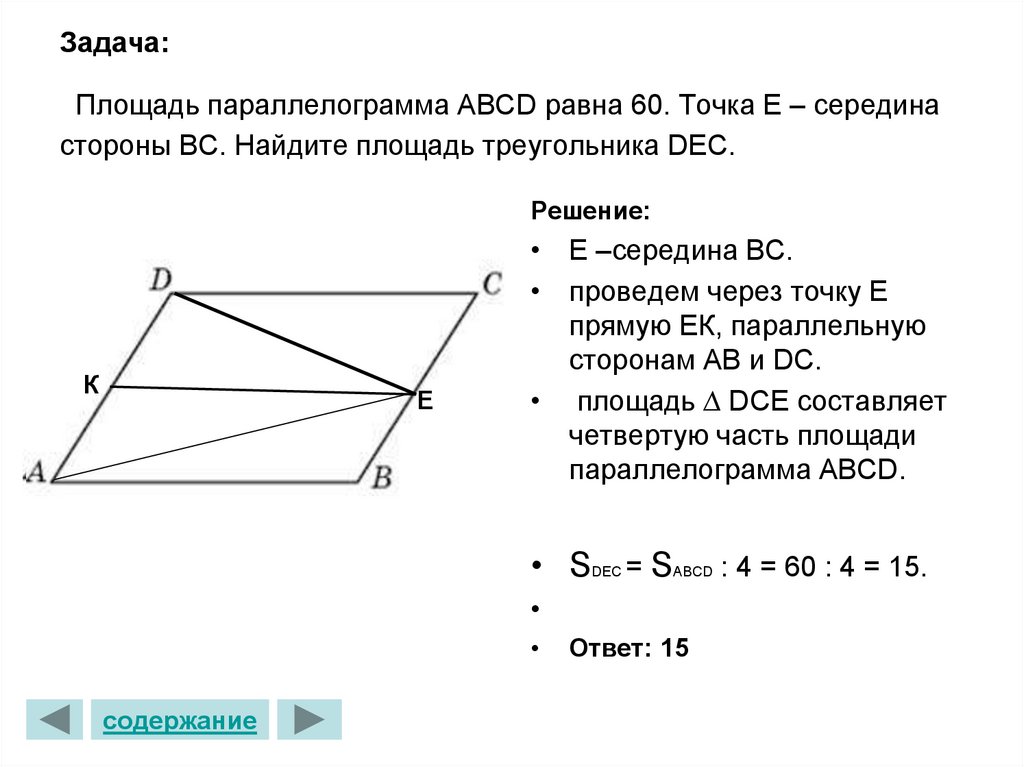
27. Задача: Площадь параллелограмма АВСD равна 60. Точка Е – середина стороны ВС. Найдите площадь треугольника DЕС.

Решение:
К
Е
Е
• Е –середина ВС.
• проведем через точку Е
прямую ЕК, параллельную
сторонам АВ и DС.
• площадь ∆ DСЕ составляет
четвертую часть площади
параллелограмма АВСD.
• SDEC = SABCD : 4 = 60 : 4 = 15.
содержание
Ответ: 15

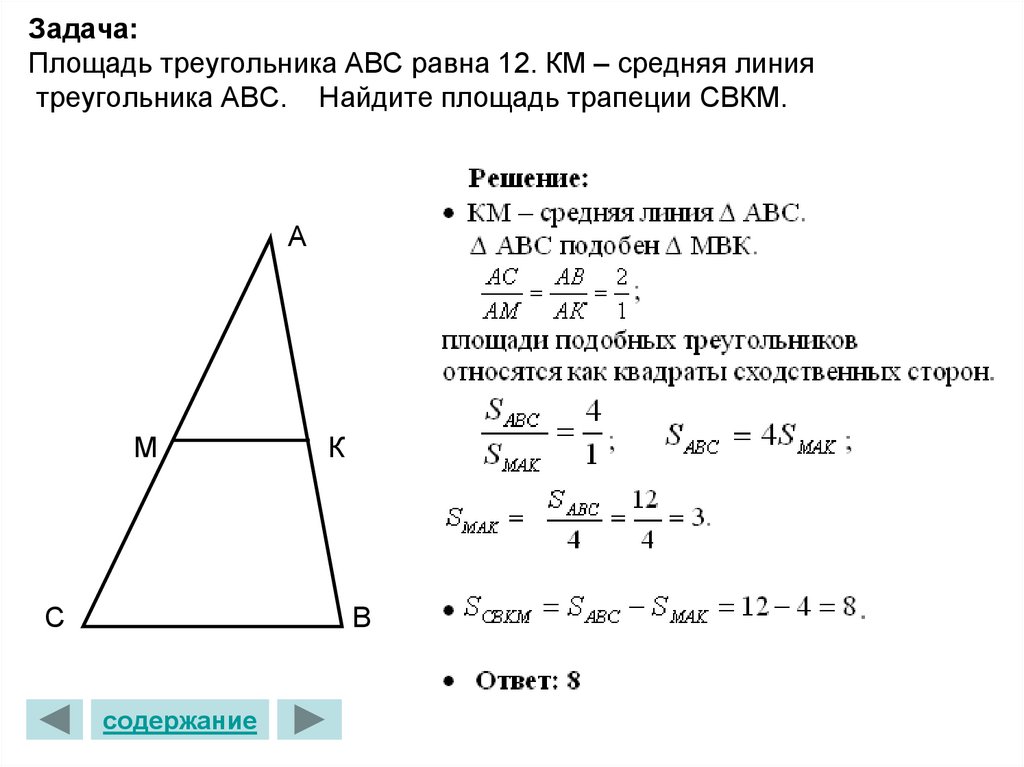
28. Задача: Площадь треугольника АВС равна 12. КМ – средняя линия треугольника АВС. Найдите площадь трапеции СВКМ.

А
М
С
К
В
содержание

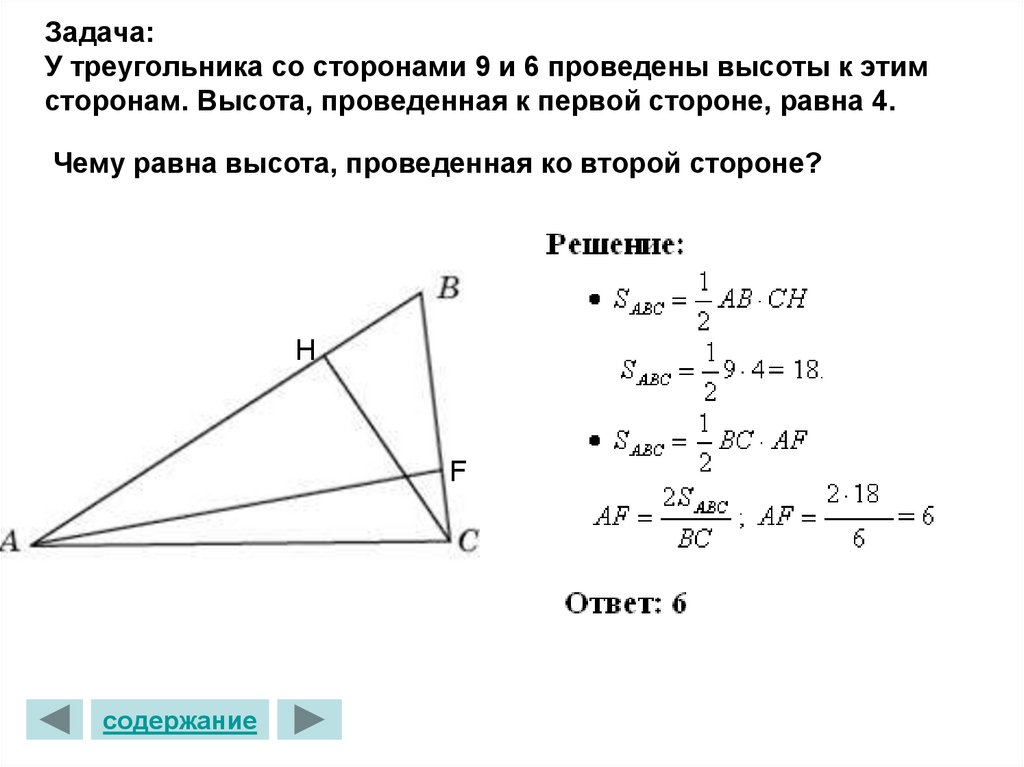
29. Задача: У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему

равна высота, проведенная ко второй стороне?
H
F
содержание