3сем_Лк 8_Системы ДУ

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
СИСТЕМЫ ОДНОРОДНЫХ
ДУ 1-ГО ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
22.12.2025
г. Санкт-Петербург
2025
1|13

2.

Содержание лекции
• Понятие системы линейных однородных ДУ 1-го порядка с
постоянными коэффициентами;
• Решение системы ДУ;
• Метод исключения (сведение системы ДУ к одному уравнению);
• Характеристическое уравнение системы;
• Система двух ДУ 1–го порядка.
2|13

3.

dx1
dt a11 x1 a12 x2 a1n xn ,
система ДУ с постоянными dx
2 a21 x1 a22 x2 a2 n xn ,
коэффициентами
dt
aij – постоянные (i, j 1, n)
dxn
t – аргумент
an1 x1 an 2 x2 ann xn ,
dt
x1 (t ), x2 (t ), …, xn (t ) – искомые функции
Линейная однородная
(1)
Решение системы (1) в интервале (a,b) - совокупность n функций xi i (t ),
(i 1, n), которые определены, непрерывно дифференцируемы в интервале
(a,b) и обращают все уравнения системы (1) в тождества.
Система из n линейно независимых частных решений системы (1)
называется ее фундаментальной системой решений
3|13

4.

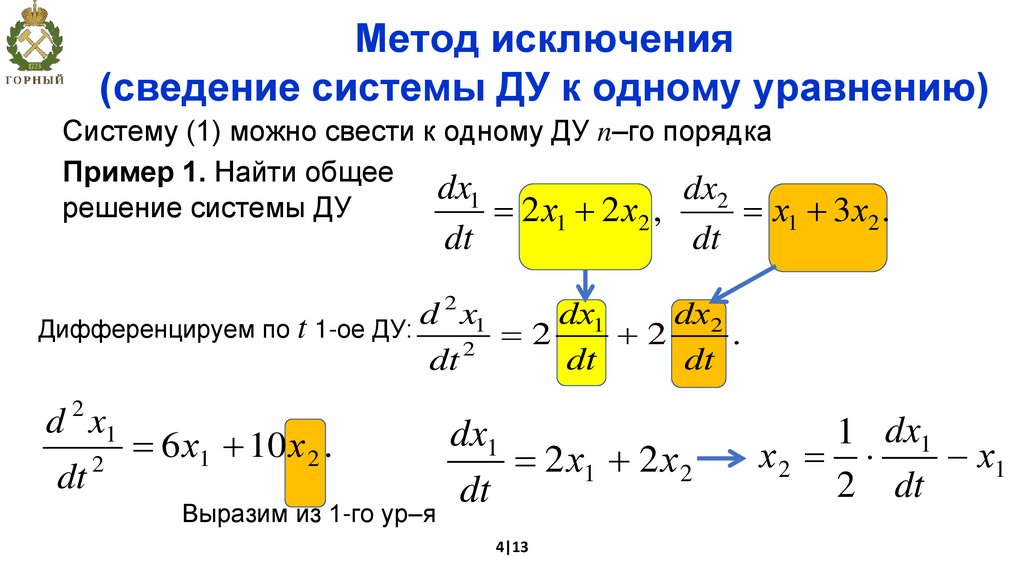
Метод исключения
(сведение системы ДУ к одному уравнению)
Систему (1) можно свести к одному ДУ n–го порядка
Пример 1. Найти общее
dx1
dx2
решение системы ДУ
2 х1 2 х2 ,
х1 3 х2 .
dt
dt
2
d
x
dх
dх
1
1
2
Дифференцируем по t 1-ое ДУ:
2
2
.
2
dt
dt
dt
2
d x1
dt
2
6 х1 10 х 2 .
Выразим из 1-го ур–я
dx1
2 х1 2 х 2
dt
4|13
1 dx1
х2
х1
2 dt

5.

d x1
1 dx1
6
х
10
х
.
1
1
2
dt
2 dt
2
Характеристическое ур–е:
общее решение:
Найдем х 2
x1 С1е С 2 е
t
4t
x1 5 x1 4 x1 0
k 5k 4 0
k1 1
k2 4
2
е
t
ФСР
е
4t
:
1
1 dx1
1
t
4t
t
4t
t
4t
х2
х1 (С1е 4С 2 е ) (С1е С 2 е ) С1е С 2 е
2
2 dt
2
1
t
4t
t
4t
x
С
е
С
е
x 2 С1е С 2 е
общее решение системы: 1
1
2
2
5|13

6.

Метод Эйлера
Будем искать частное решение системы в виде:
x1 1е , x 2 2 е , ... xn n е . (2)
kt
kt
kt
Определим постоянные 1 , 2 ,..., n и k так,
чтобы функции (2) удовлетворяли системе (1):
Сократим на
е
kt
n
kt
kt
k i е a ij j е
j 1
(i 1, n)
(a11 k ) 1 a12 2 a1n n 0,
a21 1 (a22 k ) 2 a2 n n 0,
an1 1 an 2 2
(ann k ) n 0.
6|13
система линейных однородных
алгебраических уравнений
относительно 1 , 2 ,..., n

7.

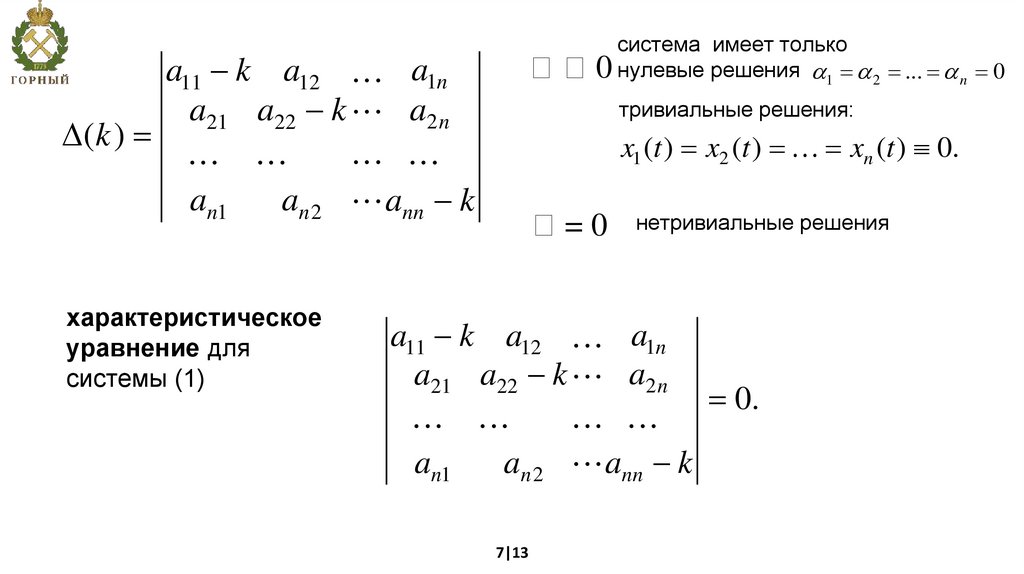
(k )
система имеет только
0 нулевые решения 1 2 ... n 0
a11 k a12 a1n
a21 a22 k a2 n
тривиальные решения:
x1 (t ) x2 (t ) xn (t ) 0.
an1
an 2 ann k
характеристическое
уравнение для
системы (1)
=0
нетривиальные решения
a11 k a12 a1n
a21 a22 k a2 n
an1
an 2 ann k
7|13
0.

8.

Система двух
dx1
dx2
a11 х1 a12 х2 ,
a21 х1 a22 х2 . (3)
ДУ 1–го порядка:
dt
dt
(a11 k ) 1 a12 2 0,
a21 1 (a22 k ) 2 0.
Неизвестные числа 1 , 2
Случай 1: корни характеристического уравнения действительные и
различные
k k1 , k k2
x2
общее решение
системы
(1) k1t
1 е ,
( 2)
x1
2 е ,
( 2)
(1)
x1
(1)
(1) k1t
x2
( 2) k 2t
1 е ,
2
( 2) k 2t
е .
x1 С1 1(1)е k1t С2 1( 2)е k 2 t ,
(1) k1t
( 2) k 2t
x2 С1 2 е С2 2 е ,
8|13
С1, С2– произвольные постоянные

9.

dx1
2 х1 2 х2 ,
dt
Пример 2. Найти общее
решение системы ДУ
2 k
2
0
1
3 k
характеристическое уравнение
Решение системы
ищем в виде:
k1 1
(1)
x1
(1) t
1 е ,
(2 1) 1(1) 2 2 (1) 0,
(1)
(1)
1 1 (3 1) 2 0,
(1)
(1)
0
1 2 2
(1)
(1)
1 2 2
2 0,5
(1)
x1 еt ,
(1)
(1)
1 1.
(1)
x2
0,5е
первое решение системы
t
dx2
х1 3 х2 .
dt
x2 2 е
(1)
(1) t
k1 1, k 2 4
( 2)
x1
и
( 2 ) 4t
1 е ,
x2
( 2)
2 е .
( 2 ) 4t
( 2)
( 2)
k2 4
(2 4) 1 2 2 0,
( 2)
( 2)
1 1 (3 4) 2 0,
x1 С1е С 2 е ,
t
4t
1
t
4t
x 2 С1е С 2 е .
2
общее решение системы
9|13
( 2)
1
2
1
( 2)
( 2)
1
( 2)
4t
x1 е ,
2 ( 2) 1.
x2
( 2)
е
4t
второе решение системы

10.

,
Случай 2: характеристическое уравнение имеет комплексно сопряженные
корни
( 2)
( 2 ) ( i ) t
(1)
(1) ( i ) t
k1 i
1
1
1
1
е
x
k2 i
(1) ( i ) t
x2 2 е
(1)
x
,
, x2
( 2)
е
,
( 2 ) ( i ) t
2 е
.
два частных решения:
(1)
t
x1 е ( 1 cos
( 2)
t
x1 е ( 1 sin
t 2 sin t ),
t 2 cos t ),
соответствующие комбинации этих функций
войдут в общее решение системы
10|13
действительные числа
1 2 1 2
определяются через
1 2
(1)
(1)
( 2)
1
2
( 2)

11.

dx1
dx2
7 х1 х2 ,
2 х1 5 х2 .
dt
dt
Пример 3. Найти общее
решение системы ДУ
характеристическое уравнение
7 k
2
1
0
5 k
k 12k 37 0
2
k1 6 i, k2 6 i.
k 2 6 i
k1 6 i
( 7 6 i ) 1 2 0,
2 1 ( 5 6 i ) 2 0.
( 1 i ) 1 2 0,
2 1 (1 i ) 2 0.
1 1 2 1 i
1 1 2 1 i
( 2)
(1)
( 6 i ) t
(1)
( 2)
( 6 i ) t
( 6 i ) t
( 6 i ) t
.
x2 (1 i )е
. x1 е
x1 е
,
, x2 (1 i )е
Выделить действительную и мнимую компоненты
11|13

12.

x1
(1)
е
( 6 i ) t
е
е
( 6 i ) t
е
6 t
(1 i )е
( 6 i ) t
x2
(1 i )е
x1
( 2)
x2
(cos t i sin t ),
( 6 i ) t
(1)
( 2)
6 t
е
6 t
(cos t sin t ) iе
6t
(cos t sin t )
(cos t i sin t )
е 6t (cos t sin t ) iе 6t (cos t sin t )
Частные решения – отдельно действительные части и отдельно мнимые части
(1)
6t
x1 е cos t ,
( 2)
6t
x1 е sin t
x1 С1е
6t
cos t С2е
общее решение системы ДУ
– линейная комбинация
частных решений
x2
6t
sin t ,
6t
6t
x2 е (cos t sin t ),
(1)
( 2)
6t
е (cos t sin t ).
6t
x2 С1е (cos t sin t ) С2е (cos t sin t )
12|13

13.

Спасибо за внимание
13|13