Similar presentations:
Статическая устойчивость
1. Статическая устойчивость
12. Статическая и динамическая устойчивость
Статическая устойчивость ???Устойчивость в малом. Устойчивость при малых
возмущениях. Применительно к ЭЭС, статическая
устойчивость - это способность электроэнергетической
системы восстанавливать исходное состояние (режим)
после малых его возмущений.
Динамическая устойчивость ???
Устойчивость в большом. Устойчивость при больших
возмущениях. Применительно к ЭЭС, динамическая
устойчивость - это способность электроэнергетической
системы восстанавливать исходное состояние (режим)
после больших возмущений.
2
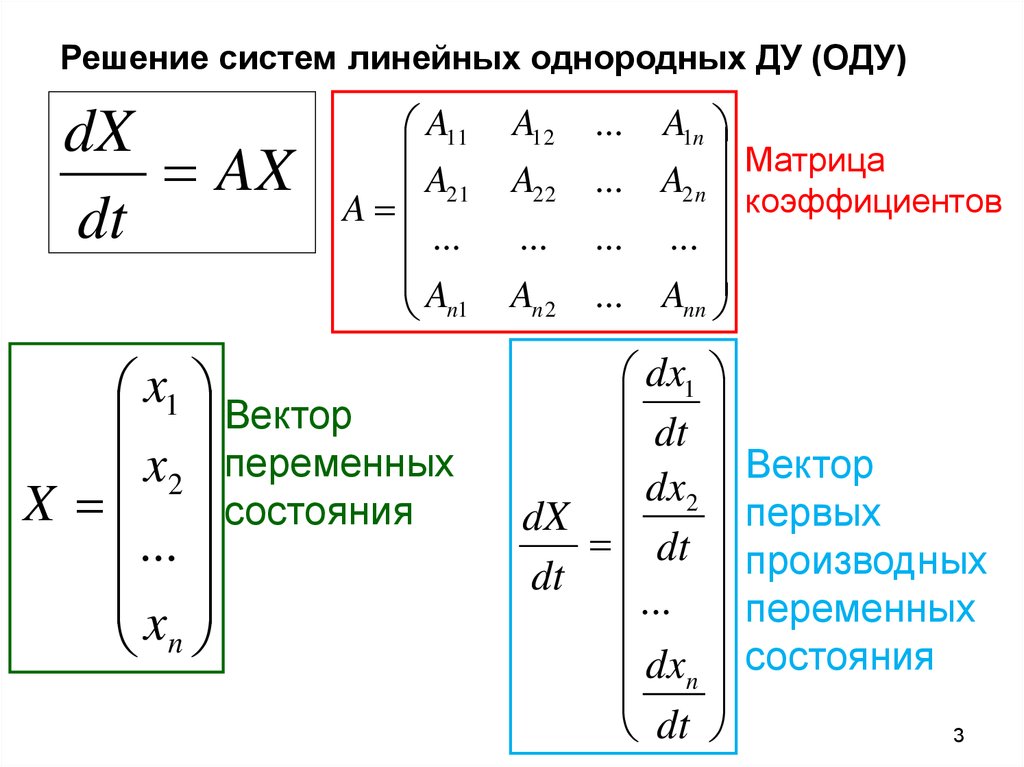
3. Решение систем линейных однородных ДУ (ОДУ)
dXAX
dt
A11
A21
A
...
A
n1
x1 Вектор
x2 переменных
X состояния
...
x
n
A12
A22
...
An 2
A1n
Матрица
... A2 n
коэффициентов
... ...
... Ann
...
dx1
dt
dx2
dX
dt
dt
...
dx
n
dt
Вектор
первых
производных
переменных
состояния
3
4. Решение систем линейных ОДУ
dXAX
dt
Решение системы ОДУ ищется в следующем виде:
n
X Nie
i 1
( λi ) t
N1e
( λ1 ) t
N 2e
( λ2 ) t
... N n e
( λn ) t
λ собственные числа
N -собственные вектора
4
5. Собственные числа и вектора
• Собственный вектор матрицы – вектор,умножение матрицы на который дает тот же
вектор, умноженный на некоторое число,
называемое собственным числом матрицы.
• A – матрица ОДУ;
• N – собственный вектор;
• λ – собственное число.
1 6 2
2
2 • [-1 -6; 2 6] – матрица;
6 1
2
1
• [-2;1], [-3;2] –
1 6 3 3
собственные вектора;
3
6 2 2 • 2 и 3 – собственные числа.
2
AN λN
5
6. Поиск собственных чисел и векторов
AN λNA Eλ N 0
det A Eλ 0
A – матрица ОДУ;
N – собственный вектор;
λ – собственное число.
E – единичная матрица
6
7. Решение систем линейных ОДУ
x t Neλt
x t Ne
t i t
λ ,
λ ,
λ 0.
0.
λ ,
λ ,
λ 0.
0.
t i t
Ne
7
8. Устойчивость системы линейных ОДУ
• Линейная система устойчива, если всесобственные числа имеют отрицательные
действительные части.
• Линейная система неустойчива, если хотя
бы одно собственное число имеет
положительную действительную часть.
• Состояние линейной системы не
определено, если одно или более
собственных чисел имеют действительную
часть равную нулю, а все остальные
собственные числа имеют отрицательные
действительные части.
8
9. Анализ устойчивости системы нелинейных ДУ
dXAX
dt
dX
dt
f1 X 0
x1
f X
f X 0 2 0
x1
X
...
f n X 0
x
1
dX
f X
dt
f X 0
X
f1 X 0
x2
f 2 X 0
x2
...
f n X 0
x2
X
f1 X 0
xn
f 2 X 0
...
xn
...
...
f n X 0
...
xn
...
Матрица Якоби
Якобиан
9
10. Устойчивость системы НЕлинейных ДУ
• Если все собственные значенияякобиана имеют отрицательные действительные
части, то нулевое решение X = 0 исходной системы
и линеаризованной является устойчивым.
• Если хотя бы одно собственное значение
якобиана имеет положительную действительную
часть, то нулевое решение X = 0 исходной системы
и линеаризованной системы вляется неустойчивым.
10
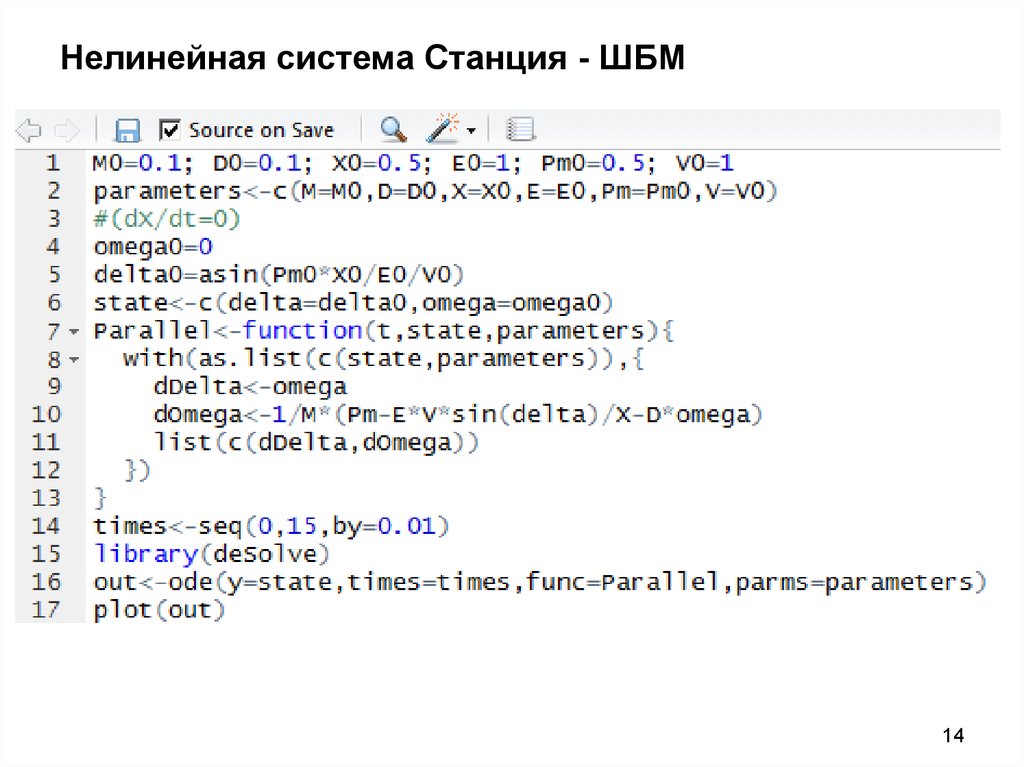
11. Нелинейная система Станция - ШБМ
d,
dt
d 1
dt M
EV
P
sin
D
m
.
X
f X 0
1
X
M
EV
P
sin
D
m
X
1
EV
Pm
sin D
X
M
11
12. Нелинейная система Станция - ШБМ
0f X 0
EV
cos
X
MX
0
det EV
cos
MX
1
D
M
1
D
M
D
EV
cos 0
M MX
2
2
D
D 4 EV
x1
cos
M
MX
M
2
D
EV
cos 0
M
MX
x2
D
D 4 EV
cos
M
MX
M
12
13. Анализ собственных чисел системы ШБМ
• Проведем анализ на тестовой схеме со следующимипараметрами: M0=0.1; D0=0.1; X0=0.5; E0=1;
Pm0=1.5; V0=1.
• D/M=1, 4EV/MX=4/(0.1*0.5)=80.
• X1=-1 + sqrt(1-80*cos(δ));
• X2=-1 - sqrt(1-80*cos(δ));
• δЄ[0, π/2); cos(δ) Є[1, 0), X1 и X2 – комплексные числа
с отрицательной действительной частью. Система
статически колебательно устойчива.
• δЄ[π/2, π]; cos(δ) Є(0, -1], как минимум одно
положительное действительное собственное число.
Система статически апериодически НЕустойчива.
• δ≡π/2, неопределенная ситуация, так как X1 ≡ 0, X2<0.
13
14. Нелинейная система Станция - ШБМ
1415. Анализ статической устойчивости ШБМ
• δ≡π/2 – точка, отделяющая состояния устойчивогои неустойчивого равновесий. При δ≡π/2 Pm0max
≡2.0.
• Рассмотрим положительное и отрицательное
малые изменения мощности вблизи точки δ≡π/2.
• В соответствии с предшествующим анализом,
система должна быть статически колебательно
устойчива при отклонении Pm0max-dP и
статически апериодически неустойчива при
Pm0max+dP, где dP – малое изменение
механической мощности турбины.
15
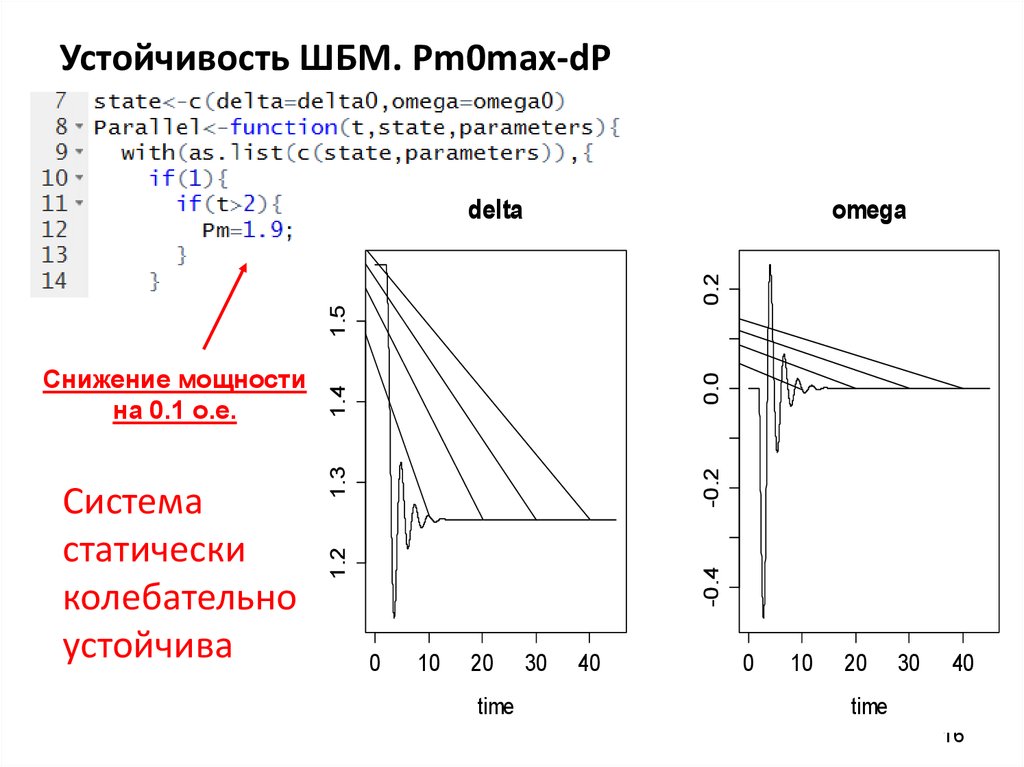
16. Устойчивость ШБМ. Pm0max-dP
omega1.4
-0.2
1.3
-0.4
Система
статически
колебательно
устойчива
1.2
Снижение мощности
на 0.1 о.е.
0.0
1.5
0.2
delta
0
10
20
time
30
40
0
10
20
30
40
time
16
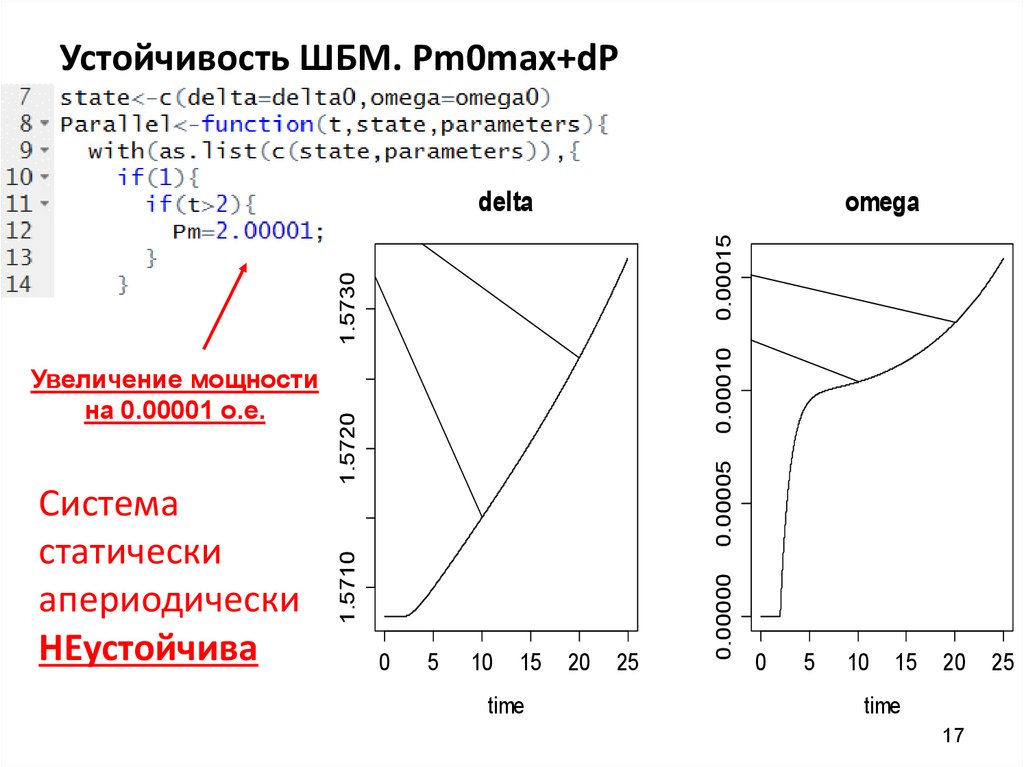
17. Устойчивость ШБМ. Pm0max+dP
omega0.00005
1.5720
0
5
10
15
time
20
25
0.00000
Система
статически
апериодически
НЕустойчива
1.5710
Увеличение мощности
на 0.00001 о.е.
0.00010
1.5730
0.00015
delta
0
5
10
15
20
time
17
25
18. Работа в статически неустойчивой точке
• δ0=0.93рад=53град. – статически устойчиваяточка, которой соответствует Pm0=1.6о.е.
• δ0= π - 0.93рад=127град. – статически
НЕустойчивая точка, которой также соответствует
Pm0=1.6о.е.
• Аналогично. Рассмотрим положительное
(Pm0+dP) и отрицательное (Pm0-dP) малые
изменения мощности вблизи точки δ0= π 0.93рад=127град.
18
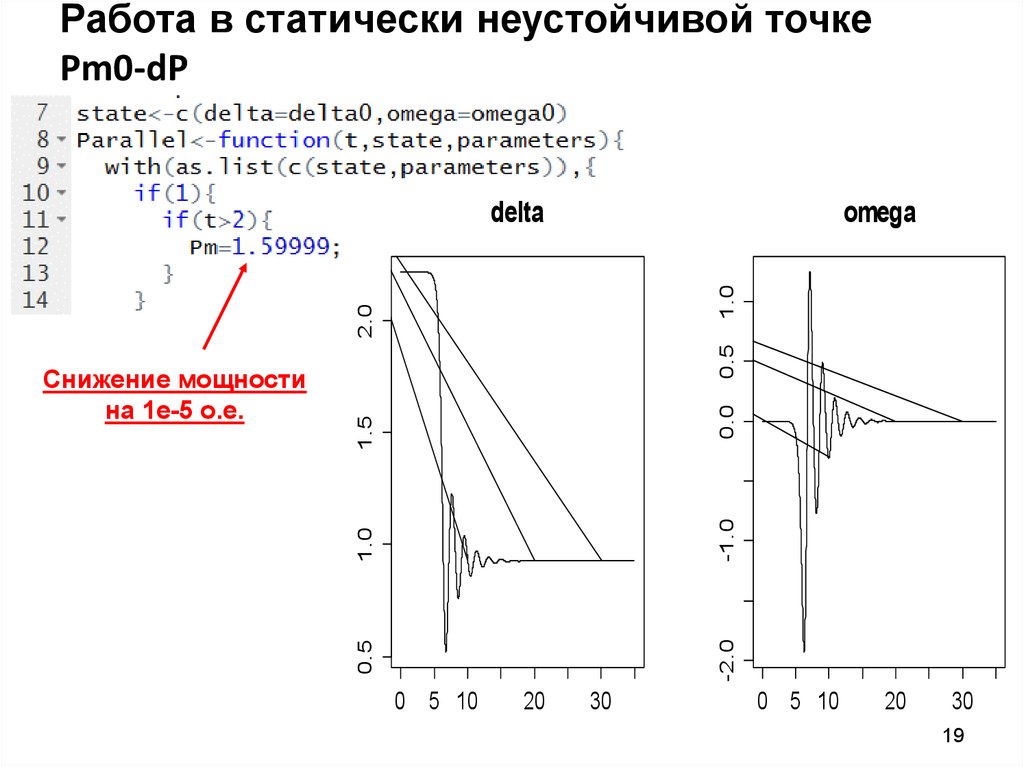
19. Работа в статически неустойчивой точке Pm0-dP
delta0.0
-1.0
1.5
-2.0
1.0
0.5
Снижение мощности
на 1e-5 о.е.
0.5
2.0
1.0
omega
0 5 10
20
time
30
0 5 10
20
time
30
19
20. Работа в статически неустойчивой точке Pm0+dP
omega10
80
60
5
40
0
20
0
Увеличение мощности
на 1e-5 о.е.
100
15
140
delta
0
5
10
time
15
0
5
10
time
15
20















 mathematics
mathematics








