Similar presentations:
Динамика_4
1. Лекция 4
Теорема об изменении количества движения:количество движения; импульс силы;
теорема об изменении количества движения;
закон сохранения количества движения.
2.
Количество движения, импульс силыИмпульс силы – мера механического взаимодействия,
характеризующая передачу механического движения со
стороны действующих на точку сил за данный промежуток
времени.
Элементарный импульс силы: dS F dt
t2
Импульс силы за конечный промежуток времени t: S F dt
t1
В проекциях на координатные оси:
t2
t
( x) : S x FX dt ;
t2
t
( y ) : S y FY dt ;
1
t
( z ) : S z FZ dt.
1
В случае постоянной силы:
S x FX (t2 t1 );
t2
1
S F (t 2 t1 ).
S y FY (t2 t1 );
S z FZ (t2 t1 );
Единицей измерения импульса силы в системе СИ является 1 кг м/с = 1 Н с
3.
Количество движения точки – мера механическогодвижения, определяемая вектором, равным произведению
массы точки на вектор ее скорости:
Q
v
m
Q mv .
Количество движения системы материальных точек –
геометрическая сумма количеств движения материальных
точек:
Q Q1 Q2 ... Qn Qk .
Вектор количества движения системы (твердого тела) равен
произведению массы всей системы на вектор скорости центра
масс системы:
Q MvC
Qx M x C ;
Qy M y C ;
Qz M z C .
4.
Теорема об изменении количества движенияТак как масса точки постоянна, запишем для точки
дифференциальное уравнение движения в виде:
d (mv )
dt
F
k
производная по времени от количества движения
точки равна геометрической сумме действующих на
точку сил.
t1
После интегрирования получаем: mv mv0
t2
Fk dt
0
Так как S F dt окончательно получаем:
- теорема об изменении
t1
mv mv0
S k количества движения
материальной точки
Теорема: изменение количества
движения точки за некоторый
промежуток
времени
равно
геометрической сумме импульсов
всех действующих на точку сил за
тот же промежуток времени.
В проекциях на оси
Skx ,
mv1 y mv0 y S ky ,
mv1z mv0 z S kz.
mv1x mv0 x
5.
Теорема об изменении количества движения системы:Рассмотрим
систему
n
материальных
точек.
Приложенные к каждой точке силы разделим на внешние и
внутренние и заменим их на соответствующие
равнодействующие Fke и Fki. Запишем для каждой точки
основное уравнение динамики:
dvk
mk
mk ak Fke Fki
dt
Просуммируем эти уравнения
dvk
d
по всем точкам:
e
i
( mk vk ) R e
mk
Fk
Fk ;
dt
dt
R e Ri 0
Из определения количества движения системы: mk v k Q .
dQ
- теорема об изменении количества движения
Re
системы
dt
Производная вектора количества движения системы по
времени равна главному вектору внешних сил системы.
6.
dQxR ex
dt
t1
e
FXk ;
dQy
dt
Ry
e
FYke ;
dQz
R ez
dt
FZke .
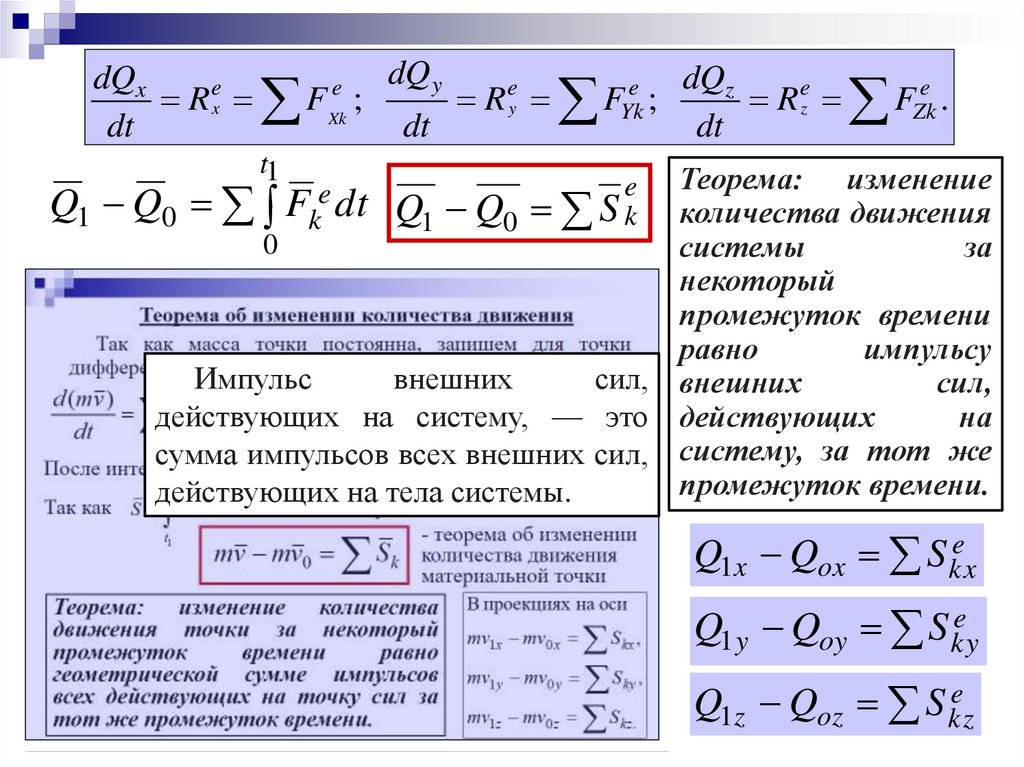
Теорема: изменение
Q1 Q0
количества движения
системы
за
некоторый
промежуток времени
равно
импульсу
Импульс
внешних
сил, внешних
сил,
действующих на систему, — это действующих
на
сумма импульсов всех внешних сил, систему, за тот же
промежуток времени.
действующих на тела системы.
Q1 Q0 Fke dt
0
e
Sk
e
Q1x Qox S kx
e
Q1 y Qoy S ky
e
Q1z Qoz S kz
7.
Закон сохранения количества движения системыСледствия из теоремы об изменении количества движения
системы:
1. Если в интервале времени [t1, t2] главный вектор внешних
сил системы равен нулю, Re = 0, то вектор количества
движения постоянен Q = const:
dQ
e
dt
Fk 0
2. Если в интервале времени [t1, t2] проекция главного
вектора внешних сил системы на ось X равна нулю, Rxe = 0, то
проекция количества движения системы на ось X постоянна,
Qx = const:
dQ
e
x
dt
Fkx 0
Аналогичные утверждения справедливы для осей Y и Z.






 physics
physics








