Динамика

1. Динамика

Динамикой называется раздел механики, в котором изучаются законы
движения материальных тел под действием сил.
1. Введение в динамику.
В динамике изучаются как постоянные, так и переменные силы.
Переменные силы зависят от:
1) времени (сила тяги мотора при разгоне),
2) положения тела (сила тяготения, сила упругости пружины),
3) скорости (сила сопротивления воздуха).
Инертность – свойство материальных тел быстрее или медленнее
изменять скорость своего движения под действием приложенных сил.
Величина, зависящая от количества вещества данного тела и определяющая
меру его инертности, называется массой тела.

2.

В общем случае движение зависит от:
-его массы,
-приложенных сил,
-геометрических размеров,
-распределения массы по телу,
-чистоты обработки поверхности, формы тела и т.д.
Материальная точка – это материальное тело, имеющее массу, размерами
которого при изучении его движения можно пренебречь.
Курс динамика разбивается на 2 основные части:
1) динамика точки;
2) динамика системы материальных точек или твердых тел.
1.1 Законы динамики
И. Ньютон объединил законы в труде
«Математические начала натуральной философии», 1686.
1. Закон инерции (Галилей, 1638).
Изолированная от внешних воздействий материальная точка сохраняет
свое состояние покоя или равномерного прямолинейного движения до тех пор,
пока приложенные силы не заставят ее изменить это состояние.

3.

Равномерное прямолинейное движение называется движением по инерции.
Система отсчета, по отношению к которой выполняется первый закон,
называется инерциальной системой отсчета (иногда ее называют
неподвижной).
2. Основной закон динамики (Гук, 1660-е годы).
Произведение массы точки на ускорение, которое она получает под
действием данной силы, равно по модулю этой силе, а направление ускорения
совпадает с направлением силы.
mW F
или для модулей
m W F
Если F=P – вес тела, а ускорение W=g, то
P m g или m P / g - связь между массой тела и ее весом.
3. Закон равенства действия и противодействия.
Две материальные точки действуют друг на друга с силами, равными по
модулю и направленными вдоль прямой, соединяющей эти точки, в
противоположные стороны.

4.

2. Динамика точки
2.1. Дифференциальные уравнения
движения точки и их интегрирование
2.1.1 Задачи динамики для свободной и
несвободной материальной точки
Для свободной материальной точки:
1) Зная закон движения точки, определить действующую на нее силу.
d 2S
W 2
mW F
dt
2) Зная действующие на точки силы, определить закон движения точки.
F
W
m
S Wdt
Для несвободной точки (благодаря наложенным связям, точка вынуждена
двигаться по заданной неподвижной поверхности или кривой):
1) Зная движение точки и активные силы F , определить реакцию связи N .
mW F N
2) Зная действующие на точку активные силы, определить:
- закон движения точки;
- реакцию наложенной связи.

5.

2.1.2 Прямолинейное движение точки
Материальная точка М движется прямолинейно под действием силы
Точка М – свободная.
R
.
Т.к. точка свободная, то двигаться по
оси X она будет только тогда, когда
R RX // Ox
W WX // Ox
Уравнение основного закона динамики:
d 2x
m 2 FiX
dt
m WX R X FiX
d 2x
WX 2
dt
- это дифференциальное уравнение движения точки.
m
dVX
FiX
dt
dx
VX
dt
- начальные условия (при t =0):
x = x0; Vx Vx 0
Задача Коши
Иногда надо найти зависимость скорости от перемещения X (а не от времени t)
dV X dV X dx dV X
VX
dt
dx dt
dx
тогда
m VX
dVX
Fi
dx
dx
VX
dt

6.

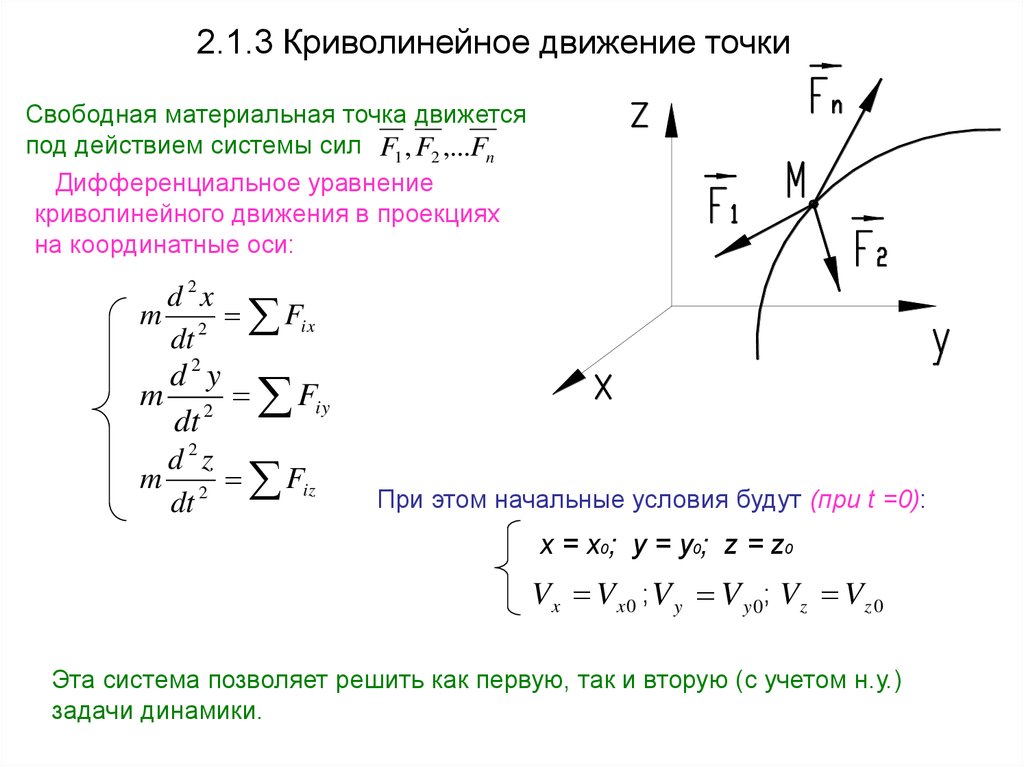
2.1.3 Криволинейное движение точки
Свободная материальная точка движется
под действием системы сил F1 , F2 ,...Fn
Дифференциальное уравнение
криволинейного движения в проекциях
на координатные оси:
d 2x
m 2 Fix
dt
d2y
m 2 Fiy
dt
d 2z
m 2 Fiz
dt
При этом начальные условия будут (при t =0):
x = x0; y = y0; z = z0
V x V x 0 ; V y V y 0; V z V z 0
Эта система позволяет решить как первую, так и вторую (с учетом н.у.)
задачи динамики.

7.

2.2. Колебания материальной точки
2.2.1 Свободные колебания без учета сил сопротивления
Точка М движется прямолинейно под действием
восстанавливающей силы F , направленной к
неподвижному центру О и пропорционально
расстоянию от этого центра.
F Fx c x
d 2x
m 2 с х
dt
- упругая сила, сила притяжения.
- дифференциальное уравнение движения.
d 2x
2
k
x 0
2
dt
Пусть
с
k2
m
- диф. уравнение свободных колебаний без сопротивления
Решим его, составив характеристическое уравнение:
2 k 2 0
1, 2 i k
x C1 sin kt C2 cos kt

8.

С1 а cos
Вводим постоянные а и :
C 2 a sin
тогда
x a (sin kt cos cos kt sin
x a sin kt
- закон гармонических колебаний.
а – амплитуда колебаний, kt - фаза колебаний,
- начальная фаза колебаний (если = 0 – то колебания идут по закону
синуса, при =
- по закону косинуса.),
2
k – круговая частота колебаний, Т – период колебаний (время одного полного
колебания):
T
2
k
1
k
- частота колебаний (число колебаний в секунду).
T 2
Постоянные интегрирования а и найдем из начальных условий:
при t =0:
x = x0; Vx Vx 0
из закона гармонических колебаний:
x0 a sin
V0 ak cos
V x x ak cos kt
Решив систему:
a
2
V
x 02 02
k
k x0
tg
V0

9.

2.2.2 Влияние постоянной силы на свободные
колебания точки
На точку М действуют:
1) F - восстанавливающая сила;
2) Р - постоянная сила.
F c OM
Р = const.
В этом случае положение равновесия будет в точке О1, когда F P или
c ст Р
ст
Р
с
- статическое отклонение точки.
F x c x ст Px P
2
d
x
2
отсюда получим диф. уравнение вида:
k
x 0
2
dt
Таким образом, сила Р не изменяет характера колебаний, совершаемых
Если взять О1 за начало отсчета, то
точкой под действием восстанавливающей силы F , а только смещает центр
этих колебаний в сторону действия силы Р на величину статического
отклонения ст .
P
k2
m ст
T 2
m ст
Р

10.

2.2.3 Затухающие колебания
Рассмотрим тот вариант, когда в свободных
колебаниях сила сопротивления
пропорциональна скорости.
R x - сила сопротивления среды.
F c x - восстанавливающая сила.
Диф. уравнение движения будет иметь вид:
2
Примем: k
с
m
2b
Тогда:
d 2x
dx
m 2 с х
dt
dt
m
d 2x
dx
2
2
b
k
x 0
2
dt
dt
(*)
Решим полученное уравнение:
2 2b k 2 0 - характеристическое уравнение
Корни этого уравнения:
1, 2 b b 2 k 2
При таких корнях характеристического уравнения, может быть 2 случая
решения этого уравнения.

11.

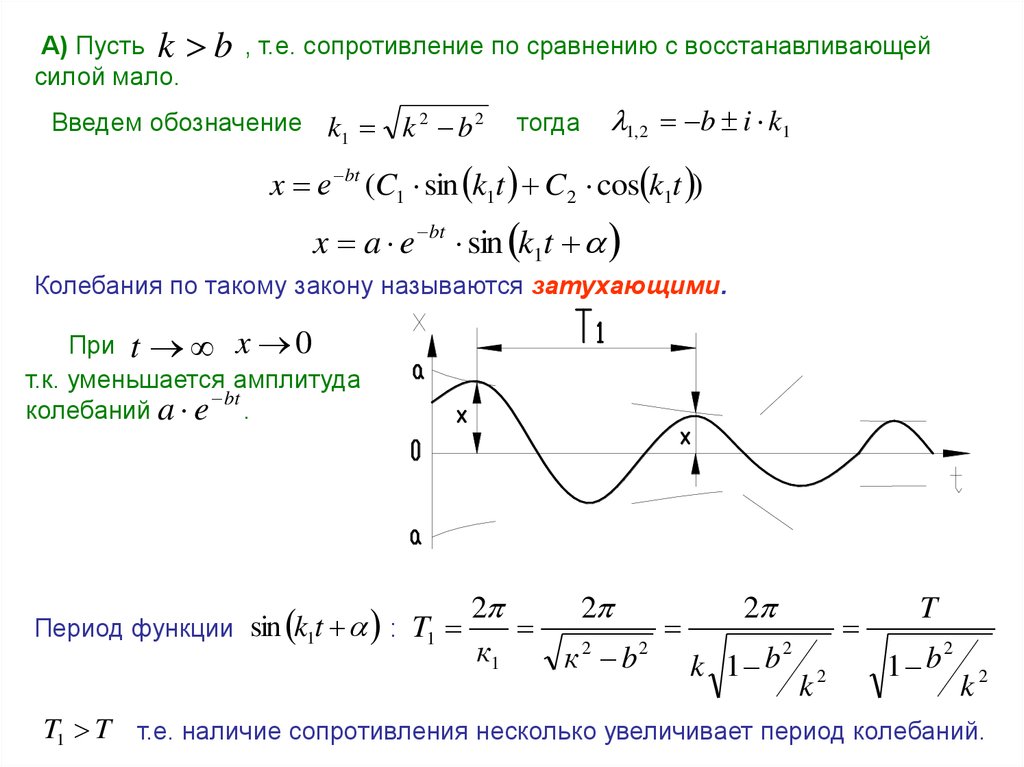
А) Пусть k b , т.е. сопротивление по сравнению с восстанавливающей
силой мало.
Введем обозначение k
1
k 2 b2
тогда
1, 2 b i k1
x е bt (C1 sin k1t C2 cos k1t )
x a e bt sin k1t
Колебания по такому закону называются затухающими.
При t x 0
т.к. уменьшается амплитуда
bt
колебаний a e .
Период функции sin k1t :
T1
2
2
2
к1
к 2 b2 k 1 b2
k2
T
2
b
1
k2
T1 T т.е. наличие сопротивления несколько увеличивает период колебаний.

12.

Максимальные амплитуды колебаний каждый раз уменьшаются на
xn 1 xn e bT1
e bT1
т.е. по закону геометрической прогрессии.
- декремент колебаний;
bT1
- логарифмический декремент колебаний.
А) Пусть b k , т.е. сопротивление по сравнению с восстанавливающей
силой велико.
Введем обозначение: b 2 k 2 r 2
тогда из уравнения (*)
1, 2 b r
x C1 e (b r ) t C2 e (b r ) t
Движение точки не будет колебательным.
2.2.4 Вынужденные колебания
Пусть на точку, кроме восстанавливающей силы F, действует еще
вынуждающая сила Q , проекция которой на ось Ох равна:
Qx Q0 sin pt
В этом случае колебания называются вынужденными.
р – частота вынуждающей силы.
Qx
называют гармонической возмущающей силой.

13.

2.2.4.1. Вынужденные колебания при
отсутствии сопротивления
В этом случае диф. уравнение имеет вид:
Q0
P0
заменим
m
k2
с
m
тогда
d 2x
m 2 с х Q0 sin pt
dt
d 2x
2
k
x P0 sin pt
2
dt
Решим линейное неоднородное диф. уравнение: x xO.O. xЧ . Н
x a sin kt
P0
sin pt
2
2
k p
Вынужденные колебания с
амплитудой, не зависящей от
н.у., и частотой р.
Обычно собственные колебания довольно быстро затухают и через время t
колебания определяются только вторым слагаемым.
P0
Амплитуда вынужденных колебаний: А
Собственные колебания
с амплитудой а и частотой к.
При
p k
k 2 p2
имеет место резонанс, т.е.
A

14.

2.2.4.2. Вынужденные колебания при наличии
сопротивления
F c x
R x
Qx Q0 sin pt
На точку действует: восстанавливающая сила
сила сопротивления
возмущающая сила
Диф. уравнение этого движения имеет вид:
d 2x
dx
m 2 с х
Q0 sin pt
dt
dt
d 2x
dx
2
2
b
k
x P0 sin pt
2
dt
dt
Решение этого неоднородного уравнения имеет вид:
x a e bt sin k1t А sin pt
А
k
Р0
2
p2
2
4 b2 p2
2b p
arctg 2
2
k p
- амплитуда вынужденных колебаний
- сдвиг фазы вынужденных колебаний по отношению к
возмущающей силе.

15.

2.3 Общие теоремы динамики точки
-являются следствиями основного закона динамики;
-они устанавливают наглядные зависимости, между соответствующими
динамическими характеристиками движения материальных тел;
-применение этих теорем избавляет от необходимости проделывать для
каждой задачи те операции интегрирования, которые раз и навсегда
производятся при выводе этих теорем; тем самым упрощается процесс
решения.
Основные динамические характеристики:
1. Количеством движения материальной точки называется
векторная величина, равная произведению массы точки на ее
скорость.
2
2. Кинетической энергией материальной точки называется
mV
скалярная величина, равная половине произведения массы Е К
2
точки на квадрат ее скорости.
3. Импульсом силы называется векторная величина,
характеризующая действие силы з некоторый промежуток d S F dt
t1
времени.
t1
t1
t1
Q mv
S Fdt
0
S x Fx dt
0
S y Fy dt
0
S z Fz dt
0

16.

4. Элементарная работа силы dA равна скалярному
произведению вектора силы на вектор элементарного
перемещения точки
dA F d r
Можно представить это уравнение в координатной форме:
dA FX dx FY dy FZ dz
Полная работа силы на любом конечном перемещении М0 М1 равна взятому
вдоль этого перемещения криволинейному интегралу второго типа от
элементарной работы:
М1
A
F dr
или
A
М0
М1
F
X
dx FY dy FZ dz
М0
5. Мощность определяет работу, совершаемую силой за единицу времени.
A
W
t
или в общем случае:
dA прS F d s
W
прS F v
dt
dt
т.е. мощность равна произведению проекции силы на направление движения
на скорость движения.

17.

2.3.1 Теорема об изменении количества движения точки
Теорема: Изменение количества движения точки за некоторый промежуток
времени равно геометрической сумме импульсов всех действующих на точку
сил за тот же промежуток времени.
mV1 mV0 S i
Доказательство.
Основное уравнение динамики:
dV
m
F i
dt
Так как масса точки постоянна, то уравнение, выражающее основной закон
динамики, можно представить в виде
d (mV )
Fi
dt
Проинтегрируем это уравнение, считая, что при t 0 0 , V V0 , а при
V1
t1
t t1 , V V1 :
d (mV ) Fi dt mV1 mV0 S i
V0
Представим полученное
уравнение в проекциях на оси:
0
mV1x mV0 x S ix
mV1 y mV0 y Siy
mV1z mV0 z Siz

18.

2.3.2 Теорема об изменении кинетической энергии точки
Теорема. Изменение кинетической энергии точки при некотором ее
перемещении равно алгебраической сумме работ всех действующих на точку
сил на том же перемещении.
mV12 mV02
Ai ( M 0 M 1 )
2
2
Доказательство.
Fi
Основное уравнение динамики: mW
Проектируя обе его части на касательную к траектории точки М
ось , получим:
mW F i
касательное ускорение можно представить в виде:
m V
dV
F i
dS
W
dV dS
dV
V
dt dS
dS
Умножим обе части этого равенства на ds и внесем тV под знак
дифференциала (причем Fi dS dAi - элементарная работа):
mV 2
dAi
d
2
Представим результат в конечных разностях:
mV12 mV02
Ai ( M 0 M 1 )
2
2

19.

!
При несвободном движении точки кроме работы активных сил в правую
часть войдет и работа реакций связи. В частном случае, когда реакция будет
направлена по нормали к траектории точки, работа ее равна нулю.
!
Если траектория (поверхность) не является гладкой, то в правой части
добавится работа сил трения.
2.3.3 Теорема об изменении момента количества движения
mv
– вектор количества движения,
mo mV
или
mz mV
- момент количества движения точки или
кинетический момент относительно центра О или
оси Оz.
Вычисляется момент количества движения
также как и момент силы.
mo mV
m V h
где h – длина перпендикуляра, опущенного из
центра О на направление вектора mV

20.

Теорема моментов относительно оси устанавливает связи между
и
m z mV
mz F
Как мы уже знаем m z F x Fy y Fx
Аналогично и для величины m mV
z
:
mz mV m x V y y Vx
Продифференцируем обе части равенства по t:
dV y
dV
d
dx
dy
[mZ (mV )] m ( V y Vx ) ( x m
y m x )
dt
dt
dt
dt
dt
0
Таким образом имеем:
d
[mZ (mV )] mZ ( F )
dt
Fy
Fx
Теорема: Производная по времени от момента количества движения точки
относительно какой-нибудь оси равна моменту действующей силы
относительно той же оси.

21.

Аналогичная теорема доказана и для момента относительно любого
неподвижного центра О. d
dt
[mО (mV )] mО ( F )
Из теоремы следует, что если
mz F 0 , то mZ (mV ) const
2.4 Динамика относительного движения точки
Законы динамики и полученные из них в предыдущих главах уравнения и
теоремы верны только для абсолютного движения точки, т.е. движения по
отношению к инерциальной (неподвижной) системе отсчета.
Рассмотрим относительное движение точки, т.е.
движение по отношению к неинерциальной системе
отсчета. Пусть точка М движется под действием
приложенной к ней системы сил
n
F 1 F 2 ... F n Fi
i 1
Oxyz – система отсчета, которая движется по
известному нам закону относительно неподвижной
системы отсчета O1x1y1z1.
Нас интересует относительное движение точки М, т.е. движение
относительно Oxyz.

22.

Для абсолютного движения основной закон динамики:
Из кинематики известно, что
Wотн W
m Wабс Fi
Wабс Wотн Wпер Wкор
m (Wотн Wпер Wкор ) Fi
- ускорение изучаемого нами относительного движения
m W Fi ( m Wпер ) ( m Wкор )
и
m Wпер Fпер
- переносная компонента силы инерции
и
m Wкор Fкор
- кориолисова компонента силы инерции
и
и
m W Fi Fпер
Fкор
Это основной закон динамики для относительного движения точки
Все уравнения и теоремы динамики для относительного движения точки
составляем точно так же, как и для абсолютного, но при этом к действующим на
точку силам взаимодействия с другими телами ( F ) добавляем переносную
i
и кориолисову ( F и ) силы инерции. ( F и )
пер
кор

23.

и
и
и Fкор
учитывают влияние на относительное движение точки
Fпер
перемещения подвижных осей.
Частные случаи:
и
0
1) Если подвижные оси перемещаются поступательно, то Fкор
и
m W Fi Fпер
2) Если подвижные оси перемещаются поступательно, прямолинейно и
равномерно, то F и F и 0 и закон относительного движения будет иметь вид:
пер
кор
mW F i
Следовательно, такая система отсчета также будет инерциальной.
!
Из этих результатов, вытекает, что никаким механическим экспериментом
нельзя обнаружить, находится ли данная система отсчета в покое или
совершает поступательное, равномерное и прямолинейное движение.
В этом состоит открытый Галилеем принцип относительности
классической механики.
3) Если точка по отношению к подвижным осям находится в покое, то для нее
и
W 0 , V 0 , а следовательно Fкор 0 , т.к. Wкор 2 пер Vотн sin
отн
Тогда равенство примет вид:
и
Fi Fпер
0 - это уравнение относительного равновесия (покоя) точки.

24.

4) При составлении уравнений относительного движения в случае, когда
и
Fкор
0 надо иметь в виду, что: а)
и
Fкор
m Wкор 2 m пер Vотн
и
следовательно, Fкор Vотн V а значит и к касательной к относительной
траектории точки.
и
Тогда основное уравнение динамики в относительном движении в
Fкор
_ 0
проекции на касательную будет иметь вид:
dV
и
Fi Fпер
dt
и
оси , то
А( Fкор
) 0
m
б) т.к. сила
Теорема об изменении кинетической энергии в относительном движении
будет иметь вид:
2
2
mV1 mV0
и
Ai А( Fпер
)
2
2
Во все остальные уравнения относительного движения будут в общем
случае входить F и и F и
пер
кор

25.

3. Динамика системы
3.1 Введение в динамику системы
Механической системой материальных точек (тел) называется такая их
совокупность, в которой положение или движение каждой точки (тела) зависит
от положения или движения всех остальных.
Твердое тело – это система материальных точек (тел), образующих это
тело, между которыми отсутствуют относительные движения.
Силы, действующие на твердые тела системы:
1) Внешние – действуют на твердые тела системы со стороны точек или тел,
не входящих в состав данной системы (
) Fe
2) Внутренние – действуют на точки системы со стороны других точек той
же системы ( F i )
Эти силы могут быть как активными, так и реакциями связей. Разделение
сил на внешние и внутренние условно.
Свойства внутренних сил:
F
2) m
1)
i
k
0
i
(
F
O
k ) 0
i
m
(
F
x k) 0

26.

!
Внутренние силы в ряде случаев могут вызывать взаимные перемещения
точек системы. Полностью уравновешенны внутренние силы только в
абсолютно твердом теле.
n
Масса системы:
М mk
Где
mk
- массы точек системы.
1
Положение центра масс (цента инерции) совпадает с центром тяжести
системы и определяется по формулам:
mк yк
mк хк
mк zк
yС
хС
zС
M
M
M
3.1.1 Момент инерции тела относительно оси.
Радиус инерции.
Положение центра масс не полностью характеризует
распределение масс системы.
При увеличении или уменьшении h центр масс не
изменится, хотя распределение масс стало иным и это
скажется при вращательном движении системы.

27.

Момент инерции системы (тела) относительно данной оси Oz (или осевой
момент инерции) – это скалярная величина, равная сумме произведений масс
всех точек системы (тела) на квадрат их расстояний до этой оси.
J z mk hk2
Если расстояния точек от координатных осей выражены через координаты xk,
yk, zk, то расстояние, например, до оси Oz: h 2 x 2 y 2
k
k
k
Тогда моменты инерции системы относительно координатных осей находятся
по формулам:
J x mk ( yk2 zk2 )
J y mk ( zk2 xk2 )
J z mk ( xk2 yk2 )
Для сплошного тела:
Jz
2
h
dm
(V )
2
h
dV
(V )
2
2
(
y
x
)dV
(V )
Для неоднородных тел сложной формы момент инерции относительно оси
можно определить экспериментально:
2
и
- радиус инерции.
J z M и

28.

3.1.2 Теорема Гюйгенса.
Теорема: Момент инерции тела относительно любой
оси равен моменту инерции (относительно оси ей
параллельной и проходящей через центр масс тела)
сложенному с произведением массы тела на квадрат
расстояния между осями.
J Оz J Cz M d 2
3.1.3 Центробежные моменты инерции.
Главные оси инерции.
Асимметрию в распределении масс
учитывают
центробежными моментами инерции.
J xy mk xk yk
J yz mk yk zk
J zx mk zk xk
В отличие от осевых моментов инерции, центробежные могут быть:
-Как положительные, так и отрицательные;
-Равны нулю (если ось z есть ось симметрии системы или тела, то в этом
случае J zx 0 J yz 0

29.

Главной осью инерции тела для точки О называется ось Оz, для которой
J yz 0
J zx 0
Главный момент инерции тела – это момент инерции тела относительно
главной оси инерции.
Главными центральными осями инерции тела называются главные оси
инерции, построенные для центра масс тела.
Если по главным осям инерции направить координатные оси, то все
центробежные моменты инерции будут равны нулю, что существенно упростит
формулы и уравнения динамики.
3.2 Дифференциальные уравнения
движения системы
Система состоит из h материальных точек. Для каждой точки запишем
e
i
основное уравнение динамики:
mк Wк Fk Fk
Fke
- равнодействующая всех внешних сил,
Fki
- равнодействующая внутренних сил.
Тогда для всей системы точек получим дифференциальные уравнения
системы материальных точек в векторной форме:

30.

m1 W1 F1e F1i
m2 W2 F2e F2i
- это диф. уравнения движения системы
материальных точек в векторной форме.
………………
mn Wn Fne Fni
Спроектировав все векторы из полученной системы на координатные оси,
получим диф. уравнения системы в координатной форме:
m1 W1x F1ex F1ix
m1 W1 y F1ey F1iy
m1 W1z F1ez F1iz
m2 W2 x F2ex F2ix
………………….
mn Wnz Fnze Fnzi
Основная задача динамики: Зная заданные
силы проинтегрировать диф. уравнения и найти
закон движения каждой точки системы.
Этот путь слишком сложен и почти всегда
связан с непреодолимыми математическими
трудностями.
Обычно на практике достаточно знать некоторые суммарные характеристики
движения системы в целом, а не каждой ее точки.
Суммарные характеристики движения системы материальных точек можно
найти при помощи общих теорем динамики системы.

31.

4. Общие теоремы динамики
4.1 Теорема о движении центра масс
Для определения характера движения системы (особенно твердого тела) в
ряде случаев достаточно знать закон движения ее центра масс.
Сложим почленно полученную систему:
e
i
m
W
F
F
к к k k
Преобразуем левую часть равенства, учитывая, что
2
mк Wк mk
Т.к. для системы
системы:
F
2
d rk
d rc
M
M Wc
2
2
dt
dt
i
k
m
k
r k M rc
где с – центр масс системы.
0 то получим теорему движения центра масс
М Wc Fke
Теорема: Центр масс системы движется как
материальная точка, масса которой равна массе всей
системы и к которой приложены все внешние силы,
действующие на систему.
В координатной форме:
d 2 xc
М 2 Fkxe
dt
d 2 yc
М 2 Fkye
dt
d 2 zc
М 2 Fkze
dt

32.

Значение теоремы:
1) Дает обоснование методом динамики точки в приложении к динамике
системы точек (определяет закон движения центра масс системы).
Если тело движется поступательно, то его движение полностью
определяется движением центра масс.
2) Позволяет исключит все (как правило неизвестные) внутренние силы.
4.2 Закон сохранения движения центра масс
Следствия из теоремы:
Если F 0 , то Wc 0 и Vc const
е
k
Это значит, что центр масс движется с постоянной по модулю и направлению
скоростью, т.е. равномерно и прямолинейно (или остается в покое). Таким
образом, действие внутренних сил движение центра масс изменить не может.
То же можно сказать и о проекциях на какую-либо ось:
Если
F
е
kx
0 , то Vcx const
ПРИМЕР. Действие пары сил на тело:
F1 F1, 0 ,следовательно, если центр масс был
неподвижным, то он неподвижным и останется, а тело
начнет вращаться вокруг своего центра масс (если h1 h2 )

33.

Рекомендации по решению задач:
1) Рассматриваемую систему необходимо выбрать так, чтобы наперед
неизвестные силы сделать внутренними.
2) Если имеет место закон сохранения движения центра масс, то теорема
позволяет по перемещению одной части системы найти перемещение другой ее
части.
4.3 Теорема об изменении количества
движения системы
Q
Количеством движения системы будем называть векторную величину
, равную геометрической сумме количеств движения всех точек системы.
n
Q mk Vk
Q M VC
или
1
Теорема: Производная по времени от количества движения системы
свободных материальных точек равна геометрической сумме внешних сил.
В дифференциальной форме:
dQ n e
Fk
dt
1
Теорема: Изменение количества движения системы за некоторый промежуток
времени равно сумме импульсов, действующих на систему внешних сил за тот
же промежуток времени.
В интегральной форме: Q1 Q0
n
e
S
k
1

34.

При изучении движения твёрдого тела (системы тел) обычно используют
теорему о движении центра масс (хотя можно пользоваться и теоремой об
изменении количества движения системы).
При изучении движения непрерывной среды (жидкость, газ) понятие о
центре масс теряет смысл, поэтому используется только теорема об
изменении количества движения.
Следствие:
Если
F
е
k
0 , то Q1 Q0 const - закон сохранения количества
движения системы.
Примеры:
1) Отдача винтовки при выстреле: Пуля движется в одну сторону, а винтовка
– в другую с равным количеством движения.
2) Работа гребного винта: винт отбрасывает часть массы воды назад,
сообщая ей определённое количество движения; то же количество движения
сообщается и судну.
Q
не характеризует полностью движение тела (системы тел), т.к. если тело
вращается вокруг неподвижной оси, проходящей через центр масс тела, то
Q 0
Если тело совершает сложное движение, то Q не характеризует
вращательную часть его движения вокруг центра масс, а характеризует только
поступательное движение системы.

35.

4.4 Теорема об изменении главного
момента количеств движения системы
Главным моментом количеств движения системы (кинетическим
моментом системы) относительно центра О является векторная величина,
равная геометрической сумме моментов количества движения всех точек
системы относительно этого центра.
n
n
1
1
K 0 M O (mkVk ) (hk mk Vk )
Кинетический момент в проекциях на координатные
оси:
Главный момент количеств движения системы
характеризует вращательное движение системы.
n
K x M x (mkVk )
1
n
K y M y (mkVk )
1
n
K z M z (mkVk )
1
Частный случай: Тело вращается относительно
неподвижной оси Oz. Найдём кинетический момент
относительно этой оси.
M z (mkVk ) mk Vk hk mk k hk2

36.

Для всех точек системы:
n
n
1
1
K z M z (mkVk ) mk hk2
Kz J z
Таким образом, кинетический момент вращающегося тела
относительно оси вращения равен произведению момента инерции тела
относительно этой оси на угловую скорость тела.
Для осей x и y: K J
K J
x
xz
y
yz
Если ось вращения будет для точки О главной осью инерции тела, то:
KO K z J z
Теорема: Производная по времени от кинетического момента системы
свободных материальных точек равна сумме моментов всех внешних сил
(главному моменту всех внешних сил).
n
d KO
M O ( Fke )
dt
1
Эта теорема широко используется при изучении вращательного движения
тела; позволяет оценить вращательную компоненту плоскопараллельного
движения; позволяет исключить из рассмотрения все наперёд неизвестные
внутренние силы, а также те внешние силы, которые проходят через ось
вращения и оси, параллельные ей.

37.

Для осей, движущихся поступательно вместе с центром масс системы,
теорема моментов относительно центра масс сохраняет тот же вид, что и
относительно неподвижного центра.
n
d KC
M C ( Fke )
dt
1
4.5 Закон сохранения главного момента
количеств движения
n
Следствие: Если
e
M
(
F
O k ) 0 , то KO const
1
- закон сохранения кинетического момента системы.
Аналогично для кинетического момента относительно оси:
n
Если
M
e
(
F
z
k ) 0 то
K z const
1
Отсюда следует, что внутренние силы изменить главный момент количеств
движения не могут.
Если система вращается относительно неподвижной оси Oz, то
K z J z const
Для неизменяемой системы (абсолютно твёрдого тела) J z const , значит
const

38.

В случае изменяемой системы: некоторые точки удаляясь от оси вращения
увеличивают J , значит угловая скорость будет снижаться. И наоборот.
z
Таким образом, действием внутренних сил можно изменить угловую скорость
вращения всей системы.
4.5 Теорема об изменении кинетической
энергии системы
Кинетическая энергия системы:
1 т
Т mk Vk2
2 1
Кинетическая энергия не зависит от направления движения и не
характеризует изменение этого направления.
1
2
Т
M
V
Для поступательного движения:
пост
C
Для вращательного движения:
Общий случай:
Т вр
1
J C 2
2
1
Т ( M VC2 J C 2 )
2
2
Теорема: Дифференциал кинетической энергии системы свободных
материальных точек равен сумме элементарных работ всех внешних и
внутренних сил.
i
e
dT dA dA - в дифференциальной форме
k
k

39.

Или в интегральной форме:
Для точки и для неизменяемой системы с идеальными связями:
i
А
(
F
k) 0
5. Динамика твёрдого тела
Динамика поступательного движения твёрдого тела сводится к задачам
динамики точки.
5.1 Динамика вращательного движения
Пусть на твердое тело с неподвижной осью вращения
z действует система заданных сил F е 1 , F е 2 ,...F е n
R A и RB - реакции подшипников (наперед неизвестны).
Чтобы исключить из рассмотрения неизвестные
реакции, запишем теорему моментов относительно оси z:
n
d Kz
e
M z M z ( Fke )
dt
1

40.

M ze - вращающий момент.
!
d
Jz
J z M ze
dt
Так как
Kz J z
, то
– дифференциальное уравнение
вращательного движения твёрдого тела.
Уравнением целесообразно пользоваться, когда система состоит только из
одного вращающегося тела, если в системе кроме вращающегося тела есть и
другие движущиеся тела, то уравнение движения лучше составлять при
помощи методов аналитической механики.
5.2 Физический маятник
Физический маятник - твердое тело, которое может совершать колебания
вокруг неподвижной горизонтальной оси под действием силы тяжести.
M z M O P a sin
Уравнение вращательного движения:
d 2
J O 2 P a sin
dt
P a
k2
введём обозначение:
JO

41.

d 2
2
k
sin 0
2
dt
– дифференциальное уравнение физического маятника.
Это уравнение в обычных функциях не интегрируется.
Рассмотрим малые колебания маятника, когда
d
2
k
0
2
dt
C1 sin kt C2 cos kt
2
Тогда уравнение примет вид:
Решение уравнения:
при t =0:
0
sin
( 3 ...5 )
0
0 cos kt
Таким образом, малые колебания физического маятника являются
гармоническими.
Период колебаний:
TФ
JO
2
2
k
P a
Если специальными методами проинтегрировать диф. уравнение
d 2
2
k
sin 0 то
2
dt
J O 02
TФ 2
1
P a 16

42.

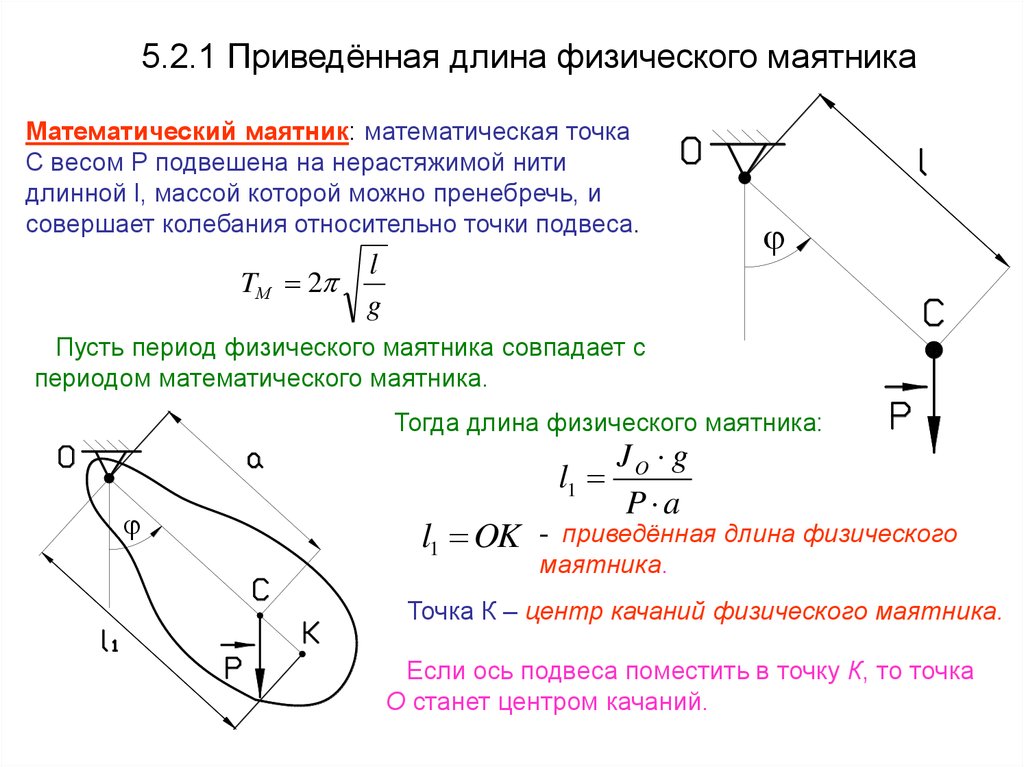
5.2.1 Приведённая длина физического маятника
Математический маятник: математическая точка
С весом Р подвешена на нерастяжимой нити
длинной l, массой которой можно пренебречь, и
совершает колебания относительно точки подвеса.
TМ 2
l
g
Пусть период физического маятника совпадает с
периодом математического маятника.
Тогда длина физического маятника:
l1 OK
JO g
l1
P a
- приведённая длина физического
маятника.
Точка К – центр качаний физического маятника.
Если ось подвеса поместить в точку К, то точка
О станет центром качаний.

43.

5.3 Плоскопараллельное движение
твёрдого тела.
Задачи динамики сильно упрощаются, если за полюс выбрать центр масс С.
C ( xC , yC , zC )
Тогда движение полюса найдём по теореме о движении центра масс:
М Wc Fke
А вращательное движение вокруг полюса опишется уравнением:
J C mC Fke
Или в проекциях на координатные оси для плоской системы сил:
d 2 xc
М 2 Fkxe
dt
d 2 yc
М 2 Fkye
dt
d 2
J C 2 mC Fke
dt
диф. уравнения плоскопараллельного
движения твёрдого тела.