КСП 12 Геометрия 10 класс 2 четверть двугранный угол

1. Углы в пространстве

2.

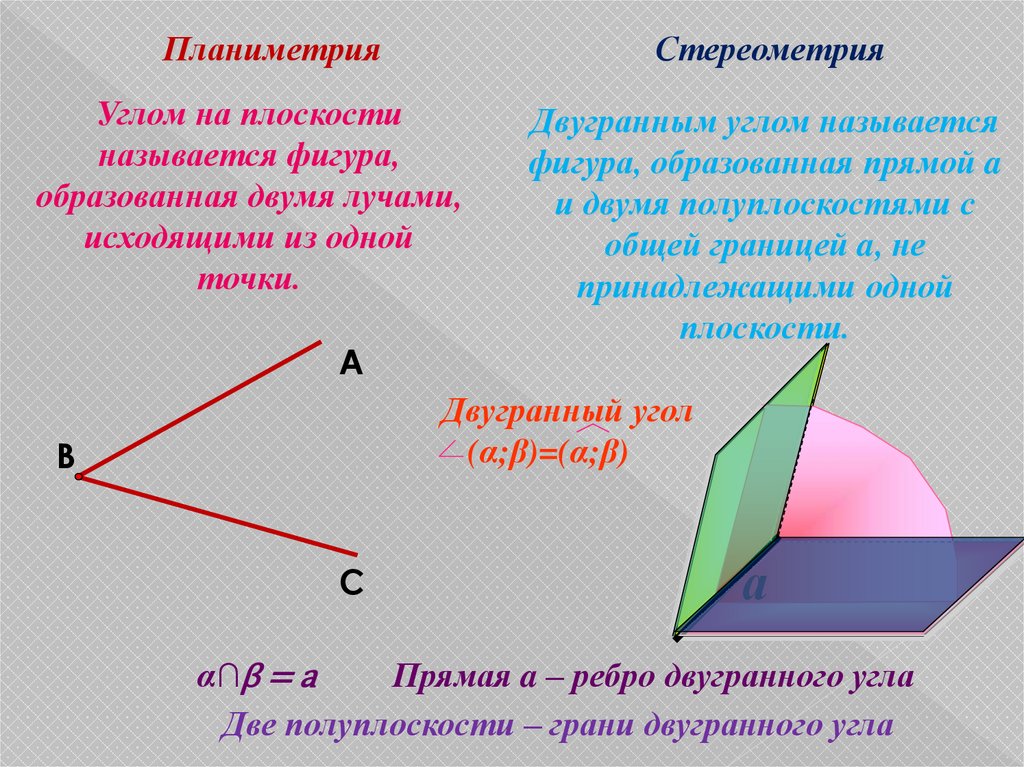
Планиметрия
Стереометрия
Углом на плоскости
называется фигура,
образованная двумя лучами,
исходящими из одной
точки.
Двугранным углом называется
фигура, образованная прямой a
и двумя полуплоскостями с
общей границей a, не
принадлежащими одной
плоскости.
А
Двугранный угол
(α;β)=(α;β)
В
С
а
α∩β = a
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла

3.

4.

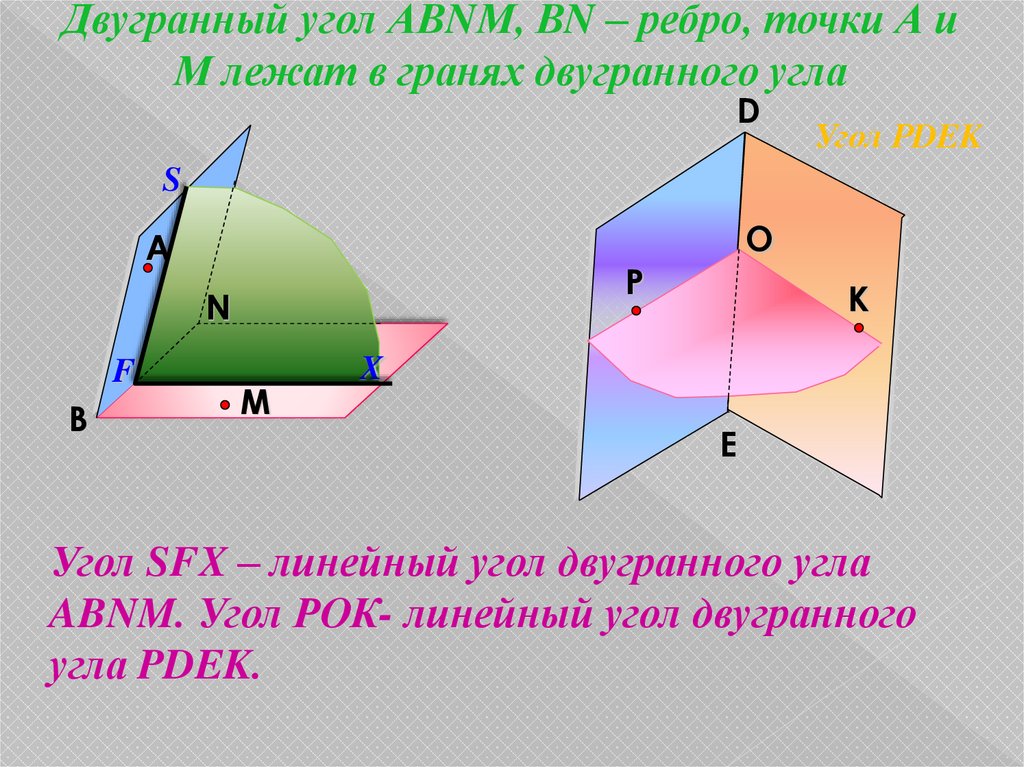
Двугранный угол АВNМ, ВN – ребро, точки А и
М лежат в гранях двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
M
К
X
E
Угол SFX – линейный угол двугранного угла
ABNM. Угол РОК- линейный угол двугранного
угла PDEK.

5.

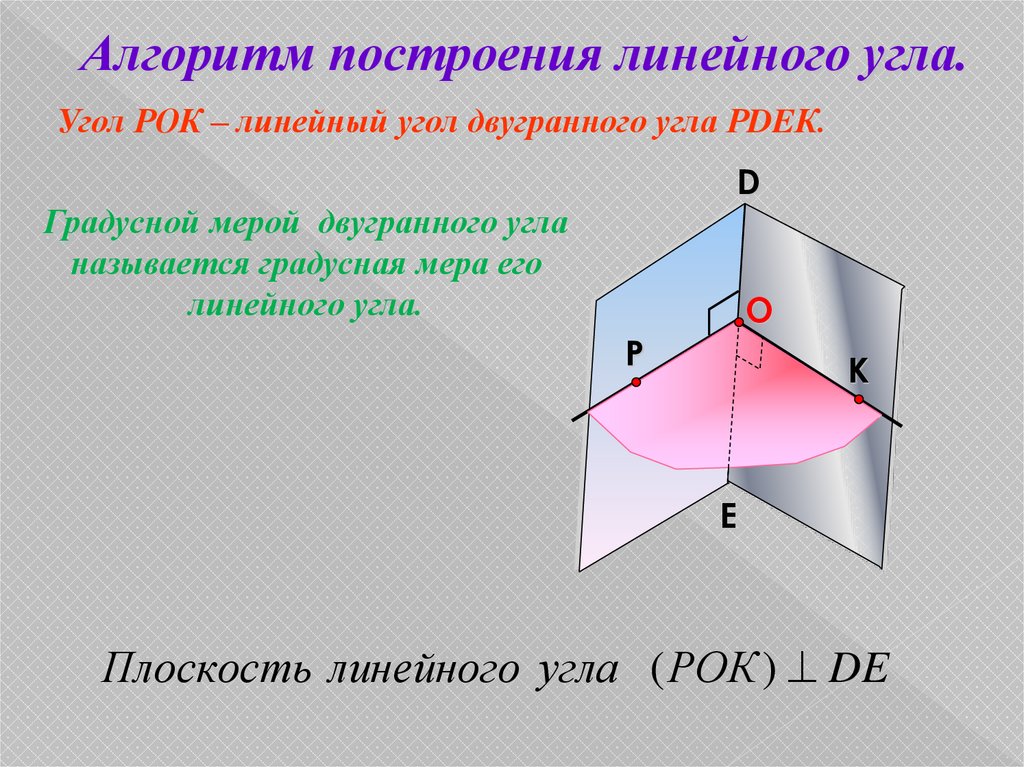
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла
называется градусная мера его
линейного угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE

6.

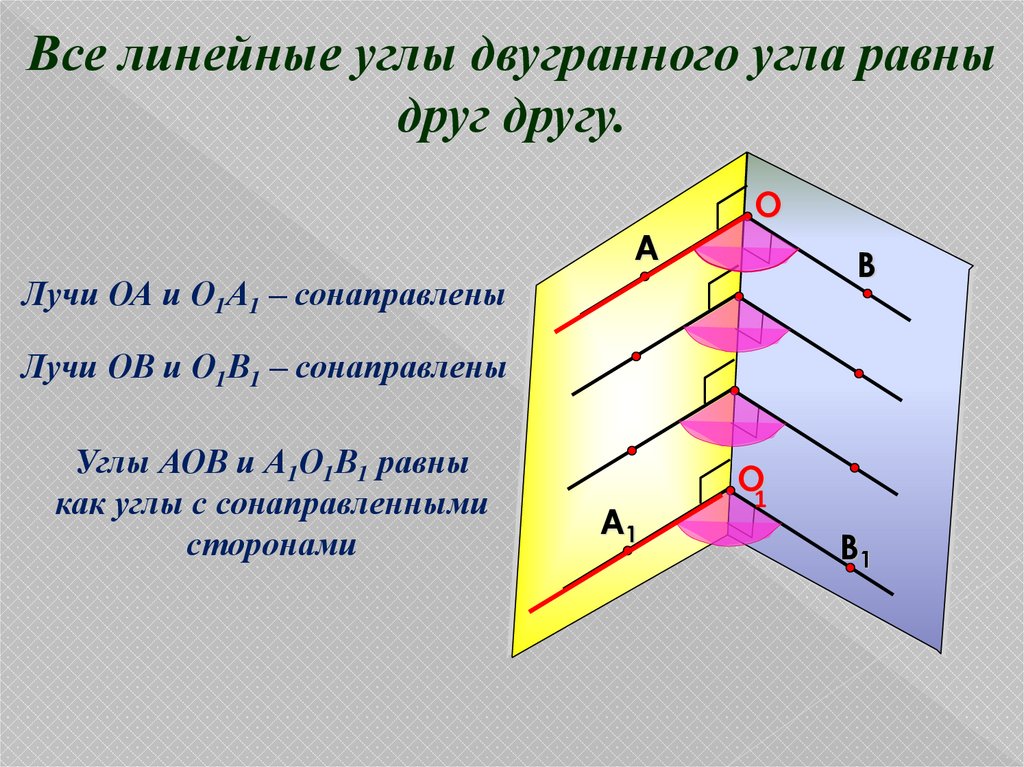
Все линейные углы двугранного угла равны
друг другу.
O
А
В
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны
как углы с сонаправленными
сторонами
А1
O1
В1

7.

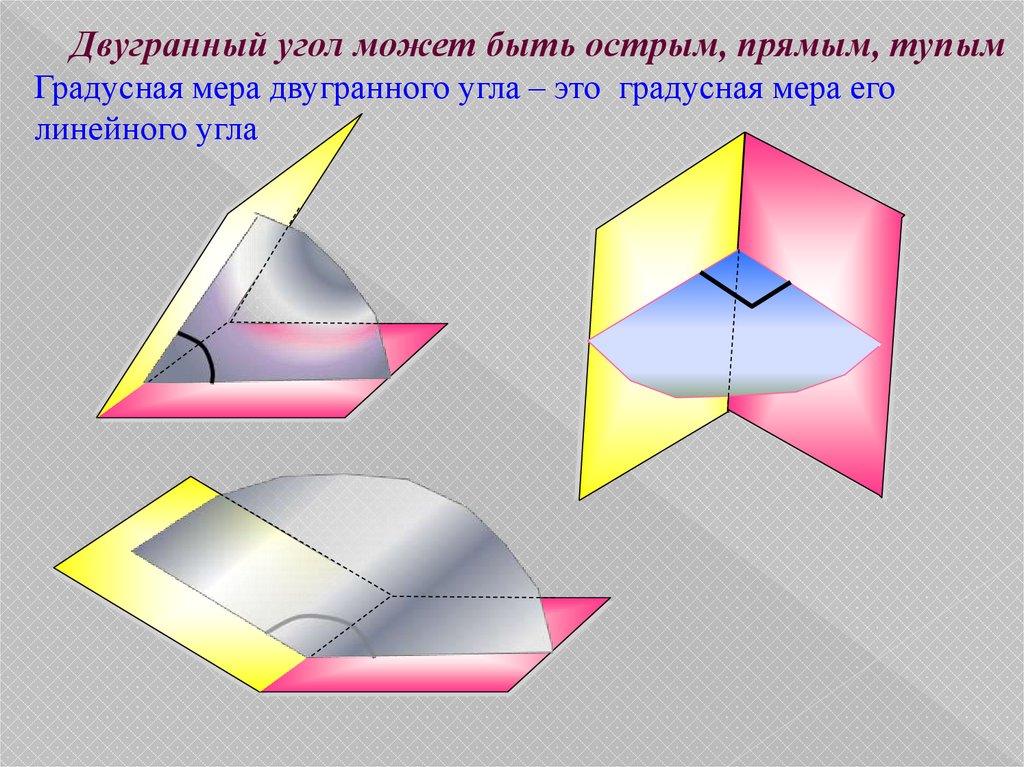
Двугранный угол может быть острым, прямым, тупым
Градусная мера двугранного угла – это градусная мера его
линейного угла

8.

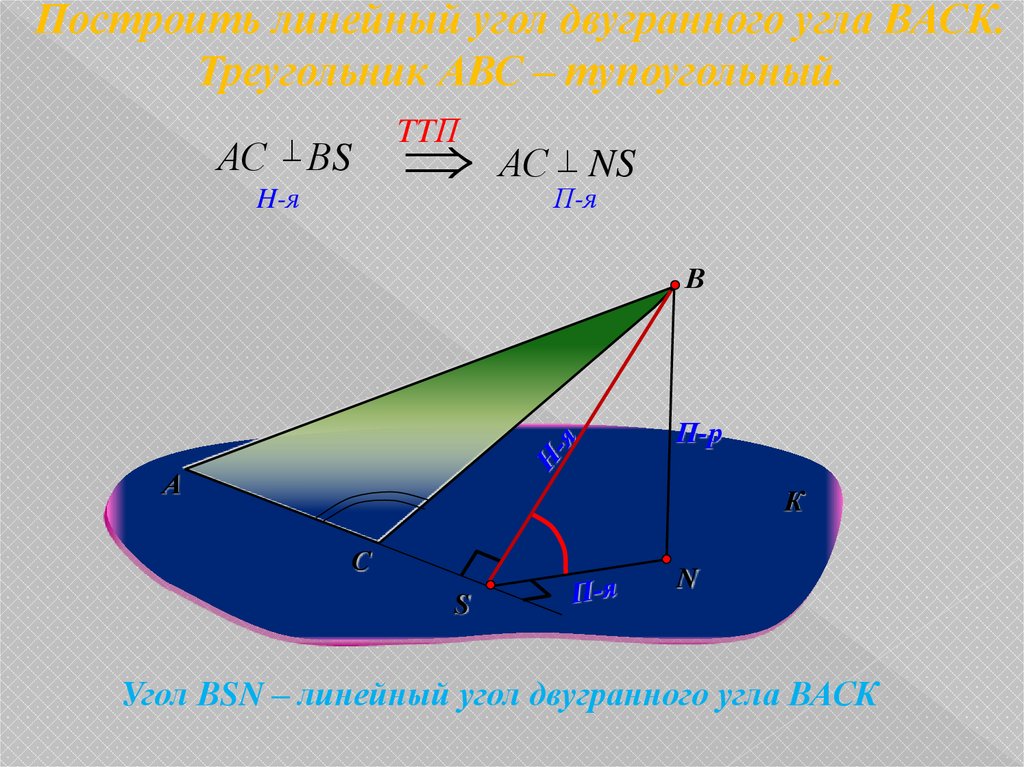
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
АС ВS
АС NS
TTП
П-я
H-я
В
П-р
А
К
С
S
N
Угол ВSN – линейный угол двугранного угла ВАСК

9.

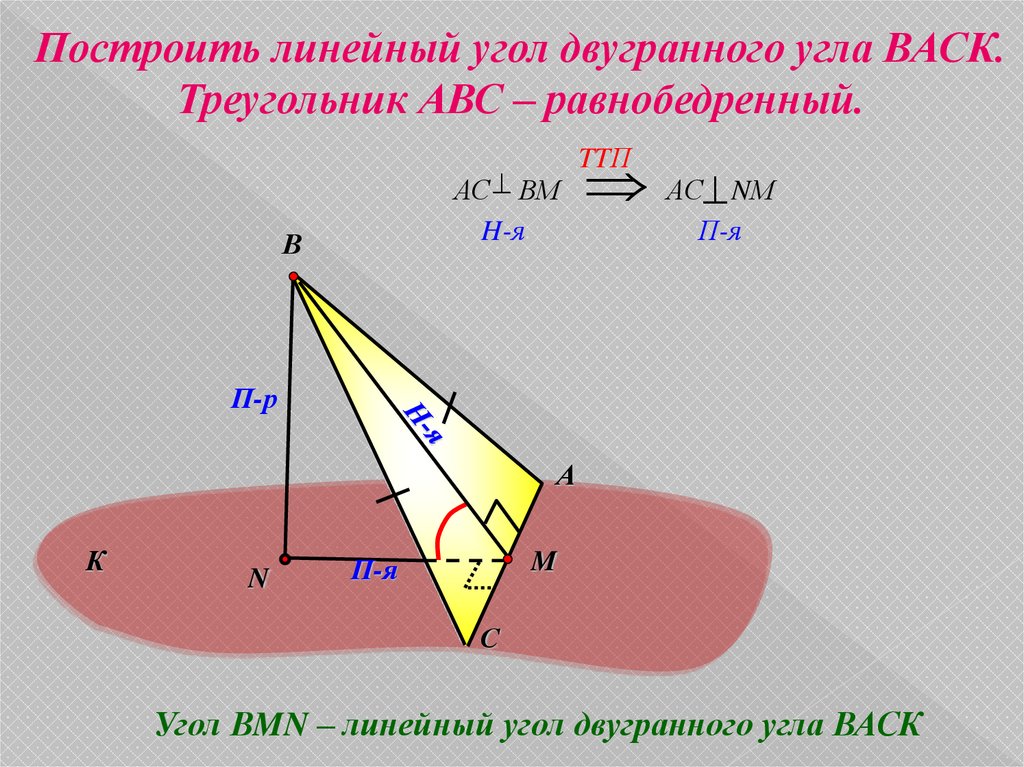
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
АС ВМ
H-я
В
АС NМ
TTП
П-я
П-р
А
К
N
M
П-я
С
Угол ВMN – линейный угол двугранного угла ВАСК

10.

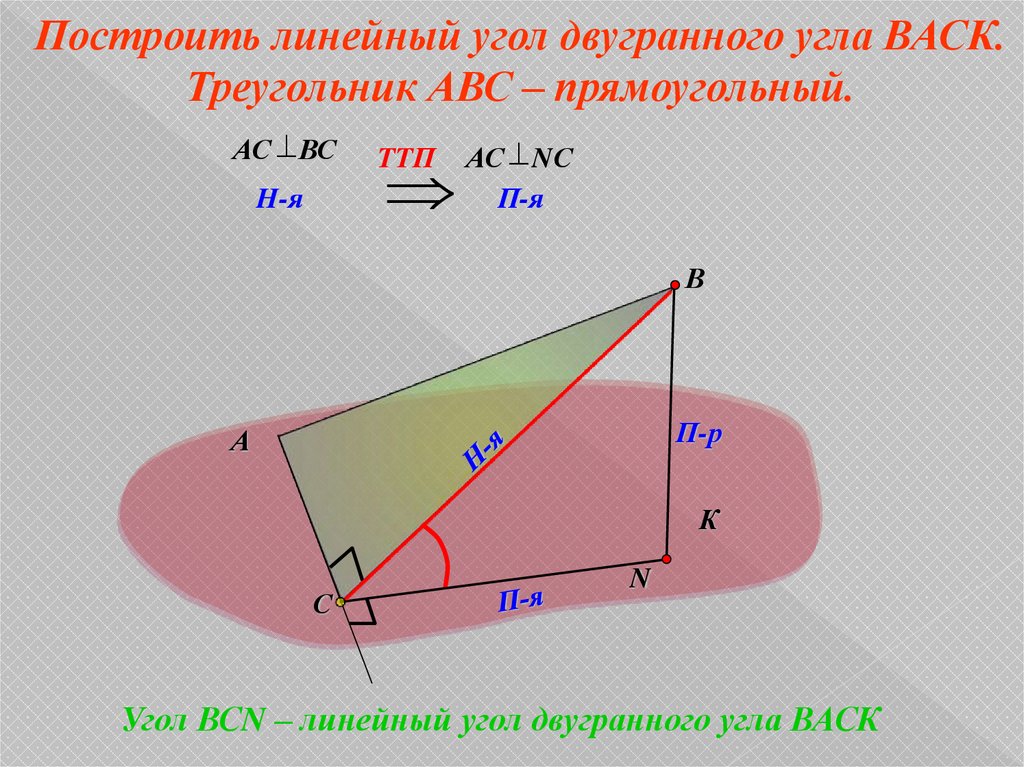
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС ВС
H-я
TTП
АС NС
П-я
В
П-р
А
К
С
N
Угол ВСN – линейный угол двугранного угла ВАСК

11.

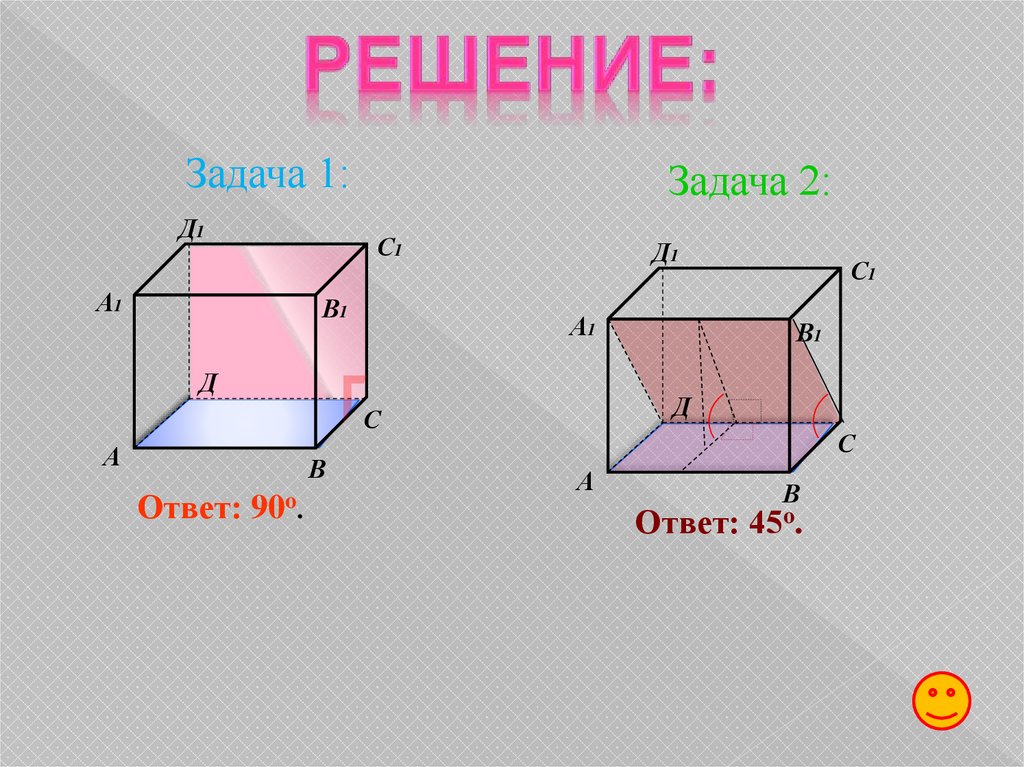
Первая группа
Задача 1
В кубе A…D1 найдите угол между плоскостями ABC и CDD1
Задача 2:
В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
Вторая группа
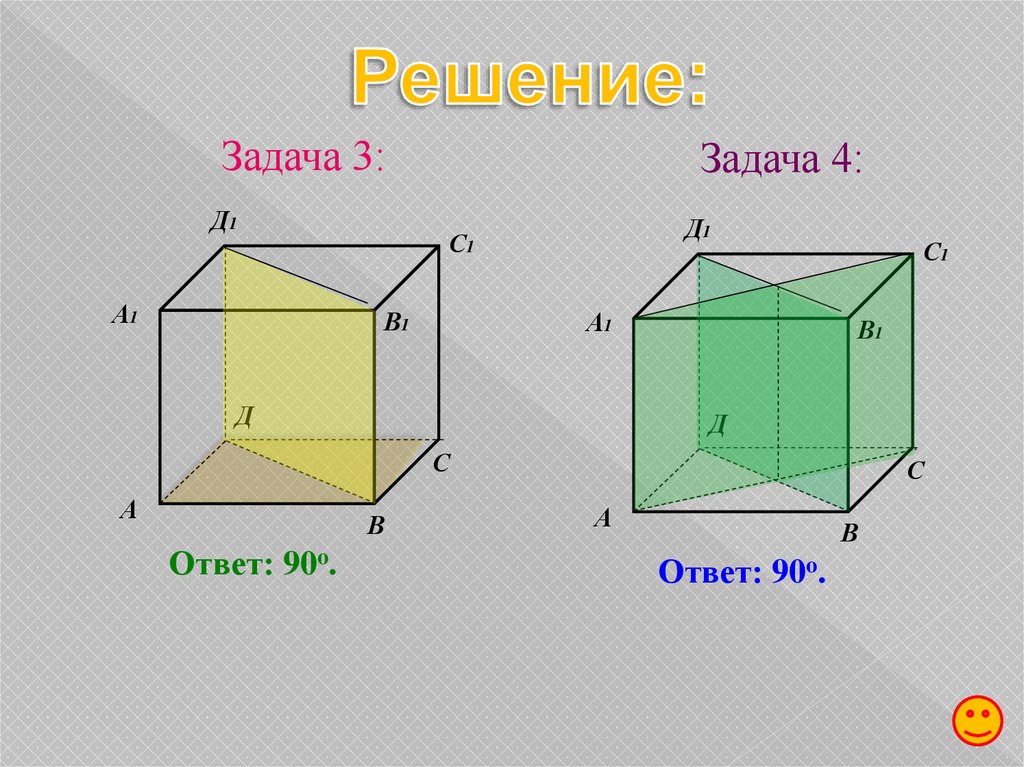
Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и
BDD1.

12.

Задача 1:
Д1
А1
Задача 2:
С1
В1
Д1
А1
Д
В
Ответ: 90o.
В1
Д
С
А
С1
С
А
В
Ответ: 45o.

13.

Задача 3:
Д1
А1
Задача 4:
Д1
С1
В1
А1
Д
С1
В1
Д
С
А
В
Ответ: 90o.
С
А
В
Ответ: 90o.

14.

Гипотенуза прямоугольного равнобедренного треугольника лежит в
плоскости