DCS_Lecture3_2023

1.

ЛЕКЦИЯ 3
2 Математические модели линейных непрерывных систем
2.1 Дифференциальные уравнения в форме Коши
2.2 Метод пространства состояний
2.3 Примеры описания систем в пространстве состояний
Цифровые системы управления

2.

2 Математические модели линейных непрерывных систем
2.1 Дифференциальные уравнения в форме Коши
Для одномерного объекта в общем
дифференциальное уравнение n-го порядка:
случае
может
быть
an y n an 1 y n 1 an 2 y n 2 ... a1 y a0 y bu
записано
(1)
Выполним замену переменных в этом уравнении следующим образом:
x1 y,
x x y ,
2
1
x2 x3 y ,
...
xn 1 xn y n 1.
(2)
и разрешим исходное уравнение относительно старшей производной
a
a
a b
a
y n n 1 y n 1 n 2 y n 2 ... 1 y 0 y u
an
an
an an
an
или
a
b
a
a
a
xn n 1 xn n 2 xn 1 ... 1 x2 0 x1 u
(3)
an
an
an an
an
Совокупность уравнений (2) и (3) представляют нормальную форму Коши
дифференциального уравнения (1).
Цифровые системы управления

3.

2.1 Дифференциальные уравнения в форме Коши
В общем виде полученная система представляется как
x Ax Bu
(4)
где
x1
0
A 0
0
a0
an
x2
x3
1
0
0
a
1
an
0
1
0
a
2
an
xn
0 y
0 y
1 y n 1
a
n 1 y n
an
есть матрица Фробениуса, а матрица
0
0
B
b
a
n
определяет влияние входного воздействия на состояние объекта.
Значение выходного сигнала y объекта определяется в общем случае как
состояние объекта x, так и значением входного воздействия u, поэтому получаем
y Cx Du
Цифровые системы управления

4.

2.2 Метод пространства состояний
Объекты управления в зависимости от степени сложности делятся по
числу выходных координат на одномерные и многомерные.
Описание одномерной системы с помощью передаточной функции:
Описание многомерной системы
u u1, u2 , ... , um T m-мерный вектор входных
переменных
x x1, x2 , ... , xn T n-мерный вектор переменных
состояния
y y1, y2 , ... , yk T k-мерный вектор наблюдаемых
Обобщенное представление
многосвязной системы управления
или выходных координат
Цифровые системы управления

5.

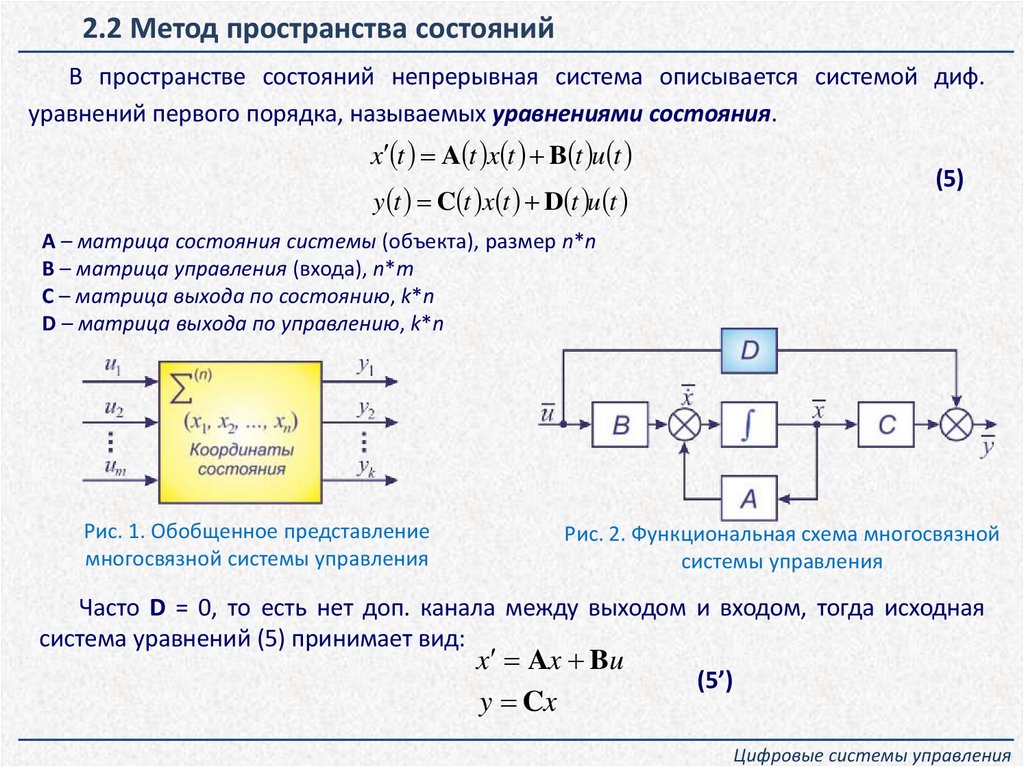
2.2 Метод пространства состояний
В пространстве состояний непрерывная система описывается системой диф.
уравнений первого порядка, называемых уравнениями состояния.
x t A t x t B t u t
(5)
y t C t x t D t u t
A – матрица состояния системы (объекта), размер n*n
B – матрица управления (входа), n*m
C – матрица выхода по состоянию, k*n
D – матрица выхода по управлению, k*n
Рис. 1. Обобщенное представление
многосвязной системы управления
Рис. 2. Функциональная схема многосвязной
системы управления
Часто D = 0, то есть нет доп. канала между выходом и входом, тогда исходная
система уравнений (5) принимает вид:
x Ax Bu
y Cx
(5’)
Цифровые системы управления

6.

2.2 Метод пространства состояний
Матрицы A, B, C могут быть переменными или постоянными, в
последнем случае модель системы называют стационарной или моделью с
постоянными параметрами.
Линейная система полностью задана, если заданы: ее матрицы A, B, C и
начальное состояние , что можно записать в виде:
n : A, B, C; x 0
(6)
Матричная передаточная функция системы имеет вид:
W p C pE A 1 B D
(7)
где E – единичная матрица.
Цифровые системы управления

7.

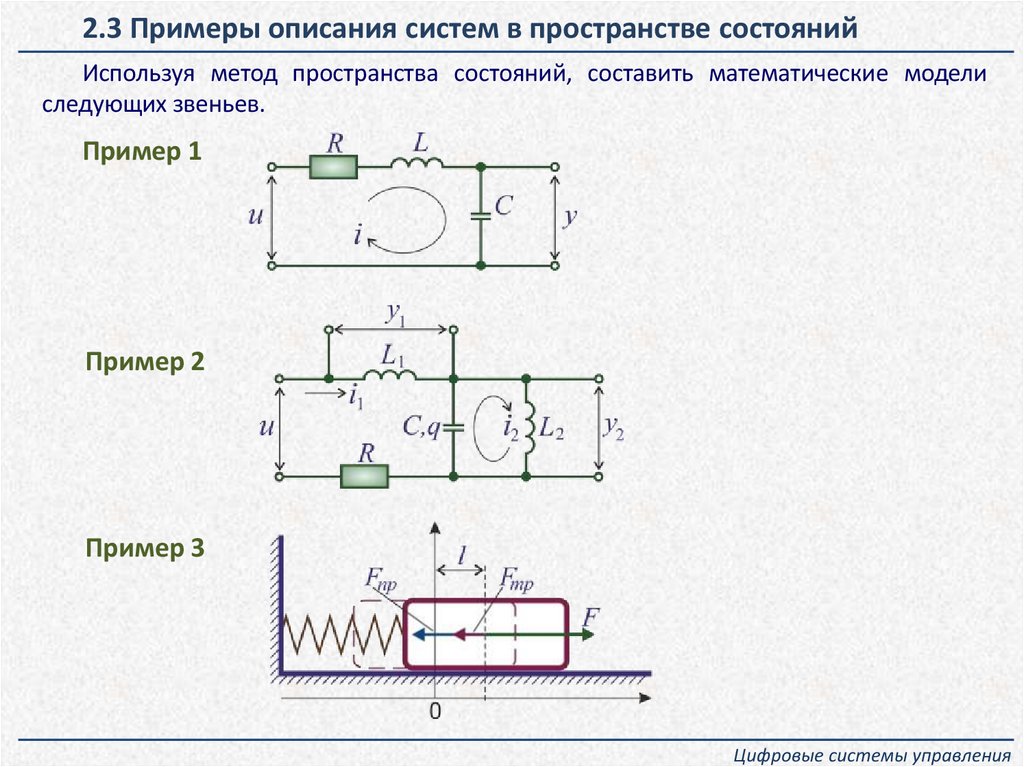
2.3 Примеры описания систем в пространстве состояний
Используя метод пространства состояний, составить математические модели
следующих звеньев.
Пример 1
Пример 2
Пример 3
Цифровые системы управления

8.

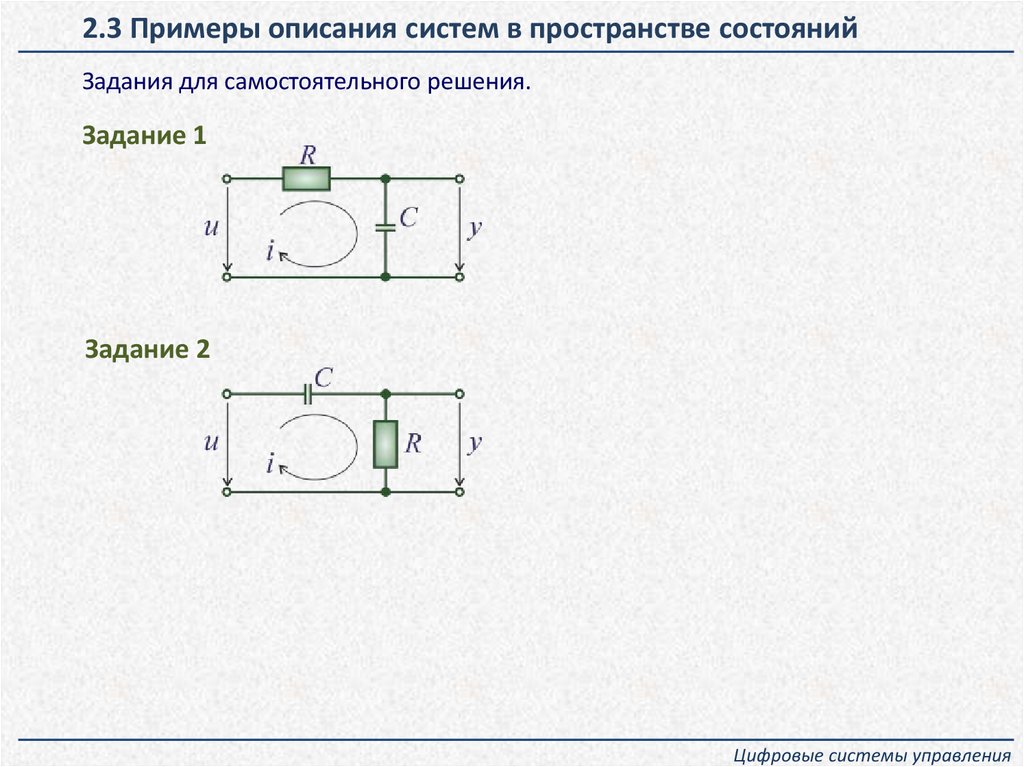
2.3 Примеры описания систем в пространстве состояний
Задания для самостоятельного решения.
Задание 1
Задание 2
Цифровые системы управления