Моделирование систем и процессов

1.

Моделирование систем и
процессов
Тема 6. Моделирование авиационных систем
Оператор многомерной линейной АС: представление оператора системой
линейных дифференциальных уравнений первого порядка, матричное
уравнение многомерной АС. Матричная передаточная функция.
Фундаментальная матрица многомерной АС. Многомерный интеграл
Дюамеля. Фундаментальная матрица и интеграл Дюамеля для
многомерной стационарной системы. Управляемость и наблюдаемость
систем. Общие положения о математическом моделирования статических
систем.
Лекция 7

2.

Знать:
• задачи исследования и оптимизации авиационных систем и
процессов эксплуатации авиационной техники, которые решаются
с помощью математического моделирования;
• методы моделирования сложных технических систем с учетом
особенностей структуры и функциональных задач;
• методику разработки моделей систем и процессов для решения
задач, возникающих при эксплуатации, а также научных и
инженерных исследованиях авиационных систем.

3.

Повторить самостоятельно:
Задачи анализа линейных САУ, решаемые на основе частотных
характеристик: определение устойчивости, оценка статической точности
статических и астатических систем. Оценка динамической точности,
построение переходного процесса и определение качества систем.
Задачи синтеза линейных систем частотными методами: построение
желаемой амплитудно-частотной характеристики системы, выбор и
определение корректирующего звена.
Модели линейных дискретных динамических систем. Определение
дискретной модели сигнала: виды модуляций, преобразование спектра
непрерывного сигнала при его прохождении через дискретную систему.
Передаточные функции дискретных моделей: Z- преобразование; Zпередаточные функции составляющих звеньев дискретных систем.
Передаточные функции разомкнутой и замкнутой системы. Определение
выходного сигнала. Временные характеристики дискретных систем.
Переходная функция. Устойчивость моделей дискретных систем. Частотные
характеристики дискретных систем. Синтез дискретных систем.
Дискретные корректирующие устройства.

4.

МНОГОМЕРНЫЕ АС
Многомерной называется АС с двумя и более выходными сигналами.
Линейной нестационарной системой называется такая система,
операторы которой представляются линейными дифференциальными
уравнениями с переменными коэффициентами.
an(t) y(n)(t) + an-1(t) y(n-1)(t) + a0(t) y(t) = bm(t) x(m)(t) + bm-1(t) x(m-1)(t) + b0(t) x(t)
y(t) выходной сигнал; x(t) входной сигнал;
ai(t), (i=
1, n
) и bi(t), (i= 1, m ) заданные кусочно-непрерывные функции.
ai(t) и bi(t) называются коэффициентами уравнения или параметрами АС
Если в момент времени ti коэффициент an(ti)=0, то эта точка (ti) является
особенностью уравнения
Предполагается, что уравнение лишено особенностей, то есть
an(t) 0.

5.

Разделим уравнение на старший коэффициент an(t)
y(n)(t) + n-1(t) y(n-1)(t) + 0(t) y(t) = m(t) x(m)(t) + m-1(t) x(m-1)(t) + 0(t) x(t)
i ( t )
ai ( t )
;
an ( t )
i ( t )
bi ( t )
.
an ( t )
Для решения необходимо задать начальные условия
t t0 , y t0 y0 , y(1) t0 y0( 1 ) , , y(n-1) t0 y0( n 1 )
вычислить правую часть уравнения
На ЦВМ можно вычислить правую часть уравнения, если функция x(t)
является n раз дифференцируема в каждый момент времени t
если входной сигнал имеет вид ступенчатой функции, то эта функция
не имеет производной в момент времени
Таким образом, уравнение не
приспособлено в прямом виде для
моделирования на ЦВМ.

6.

Для численного решения уравнения линейной нестационарной АС на ЦВМ
необходимо преобразовать его к форме Коши, то есть к системе n
дифференциальных уравнений 1-го порядка. В правых частях этих искомых
уравнений должны отсутствовать производные от входного сигнала.
Поставленная задача решается, если m n, то есть если выполняется условие
технической реализуемости системы.
y ( n ) ( t ) n 1 ( t ) y ( n 1 ) ( t ) 0 ( t ) y( t ) m ( t )x( m ) ( t ) 0 ( t )x( t )
Вводим новые переменные
y1 ( t ) y( t ) F0 ( t )x( t )
y2 ( t ) y1( 1 ) ( t ) F1 ( t )x( t )
y1( 1 ) ( t ) y 2 ( t ) F1 ( t )x( t ),
…
(1)
y 2 ( t ) y 3 ( t ) F2 ( t )x( t ),
y ( 1 ) ( t ) y ( t ) F ( t )x( t ),
n
n 1
n( 11)
y n ( t ) 0 ( t ) y1 ( t ) 1 ( t ) y 2 ( t ) n 1 ( t ) y n ( t ) Fn ( t )x( t ).
Решаем систему n дифференциальных уравнений 1-го порядка
Находим выходной сигнал
Как определить
y (t ) y1 (t ) F0 (t ) x(t ) y1 (t ) 0 (t ) x(t ) .
F0(t), F1(t), F2(t) …
???

7.

F0(t), F1(t), F2(t) … должны удовлетворять следующим равенствам:
0 t F0 t
1 t 2 F0( 1 ) t F1 t 1 t F0 t ,
2 t F0( 2) t F1(1) t 1 t F0(1) t 1 t F1 t 0 t F0 t F2 t
…
Если в операторе отсутствуют производные от входного сигнала x(t):
y ( n ) ( t ) n 1 ( t ) y ( n 1 ) ( t ) + 0 ( t ) y( t ) 0( t ) x( t )
y1( 1 ) ( t ) y 2 ( t ),
(1)
y 2 ( t ) y3 ( t ),
y n( 1 ) ( t ) 0 ( t ) y1 ( t ) 1 ( t ) y 2 ( t ) n 1 ( t ) y n ( t ) 0 ( t )x( t ).
y( t ) y1 ( t ).

8.

Матричное уравнение многомерной АС
y1( 1 ) ( t ) a11 ( t ) y1 ( t ) a12 ( t ) y 2 ( t ) a1n ( t ) y n ( t ) x1 ( t ),
(1)
y 2 ( t ) a21 ( t ) y1 ( t ) a22 ( t ) y 2 ( t ) a2 n ( t ) y n ( t ) x2 ( t ),
(1)
y
n ( t ) an1 ( t ) y1 ( t ) an 2 ( t ) y 2 ( t ) ann ( t ) y n ( t ) xn ( t ).
x1 ( t ), , xn ( t )
- входные сигналы
y1 ( t ), , yn ( t )
- выходные сигналы
aij ( t ) , i = 1,n , j = 1,n
- заданные функции времени,
коэффициенты (параметры) системы

9.

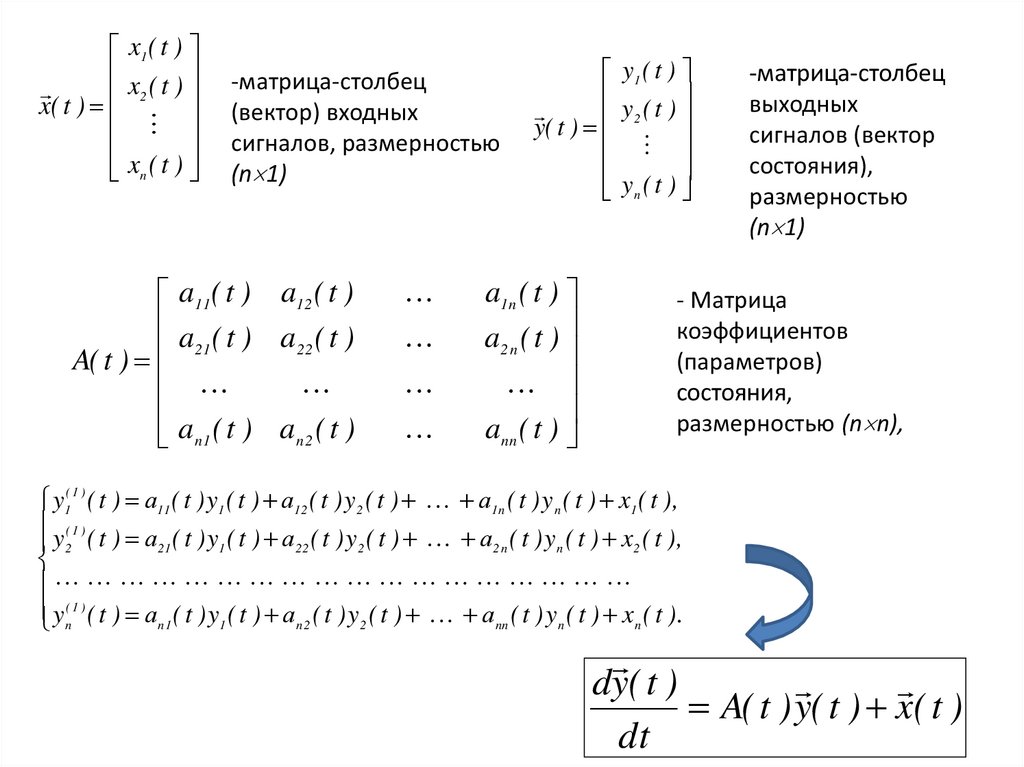
x1 ( t )
x (t )
x( t ) 2
xn ( t )
-матрица-столбец
(вектор) входных
сигналов, размерностью
(n 1)
a11 ( t ) a12 ( t )
a (t ) a (t )
22
A( t ) 21
an1 ( t ) an 2 ( t )
y1 ( t )
y (t )
y( t ) 2
y
(
t
)
n
a1n ( t )
a2 n ( t )
ann ( t )
-матрица-столбец
выходных
сигналов (вектор
состояния),
размерностью
(n 1)
- Матрица
коэффициентов
(параметров)
состояния,
размерностью (n n),
y1( 1 ) ( t ) a11 ( t ) y1 ( t ) a12 ( t ) y 2 ( t ) a1n ( t ) y n ( t ) x1 ( t ),
(1)
y 2 ( t ) a21 ( t ) y1 ( t ) a22 ( t ) y 2 ( t ) a2 n ( t ) y n ( t ) x2 ( t ),
y n( 1 ) ( t ) an1 ( t ) y1 ( t ) an 2 ( t ) y 2 ( t ) ann ( t ) y n ( t ) xn ( t ).
dy( t )
A( t ) y( t ) x( t )
dt

10.

Матричная передаточная функция
dy( t )
A( t ) y( t ) x( t )
dt
pY ( p ) AY ( p ) X ( p )
так как Y ( p ) EY ( p )
( Ep A )Y ( p ) X ( p )
единичная матрица
характеристическая матрица матрицы А
det( Ep A ) характеристический определитель матрицы А
или характеристический полином системы
det( Ep A ) an p n an 1 p n 1 a1 p a0
1
Y ( p ) ( Ep A ) X ( p ) Ф( p ) X ( p )
1
Ф( p ) ( Ep A )
S( p )
Ф( p )
det( Ep A )
S(p) является присоединенной матрицей относительно характеристической
матрицы системы ( Ep A )

11.

Присоединенной матрицей относительно матрицы А называется
матрица, составленная из алгебраических дополнений транспонированной
матрицы
A11
A12
~
A
A1n
A21
A22
A2 n
An1
An 2
Ann
Аij алгебраические дополнения матрицы
AT
Алгебраическим дополнением Аij элемента aij квадратной матрицы
А(n,n) называется определитель, составленный из элементов
квадратной матрицы после вычеркивания i-й строки и j-го столбца и
умноженный на - 1 i j

12.

Фундаментальная матрица многомерной АС
Для одномерной АС ее динамические свойства определяются передаточной
функцией. Знание фундаментальной матрицы позволяет определить
реакцию многомерной системы на произвольный входной сигнал.
Если входной сигнал многомерной нестационарной системы равен нулю
dy( t )
A( t ) y( t ) x( t )
dt
y( t ) A( t ) y( t )
матричное линейное однородное
дифференциальное уравнение 1-го
порядка, которое описывает “внутреннее,
свободное” или “собственное” движение
многомерной системы
Обозначим время фиксации начальных условий через t0 и
рассмотрим n вариантов единичных начальных условий:
T
T
T
y1 ( ) 1 0 0 , y2 ( ) 0 1 0 0 , , yn ( ) 0 0 1 .

13.

Для n вариантов начальных условий будет соответственно n вариантов
решений системы
g 11 ( t , )
g 12 ( t , )
g 1n ( t , )
g ( t , )
g ( t , )
g ( t , )
21
22
, g 2 ( t , )
, , g n ( t , ) 2n
g 1 ( t , )
g
(
t
,
)
g
(
t
,
)
g
(
t
,
)
n1
n2
nn
Здесь t текущее время определения значения координаты собственного
движения системы; момент фиксации начальных условий
g i ( t , ) i -й вектор выходных сигналов системы, если в момент t0
зафиксирован i-й вариант начальных условий
T
yi ( ) 0 0 1 0 , то есть
y1 ( ) 0 , y 2 ( ) 0 , , yi ( ) 1, yi 1 ( ) 0 , , y n ( ) 0 .
g ij ( t , ) значение выходного сигнала yi ( t ) в момент времени t, если в
момент времени t0 зафиксирован j-й вариант начальных
условий
первый индекс i определяет номер выхода системы в момент времени t, а второй
индекс j определяет на каком выходе устанавливается ненулевое начальное
условие (единица) в момент времени .

14.

g i ( t , ) (i = 1,n )
- решения
y( t ) A( t ) y( t )
g i ( t , ) A( t )g i ( t , ) , i = 1,n
g 11 ( t , ) g 12 ( t , )
g ( t , ) g ( t , )
22
Ф( t , ) g 1 ( t , ) g 2 ( t , ) g n ( t , ) 21
g n1 ( t , ) g n2 ( t , )
Весовые функции
системы.
g 1n ( t , )
g 2n ( t , )
g nn ( t , )
Совокупность всех n решений
Ф ( t , ) A( t )Ф( t , )
1 0
0 1
Для t= каждый столбец матрицы
Ф( t ,t ) Ф( , )
Ф(t, ) есть начальные условия
0 0
Фундаментальная матрица описывает внутреннее
движение системы, или ее переходные процессы
0
0
E
1

15.

При интегрировании параметр
фиксируется.
Ф ( t , ) A( t )Ф( t , )
1 0
0 1
Ф( t ,t ) Ф( , )
0 0
0
0
E
1
После этого определяются начальные
условия для данного .
И далее система интегрируется по
времени t справа и слева от .
Многомерный интеграл Дюамеля
Для многомерной нестационарной системы с оператором
y( t ) A( t ) y( t ) x( t )
A(t) известная матрица
и фундаментальной матрицей
Ф ( t , ) A( t )Ф( t , ), Ф( t ,t ) Ф( , ) E
t
y( t ) Ф( t ,t0 ) y0 Ф( t , )x( )d
t0
t0 момент включения
системы
T
T
y0 y( t0 ) y1 ( t0 ) y2 ( t0 ) yn ( t0 ) y10 y20 yn0 НУ

16.

Фундаментальная матрица и интеграл Дюамеля для
многомерной стационарной систем
dy
Ay( t ) x( t )
dt
a11
a
A 21
an 1
a12
a22
an 2
a1n
a2 n
ann
Фундаментальная матрица остается постоянной при сдвиге ее аргументов
на одно и то же (произвольное) число 1
Ф( t , ) Ф( t 1 , 1 )
т.е. оператор не зависит от момента включения системы
Если входные сигналы равны нулю и начальные условия зафиксированы,
то выходные сигналы определяются только временем, прошедшим от
момента включения систем, т.е. фундаментальная матрица стационарной
системы является функцией одного аргумента
~
dФ( t )
~
AФ( t )
dt
~
~
Ф( t t ) Ф( 0 ) E

17.

A t A 2 t 2 A3 t 3
~
Ф( t ) E
1!
2!
3!
2
3
x
x
x
ex 1
1! 2! 3!
~
Ф( t ) e At
~
dФ( t )
~
AФ( t )
dt
~
~
Ф( t t ) Ф( 0 ) E
~
~
pФ( p ) E A Ф( p )
~
( Ep A )Ф( p ) E ,
t
~
~
y( t ) Ф( t t0 ) y0 Ф( t ) x( )d
~
1
Ф( t ) L 1 Ep A
многомерный интеграл Дюамеля
t0
t
y( t ) e A( t t0 ) y0 e A( t ) x( )d
t0
Формула Коши

18.

Понятие управляемости и наблюдаемости АС
Рассмотрим линейный стационарный объект
вектор координат состояния
y Ay Bu
заданные числовые
матрицы коэффициентов
системы
вектор управления
a11 ... a1n
A ... ... ... ,
an1 ... ann
b 11 ... b 1m
B = ... ... ...
b n1 ... b nm
Многомерная система называется управляемой,
если она может быть
переведена из любого начального состояния y 0 в любое другое конечное
состояние y k
за конечный интервал времени
под воздействием кусочно
непрерывного управляющего воздействия u ( t )
y 1 ( t ) a11 0 y 1 ( t ) b 11 b 1m u 1 ( t )
y
(
t
)
0
a
y
(
t
)
b
b
u
(
t
)
n1
n
nn
nm
m
n
Если элементы i-й строки матрицы B равны нулю, то соответствующее этой
i (t ) aii y i (t )
строке дифференциальное уравнение y
Координата может изменяться только при наличии ненулевых НУ. Говорят, что система
в этом случае является неуправляемой.

19.

Для того чтобы система была управляемой, необходимо, чтобы
хотя бы один из элементов каждой строки матрицы В был
отличен от нуля.
Необходимое и достаточное условие управляемости
системы определяется равенством
R M R B, AB, A 2 B , ... , А n -1B n ,
или
rank M = n
M B, AB, A 2 B, ... , A n-1 B
блочная матрица, имеющая n строк и
n×m столбцов

20.

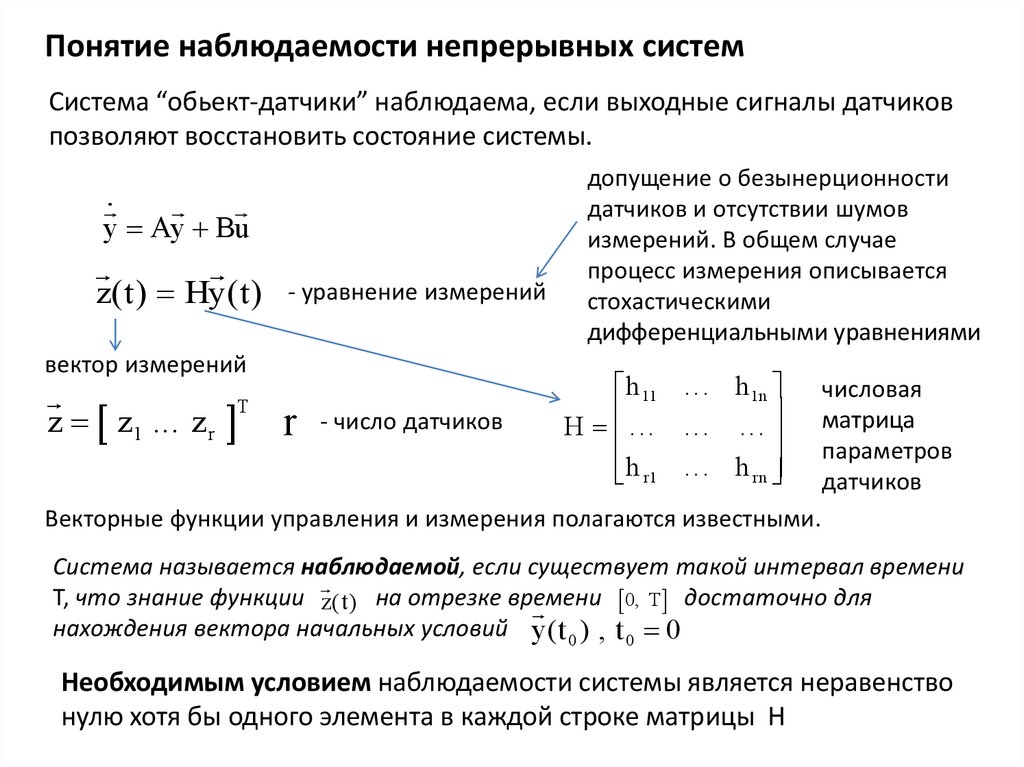
Понятие наблюдаемости непрерывных систем
Система “обьект-датчики” наблюдаема, если выходные сигналы датчиков
позволяют восстановить состояние системы.
y Ay Bu
z( t ) Hy( t )
- уравнение измерений
вектор измерений
T
z z1 ... z r
r - число датчиков
допущение о безынерционности
датчиков и отсутствии шумов
измерений. В общем случае
процесс измерения описывается
стохастическими
дифференциальными уравнениями
h 11 ... h 1n
H ... ... ...
h r1 ... h rn
числовая
матрица
параметров
датчиков
Векторные функции управления и измерения полагаются известными.
Система называется наблюдаемой, если существует такой интервал времени
Т, что знание функции z( t ) на отрезке времени
0, Т достаточно для
нахождения вектора начальных условий y( t 0 ) , t 0 0
Необходимым условием наблюдаемости системы является неравенство
нулю хотя бы одного элемента в каждой строке матрицы H

21.

Необходимое и достаточное условие наблюдаемости многомерной
системы
R N R H T , A T H T , A T
или
rank N = n
2
H n ,
H T , ... , A T
n-1
T

22.

Общие положения о математическом моделирования
статических систем
Режим функционирования технической системы определяется
характером внешних возмущающих и управляющих воздействий.
Различают статические и динамические режимы.
Динамическим называется режим, в котором состояние
системы неустановившееся. Он обусловлен изменением во
времени внешних воздействий, вызывающих возникновение
переходных процессов системы, при которых изменяются ее
фазовые координаты.
При постоянных воздействиях система находится в
установившемся равновесном состоянии. Ее фазовые
координаты при этом постоянны. Такой режим
функционирования системы называется статическим.
Для статического режима характерна неизменность реакций взаимодействия всех
элементов технической системы и реакций внешней среды. В электрической системе
сохраняется постоянство токов и напряжений во всех элементах электрической цепи

23.

Постановка задач анализа статических состояний
Существует несколько подходов к постановке и решению задач анализа
статических состояний технических систем. Они различаются используемыми
математическими моделями и методами решения систем уравнений.
1. Математическая модель статического состояния
технического объекта представляет собой систему линейных
или нелинейных алгебраических уравнений вида
где V — вектор фазовых координат технической системы.
2. Статическое состояние системы определено на основе
исходной математической модели технической системы, т.е.
системы обыкновенных дифференциальных уравнений
Численное решение этих уравнений при неизменных внешних воздействиях
через конечный отрезок времени tK приводит к стационарной точке V* , в
которой dV/dt = 0 . Координаты этой точки и будут соответствовать
искомому решению.

24.

3. Представить задачу анализа как экстремальную. Для этого
необходимо сформировать целевую функцию, имеющую
минимум в точке решения задачи V*. В качестве целевой
функции может
быть принята, например, скалярная
функция Ф(V ) , равная сумме квадратов невязок Fi (V )
системы уравнений
*
F (V ), F (V ) — скалярное
где n — порядок системы уравнений;
произведение векторов F (V ) , F (V )
Невязка Fi (V ) возникает, если в i-e уравнение системы
подставить произвольный вектор фазовых координат V,
отличающийся от вектора V* . В этом случае уравнения не
удовлетворяются и возникает вектор невязок.
Определение фазовых координат стационарной точки производится с
применением методов поиска минимума целевой функции. При этом
находится приближенное решение оптимизационной задачи.