Презентация. Прямоугольная система координат в пространстве

1. Прямоугольная система координат в пространстве.

ПРЯМОУГОЛЬНАЯ СИСТЕМА
КООРДИНАТ В ПРОСТРАНСТВЕ.

2.

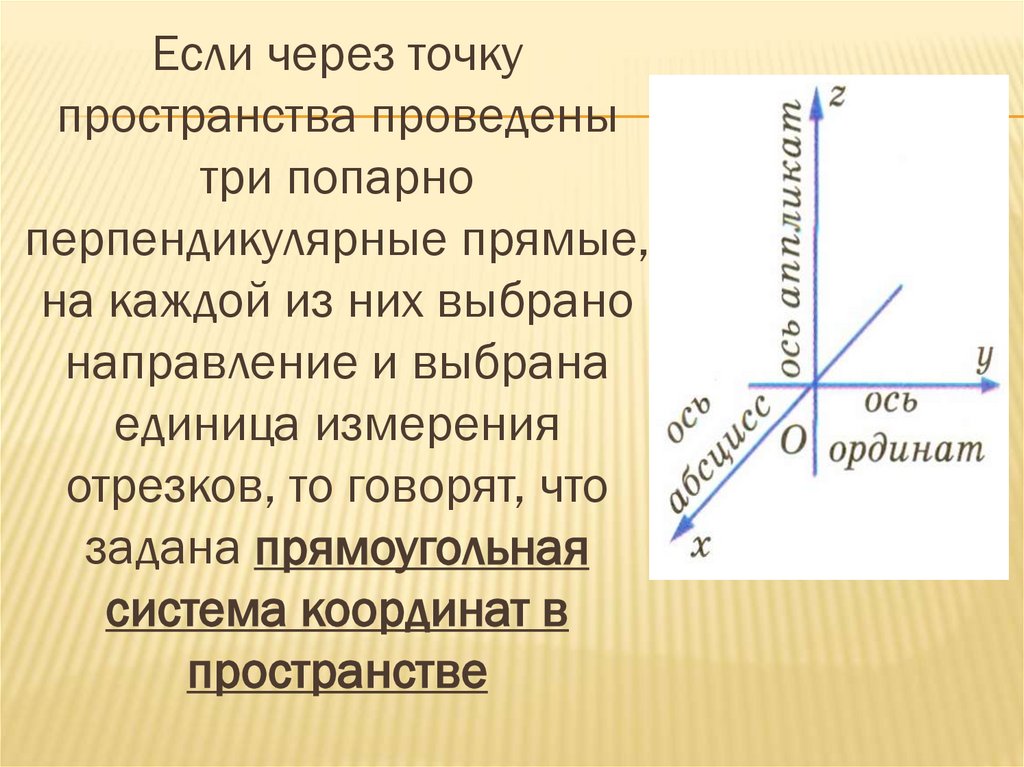
Если через точку
пространства проведены
три попарно
перпендикулярные прямые,
на каждой из них выбрано
направление и выбрана
единица измерения
отрезков, то говорят, что
задана прямоугольная
система координат в
пространстве

3.

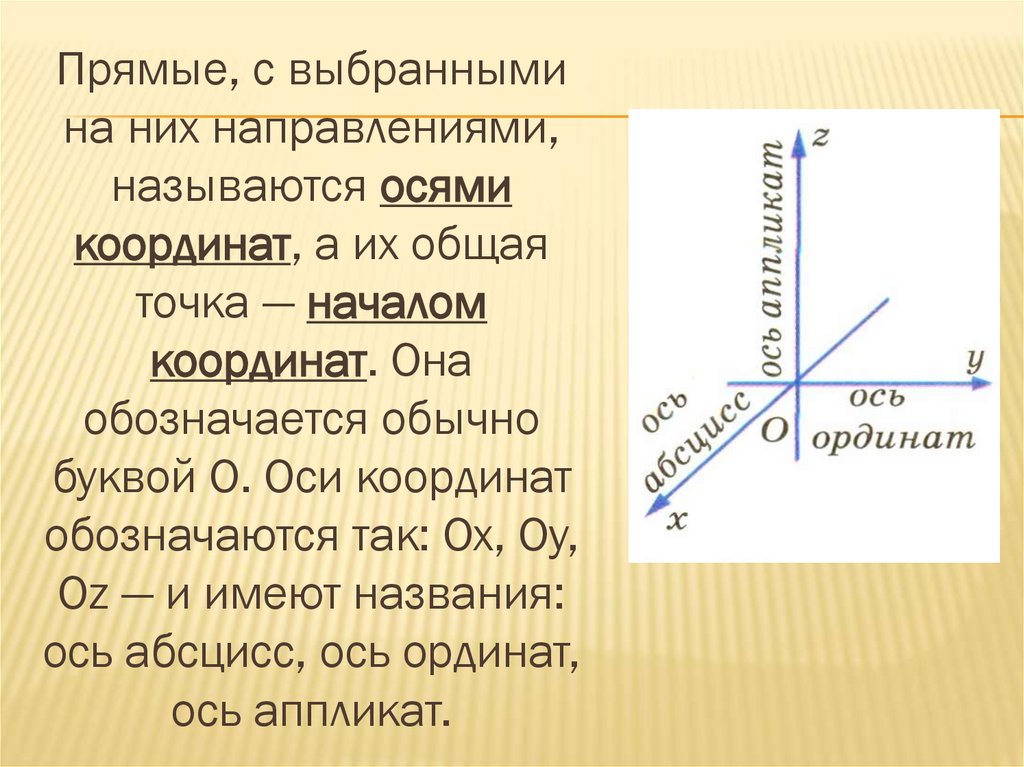
Прямые, с выбранными
на них направлениями,
называются осями
координат, а их общая
точка — началом
координат. Она
обозначается обычно
буквой О. Оси координат
обозначаются так: Ох, Оу,
Оz — и имеют названия:
ось абсцисс, ось ординат,
ось аппликат.

4.

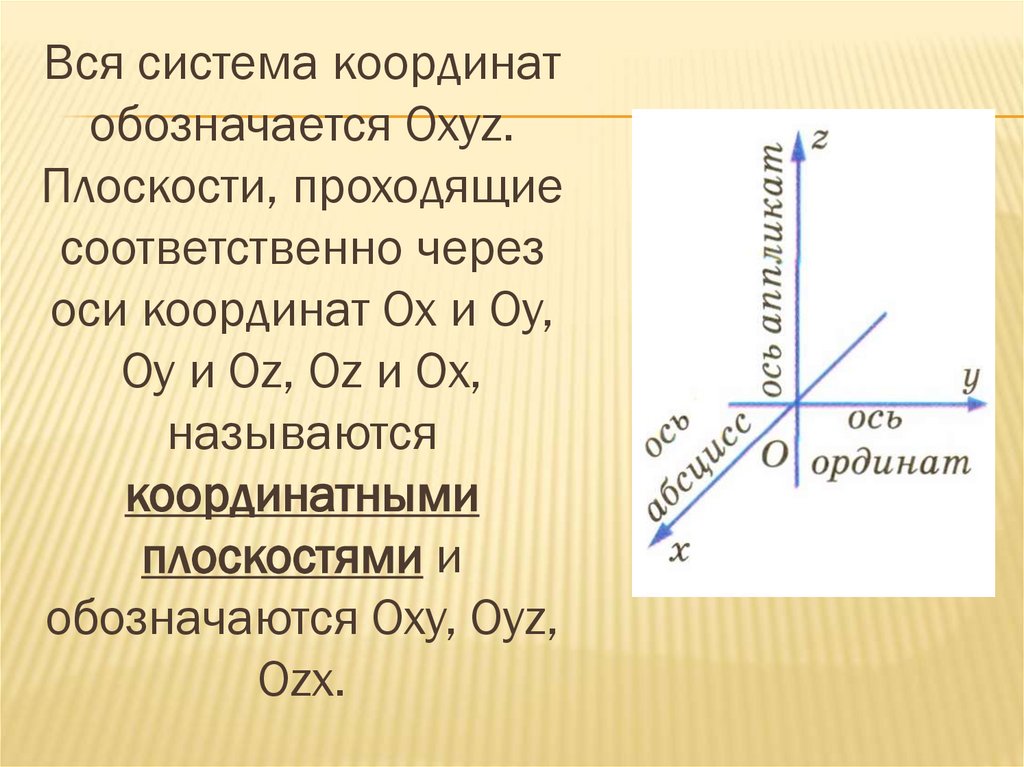
Вся система координат
обозначается Охуz.
Плоскости, проходящие
соответственно через
оси координат Ох и Оу,
Оу и Оz, Оz и Ох,
называются
координатными
плоскостями и
обозначаются Оху, Оуz,
Оzх.

5.

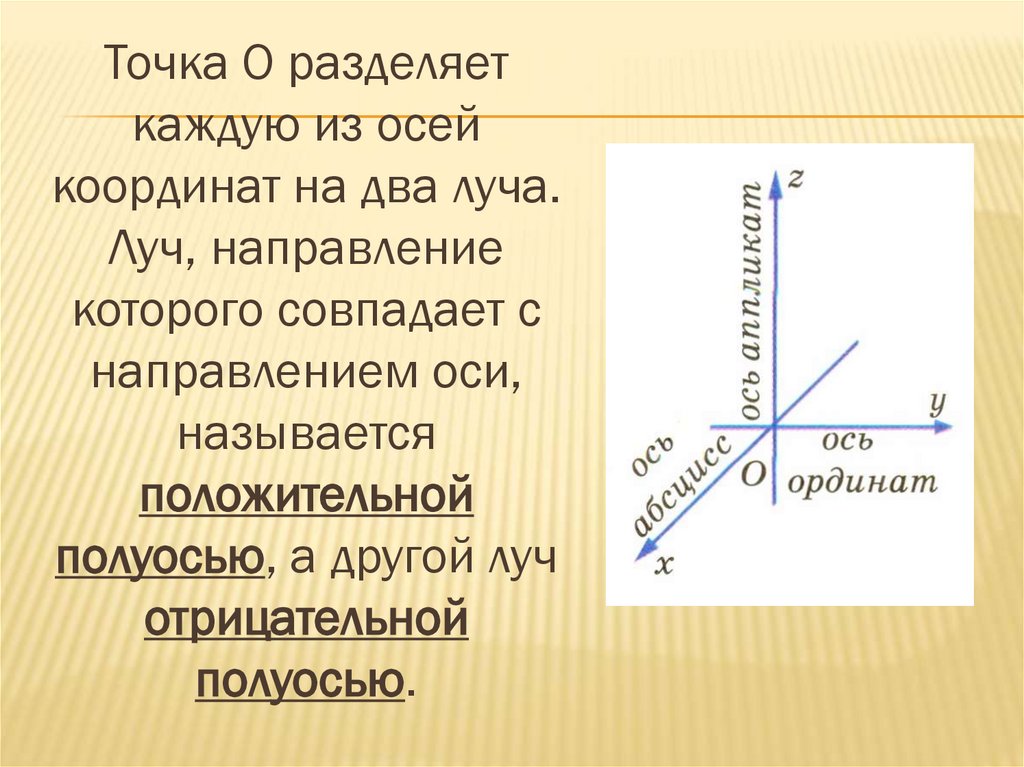
Точка О разделяет
каждую из осей
координат на два луча.
Луч, направление
которого совпадает с
направлением оси,
называется
положительной
полуосью, а другой луч
отрицательной
полуосью.

6.

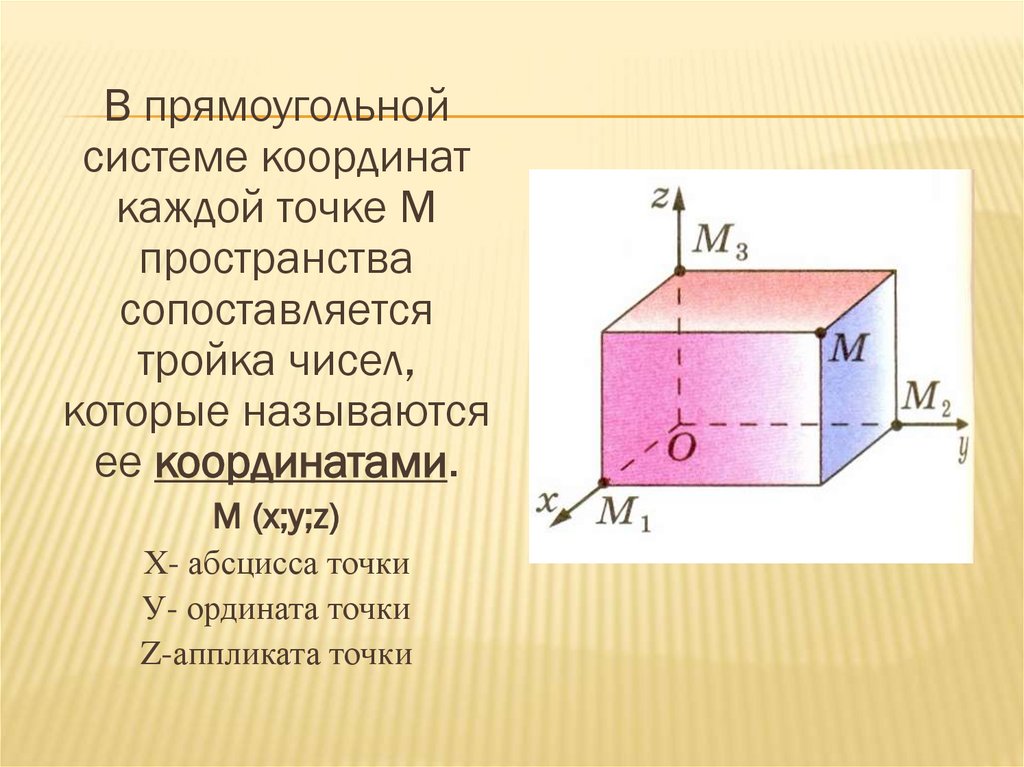
В прямоугольной
системе координат
каждой точке М
пространства
сопоставляется
тройка чисел,
которые называются
ее координатами.
М (х;у;z)
Х- абсцисса точки
У- ордината точки
Z-аппликата точки

7.

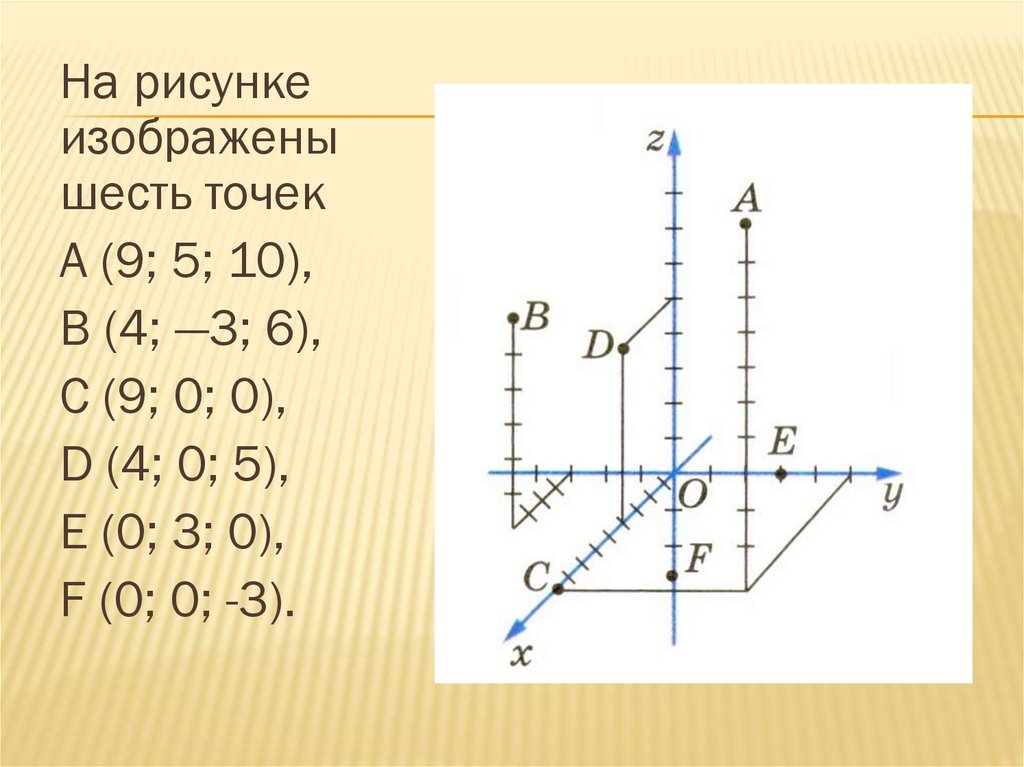
На рисунке
изображены
шесть точек
А (9; 5; 10),
В (4; —3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3).

8.

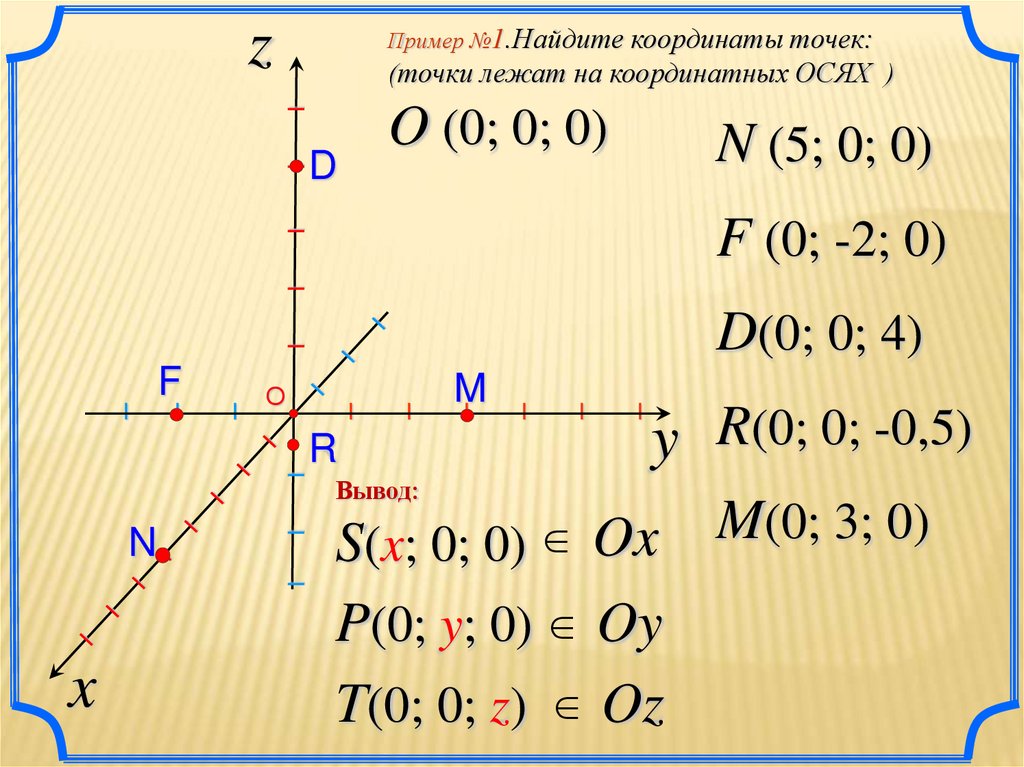
z
Пример №1.Найдите координаты точек:
(точки лежат на координатных ОСЯХ )
I
O (0; 0; 0)
N (5; 0; 0)
I
D
I
I
F (0; -2; 0)
I
D(0; 0; 4)
I
F
I
I
О
I
I
I
I
I
y R(0; 0; -0,5)
Вывод:
S(x; 0; 0) Ox
I
N
I
I
R
M
I
x
P(0; y; 0) Oy
T(0; 0; z) Oz
M(0; 3; 0)

9.

z
I
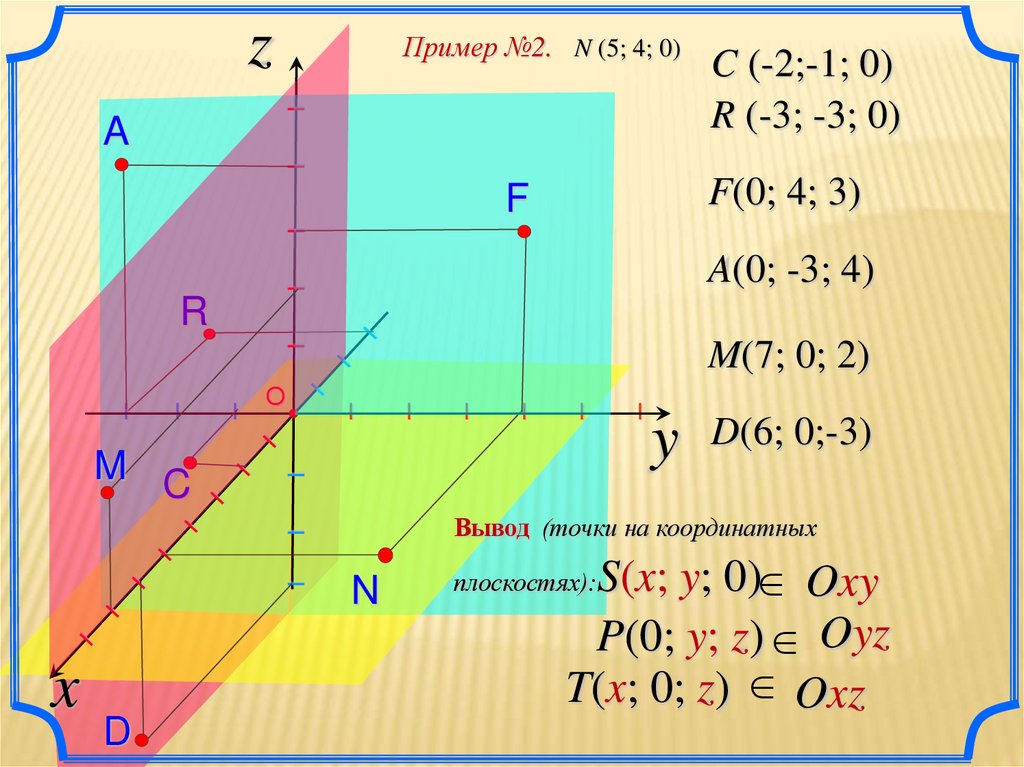
Пример №2. N (5; 4; 0)
I
A
C (-2;-1; 0)
R (-3; -3; 0)
F(0; 4; 3)
I
F
I
A(0; -3; 4)
R
I
M(7; 0; 2)
I
О
I
I
x
D
I
I
I
I
I
y D(6; 0;-3)
Вывод (точки на координатных
I
M C
I
I
I
N
S(x; y; 0) Oxy
P(0; y; z) Oyz
T(x; 0; z) Oxz
плоскостях):

10.

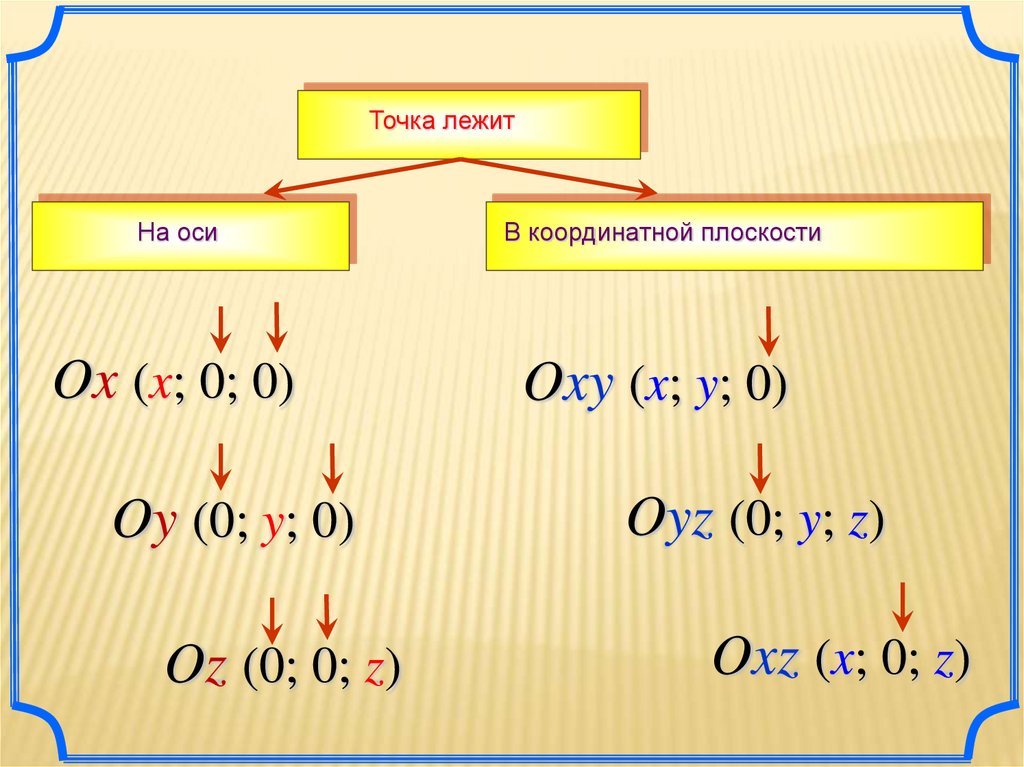
Точка лежит
На оси
В координатной плоскости
Ox (x; 0; 0)
Oxy (x; y; 0)
Oy (0; y; 0)
Oz (0; 0; z)
Oyz (0; y; z)
Oxz (x; 0; z)